1. На рисунке изображен график функции и отмечены точки 2, 1, 3, в какой из этих точек значение производной наибольшее В ответе укажите эту точку. 2
 Скачать 206.27 Kb.
|
|
1.  На рисунке изображен график функции  и отмечены точки −2, −1, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.2.  На рисунке изображён график функции  одной из первообразных некоторой функции  определённой на интервале  Пользуясь рисунком, определите количество решений уравнения  на отрезке  3.  На рисунке изображен график функции f(x) и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции f(x) в точке x0.4. Материальная точка движется прямолинейно по закону  (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 71 м/с?5. Материальная точка движется прямолинейно по закону  (г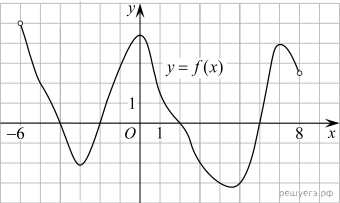де x —расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 3 с.6.  На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.7.  На рисунке изображён график функции и касательная к нему в точке с абсциссой  Найдите значение производной функции  в точке 8.  На рисунке изображён график некоторой функции (д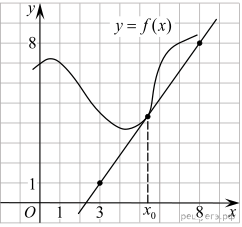ва луча с общей начальной точкой). Пользуясь рисунком, вычислите  где  — одна из первообразных функции  9.  На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке 10.  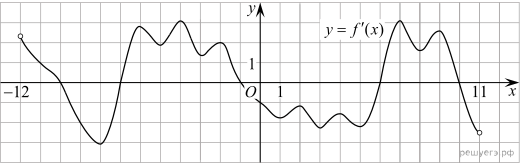На рисунке изображен график y = f '(x) — производной функции f(x), определенной на интервале (−12; 11). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−8; 9].11.  На рисунке изображён график некоторой функции  Функция  — одна из первообразных функции Найдите площадь закрашенной фигуры.12. Материальная точка движется прямолинейно по закону  (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  с.13.  На рисунке изображён график функции y = f(x), определённой на интервале (−8; 5). Найдите сумму точек экстремума функции f(x).14.  На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл  15. Прямая  является касательной к графику функции  Найдите с.16. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу   17. Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определён жребием. Всего в турнире участвует 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом? 18. При изготовлении подшипников диаметром 76 мм вероятность того, что диаметр будет отличаться от заданного не больше чем на 0,01 мм, равна 0,983. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 75,99 мм или больше чем 76,01 мм. 19. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трёх играх победила команда А. Какова вероятность того, что эта команда выиграет четвёртый раунд? 20. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 77% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным. 21. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых. 22. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля. 23. Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11». 24. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых. 25. В коробке 10 синих, 9 красных и 6 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер? 26. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка. 27. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»? 28. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86% случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? 29. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 14 октября погода в Волшебной стране хорошая. Найдите вероятность того, что 17 октября в Волшебной стране будет отличная погода. 30. В ящике четыре красных и два синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету? |