РАсчет редуктора вертолета. Детали машин редуктор вертолета. 1. Назначение редуктора 2 Задание 2
 Скачать 244.79 Kb. Скачать 244.79 Kb.
|
Оглавление1. Назначение редуктора 2 2. Задание 2 3. Исходные данные 2 4. Проектный расчет зубчатой передачи 3 5. Проверочный расчет конической передачи на контактную прочность 5 6.Проверочный расчет конической передачи на прочность по изгибу 6 7.Приближенное определение диаметров валов в самом нагруженном сечении 8 8.Выбор подшипников 8 9.Проверочный расчет валов 9 9.1 Работоспособность подшипников 10 9.2 Расчет опасных сечений 13 9.3 Расчет шлицевого соединения: 27 9.4 Расчет шпоночного соединения: 28 1. Назначение редуктораПромежуточный редуктор вертолета предназначен для передачи крутящего момента от главного к хвостовому редуктору, а от него на хвостовой винт вертолета. При этом промежуточный редуктор вертолета обеспечивает излом оси хвостового вала на заданный угол. Хвостовой винт применяют в конструкциях вертолетов с одним несущим винтом для компенсации реактивного момента. 2. Задание Входной вал Шестерня Колесо Выходной вал Фланец 3. Исходные данные
4. Проектный расчет зубчатой передачиВыбор материала зубчатых колес: Сталь 35: Твердость сердцевины (НВ): 350; Твердость поверхности (HRC): 52; Ϭв = 880 МПа; Ϭт = 635МПа; τТ = 360 МПа; Растяжение, Ϭ-1р = 312 МПа; Изгиб, Ϭ-1 = 390 МПа; Кручение, τ-1 =235 МПа; Ударная вязкость: 13 Дж/см2. Выбор относительной толщины зубчатого венца: ψ в R = 0.2 Выбор степени точности зацепления: При 2000 об/мин приблизительная окружная скорость будет равна 25 м/с при соблюдении габаритов, тем самым можно определить степень точности, которая будет равна 6. Выбор формы выполнения зуба: Так как приближенная окружная скорость равна 25 м/с, то зубья будут прямые. β=0. Определение чисел зубьев шестерни, колеса и передаточного числа: В первом приближении:  и Z2= и Z2=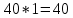 Кратность шестерен и колес соблюдена. Передаточное отношение U:  Отклонение передаточного числа есть равное 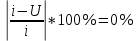 , что является меньше 2.5%. Следовательно количество зубьев на колесе и шестерне подобрано верно. , что является меньше 2.5%. Следовательно количество зубьев на колесе и шестерне подобрано верно.Определение предельных контактных напряжений в зубьях шестерни и колеса: При поверхностной закалке сталь 45 будет иметь следующие характеристики: ϬH lim a=2080 МПа ≥ ϬH lim 1≥ ϬH lim b=1084МПа 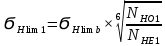  87739392 87739392 42000000 42000000 Так как неравенство считается выполненным, то можно принять: Ϭh lim 1= 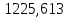 МПа и Ϭh lim min= МПа и Ϭh lim min=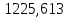 Мпа МпаПо таблице 1.7 определяем коэффициент безопасности Sн. Принимаем вероятность безотказной работы > 0.99, отсюда Sн = 1.3 Определение допускаемой величины контактных напряжений в зубьях передачи: 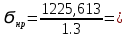 942,779 МПа 942,779 МПаОпределение значений коэффициентов KH α, KH β, KHV и функции f(β), входящих в формулу определения межосевого расстояния: K H α=1 по таблице 1.8; K H β=1 по таблице 1.9; K HV.=1 по первому приближению; f(β)=0,566. Номинальный вращающий момент 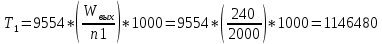 Определение конусного расстояния конической зубчатой передачи в первом приближении:  Определение модуля зацепления: 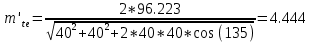 Ближайшее значение по первому ряду: mt e=5 Определение основных геометрических размеров зубчатой передачи: Делительные диаметры в наружном торцевом сечении: d1=5*40=200 мм и d2=5*40=200 мм; Конусное расстояние: 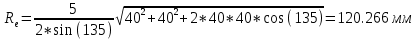 ; ;Рабочая ширина конических зубчатых венцов: bw=0.2*120.266=19.245 мм, округляем до ближайшего большего диаметра bw= b1= b2=25 мм; Среднее конусное расстояние: R m=  -0.5*25=88.766 мм; -0.5*25=88.766 мм;Половинные углы при вершинах делительных конусов:  , так как передаточное отношение равно 1, то оба колесо и шестерня должны быть абсолютно одинаковыми; , так как передаточное отношение равно 1, то оба колесо и шестерня должны быть абсолютно одинаковыми;δ2=135-67.5 = 67.5°; Наибольшая высота зубьев у торца: he=2*1*5+2=12 мм; Высота головок зубьев у торца: h a e= mt e=5 мм; 5. Проверочный расчет конической передачи на контактную прочностьОпределение коэффициентов ZH, ZM, Zε входящих в формулу для определения Ϭ H: ZH=1.76 ZM=270 Zε =1 Определение удельной расчетной окружной нагрузки на зубья при расчете контактной прочности:  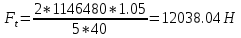  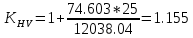 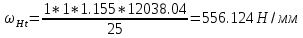 Определение расчетных контактных напряжений: 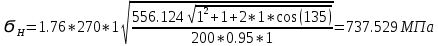 Проверка контактной прочности зубьев передачи: Ϭ Н=737.529 МПа≤942.779 МПа=Ϭ нр 6.Проверочный расчет конической передачи на прочность по изгибуϬ F1≤ Ϭ FP1 и Ϭ F2≤ Ϭ FP2 Определение расчетного местного напряжения у основания зуба шестерни и колеса Ϭ F 1,2: 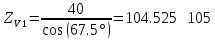  Коэффициент, учитывающий наклон линии зуба: Y β=1 Определение удельной расчетной окружной нагрузки на зубья при расчете на изгиб: εα=1.9; n=6; Коэффициент, учитывающий распределение нагрузки между зубьями при расчете на изгиб: 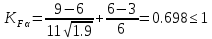 ; ;Коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатых венцов: K Fβ=1; Удельная окружная динамическая на зубья: 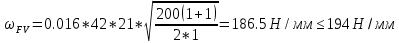 ; ;Удельная расчетная окружная нагрузка на зубья шестерни и колеса при расчете на изгиб:  . .Расчетные местные напряжения изгиба у основания прямых зубьев шестерни и колеса: Модуль в среднем нормальном сечении: 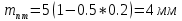  Определение предельных напряжений изгиба Ϭ -F lim в зубьях шестерни и колеса: 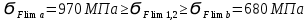   ϬF lim 1,2=523,653 МПа 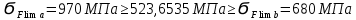 Коэффициент, учитывающий влияние шероховатости переходной поверхности у основания зуба на изгибную прочность: Y R=1 Коэффициент, учитывающий чувствительность материала зубьев к концентрации напряжений и масштабный эффект: 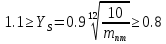 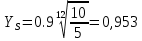 – условие неравенства выполнено – условие неравенства выполненоКоэффициент безопасности при расчете зубьев на изгиб: S F=2,2 Допускаемые напряжения изгиба в расчетных точках зубьев шестерни и колеса:  Проверка изгибной прочности зубьев шестерни и колеса конической передачи: Ϭ F 1.2=407,102 МПа≤ Ϭ FP 1,2=285,321 МПа Так как условие не соблюдается увеличиваем ширину венца на 38 мм, по стандартному первому ряду берем ширину bw = 63 мм. После повторения расчетов в пунктах 5 и 6 имеем: Ϭ F 1.2=203,104 МПа≤ Ϭ FP 1,2=285,321 МПа Условие выполнено. 7.Приближенное определение диаметров валов в самом нагруженном сеченииТ – вращающий момент, передаваемый валом, Н*мм: Т=1146480 Н*мм; К – коэффициент, учитывающий расположение зубчатых колес относительно подшипников: Квход=4,4 , Квых=4,4,; Ϭ -1=390 МПа. 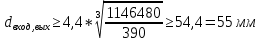 8.Выбор подшипниковДля редуктора, который имеет конические шестерню и колесо, а также консольное расположение зубчатой передачи относительно подшипников, были выбраны шариковые радиальные подшипники. Для входного вала:  d – номинальный диаметр отверстия внутреннего кольца; D – номинальный диаметр наружного кольца; B – номинальная ширина внутреннего кольца; T – номинальная монтажная ширина подшипника; β – угол контакта; C0 – статическая грузоподъемность; С – динамическая грузоподъемность.
9.Проверочный расчет валовТак как шестерня и колесо являются одинаковыми из-за передаточного отношения равного единице, то валы будут нагружаться одинаково, поэтому расчет проводится по одному валу. Расчет расстояния «а», которое определяет опору в подшипнике:  Определение нагрузок, действующих на вал: Окружная сила: 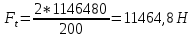 Радиальная сила: 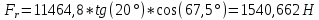 Осевая сила:  Определение опорной реакции Yб  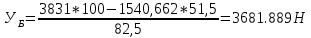 Определение опорной реакции Yа 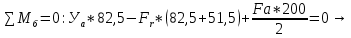 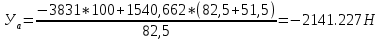 Проверка: Ya+Yб-Fr = 0; 3681.889-2141.227-1540.662 = 0, условие выполнено. Определение опорной реакции Zб:   Определение опорной реакции Za:  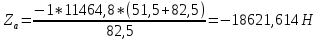 Проверка: Za+Zб+Fr=0; 7156.815-18621.614+11464.8 = 0, условие выполнено. Суммарные радиальные нагрузки на подшипники: 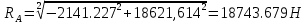 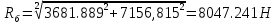 Определение осевых реакций в опорах: Осевая составляющая S: 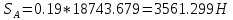 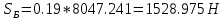 Условия правильной регулировки подшипников:   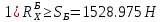 Так как SA 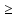 SБ, то SБ, то 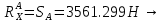 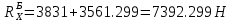 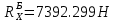 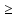 SБ= SБ= – неравенство выполняется – неравенство выполняется 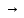 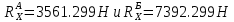 Перед продолжением произведем расчет долговечности подшипников для определения верности подбора подшипников. 9.1 Работоспособность подшипниковОпора А: Расчет эквивалентной нагрузки: X=0,56 – коэффициент осевой нагрузки; Y=2,3 – коэффициент радиальной нагрузки; V=1 – коэффициент кольца; Kб=1 – коэффициент безопасности; Kt=1,05 – температурный коэффициент; a=0.33– коэффициент понижения ресурса.  Определение долговечности подшипника: 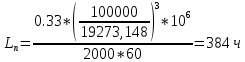  Опора Б: Расчет эквивалентной нагрузки: X=0.56 – коэффициент осевой нагрузки; Y=2,3 – коэффициент радиальной нагрузки; V=1 – коэффициент кольца; Kб=1 – коэффициент безопасности; Kt=1.05 – температурный коэффициент; a=0.33 – коэффициент понижения ресурса. 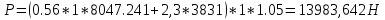 Определение долговечности подшипника: 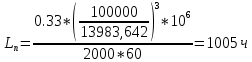  неравенство выполняется, но с большим запасом, возьмем меньшую серию ширин на опоре Б. неравенство выполняется, но с большим запасом, возьмем меньшую серию ширин на опоре Б.
Расчет расстояния «а», которое определяет опору в подшипнике:  Определение опорной реакции Yб 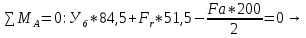  Определение опорной реакции Yа 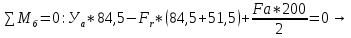 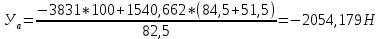 Проверка: Ya+Yб-Fr = 0;  - -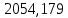 -1540.662 = 0, условие выполнено. -1540.662 = 0, условие выполнено.Определение опорной реакции Zб: 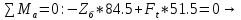  Определение опорной реакции Za: 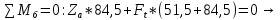 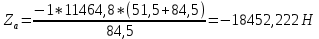 Проверка: Za+Zб+Fr=0; 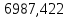 - -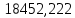 +11464.8 = 0, условие выполнено. +11464.8 = 0, условие выполнено.Суммарные радиальные нагрузки на подшипники: 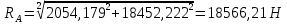  Опора А: Расчет эквивалентной нагрузки: X=0,56 – коэффициент осевой нагрузки; Y=2,3 – коэффициент радиальной нагрузки; V=1 – коэффициент кольца; Kб=1 – коэффициент безопасности; Kt=1,05 – температурный коэффициент; a=0.33– коэффициент понижения ресурса. 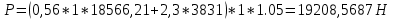 Определение долговечности подшипника: 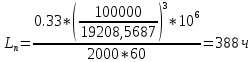 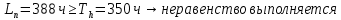 Опора Б: Расчет эквивалентной нагрузки: X=0.56 – коэффициент осевой нагрузки; Y=2,3 – коэффициент радиальной нагрузки; V=1 – коэффициент кольца; Kб=1 – коэффициент безопасности; Kt=1.05 – температурный коэффициент; a=0.33 – коэффициент понижения ресурса.  Определение долговечности подшипника: 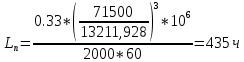 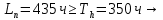 неравенство выполняется. неравенство выполняется.9.2 Расчет опасных сечений Определение напряжений в расчетных сечениях: Шпонка 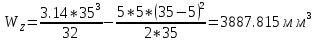 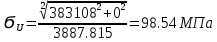  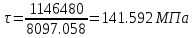  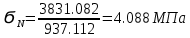 Нормальные напряжения изменяются по несимметричному циклу:  Предел выносливости материала по нормальным напряжениям: 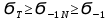 ϬТ=635 Мпа Ϭ-1=390 Мпа   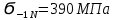 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ=2,01 – эффективный коэффициент концентрации напряжений; КdϬ=0.81 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 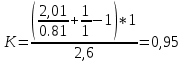 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений. Предел выносливости материала по касательным напряжениям: 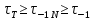 τТ=360 МПа τ-1=235 МПа  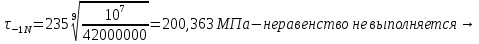 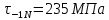 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=1,88 – эффективный коэффициент концентрации напряжений; Кdτ=0.81 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 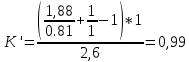 Запас прочности по нормальным напряжениям: 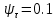 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.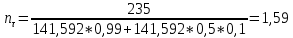 Результирующий запас прочности: 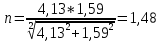 Галтель  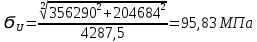  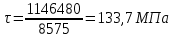  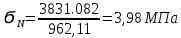 Нормальные напряжения изменяются по несимметричному циклу:  Предел выносливости материала по нормальным напряжениям: 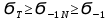 ϬТ=635 Мпа Ϭ-1=390 Мпа   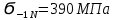 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ=2 – эффективный коэффициент концентрации напряжений; КdϬ=0.85 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 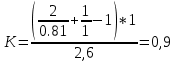 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений. Предел выносливости материала по касательным напряжениям: 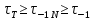 τТ=360 МПа τ-1=235 МПа  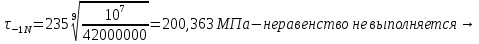 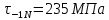 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=2 – эффективный коэффициент концентрации напряжений; Кdτ=0.73 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение.  Запас прочности по нормальным напряжениям: 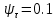 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.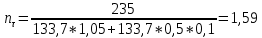 Результирующий запас прочности: 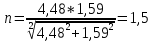 Изменение диаметра 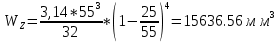   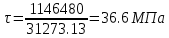 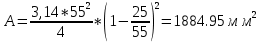  Нормальные напряжения изменяются по несимметричному циклу: 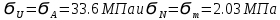 Предел выносливости материала по нормальным напряжениям: 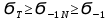 ϬТ=635 Мпа Ϭ-1=390 Мпа   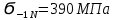 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ=2 – эффективный коэффициент концентрации напряжений; КdϬ=0.76 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 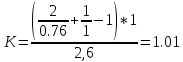 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.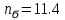 Предел выносливости материала по касательным напряжениям: 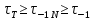 τТ=360 МПа τ-1=235 МПа  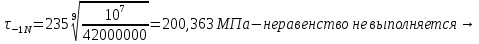 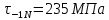 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=1 – эффективный коэффициент концентрации напряжений; Кdτ=0.65 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение.  Запас прочности по нормальным напряжениям: 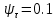 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.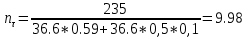 Результирующий запас прочности: 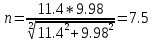 Опора А 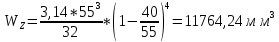  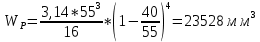 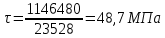 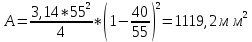  Нормальные напряжения изменяются по несимметричному циклу: 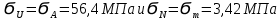 Предел выносливости материала по нормальным напряжениям: 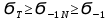 ϬТ=635 Мпа Ϭ-1=390 Мпа   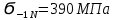 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ=1,67 – эффективный коэффициент концентрации напряжений; КdϬ=0.76 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1,67 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 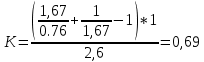 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.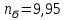 Предел выносливости материала по касательным напряжениям: 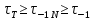 τТ=360 МПа τ-1=235 МПа  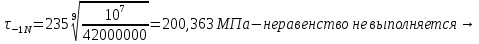 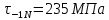 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=1,46 – эффективный коэффициент концентрации напряжений; Кdτ=0.76 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1,67 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение.  Запас прочности по нормальным напряжениям: 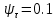 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.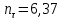 Результирующий запас прочности:  Опора Б  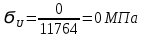 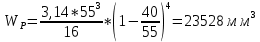 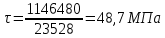 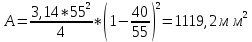  Нормальные напряжения изменяются по несимметричному циклу: 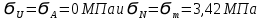 Предел выносливости материала по нормальным напряжениям: 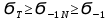 ϬТ=635 Мпа Ϭ-1=390 Мпа   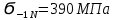 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ=1,76 – эффективный коэффициент концентрации напряжений; КdϬ=0.76 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1,67 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 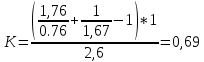 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений. Предел выносливости материала по касательным напряжениям: 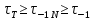 τТ=360 МПа τ-1=235 МПа  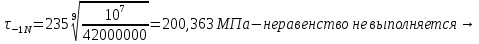 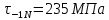 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=1,46 – эффективный коэффициент концентрации напряжений; Кdτ=0.65 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1,38 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 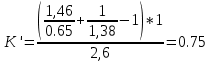 Запас прочности по нормальным напряжениям: 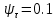 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.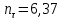 Результирующий запас прочности:  Изменение диаметра 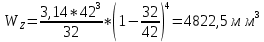 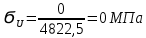 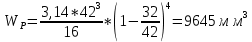  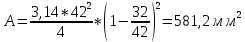 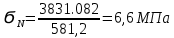 Нормальные напряжения изменяются по несимметричному циклу:  Предел выносливости материала по нормальным напряжениям: 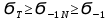 ϬТ=635 Мпа Ϭ-1=390 Мпа   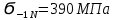 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ= 2 – эффективный коэффициент концентрации напряжений; КdϬ=0,85 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 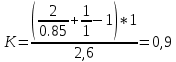 Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений. Предел выносливости материала по касательным напряжениям: 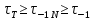 τТ=360 МПа τ-1=235 МПа  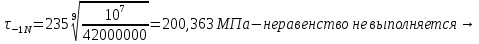 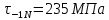 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=2 – эффективный коэффициент концентрации напряжений; Кdτ=0.73 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 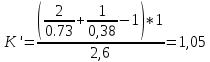 Запас прочности по нормальным напряжениям: 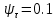 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.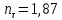 Результирующий запас прочности:  Шлицы  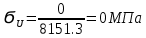 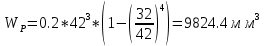 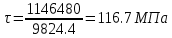  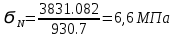 Нормальные напряжения изменяются по несимметричному циклу:  Предел выносливости материала по нормальным напряжениям: 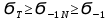 ϬТ=635 Мпа Ϭ-1=390 Мпа   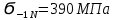 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: КϬ= 1.65 – эффективный коэффициент концентрации напряжений; КdϬ=0,85 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFϬ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение.  Запас прочности по нормальным напряжениям:  – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.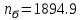 Предел выносливости материала по касательным напряжениям: 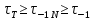 τТ=360 МПа τ-1=235 МПа  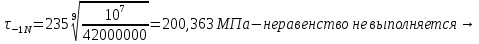 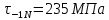 Расчет коэффициента снижения предела выносливости детали по нормальным напряжениям: Кτ=2.55 – эффективный коэффициент концентрации напряжений; Кdτ=0.73 – коэффициент, учитывающий влияние абсолютных размеров деталей; КFτ=1 – коэффициент, учитывающий влияние шероховатости; КV=2,6 – коэффициент, учитывающий поверхностное упрочнение. 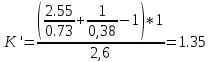 Запас прочности по нормальным напряжениям: 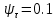 – коэффициент чувствительности материала к асимметрии цикла напряжений. – коэффициент чувствительности материала к асимметрии цикла напряжений.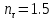 Результирующий запас прочности: 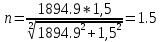 9.3 Расчет шлицевого соединения:T = 1146480 Н*мм – вращающий момент; h=5 мм; l= 22 мм – длина шлицов; z=10; ψ=0.65 – коэффициент, учитывающий неравномерное распределение нагрузки между зубьями; dm= 47 мм – средний диаметр шлицев.  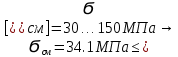  9.4 Расчет шпоночного соединения:T = 1146480 Н*мм – вращающий момент; dm= 35 мм – диаметр вала; l= 22 мм – рабочая длина шпонки; t = 4 мм - глубина врезания шпонки в ступицу; ψ=0.75 – коэффициент, учитывающий неравномерное распределение нагрузки между зубьями. 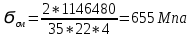 Возьмем шпонку из стали 12Х2Н4А 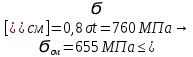 неравенство удовлетворено. неравенство удовлетворено. |
