1. Організація та планування дослідження. Мета та завдання дослідження
 Скачать 68.24 Kb. Скачать 68.24 Kb.
|
|
1. Організація та планування дослідження. Мета та завдання дослідження. 1-й етап: формування гіпотези складання плану та програми статистичного дослідження 2-й етап: статистична реєстрація (збирання матеріалу) 3-й етап: розробка і зведення даних 4-й етап: аналіз статистичних матеріалів 5-й етап: упровадження результатів дослідження Мета будь-якого наукового дослідження - розкриття суті масових явищ, процесів, закономірностей. 2. Об‘єкт, одиниця спостереження, облікові ознаки. Види групувань. Об'єкт статистичного спостереження повинен мати межі визначеної для вивчення сукупності. Одиниця спостереження (одиниця обліку) - це складова частина статистичної сукупності (особа, явище), ознаки якої підлягають реєстрації та вивченню. Кожна одиниця спостереження має багато характеристик, проте враховуються тільки ті з них, які необхідні для досягнення поставленої мети і рішення конкретних задач, дослідження. Ці ознаки враховують (реєструють) і тому їх називають обліковими. Облікові ознаки поділяються: на атрибутивні (описові), виражені словесно, кількісні (виражені числом). Види групувань: 1) типологічне (атрибутивне - описові, якісні ознаки) – стать, діагноз тощо; 2) варіаційне (кількість ознаки) – вік, зріст тощо 3. Джерела статистичної інформації. Облікові та звітні форми. офіційні звітно-обліков спеціально розроблені облікові документи. методи обліку: безпосередня реєстрація; документальний облік; копіювання; опитування; анкетування. Програма розробки (зведення) - складання макетів таблиць. Зведення проводиться у вигляді статистичних таблиць, які заповнюються за даними зведених статистичних матеріалів 4. Методи збирання статистичного матеріалу. методи обліку: безпосередня реєстрація; документальний облік; копіювання; опитування; анкетування. 5. Класифікація статистичних досліджень за часом. Сринінг. Проспективні та ретроспективні дослідження. за часом: поточні, періодичні та одночасні. Скринінг – масове обстеження осіб, що не вважають себе хворими, для виявлення захворювань з прихованим перебігом або інших станів (факторів ризику можливих захворювань). Проспективні дослідження зазвичай мають менше потенційних джерел упередженості та викривлення їх висновків, ніж ретроспективні дослідження. З іншого боку, ретроспективне дослідження дивиться у минуле та вивчає вплив на потенційних факторів ризику або захисту стосовно результату, встановленого на початку дослідження. 6. Класифікація статистичних досліджень за обсягом. Вибіркове спостереження як джерело статистичної інформації. суцільні несуцільні (часткові). Суцільне дослідження охоплює всі одиниці спостереження, які входять до складу сукупності, що вивчається (генеральна сукупність). Несуцільне дослідження може бути монографічним, основного масиву, вибірковим. Вибірковим називається дослідження, при якому характеристика всієї сукупності фактів дається за деякою її частиною, яка відібрана випадковим шляхом, чи за певними критеріями. 7. Абсолютні дані, відносні величини, особливості використання. статистиці абсолютні дані використовуються для характеристики чисельності населення, кількості лікувально-профілактичних закладів, ліжкового фонду, кадрового потенціалу та інші Відносні величини – це показники, які відображають кількісні співвідношення двох величин. Важливою умовою правильного застосування відносних величин є порівнянність показників, які використовуються для їх обчислення, за періодами часу, територією, охопленням одиниць сукупності, одиницями вимірювання, способами обміну тощо. 8. Середні величини в клінічних та епідеміологічних дослідженнях, їх види, практичне значення, методи розрахунку. Середні величини – є узагальнюючими мірами кількісних ознак у сукупності, вони широко використовуються для оцінки стану здоров’я населення, діяльності лікувально-профілактичних закладів. У статистичній практиці використовують декілька видів середніх: - середня арифметична; - середня гармонічна; - середня квадратична; - середня геометрична. Середня арифметична — одна з найбільш поширених видів середньої, застосовується у тих випадках, коли обсяг варіюючої ознаки для всієї сукупності є сумою індивідуальних значень її окремих елементів. Середня арифметична використовується для осереднення прямих значень ознаки шляхом їх підсумування. Логічна формула має вигляд: 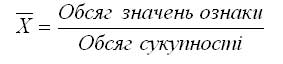 Якщо дані не згруповані, використовується середня арифметична проста.  Якщо дані згруповані, то використовують середньозважену арифметичну: 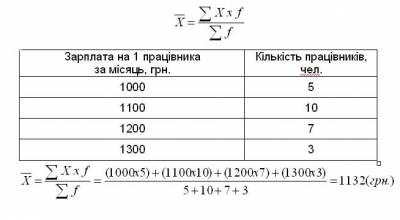 Середня гармонійна застосовується у тих випадках, коли нам відомі не самі вартості, а їхні обернені числа. Середня гармонійна використовується для осереднення індивідуальних значень ознаки шляхом їх підсумування. Для не згрупованих даних - це середня гармонійна проста: 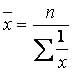 Якщо дані згруповані, то використовують середню гармонійну зважену: 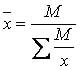 де М — обсяг значень ознаки, тобто Середню гармонійну зважену доцільно використовувати, коли відсутня інформація про значення знаменника логічної формули, тобто відсутні ваги. Середню гармонійну використовують тоді, коли вагою слугують не одиниці сукупності (носії ознаки), а добуток цих одиниць на значення ознаки, Використання кожного виду середніх залежить від двох обставин: • по-перше, від характеру індивідуальних значень ознаки; • по-друге, від характеру алгебраїчного зв'язку між індивідуальними значеннями ознаки та її загальним обсягом. У статистиці для обчислення середніх постає питання вибору виду середньої у кожному конкретному випадку дослідження. 9. Методи оцінки мінливості параметрів сукупності. Середнє квадратичне відхилення, коефіцієнт варіації. Середні величини як узагальнені показники характеризують сукупність за варіаційною ознакою, вказують на їх типовий рівень у розрахунку на одиницю однорідної сукупності. У статистиці під варіацією розуміють кількісні зміни ознаки в межах однорідної сукупності. Середнє квадратичне відхилення буває просте і зважене. 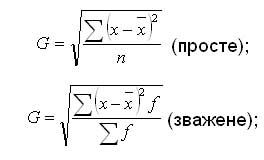 Середнє квадратичне відхилення є абсолютним виміром варіації, це означає, що порівнювати їх у варіаційних рядах різних явищ не можна. Змістовне значення показує, на скільки в середньому відхиляються індивідуальні значення варіант від їх середнього значення. Середнє квадратичне відхилення є критерієм надійності середньої. Чим воно менше, тим краще середня арифметична відображає всю досліджувану сукупність. Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень відхилень окремих варіант від середньої арифметичної. 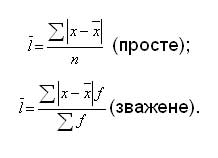 Прямі дужки означають, що абсолютні значення відхилень беруться по модулю, тобто підсумовування виконується без врахування знаків (плюс або мінус). Така умовність пояснюється тим, що оскільки сума відхилень індивідуальних значень ознаки від середньої в першому ступені дорівнює нулю (нульова властивість середньої арифметичної),то для одержання суми всіх відхилень, відмінної від нуля, кожне відхилення слід брати як додатну величину. 10. Метод стандартизації, характеристика, оцінка результатів. Статистичний метод, за допомогою якого можна виключити вплив неоднорідності складу порівнюваних груп на досліджувані загальні показники, називають методом стандартизації. Його застосування дозволяє розрахувати стандартизовані (умовні ) показники, які могли мати місце за умови однакового складу населення в порівнюваних групах. Практична значимість методу стандартизації полягає в можливості по рівняння частоти однотипних явищ у неоднорідних групах та оцінці впливу до сліджуваного фактора на величину загальних показників. Існує три методи стандартизації: прямий, використовують при наявності даних про склад населення та склад досліджуваного явища за певними параметрами (віком, професіями, термінами госпіталізації, тяжкістю захворювання і т.д.). опосередкований Відсутність даних про розподіл певного явища, або незначна чисельність груп при даному розподілі, що знижує вірогідність погрупових показників, є умовами для використання опосередкованого методу зворотний. Відсутність даних про склад населення обумовлює необхідність використання зворотного методу. Етапи розрахунків: І етап - розрахунок погрупових та загальних інтенсивних показників. II етап - вибір та розрахунок стандарту. III етап - розрахунок “очікуваного” числа хворих за стандартом. IV етап - обчислення стандартизованих показників. 11. Середня похибка середньої та відносної величини, довірчий інтервал. Ймовірність влучення середньої або відносної величини в довірчий інтервал називаєтьсядовірчою ймовірністю. довірчі кордонусередньої арифметичної генеральної сукупностівизначають за формулою: Мген= Мвиб± t · mM Довірчі межі відносної величини в генеральній сукупності визначають за такою формулою: Рген= Рвиб ± t · mр Де: Мгені Рген- Значення середньої і відносної величин, отриманих для генеральної сукупності; Мвибі Рвиб- Значення середньої і відносної величин, отриманих для вибіркової сукупності; mMі mр- Помилки репрезентативності вибіркових величин; t - довірчий критерій, який залежить від величини безпомилкового прогнозу, що встановлюється при плануванні дослідження. твірt · m(?)- Гранична помилка показника, отриманого при даному вибірковому дослідженні. Розміри граничної помилки залежать від коефіцієнтаt, Який обирає сам дослідник, виходячи із заданої ймовірності безпомилкового прогнозу. величина критеріюtпов'язана з ймовірністю безпомилкового прогнозу(Р)і числом спостережень в вибіркової сукупності Для більшості медико-біологічних і соціальних досліджень достовірними вважаються довірчі межі, встановлені з ймовірністю безпомилкового прогнозу = 95% і більше. Щоб знайти критерій t при числі спостережень (n) <30, необхідно користуватися спеціальною таблицею Н. А. Плохинський (табл. 4.2), в якій зліва показано число спостережень - одиниця (n - 1), а зверху (Р) - ступінь ймовірності безпомилкового прогнозу. При визначенні довірчих кордонів спочатку треба вирішити питання про те, з яким ступенем ймовірності безпомилкового прогнозу необхідно представити довірчі кордону середньої або відносної величини. Обравши певний ступінь ймовірності, відповідно до цього знаходять величину довірчого критерію t при даному числі спостережень. Таким чином, довірчий критерій встановлюється заздалегідь, при плануванні дослідження. Будь-параметр (середня або відносна величина) може оцінюватися з урахуванням довірчих меж, отриманих при розрахунку. наприклад:потрібно визначити довірчі межі середнього рівня пепсину у хворих гіпертеріоза з 95% ймовірністю безпомилкового прогнозу. Якщо відомо, що: n = 49; Мвиб= 1г%; mм= ± 0,05 г% 1. Визначення довірчих меж середньої величини в генеральній сукупності: Мген= Мвиб± t · mM= 1г% ± 2·0,05г% 1г% + 0,1г% = 1,1 г% Мген = 1г% - 0,1г% = 0,9 г% висновок: Встановлено з ймовірністю безпомилкового прогнозу 95%, що середній рівень пепсину в генеральної сукупності у хворих гіпертеріоза знаходиться в межах від 1,1 г% до 0,9 г%. Як видно, довірчі кордону залежать від розміру довірчого інтервалу. Аналіз довірчих інтервалів вказує, що при заданих ступенях імовірності і n> 30 - t має незмінну величину і при цьому довірчий інтервал залежить від величини помилки репрезентативності. Зі зменшенням величини помилки звужуються довірчі кордону середніх і відносних величин, отриманих на вибіркової сукупності, т. Е уточнюються результати дослідження, які наближаються до відповідних величинам генеральної сукупності. Якщо помилка велика, то отримують для вибіркової величини великі довірчі кордону, які можуть суперечити логічної оцінки шуканої величини в генеральній сукупності. У подібному випадку треба шукати резерви скорочення розмаху довірчих меж в розмірі величини помилки репрезентативності. довірчі кордону Мвиб и Рвиб залежать не тільки від середніх помилок цих величин, але і від обраної дослідником ступеня ймовірності безпомилкового прогнозу. При великій мірі ймовірності розмах довірчих меж збільшується. 12. Оцінка вірогідності різниці: критерій Ст‘юдента, методика розрахунку, його оцінка У медицині та охороні здоров'я по різниці параметрів оцінюють середні і відносні величини, отримані для різних груп населення за статтю, віком, а також груп хворих і здорових і т. Д. У всіх випадках при зіставленні двох порівнюваних величин виникає необхідність не тільки визначити їх різницю, але і оцінити її достовірність. Достовірність різниці величин, отриманих при вибіркових дослідженнях, означає, що висновок про їх відмінності може бути перенесений на відповідні генеральні сукупності. Достовірність різниці вибіркової сукупності вимірюється довірчим критерієм, який розраховується за спеціальними формулами для середніх і відносних величин. Формула оцінки достовірності різниці порівнюваних середніх величин: M1- M2 t = --- m12+ m22 Для відносних величин: Р1- Р2 t = --- m12+ m22 де: M1; M2; Р1; Р2- Параметри, отримані при вибіркових дослідженнях; m1; m2 - Їх середні помилки; t - Критерій достовірності (Ст'юдента). Різниця статистично достовірна при t ? 2, що відповідає ймовірності безпомилкового прогнозу, що дорівнює 95% і більше. Для більшості досліджень, що проводяться в медицині і охороні здоров'я, такий ступінь ймовірності є цілком достатньою. При величині критерію достовірності t <2 ступінь ймовірності безпомилкового прогнозу становить Р <95%. При такому ступені ймовірності можна стверджувати, що отримана різниця показників достовірна з достатнім ступенем вірогідності. В цьому випадку необхідно отримати додаткові дані, збільшивши число спостережень. Іноді при збільшенні чисельності вибірки різниця продовжує залишатися не достовірною. Якщо при повторних дослідженнях різниця залишається недостовірної, можна вважати доведеним, що між порівнюваними сумами не виявлено відмінностей по досліджуваному ознакою. наприклад: потрібно визначити, чи достовірні відмінності в рівні пепсину в шлунковому соку хворих гіпертеріоза і здорових осіб. Обстежуються на пепсин дві групи: 49 хворих гіпертеріоза і 50 здорових людей (контрольна група). M1- M2 t = --- m12+ m22 висновок: при гіпертеріоза спостерігається зниження рівня пепсину, що підтверджується з великим ступенем ймовірності безпомилкового прогнозу (Р 99,9%). Отже, зниження рівня пепсину може бути використано в якості одного із симптомів для підтвердження діагностики гіпертеріоза. Подібним же чином оцінюють достовірність різниці порівнюваних відносних величин. Зазначена методика оцінки достовірності і різниці результатів дослідження дозволяє проводити тільки порівняння груп по парам, при обов'язковій наявності узагальнюючих параметрів - середніх арифметичних або відносних величин та їх середніх помилок. 13. Вивчення зв‘язку між кількісними перемінними. Кореляція, види коефіцієнтів кореляції. Оцінка коефіцієнту кореляції. Існують дві форми кількісних зв'язків між явищами і процесами, це функціональні і кореляційні зв’язки. Під функціональним зв'язком розуміють такий зв'язок, коли будь якому значенню однієї ознаки відповідає конкретне значення іншої взаємопов'язаної з ним ознаки, радіус кола відповідає певній площі. Під кореляційним зв'язком розуміють зв'язок, коли середньому значенню однієї ознаки, відповідає кілька значень іншої взаємопов'язаної з ним ознаки (середньому зростанню статистичної сукупності відповідає кілька значень маси одиниць спостережень). У медичних, соціальних, біологічних дослідженнях найчастіше спостерігається саме кореляційна залежність, в зв'язку з чим більш детально охарактеризуємо її. Необхідно пам'ятати, що кореляційні зв’язки проявляються тільки в якісно однорідній статистичній сукупності. Кореляційний зв'язок можна представити у вигляді: – таблиць; – графіка; – коефіцієнта кореляції. Недолік таблиць і графіків в тому, що вони дають уявлення про наявність зв'язку і його напрямок, але не характеризують його силу, яка є найважливішою характеристикою для формулювання висновків дослідження. Коефіцієнт кореляції (Rxy) одним числом визначає наявність зв'язку, його напрямок та силу залежності ознак між собою, в цьому і полягає перевага коефіцієнта кореляції перед таблицями і графіками. Під силою кореляційного зв'язку розуміють ступінь пов'язаності між ознаками або ступінь залежності однієї ознаки від іншої. Сила кореляційної зв'язку знаходиться в межах від 0 до ±1 і її рівень оцінюється за спеціальною приведеною нижче шкалою: 0 – зв'язок відсутній; від ±0,1 до ± 0,29 – слабка залежність; від ±0,3 до ± 0,69 – середня залежність; від ±0,7 до ±0,99 – сильна залежність; ± 1 – повна залежність. За напрямком кореляційний зв'язок може бути: – прямий; – зворотній. При прямому кореляційному зв'язку, зі зміною значення однієї ознаки змінюється значення іншої ознаки, яка була взаємопов'язана з нею в тому ж напрямку (наприклад, з підвищенням температури тіла у людини збільшується частота пульсу). Позначається прямий зв'язок знаком (+). При зворотному кореляційному зв'язку зі зміною значення однієї ознаки змінюється значення іншої ознаки, яка була взаємопов'язана з нею в зворотному напрямку (наприклад, восени, чим нижче температура навколишнього середовища, тим вище захворюваність серед дитячого населення. Зворотній зв'язок позначається знаком (–). Крім того, кореляційний зв'язок може бути: − прямолінійним; − криволінійним. Прямолінійний зв'язок характеризується відносно рівномірною зміною значень однієї ознаки, при рівній зміні іншої ознаки (наприклад, при вимірюванні артеріального тиску відповідність між максимальним і мінімальним рівнями АТ). При криволінійному кореляційному зв’язку інше співвідношення: при рівномірній зміні значення однієї ознаки можуть спостерігатися зростаючі або спадаючі значення іншої ознаки. Вимірювання і оцінка зв'язку між явищами при прямолінійному кореляційному зв’язку здійснюється за допомогою коефіцієнта кореляції, а при криволінійному зв’язку – кореляційним відношенням 14. Поняття про когортні дослідження, дослідження «випадок-контроль», клінічні випробування. Дослідження випадок-контроль (case control study) – аналітичне ретроспективне дослідження, метою якого є виявлення факторів ризику хвороби, що досліджується. Основну групу відбирають з хворих на хворобу, що досліджують, контрольну групу складають здорові особи. Факт впливу досліджуваних факторів ризику визначається, опитуванням осіб порівнюваних груп, їх родичів, за архівними даними. Порівняння частоти виникнення окремих факторів в основній та контрольній групі дозволяє розрахувати показник відношення шансів (OR), за величиною якого, орієнтовно оцінюється наявність причинно-наслідкового зв'язку. Когортне дослідження(cohort study) – аналітичне дослідження, в якому термін «когорта» (cohorta) означає групу осіб, що об’єднані будь-якою спільною ознакою та за якими спостерігають протягом певного періоду часу, щоб встановити, що з ними відбудеться в подальшому. При проведенні дослідження, в когорту включаються особи, у яких захворювання, що досліджують – відсутнє, але може проявитися в подальшому. Наприклад, при дослідженні фактора ризику виразкової хвороби шлунка всі включені в когорту особи не повинні страждати хворобами шлунка. Когортне дослідження дозволяє оцінити відносний ризик (RR) виникнення (розповсюдження) хвороби, пов'язаний з передбачуваними факторами ризику. Когортні дослідження – найкраща заміна істинного експерименту в ситуації, коли експеримент неможливий. Когортне (followup) дослідження проводиться як проспективне. Недоліком когортного методу є: – число осіб, включених в дослідження, повинно бути значно більше, ніж число пацієнтів з досліджуваним захворюванням, в зв'язку з чим цей метод непридатний для рідкісних захворювань; – висока вартість дослідження за рахунок того, що необхідно тривалий час обстежувати велику кількість людей; – результати довгий час залишаються невідомими; – дозволяє оцінити зв'язок між захворюванням і впливом відносно невеликого числа факторів (тих, які були визначені на початку дослідження). Дослідження «випадок-контроль» та когортне дослідження – це альтернативні методи при оцінці факторів ризику. 15. Шляхи впровадження результатів досліджень в практику. Впровадження – це передача замовнику НДР наукової продукції (результатів досліджень, методик, інструкцій, звіту) у зручній для реалізації формі, що забезпечує техніко-економічний ефект. Необхідно зауважити, що НДР перетворюється у реальний продукт лише з моменту споживання науково-дослідної роботи замовником. Отже, впровадження завершених наукових досліджень полягає у передачі їх у практичне використання. Основними результатами наукових досліджень є такі: - підтвердження теоретичних закономірностей результатами експерименту; - розробка нових методів та методик, які використовувались в дослідженні; - застосування розроблених методів, методик, алгоритмів та ін. в процесі обміну, контролю, аналізу, оцінки, організації управління галуззю, підприємством, тощо; - застосування результатів досліджень в навчальному процесі. Як би ретельно не проводились НДР у науково-дослідних організаціях, вони е можуть враховувати всі фактори, які діють в умовах виробництва. Тому впровадження у виробництво на першій стадії потребує додаткової перевірки результатів дослідження у виробничих умовах. Після дослідно-виробничого випробування розроблені нові матеріали, конструкції, технології, методики впроваджують у серійне виробництво як елементи нової техніки. Впровадження результатів НДР фінансують організації, які його здійснюють. |
