шпорки по физике-1. 1. основные харки мех. Движения. Прямолинейное и криволинейное движение материал. Точки. Скорость и ускорение. Механика

• Название: 1. основные харки мех. Движения. Прямолинейное и криволинейное движение материал. Точки. Скорость и ускорение. Механика
• Дата: 21.05.2022
• Размер: 2.4 Mb.
• Имя файла: шпорки по физике-1.doc
• Тип: Документы; #542230
• страница: 5 из 14

14.ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ.РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ ПРОЦЕССЫ. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ.

Системой называется конечная область пространства с находящимися в ней физическими объектами исследования. Граница системы может быть материальной или воображаемой, неподвижной или движущейся, проницаемой или непроницаемой для вещества.

Мы будем изучать свойства макроскопических систем, т.е. систем, состоящих из огромного числа частиц – молекул, атомов или ионов. Такой макроскопической системой может быть отдельное тело (например, газ, жидкость и находящийся в равновесии с ней пар). Все тела, не входящие в рассматриваемую систему, но могущие влиять на ее свойства называются средой. Если, например, системой является газ, заключенный в цилиндр с поршнем, то цилиндр и поршень в систему не входят, но свойства системы, в частности ее объем, зависят от положения поршня. Поэтому в данном случае цилиндр и поршень относятся к среде.

Для описания поведения и свойств макроскопических систем обычно пользуются непосредственно измеряемыми величинами, которые характеризуют систему в целом и ее отношение к окружающей среде, но не имеют смысла в применении к отдельным частицам. К числу таких величин, называемых макроскопическими параметрами состояния системы, относятся, например, такие величины, как Р, Т, V,  и т.п. Состояние системы, заданное с помощью макропараметров, характеризующих поведение системы в целом, называется макросостоянием.

Опыт показывает, что всякая макроскопическая система, изолированная от внешней среды, всегда самопроизвольно переходит в состояние так называемого термодинамического равновесия, которое характеризуется тем, что всякие макроскопические изменения в системе прекращаются и каждый параметр, характеризующий то или иное макроскопическое свойство системы, имеет постоянное во времени значение. Система, перешедшая в состояние термодинамического равновесия, самопроизвольно никогда из него не может выйти. Для нарушения равновесия необходимы внешние воздействия. Процесс перехода системы в состояние термодинамического равновесия называется релаксацией, а время, потребное на это, называется временем релаксации. Для разных процессов в разных системах время релаксации различно. Оно может быть очень малым и очень большим. Например, выравнивание давления в газе происходит за доли секунды, а выравнивание концентрации при диффузии может длиться минуты в газах, а в твердых телах – часы, недели и даже годы.

Термодинамическое равновесие есть равновесие статистическое. О нем можно говорить только в случае, когда число частиц, составляющих систему, очень велико. Параметры состояния системы при равновесии, строго говоря, не остаются постоянными, а испытывают небольшие колебания около своих равновесных значений. Например, при большом числе молекул некоторые отклонения от равномерного распределения их по объему могут иметь место в отдельных частях сосуда. Однако, средняя плотность газа во всем объеме будет одинакова и постоянна.

Состояние термодинамического равновесия является наиболее простым состоянием макроскопической системы. В этом состоянии поведение системы описывается небольшим числом макроскопических параметров. Например, состояние простейших систем – газов, жидкостей и твердых тел при отсутствии внешних силовых полей может быть в условии термодинамического равновесия однозначно определено какими-либо двумя из трех величин Р, Т, V, которые при отсутствии внешних полей имеют одинаковые значения во всех частях системы. Каждое такое равновесное состояние может быть изображено точкой на графике Р-V или Т-V. Неравновесное состояние не может быть изображено подобным способом, потому что хотя бы один из параметров в неравновесном состоянии не будет иметь определенного значения.

Всякий процесс, т.е. переход системы из одного состояния в другое, связан с нарушением равновесия в системе. При этом нарушение равновесия тем значительнее, чем быстрее происходит процесс. Пример: изменение Р при быстром и медленном сжатии газа в цилиндре с плотно пригнанным поршнем.

В пределе, если сжатие газа происходит бесконечно медленно, газ в каждый момент времени будет характеризоваться определенными значениями давления. Следовательно, в этом случае состояние газа в каждый момент времени является равновесным, и бесконечно медленный процесс будет состоять из последовательности равновесных состояний. Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным или квазистатическим процессом. Из сказанного выше следует, что равновесным может быть только достаточно медленный процесс, поэтому равновесный процесс является абстракцией. Практически близкими к равновесным являются такие процессы, при которых скорость изменения параметров системы гораздо меньше скорости изменения тех же параметров при релаксации. Равновесный процесс может быть изображен на графике Р-V или Т- V соответственной кривой. Неравновесный процесс не может быть изображен графически. Если все же применить для неравновесных процессов графическое изображение, то это имеет только тот смысл, что показывает относительный ход этих процессов по сравнению с равновесными.

Все количественные выводы термодинамики строго применимы только к равновесным процессам.

Равновесные процессы в отличие от неравновесных обладают одной важной особенностью: они являются процессами обратимыми, в то время как неравновесные процессы всегда необратимы.

Обратимым процессом называется такой процесс, который может быть проведен в обратном направлениитак, чтобы система прошла черезте же промежуточные состояния, что и в прямом направлении, но в обратной последовательности, и чтобы при этом в окружающей систему среде не произошло никаких изменений.

Если же процесс протекает таким образом, что после его окончания систему нельзя вернуть в начальное состояние так, чтобы она проходила через те же промежуточные состояния, но только в обратном порядке, и чтобы при этом нигде в среде не осталось никаких изменений, то процесс называется необратимым.

Обратимый процесс в отличие от необратимого обладает следующим свойством: если при прямом ходе на каком-то элементарном участке процесса система получает тепло Q и совершает работу dА, то при обратном ходе на том же участке система отдает тепло Q = - Q и над ней совершается работа dА = - dА. Привести примеры обратимых и необратимых процессов.

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.

В любом из равновесных состояний параметры Р, Т и V термодинамической системы (т.е. газа, жидкости или твердого тела), как показывает опыт, закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение другого. Функциональная связь между давлением, объемом и температурой

f(P,V,N) = 0 (1)

называется уравнением состояния вещества. Если разрешить (1) относительно какого-либо из параметров, например, Р, то уравнение состояния примет вид

Р = Р(V, Т). (2)

Опыт показывает, что для жидкости и твердых тел характер зависимости Р = Р(V, Т) крайне индивидуален. Иначе обстоит дело в случае разреженных газов. Все достаточно разреженные газы подчиняются одному и тому же уравнению состояния – уравнению Клапейрона-Менделеева, которое может быть установлено, как на основе известных опытных газовых законов Бойля-Мариотта (РV = const для данной массы газа), Гей-Люсака [V_t = V₀ (1 + t) для постоянных массы и давлении газа] и Авогадро (при одинаковых Т и Р в равных объемах любого газа содержится одинаковое число молекул), так и на основе молекулярно-кинетической теории строения вещества. Это уравнение имеет вид

PV = MRT/ (3)

или P = MRT/V =  RT/,

где М – масса газа,  - молярная масса, R – газовая постоянная, R=8,31 Дж/мольК,  - плотность газа.

Отношение Z = М/ - число молей газа. Тогда

PV = ZRT (4)

В случае газовой смеси величина Z в уравнении (4) равна полному числу молей всех газов, входящих в смесь

Z = Z₁ + Z₂ +….+ Z_n = М₁/₁ + М₂/₂ + …+ М_n /_n (5)

где М₁, М₂, …,М_n – массы отдельных газов, а ₁ , ₂ , … _n – молярные массы этих газов.

Реальные газы подчиняются уравнению Клапейрона-Менделеева лишь приближенно – при достаточно низких давлениях и высоких температурах. При больших же Р и низких Т у всех газов наблюдаются отклонения от этого уравнения. Газ, который вполне точно подчиняется уравнению Клапейрона-Менделеева, в термодинамике называют идеальным газом. Такого газа в действительности нет, он является некоторой абстракцией, но свойства всех реальных газов приближаются к свойствам идеального газа при малых давлениях. Любой газ в пределе при Р0 неотличим от идеального. Большинство газов уже при атмосферном давлении и комнатной Т близки к идеальному.

Преобразуем (3). Обозначив массу одной молекулы через m, будем иметь М = mN и  = mN_А, где N – общее число молекул газа, а N_А – число Авогадро. Тогда (3) можно записать в виде

PV = NRT/N_A,

но отношение k = R/N_A =1,3810^-23 Дж/К - постоянная Больцмана. Тогда

PV = NkT (6)

В виде (6) уравнение состояния справедливо независимо от того имеем мы дело с химически однородным газом или с произвольной смесью, т.к. оно совершенно не зависит от химической природы газа.

Выражая из (6) Р, получим

Р = NkT/V , но N/V = n – число молекул в единице объема газа, тогда

P = nkT (7)

т.е. давление газа зависит только от его температуры и числа молекул в единице объема газа.
15.БАРОМЕТРИЧЕСКАЯ ФОРМУЛА И РАСПРЕД. БОЛЬЦМАНА.

Если на молекулы газа не действуют никакие внешние силы, то вследствие теплового движения они равномерно распределяются по всему объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число молекул. При одинаковой во всех частях объема температуре в газе устанавливается всюду одинаковое давление Р = nkT = const (в соответствии с законом Паскаля).

Иначе обстоит дело, когда газ находится в некотором силовом поле, в котором на каждую частицу газа действует внешняя сила, толкающая ее в определенном направлении. Под действием такой силы молекулы будут собираться преимущественно в тех областях пространства, куда их заталкивают внешние силы, и там концентрация частиц, а значит, и давление газа будут возрастать. Т.е. действие внешних сил на молекулы газа противоположно тому действию, которое оказывает на них беспорядочное тепловое движение.

В результате одновременного действия внешних сил и теплового движения молекул в газе при заданной температуре устанавливается некоторое неравномерное распределение молекул в пространстве, не изменяемое во времени. Это значит, что при действии внешних сил плотность идеального газа, находящегося в равновесных условиях, будет различной в различных местах пространства, т.е. она будет некоторой функцией координатn= n(X,Y,Z).

Примером внешних сил является поле силы тяжести, а примером газа в таком силовом поле является земная атмосфера. Молекулы газов, составляющие атмосферный воздух, под влиянием теплового движения рассеялись бы в мировом пространстве, если бы отсутствовала сила тяжести. Напротив, если бы отсутствовало тепловое движение молекул, то под действием силы тяжести все молекулы воздуха упали бы на землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли. Таким образом, само существование атмосферы является результатом одновременного действия силы притяжения молекул к Земле и их теплового движения. При этом в атмосфере устанавливается некоторое неравномерное распределение молекул воздуха по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления с высотой.

Если бы земная атмосфера находилась в состоянии теплового равновесия, т.е. температура атмосферы была бы одинаковой на всех высотах, то в ней бы установилось так называемое барометрическое распределение плотности и давления с высотой.

Для определения барометрического закона изменения давления и плотности идеального газа с высотой рассмотрим вертикальный столб газа с площадью поперечного сечения S = 1, находящийся при постоянной температуре, рис.1.

Рис.1.

Обозначим давление газа на некотором нулевом уровне Z = 0 (уровне моря, поверхности земли, дне сосуда и т.д.) через Р₀, а давление на высоте Z над нулувым уровнем через Р. При увеличении высоты на dZ давление газа уменьшится на некоторую величину dР. Это уменьшение давления равно весу столба газа высотой dZ с площадью основания S = 1

dP = - g dZ, (1)

где -  - плотность газа. На основании уравнения состояния идеального газа, его плотность  равна

 = P/RT (2)

Следовательно,

dP = - (P/RT)g dZ,

откуда

dP/P = - (/RT)g dZ.

Интегрируя это выражение, находим

р z

 dP/P = - /R  g dZ/Т

p₀ 0

или z

ln P/P₀ = - /R  g dZ/Т (3)

0

На небольших высотах над поверхностью земли ускорение силы тяжести g можно считать постоянным, не зависящим от высоты Z, и вынести его за знак интеграла . Кроме тего, если газ находится в тепловом равновесии при постоянной, не зависящей от высоты Z температуре Т, то и Т можно вынести за знак интеграла. В этом случае получим

ln P/P₀ = - gZ/RT,

откуда Р/Р₀ = е ^{- gZ/RT}

или Р = Р₀ е ^{- gZ/RT}. (4)

Формула (4) характеризует изменение давления газа с высотой и называется барометрической формулой. Она показывает, что давление газа с высотой убывает по экспоненциальному закону. Характер этого убывания графически можно представить следующим образом, рис.2.


Рис.2.

Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Принцип его действия основан на использовании формулы (4). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

Принимая во внимание, что  = mN_A и R = k N_A , мы можем переписать барометрическую формулу в виде

Р = Р₀ е ^{- mgZ/ kT}.

Так как P = nkT, то эта барометрическая формула выражает также закон убывания плотности газа с высотой

n = n₀е ^{- mgZ/ kT} (5)

где n и n₀ – числа молекул в единице объема газа в точках, разность высот между которыми равна Z. Ввиду чрезвычайно малой массы газовых молекул убывание плотности газа и его давления заметно только при значительных изменениях высоты. В случае небольшого изменения высоты изменение давления и плотности газа оказываются весьма малыми. Поэтому в случае газа, заключенного в сосуд небольшой высоты, действием силы тяжести на молекулы газа можно пренебречь. Поскольку температура атмосферы Земли не постоянна и изменяется с высотой, то для более точного описания изменений ее давления и плотности с высотой в формулы (4) и (5) необходимо вводить соответствующие поправки на изменение температуры.

Поскольку входящая в формулу (5) величина mgZ представляет собой потенциальную энергию молекул в поле тяготения, то эту формулу можно переписать в виде

n = n₀е ^{– U(Z) /kT} (6)

т.е. она выражает закон распределения молекул идеального газа по величине их потенциальной энергии в поле тяготения. Причем величина n₀ имеет смысл числа частиц с потенциальной энергией равной нулю (n = n₀ при U = 0).

В середине 19 века Больцман показал, что для идеального газа, находящегося в любом силовом поле, число частиц, обладающих заданной потенциальной энергией U, определяется формулой, имеющей тот же вид, что и формула (6). Поскольку, в произвольном силовом поле потенциальная энергия частицы может зависеть от всех трех координат, характеризующих ее положение в пространстве, а не только от одной, как это имело место в частном случае поля тяготения, т.е. n = n(X,Y,Z) и соответственно этому U = U(X,Y,Z). Таким образом, в любом силовом поле распределение частиц в пространстве выражается законом

n(X,Y,Z) = n₀е ^{– U(X,Y,Z) / kT} - закон Больцмана (7)

где U(X,Y,Z) – потенциальная энергия частиц во внешнем силовом поле, зависящая от координат той точки, в которой находится частица; n(X,Y,Z) – концентрация частиц в точке с координатами X,Y,Z; n₀ – число частиц в единице объема (концентрация) в том месте пространства, где их потенциальная энергия равна 0.

Больцман показал, что при постоянной Т концентрация частиц убывает с ростом U и возрастает с убыванием U, т.е. частицы концентрируются преимущественно в местах с меньшей потенциальной энергией.

Закон Больцмана (8) является весьма общим законом, применимым не только к идеальному газу, но и ко многим другим системам невзаимодействующих частиц.
16. ДИФФУЗИЯ.

Беспорядочное тепловое движение молекул в газе приводит к тому, что молекулы переносятся с одного места в другое и при столкновении передают друг другу кинетическую энергию и количество движения. Этот перенос молекул и столкновения между ними обуславливают несколько процессов, которые получили название явлений переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся диффузия (обусловлена переносом массы), теплопроводность (обусловлена переносом энергии) и внутреннее трение (обусловлено переносом импульса силы или количества движения).

Если два различных газа привести в соприкосновение друг с другом, то тепловое движение молекул будет перемешивать их до тех пор, пока не образуется однородная смесь молекул, в которой парциальная плотность каждого газа будет одинакова во всем объеме.

Этот процесс постепенного перемешивания 2-х или большего числа газов называется диффузией. Явление диффузии наблюдается также в жидкостях и даже твердых телах. Процесс диффузии заключается в том, что каждая из компонент смеси переходит из тех частей объема, где ее порциальная плотность больше, туда, где она меньше, т.е. в направлении падения парциальной плотности.

Явление диффузии подчиняется закону Фика, который справедлив не только для газов, но и для жидкостей и твердых тел:

J_m = - D d/dx,

где J_m – плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную направлению переноса (оси OX); D – диффузия (коэффициент диффузии); d/dx – градиент плотности (величина векторная), равный скорости изменения плотности на единицу длины Х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки J_m и d/dx противоположны).

Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.

Возникающий при наличии разности концентраций (или парциальных плотностей) диффузионный поток J_m приводит к выравниванию концентраций, т.е. к уменьшению той разности концентраций, которая вызвала этот поток. Такой процесс диффузии, в результате которого происходит выравнивание концентраций компонентов, является нестационарным процессом: при этом как градиент концентрации, так и диффузионный поток изменяются со временем.

Для того, чтобы процесс диффузии был стационарным, необходимо тем или иным путем поддерживать разность концентраций компонент смеси неизменной во времени. Для этого, например, в одной части сосуда необходимо непрерывно добавлять данный компонент, а из другой его части отбирать его в таком же количестве. При стационарной диффузии градиент концентрации остается неизменным во времени. Остается поэтому постоянным и диффузионный поток.

Рассматривая явление диффузии с точки зрения молекулярно-кинетической теории газов, можно получить выражение для коэффициента диффузии

D = V/3,

где V - средняя скорость теплового движения молекул,  - средняя длина свободного пробега молекул газа.

17. ТЕПЛОПРОВОДНОСТЬ.

Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит выравнивание средних кинетических энергий молекул, т.е. иными словами, выравнивание температур.

С макроскопической точки зрения явление теплопроводности заключается в переносе некоторого количества тепла от более нагретой части вещества к более холодной. Существование градиента температуры dT/dX является необходимым условием для возникновения теплопроводности.

Перенос энергии при теплопроводности подчиняется закону Фурье:

J_E = -  dT/dX, (1)

где J_E – плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную направлению переноса (оси ОХ);  - теплопроводность, dT/dX – градиент температуры (величина векторная), равный скорости изменения температуры на единицу длины Х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки J_E и dT/dX противоположны).

Теплопроводность  численно равна плотности теплового потока при градиенте температуры, равном единице.

В стационарных условиях, когда за счет какого-либо внешнего источника энергии градиент температуры dT/dX поддерживается постоянным, тепловой поток также не изменяется со временем. В тех же случаях, когда газ (или другое тело), в котором существует градиент температуры, предоставлен самому себе, т.е. к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Такой процесс будет, конечно, нестационарным.

При рассмотрении явления теплопроводности газов с точки зрения молекулярно-кинетической теории можно показать, что

 = mnVC_V /3 = VC_V /3, (2)

где C_V – удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме),  - плотность газа, V - средняя скорость теплового движения молекул,  - средняя длина свободного пробега молекул газа, m – масса одной молекулы, n – число молекул газа в единице объема.

Формула (2) позволяет выяснить характер зависимости коэффициента теплопроводности газа от его температуры и давления.
18. ВНУТРЕННЕЕ ТРЕНИЕ (ВЯЗКОСТЬ).

Если в газе имеются слои, движущиеся с различными скоростями, то обмен молекулами между этими слоями будет сопровождаться переносом количества движения из одного слоя в другой. Молекулы, переходящие из более быстрого слоя в более медленный, приносят с собой избыток количества движения, который путем столкновений распределяется между молекулами этого слоя, вследствие чего медленно двигавшийся слой ускоряется. Наоборот, молекулы, проникшие в быстрый слой из более медленного, получают от молекул этого слоя некоторое количество движения. Вследствие этого более быстрый слой замедляется. Такой процесс переноса количества движения из одного слоя в другой, приводящий к выравниванию скоростей отдельных слоев, называется внутренним трением или вязкостью газа.

Если разность скоростей движения слоев газа внешними силами поддерживается постояной, то и поток количества движения от слоя к слою будет постоянным (стационарным). С таким случаем мы встречаемся, например, при медленном течении газа по трубе под действием постоянной разности давлений, направленной вдоль движения.

Для жидкостей характерна достаточно плотная упаковка молекул (об этом свидетельствует их малая сжимаемость). Поэтому каждая молекула, постоянно сталкиваясь с соседними молекулами, в течение некоторого времени колеблется около определенного положения равновесия. Время от времени молекула, получив от соседней молекулы достаточную энергию, скачком переходит в новое положение равновесия. Дальность этого скачка  примерно равна размеру молекул (10^-10м). Среднее время , в течение которого молекула колеблется около данного положения равновесия, называется временем оседлой жизни молекулы. Расчеты показывают, что

₀expE/(kT), (1)

где ₀ – средний период колебаний молекулы; E – минимальная энергия, которую нужно сообщить молекуле жидкости, чтобы она могла перейти из одного положения равновесия в другое (Е10^-20 Дж); k – постоянная Больцмана; Т – абсолютная температура жидкости. Для воды при комнатной температуре ₀  10^-13с, а   10^-11с. С повышением температуры подвижность молекул возрастает, время оседлой жизни уменьшается.

При движении жидкости между слоями, перемещающимися с различной скоростью, возникают силы внутреннего трения (вязкости) подобно, как и в газе. Эти силы

направлены так, что ускоряют медленно движущиеся слои или замедляют быстро движущиеся.

Количественно перенос количества движения между слоями, движущимися с различными скоростями, в газах и жидкостях описывается аналогичными уравнениями.

Р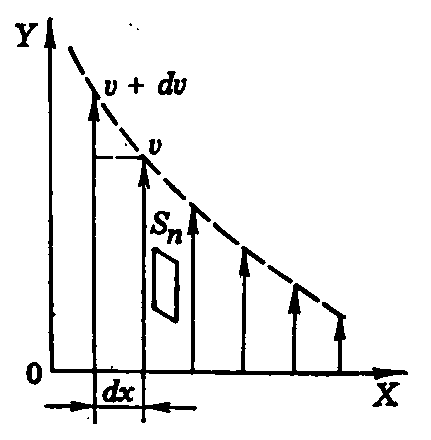
ассмотрим ламинарный поток жидкости или газа в направлении оси Y (рис. 1). Слои движутся с разными скоростями, а скорости двух слоев, отстоящих друг от друга на расстоянии dx, отличаются на dv. Величина – градиент скорости – показывает, как быстро изменяется скорость слоев вдоль оси Х, здесь – единичный вектор в направлении максимального возрастания скорости (в нашем случае в отрицательном направлении оси Х).

Ньютон установил, что модуль силы внутреннего трения между слоями прямо пропорционален площади их соприкосновения и модулю градиента скорости:

(2)

где  – коэффициент пропорциональности, называемый вязкостью (или коэффициентом вязкости) жидкости или газа, соответственно; площадка S_n ориентирована перпендикулярно к градиенту скорости.

Между слоями жидкости (или газа) будет происходить передача импульса. По второму закону Ньютона

, (3)

где dp – величина импульса, переносимого за время dt от слоя к слою через поверхность S_n, перпендикулярную к направлению переноса импульса. Знак минус указывает, что импульс переносится от слоев, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью (в нашем случае вдоль оси Х).

Импульс, переносимый через единичную площадку, расположенную перпендикулярно к переносимому потоку импульса за единицу времени, называется плотностью потока импульса :

. (4)

Соотношения (2)-(4) являются различными формами записи основного закона вязкости - закона Ньютона. Физический смысл вязкости  можно определить из любого соотношения. Например, из (4) следует, что вязкость  определяется плотностью потока импульса при градиенте скорости, равном единице.

Вязкость жидкости зависит от ее химического состава, примесей и температуры. С повышением температуры Т вязкость жидкости уменьшается по закону

=АexpE/(kT). (5)

Здесь коэффициент А для каждой конкретной жидкости можно приблизительно считать постоянным.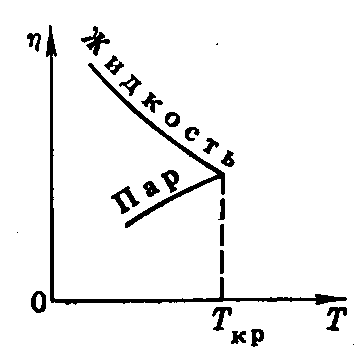



Вязкость газов (паров) в отличие от жидкостей с повышением температуры медленно увеличивается ( ), при критической температуре Т_кр. вязкости жидкости и ее пара сравниваются (рис. 2). Разный характер температурной зависимости вязкости жидкостей и газов указывает на различие механизмов внутреннего трения в них. В газах перенос импульса осуществляется при переходе молекул из слоя в слой благодаря тепловому движению. В жидкостях большую часть времени молекулы колеблются около положения равновесия, скачкообразные переходы редки. Так как молекулы жидкости находятся близко друг к другу, силы молекулярного сцепления между ними значительны. Поэтому одни слои жидкости увлекают (тормозят) соседние слои в основном за счет сил притяжения. Перенос импульса вследствие скачкообразных переходов молекул не играет решающей роли. С повышением температуры расстояния между молекулами увеличиваются, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.

Величина / (6) называется кинематической вязкостью.

Приборы для измерения вязкости называются вискозиметрами. Существует несколько методов определения вязкости: метод Стокса, основанный на измерении скорости падения шарика в исследуемой жидкости; метод Пуазейля, в основе которого лежит измерение объема жидкости (газа), протекающей через капиллярную трубку; метод затухающих колебаний тела, подвешенного на упругой нити в исследуемой среде, и другие.

Молекулярно-кинетическая теория для вязкости газов дает выражение:

 = (1/3)V

где  - средняя длина свободного пробега молекул газа.

20. СТЕПЕНИ СВОБОДЫ МОЛЕКУЛ. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА.

Средняя кинетическая энергия поступательного движения газовых молекул равна

 mV²/2 = 3кТ/2,

где к – постоянная Больцмана, Т – абсолютная температура газа.

Однако, кроме поступательного движения газовых молекул могут совершаться и другие виды движения: вращение и колебание, с которыми тоже связана некоторая энергия. Таким образом, полный запас кинетической энергии молекулы не исчерпывается энергией лишь поступательного движения, она может обладать кинетической энергией вращения и колебания.

Для того чтобы подсчитать среднюю кинетическую энергию молекулы, приходящуюся на все виды ее движения, необходимо ввести понятие о степенях свободы молекулы и выяснить, какая доля общей энергии приходится на одну степень свободы.

Под числом степеней свободы любой механической системы понимают число независимых движений, которые одновременно может совершать эта система; или другими словами, число степеней свободы – это число независимых переменных, определяющих положение системы в пространстве.

Во многих случаях молекулу одноатомного газа можно рассматривать как материальную точку, которой приписывают три степени свободы поступательного движения (вращательными степенями свободы материальная точка обладать не может). Система N материальных точек, могущих двигаться независимо друг от друга, имеет 3N степеней свободы. Если же отдельные точки в системе как-то связаны друг с другом, то число степеней свободы такой системы будет меньше 3N. Например, абсолютно твердое тело, могущее как угодно двигаться в пространстве, обладает 6 степенями свободы, из которых 3 отвечают поступательному движению (три независимо изменяющиеся координаты, определяющие вращение центра тяжести тела) и три – вращательному движению.

Многие газы, например, H₂, O₂, N₂,окись углерода СО и другие состоят из молекул, построенных из двух атомов. В первом приближении двухатомную молекулу можно рассматривать как систему из двух материальных точек, расположенных на некотором расстоянии друг от друга и связанных между собой силами взаимодействия. Можно допустить, что связь между атомами молекул является абсолютно жесткой, т.е. расстояние между атомами не изменяется, тогда такой молекуле следует приписать 5 степеней свободы, а именно: 3 поступательного движения и 2 вращательного движения. Такая молекула кроме трех поступательных движений может совершать еще 2 вращательных движения вокруг 2-х взаимно перпендикулярных осей, составляющих прямой угол с линией, соединяющих атомы. Вращение вокруг самой оси молекул мы не принимаем во внимание, т.к. оно лишено смысла. Таким образом, 2-х атомная молекула обладает пятью степенями свободы (i = 5). Подобно трехатомные и многоатомные линейные молекулы обладают пятью степенями свободы: а именно: 3 поступательного движения и 2 вращательного движения (i = 5). Трехатомные и многоатомные нелинейные молекулы имеют 6 степеней свободы: 3 поступательного и 3 вращательного движения. Естественно, что жесткой связи между атомами не существует. Поэтому для реальных молекул иногда необходимо учитывать также степени свободы колебательного движения. Так 2-х атомная молекула с нежесткой связью между атомами будет обладать, кроме 3 поступательных и 2 вращательных степеней свободы, одной колебательной степенью свободы, соответствующей переменной, определяющей взаимное расстояние между атомами, которое в этом случае будет изменяться. Следовательно, в общем случае 2-х атомные молекулы обладают 6 степенями свободы.

Ни одна из поступательных степеней свободы не имеет преимущества перед другими, все они равноправны, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения средней кинетической энергии поступательного движения молекул газа, а именно

₁₀/3 = (1/2)кТ.

Можно показать, что этот результат относится к вращательному и колебательному движениям молекул, т.е. справедливым является следующее положение: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная кТ/2, а на каждую колебательную степень свободы - в среднем энергия, равная кТ (теорема Больцмана о равномерном распределении энергии по степеням свободы молекул).

Колебательная степень свободы «обладает» вдвое большей энергией, потому что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная энергия, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы

 = (i/2)кТ,

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекул

I = I_пост+ I_вращ + 2i_колеб

В классической теории рассматриваются молекулы с жесткой связью между атомами.

Сумма всех видов энергий движения и взаимодействия частиц тела или системы тел называется внутренней энергией тела или системы. В состав внутренней энергии тела входит энергия всех видов движения, а именно: энергия поступательного и вращательного движения молекул, энергия колебательного движения атомов в молекулах, а также энергия взаимодействия входящих в тело молекул. Внутренняя энергия не включает в себя кинетическую и потенциальную энергию тела, как целого.

Если известен закон взаимодействия между частицами в том или ином теле, то молекулярно-кинетическая теория позволяет рассчитать внутреннюю энергию этого тела. Проще всего определить внутреннюю энергию идеального газа. Так как в идеальном газе взаимодействие между молекулами отсутствует (взаимная потенциальная энергия молекул равна нулю), то его внутренняя энергия складывается только из энергии теплового движения отдельных молекул. Тогда внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий N_А молекул:

U₀ = (i/2)kTN_A = (i/2)RT.

Внутренняя энергия для произвольной массы М газа

U = (M/)i RT/2 = Z i RT/2.

Из полученной формулы видно, что внутренняя энергия данной массы идеального газа зависит только от температуры и совершенно не зависит от объема, занимаемого газом при данной температуре. Для реального газа это не так.

19. РАБОТА И ТЕПЛОТА. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ.

Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате различных процессов, например, совершения над системой работы или сообщения ей теплоты. Для нагревания тела над ним надо совершить работу, а для охлаждения нужно создать такие условия, чтобы оно само могло совершить работу. Известно, что газ, как и всякое другое тело, можно нагреть или охладить (т.е. изменить его внутреннюю энергию) и другим способом, при котором никакая механическая работа не совершается. Для этого тело приводится в контакт с другим телом, имеющим более высокую или более низкую температуру, чем данное тело. При таком контакте происходит обмен энергией между телами, причем одно тело передает внутреннюю энергию другому без совершения работы. Такой процесс изменения внутренней энергии тела без совершения механической работы называется теплопередачей.

Теплопередача осуществляется не только при непосредственном контакте, но и в том случае, когда тела различной температуры разделены какой-либо средой или даже пустотой. В первом случае говорят, что передача осуществляется путем теплопроводности, а в другом – теплоизлучением. Количество энергии, передаваемой одним телом другому при их контакте (непосредственно или через третье тело) или путем излучения называется количеством теплоты. Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Количество теплоты, также как и механическая работа, является мерой изменения энергии тела или системы тел. Энергия механического движения может превращаться в энергию теплового движения, и наоборот.

Работу можно охарактеризовать как макроскопическую форму передачи энергии, связанную с макроскопическим перемещением в системе (например, перемещение поршня в цилиндре с газом), а теплоту – как микроскопическую форму изменения энергии, связанную с микроскопическими процессами, происходящими в системе.

При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.

Если система подвергается одновременно и механическому и тепловому воздействию, то

 Q = dU + A (1)

т.е., бесконечно малое количество тепла, передаваемого системе, идет на бесконечно малое изменение ее внутренней энергии и на элементарную работу, совершаемую системой против внешних сил. Уравнение (1) выражает первое начало термодинамики в дифференциальной форме, т.е. для бесконечно малого изменения состояния системы.

В интегральном виде, т.е для конечного изменения состояния системы первое начало термодинамики имеет вид

Q = U₂ – U₁ + A,

где U₂ – U₁ -изменение внутренней энергии тела или системы при переходе ее из состояния 1 в состояние 2, Q – количество теплоты, полученное при этом системой, и А – полная работа, производимая системой при переходе из 1 состояния во 2-ое.

Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии U = 0. Тогда, согласно первому началу термодинамики,

А = Q,

т.е. вечный двигатель первого рода - периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, - невозможен (одна из формулировок первого начала термодинамики).