1.ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. ЗАКОН КУЛОНА
Из школьного курса физики известны такие электрические явления, как электризация при трении тел, проявление атмосферного электричества - молния. Эти явления обязаны существованию двух видов электрических зарядов, условно названных (+) и (-). Электрический заряд является неотъемлемым свойством так называемых заряженных частиц. Электрический заряд дискретен. Элементарный заряд для различных веществ одинаков по абсолютной величине и обозначается "е". В настоящее время известно десятки элементарных частиц, которые изучаются в курсах ядерной физики. Электрон имеет отрицательный элементарный заряд е-, протон – е+, заряд нейтрона равен нулю. Заряда равного какой-то части «е» не существует, т.е. пока физиками не обнаружен. Кварки.
(me=0,91·10-27г; mp=1,67·10-24г; dp=1,6·10-12м;
Обычно заряды разных знаков присутствуют в веществе в равных количествах и распределяются с одинаковой плотностью. Поскольку заряд тела qобразуется совокупностью элементарных зарядов, то он является целым кратным е±, т.е. q=±Ne.
Электрические заряды могут исчезать и возникать вновь, однако, два элементарных заряда противоположных знаков всегда возникают и исчезают одновременно. Поэтому суммарный заряд электрически изолированной системы не может изменяться, т.е.
-алгебраическая сумма электрических зарядов в замкнутой изолированной системе остается постоянной, Это утверждение носит название закона сохранения электрического заряда (1843 год, М. Фарадей).
Электрический заряд – величина релятивистски инвариантная, т.е. не зависит от системы отсчета, а значит, не зависит от того, движется этот заряд или покоится.
Если электрические заряды могут свободно перемещаться между различными частями тела, то соответствующие тела называются проводниками электричества. Тела, в которых электрические заряды не могут свободно перемещаться между различными частями тела, называются изоляторами или диэлектрикам. Диэлектрики проводят электрический ток хуже проводников в 1015 раз. Существуют вещества с промежуточной между проводниками и диэлектриками проводимостью, которые называются полупроводниками.
Экспериментальное определение величины ,,е" было впервые осуществлено в 1909г. Милликеном.
Опыт показывает, что одноименные электрические заряды отталкиваются друг от друга, разноименные заряды притягиваются друг к другу, а при соединении в равных количествах – нейтрализуются.
Изучение электрических явлений мы начнем с наиболее простого случая, когда электрические заряды статические, а электрические поля не меняются со временем. Взаимные перемещения зарядов нам иногда придется учитывать, но мы будем считать их бесконечно медленными, т.е. настолько медленными, что силы взаимодействия можно предполагать практически не зависящими от скорости движения зарядов.
Закон взаимодействия электрических зарядов был установлен в 1875 Кулоном.
Сила взаимодействия двух точечных зарядов направлена вдоль линии, соединяющей оба заряда, пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между зарядами
 (1)
В векторной форме закон Кулона записывается в следующей форме:
 где 
Эта формула выражает не только величину силы, но и её направление,  -вектор, проведенный из одного заряда в другой, имеет направление к тому из зарядов, к которому приложена сила `F (если заряды одноименны).
 
 (1`)
т.е. взаимодействие электрических зарядов удовлетворяет третьему закону Ньютона.
Коэффициент k зависит от выбора системы единиц. В СИ  ,. где  - электрическая постоянная в вакууме,  -множитель рационализации. = 8,86 ·10-12 Кл2/Н·м2 ); k= 9·109Н·м2/Кл2.
В системе СИ закон Кулона выглядит следующим образом
 (1``)
e -безразмерная величина, характеризующая электрические свойства среды и называющаяся относительной диэлектрической проницаемостью среды,
В системе СИ для измерения электрических величин вводится основная электрическая единица тока - ампер (А). Единицей заряда в СИ является кулон (К) - количество электричества, протекающее за I с через поперечное сечение проводника при токе в цепи, равном I А: 1Кл = 1А·с
Формулы (1) остаются справедливыми и в случае разноименных зарядов. Произведение зарядов в этом случае отрицательно, и обе силы меняют своё направление - отталкивание заменяется притяжением.
Принцип суперпозиции. Если зарядов имеется не два, а больше, то на каждый заряд будут действовать другие заряды с силой типа (1) с результирующей силой  . Опыт показывает, что силы, возникающие в результате электрического взаимодействия, складываются по тем же законам, как и силы в механике, т.е. вектор `F равен геометрической сумме сил `Fi, создаваемых электрическими полями каждого заряда и определяемых по закону Кулона:
`F = S`Fi.
Если заряды взаимодействуют не в вакууме, а в однородной непроводящей среде, то сила взаимодействия между зарядами уменьшается.
 - диэлектрическая проницаемость среды.
Произведение ee0=eа – абсолютная диэлектрическая проницаемость среды.
Пользуясь формулой (1) можно вычислить силу взаимодействия между зарядами, сосредоточенными на телах конечных размеров. Для этого заряженное тело разбивают на бесконечно малые части и, рассматривая их как точечные заряды dq, вычисляют силу взаимодействия создаваемую отдельными зарядами, а затем производят векторное сложение этих сил.
Удаленные друг от друга точечные заряды взаимодействуют по закону Кулона. Возникает вопрос: каким образом осуществляется это взаимодействие, т.е. какой материальный носитель взаимодействия? Этим носителем является связанное с зарядами электрическое поле. Силовые взаимодействия между разобщенными телами могут передаваться только при наличии какой-либо среды, окружающей эти тела, последовательно от одной части этой среды к другой, и с конечной скоростью (теория близкодействия); даже при наличии одного - единственного заряда в окружающем пространстве происходят определённые изменения. Т.о. между зарядами существует электрическое поле, которое и осуществляет их взаимодействие. Если в каком -либо месте появляется электрический заряд, то вокруг этого заряда возникает электрическое поле. Основное свойство электрического поля заключается в том, что на всякий другой заряд (пробный) помещённый в это поле, действует сила.
Для количественной характеристики электрического поля служит специальная физическая величина - напряжённость электрического поля. Согласно закону Кулона, сила, действующая на пробный заряд q', при внесении его в поле других зарядов, пропорциональна величине этого пробного заряда q’. Поэтому силы элeктрического поля будут вполне определены, если определена в каждой точке этого поля сила, действующая на помещенный в ней единичный положительный заряд. Эта сила, действующая на заряд q'=1, называется напряжённостью или силой электрического поля и обозначается `E.
Как следует из закона Кулона, напряжённость поля точечного заряда q на расстоянии r от этого заряда равна:
 ;  ; 
 ;
 - не зависит от величины пробного заряда, единица измерения в СИ - Н/Кл.
Напряжённость поля точечного заряда убывает обратно пропорционально квадрату расстояния от заряда.
Направление вектора `E определяется направлением силы `F, действующей на положительный заряд, помещённый в рассматриваемую точку поля, рис. 1.
РИС.
Из сказанного следует, что если известна напряженность поля в какой-либо точке, то тем самым определена и сила, действующая на электрический заряд, помещённый в эту точку, а именно:
`F=q`E.
Если электрическое поле создается не одним, а несколькими точечными зарядами q1, q2, q3,…qn, то в этом случае результирующая напряженность суммарного силового поля равна
E = `E1+`E2 +`E3 +…+`En = S`Ei.
т. е. вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности( принцип суперпозиции электрических полей). Принцип суперпозиции выполняется лишь тогда, когда электрические поля не меняют свойств среды, т.е. пока внешние поля значительно меньше электрических полей, существующих внутри атомов и молекул.
Возможны случаи, когда электрическое поле создастся не точечным зарядом, а заряженным телом объема V. В этом случае необходимо знать распределение зарядов внутри тела.
Выделим внутри заряженного тела малый объём  и обозначим через  величину электрического заряда, находящегося в этом объёме.
Предел отношения  , когда величина объёма неограниченно уменьшается, называется объёмной плотностью электрических зарядов в данной точке. Обозначим её r.
lim =r
Т.о. объёмная плотность заряда измеряется зарядом единицы объёма тела. В общем случае неравномерно заряженного тела r различно в разных точках. Распределение заряда в объёме известно, если известно r как функция координат.
Очень часто заряды распределяются в телах только внутри тонкого поверхностного слоя. В этом случае удобно пользоваться поверхностной плотностью заряда s, которая определяется аналогично объёмной плотности зарядов
lim =s
Величина заряда, находящегося на элементе поверхности dS, равна sdS. Для задания распределения зарядов на поверхности тела нужно знать s как функцию координат поверхности.
В случае линейного заряженного тела
lim =l- линейная плотность заряда.
Во всех этих трёх случая, если известно распределение зарядов тела, то можно вычислить и электрическое поле, создаваемое этим телом. Для этого заряженное тело разбивают мысленно на бесконечно малые части и, рассматривая их как точечные заряды, вычисляют напряженность поля, создаваемую отдельными частями тела. Полное поле находят затем суммированием (интегрированием) полей, вызываемых отдельными частями тела, например:
2. ЛИНИИ НАПРЯЖЕННОСТИ. ПОТОК ВЕКТОРА НПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Для того, чтобы описать электрическое поле, нужно задать Е в каждой точке поля . Это можно сделать аналитически, выражая зависимость Е(х,у,z) в виде формул. Однако, это можно сделать и графически с помощью так называемых линий напряженности или силовых линий.
Силовой линией, или линией вектора напряженности поля, называют линию, проведенную в электрическом поле, для которой направление касательной в любой точке совпадает с направлением вектора напряженности поля (рис.2)
Рис.2
Т.к. касательная определяет два взаимно противоположных направления, то силовой линии приписывают определенное направление, отмечая его на чертеже стрелкой.
Густота силовых линий на чертеже отражает величину напряженности поля, а именно, число силовых линий, проходящих через единицу поверхности, перпендикулярной к силовым линиям, равно ( или пропорционально) величине напряженности поля в данном месте. Вследствие наглядности графический способ представления полей широко применяют в электротехнике.
Из сказанного следует, что силовую линию можно провести через всякую точку поля. Далее, т.к. в каждой точке поля вектор напряженности имеет вполне определенное (одно!) положение, то силовые линии нигде не пересекаются.
 В качестве примера рассмотрим картину силовых линий точечного заряда. Для точечного заряда `E||`r и линии напряженности направлены по радиусам, проведённым из заряда. Для положительного заряда (q>0) эти линии исходят из заряда и уходят в ¥ (рис.3 а).
Для отрицательного заряда (q<0) `E направлен против радиус-вектора `r, а линии напряженности идут из ¥ и сходятся в точке нахождения заряда (рис.3 б). Как видно из рисунка, густота линий убывает обратно пропорционально квадрату расстояния от заряда, т.е. так же, как и напряженность поля.
Т.е. густота линий равна отношению полного числа линий N к величине поверхности сферы радиуса r, т.е. N/4pr21/r2.
 На рис.4 показано электрическое поле между двумя равными по величине точечными зарядами одинаковых и противоположных (рис.5) знаков, расположенными на расстоянии lдруг от друга (диполь).
Рис.4. Рис.5. (Дипольный момент Р = q l).
Связь между электрическим полем и его источником может быть выражена достаточно просто. Для этого введём понятие потока вектора напряженности, которое используется при формулировке важнейших свойств электрического, магнитного и других векторных полей.
Рассмотрим в пространстве некоторое электрическое поле и замкнутую поверхность произвольной формы.
Разделим всю поверхность на столь малые части, что поверхность каждой части (элемента поверхности) можно считать практически плоской; на такой поверхности вектор напряженности электрического поля не будет заметно меняться. Направление элемента поверхности представим вектором нормали. За положительную нормаль к поверхности примем внешнюю нормаль, т.е. нормаль, направленную наружу. Способ разделения поверхности на элементы не имеет значения, пока элементы достаточно малы. Число силовых линий, равных скалярному произведени
N = (`E×`n)dSi = Фi - называется потоком вектора напряженности через элемент поверхности dSi.
Величина Ф может быть >0 и<0, т.к. нормаль может быть как положительной, так и отрицательной.
Теперь сложим потоки через все элементы поверхности и получим поток через всю поверхность
Ф = ò (`E×`n)dS =ò (En ×dS,
где Еn - проекция `Е на направление нормали к площадке dS, где интеграл берется по поверхности S.
Пусть Вас не пугает сложность вычисления таких интегралов для поверхностей сложной формы. Удивительное свойство, которое мы с вами сейчас рассмотрим, делает такие вычисления ненужными!
Теорема Остроградского-Гаусса.
1). Возьмём наиболее простой случай: предположим, что поле создано изолированным положительным точечным зарядом q и что поверхностью является сфера радиуса r, в центре которой расположен точечный заряд (Риc. 6). Чему равен поток Ф через такую поверхность?
Рис.6.
Ответить на этот вопрос легко, т.к. в каждой точке поверхности
`E = (1/4pe0)(q/r3)`r,
а поверхность сферы S=4pr2, тогда
Ф = E×4pr2= (q/4pe0 r2) 4pr2=q/e0.
Как мы видим из этой формулы, поток не зависит от размеров сферы.
2).Покажем теперь, что поток не зависит и от формы поверхности,окружающей заряд q. Проведем две концентрические сферы разных радиусов. Мы увидим, что число линий напряженности электрического поля, пронизывающих сферы, одинаково. Между этими сферами линии вектора напряженности `Е идут непрерывно, нигде не заканчиваясь и не начинаясь вновь. Поэтому, если мы проведем между этими сферами замкнутую поверхность S1 произвольной формы, тоже охватывающую заряд q, то поток вектора напряженности через эту поверхность также будет равен q/e0.
Напомню, что линии напряженности электрического поля начинаются и заканчиваются только на электрических зарядах. Если замкнутая поверхность не охватывает заряда, то поток вектора электрического поля через эту поверхность равен нулю, т.к. число силовых линий, входящих в поверхность, равно числу выходящих из неё.
3). Пусть поле создается не одним точечным зарядом, а произвольной системой точечных зарядов q1, q2, q3…qn. По принципу суперпозиции напряжённость результирующего электростатического поля равна векторной сумме напряжённостей электростатических полей, создаваемых каждым из зарядов в отдельности :
`E = `E1+`E2 +`E3 +…+`En = S`Ei.
поэтому проекция вектора `Е на направление нормали к площади dS равна алгебраической сумме проекций всех векторов `Еi на это направление
Поток напряженности результирующего поля сквозь произвольную замкнутую поверхность S, охватывающую заряды q1, q2, …qk , и не охватывающую заряды qk+1…qm, равен  , но Фi=0, если i>k
поэтому
 ,т.е.
поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов, охватываемых этой поверхностью, к электрической постоянной. Это и есть теорема Оетроградского -Гаусса применительно к электростатическому полю в вакууме.
Теорема Остроградского-Гаусса выведена нами как прямое следствие из закона Кулона. Она позволяет сравнительно просто рассчитывать электрические поля при симметричных распределениях зарядов и окружающих их диэлектриков.
Для характеристики электрического поля наряду с `Е удобно ввести ещё одну векторную величину `D , называемую электрическим смещением или электрической индукцией. Для поля в электрически изотропной среде связь `D и `E в СИ имеет вид
D = ee0 `E
Тогда к
 -теорема Остроградского-Гаусса.
Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью.
Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Остроградского-Гаусса.
Пример 1. Равномерно-заряженная плоскость.
Имеется безграничная плоскость, заряженная равномерно с поверхностной плотностью заряда s. Найти напряженность Е(х), где х - расстояние до плоскости.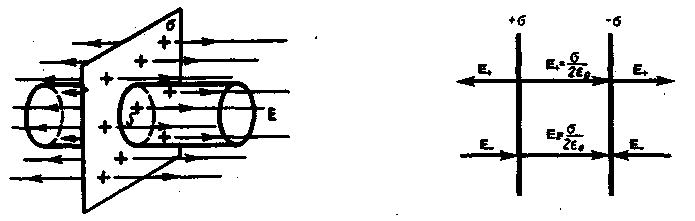
 Из симметрии задачи очевидно, что линии напряженности должны быть направлены симметрично в обе стороны от плоскости ^ ей. В этом случае в качестве замкнутой поверхности в теореме Остроградского-Гаусса удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограниченный двумя плоскими основаниями, перпендикулярными к силовым линиям и расположенными по обе стороны заряженной плоскости (рис.7).
Рис. 8.
Т.к. образующие цилиндра параллельны вектору напряженности электрического поля `Е, то поток через боковую поверхность цилиндра равен нулю и поэтому полный поток сквозь цилиндр равен сумме потоков через его основания
Ф =:2ЕS.
Полный заряд, заключенный внутри цилиндра равен Ss. Поэтому применяя теорему О-Г, имеем:
2ЕS =sS/e0, откуда
Е = s/2e0,
т.е. `Е не есть функция расстояния. Следовательно `Е = соnst по величине и по направлению.
Если плотность заряда отрицательная, т.е. (-s), то линии напряжённости имеют противоположное направление.
Пример2. Определим поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноимёнными зарядами (плоский конденсатор, рис.8). Считаем плоскости бесконечными.
Заряженная плоскость каждой пластины создаст по обе стороны от себя напряженность поля, выражаемую формулой ±s/2e0. Внутри металлических пластин и вне конденсатора эти поля направлены противоположно и поэтому в сумме дают нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и, складываясь, дают у поверхности пластин напряженность Е = s/e0. В данном частном случае электрическое поле однородно и поэтому его напряженность у поверхности пластин такая же, как и в других точках поля.
Пример 3. Равномерно заряженный шар.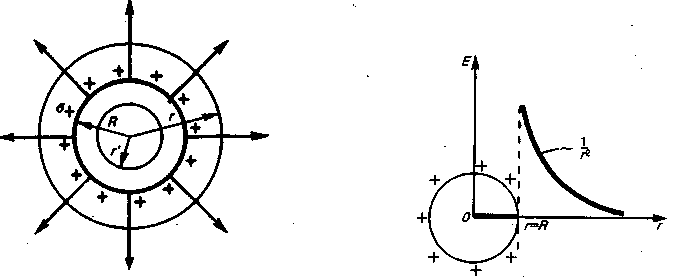
 Рассмотрим электрическое поле между двумя шаровыми концентрическими электродами (рис.9) - шаровой конденсатор. Под действием взаимного притяжения (-) и (+ ) заряды расположатся только на Рис.9. Рис10
поверхности внутреннего шара и на внутренней поверхности внешнего электрода. Из условий симметрии очевидно, что заряды на обоих шаровых электродах будут распределены равномерно, и что линии напряженности электрического поля могут быть только радиальными прямыми. Выберем в качестве замкнутой поверхности сферу с радиусом r, расположенную между электродами и имеющую общий центр с обоими электродами.
По теореме Остроградского-Гаусса
Ф = Е(r)4pr2 = q/e0,
откуда
Е(r)=q/4pe0r2. (*)
Эта формула показывает, что напряжённость поля между электродами зависит от расстояния r рассматриваемой точки поля от центра внутреннего шара, но не зависит вовсе от размеров внешнего электрода. Ту же напряженность поля получим, если радиус внешнего электрода будет как угодно велик. Роль внешнего электрода могут играть различные удалённые заземлённые предметы, например стены, пол и потолок комнаты. Поэтому часто говорят просто о поле заряженного шара (рис.10), не указывая, что именно является вторым электродом. Из формулы (*) следует, что электрическое поле шара, равномерно заряженного по поверхности, во внешнем пространстве совпадает с полем точечного заряда, равного полному заряду шара и помещённого в центре шара. Если бы мы рассмотрели шар, заряженный равномерно по объёму, то напряженность поля тоже выражалась бы формулой (*). Напряженность же поля внутри шара в обоих случаях различна. В случае шара, равномерно заряженного по поверхности Е = О в любой внутренней точке. Если же шар заряжен равномерно по объёму, то Е= 0 только в центре шара и с увеличением расстояния r от центра возрастает пропорционально r. В справедливости этого можно убедиться также при помощи теоремы Остроградского-Гаусса.
Пример: «клетка Фарадея».
РИС.
|
Скачать 2.4 Mb.