КУРСОВАЯ. 1 Основные определения и типы электрических переходов
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
   СОДЕРЖАНИЕ ВВЕДЕНИЕ…………………………………………………………………………..3 1 Основные определения и типы электрических переходов……………………...4 2 Расчет характеристик резкого p-n перехода…………………………………......12 2.1 Контактная разность потенциалов……………………………………………...14 2.2 Ширина запирающего слоя и его частей…………………………………….…14 2.3 Распределение напряжённости электрического поля………………………....15 2.4 Распределение потенциала электрического поля……………………………...16 2.5 Вольт-амперная характеристика идеального p-n перехода…………………...17 2.6 Барьерная и диффузионная ёмкости……………………………………………18 2.7 Дифференциальное и статическое сопротивление…………………………….21 ЗАКЛЮЧЕНИЕ………………………………………………………………………21 ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННЫХ ИНФОРМАЦИОННЫХ РЕСУРСОВ.....…..22 ВВЕДЕНИЕ На основе электрических переходов было создано огромное количество электроприборов, таких как различные типы диодов, биполярные и полевые транзисторы, симисторы, динисторы, тиристоры и др. Для более эффективного использования этих устройств, необходимо знать свойства электрического перехода и уметь рассчитывать его параметры. Цель работы: более глубоко познакомиться с различными типами электрических переходов, технологиями получение P-n переходов, физическими основами процессов, протекающих в p-n переходе, освоить методику расчёта важнейших параметров и характеристик резкого (идеального) p-n перехода и усвоить их взаимосвязь. Задания курсовой работы: - Рассчитать контактную разность потенциалов на p-nпереходе; - Рассчитать полную ширину запирающего (обеднённого зарядами) слоя p-n перехода, а также ширину частей этого слоя в p- и n- областях перехода; - Рассчитать и построить распределение напряжённости электрического поля в запирающем слое p-n перехода вдоль оси X, направленной слева на право от области p к области n перехода. Определить максимальное по модулю значение напряжённости электрического поля в переходе; - Рассчитать и построить распределение потенциала электрического поля в запирающем слое p-n перехода вдоль оси X, направленной слева на право от области p к области n перехода; - Рассчитать обратный ток насыщения через p-n переход. На основании полученного значения рассчитать и построить вольт-амперную характеристику идеального p-n перехода; - Рассчитать и построить зависимости барьерной и диффузионной ёмкостей от значения приложенного к переходу напряжения; - Рассчитать дифференциальное и статическое сопротивление p-n перехода для значения прямого внешнего напряжения на переходе. Основные определения и типы электрических переходов Электрическим переходом в полупроводнике называется граничный слой между двумя областями, физические характеристики которых имеют существенные физические различия. Типы электрических переходов. Электронно-дырочным или p-n-переходом называют переходный слой, возникающий при контакте двух полупроводников с различным типом электропроводности. Получить p-n-переход непосредственным соприкосновением двух полупроводников практически невозможно, так как на их поверхности содержится огромное количество примесей, загрязнений и всевозможных дефектов, резко меняющих свойства полупроводников. Для создания p-n-переходов используют различные технологические приемы, изменяющий тип электропроводности той или иной области монокристалла. Например, путем диффузии в монокристалл p-типа донорских примесей можно получить в нем область n-типа. Р-n-переход, у которого концентрации дырок и электронов практически равны Np Nn , называют симметричным. Если концентрации основных носителей заряда различны Nn Nр или Np Nn) и отличаются в 100…1000 раз, то такие переходы называют несимметричными. Рассмотрим монокристалл полупроводника, в котором, с одной стороны, введена акцепторная примесь, обусловившая возникновение здесь электропроводности типа p, а с другой стороны, введена донорная примесь, благодаря которой там возникла электропроводность типа n. Каждому подвижному положительному носителю заряда в области p (дырке) соответствует отрицательно заряженный ион акцепторной примеси, но неподвижный, находящийся в узле кристаллической решетки, а в области n каждому свободному электрону соответствует положительно заряженный ион донорной примеси, в результате чего весь монокристалл остается электрически нейтральным. Свободные носители электрических зарядов под действием градиента концентрации начинают перемещаться из мест с большой концентрацией в места с меньшей концентрацией. Так, дырки будут диффундировать из области p в область n, а электроны, наоборот, из области n в область p. Это направленное навстречу друг другу перемещение электрических зарядов образует диффузионный ток p-n-перехода. Но как только дырка из области p перейдет в область n, она оказывается в окружении электронов, являющихся основными носителями электрических зарядов в области n. Поэтому велика вероятность того, что какой-либо электрон заполнит свободный уровень и произойдет явление рекомбинации, в результате которой не будет ни дырки, ни электрона, а останется электрически нейтральный атом полупроводника [1]. В современных полупроводниковых приборах помимо контактов с p-n-переходом применяются контакты «металл – полупроводник». Контакт «металл – полупроводник» возникает в месте соприкосновения полупроводникового кристалла n- или р-типа проводимости с металлами. Происходящие при этом процессы определяются соотношением работ выхода электрона из металла AM и из полупроводника An. Под работой выхода электрона понимают энергию, необходимую для переноса электрона с уровня Ферми на энергетический уровень свободного электрона. Чем меньше работа выхода, тем больше электронов может выйти из данного тела. В результате диффузии электронов и перераспределения зарядов нарушается электрическая нейтральность прилегающих к границе раздела областей, возникает контактное электрическое поле и контактная разность потенциалов: 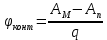 (1.1) (1.1)Переходный слой, в котором существует контактное электрическое поле при контакте «металл-полупроводник», называется переходом Шоттки, по имени немецкого ученого В. Шоттки, который первый получил основные математические соотношения для электрических характеристик таких переходов. Контактное электрическое поле на переходе Шоттки сосредоточено практически в полупроводнике, так как концентрация носителей заряда в металле значительно больше концентрации носителей заряда в полупроводнике. Перераспределение электронов в металле происходит в очень тонком слое, сравнимом с межатомным расстоянием. В зависимости от типа электропроводности полупроводника и соотношения работ выхода в кристалле может возникать обедненный, инверсный или обогащенный слой носителями электрических зарядов [2]. Гетеропереходом называют переходный слой с существующим там диффузионным электрическим полем между двумя различными по химическому составу полупроводниками, обладающие различной шириной запрещенной зоны. Для получения гетеропереходов хорошего качества необходимо, чтобы у материалов, образующих переход с высокой точностью, совпадали два параметра: температурный коэффициент расширения и постоянная кристаллической решетки, что ограничивает выбор материалов для гетеропереходов. В настоящее время наиболее исследованными являются пары: германий – арсенид галлия (Ge-GaAs), арсенид галлия – фосфид индия (GaAs-InP), арсенид галлия – арсенид индия (GaAs-InAs), германий – кремний (Ge-Si). Каждый из полупроводников, образующих гетеропереход, может иметь различный тип электропроводности. Поэтому для каждой пары полупроводников, в принципе, возможно осуществить четыре типа гетероструктур: p1 – n2 ; n1 – n2 ; n1 – p2 и p1 – p2 . При образовании гетероперехода из-за разных работ выхода электронов из разных полупроводников происходит перераспределение носителей заряда в приконтактной области и выравнивание уровней Ферми в результате установления термодинамического равновесия. Остальные энергетические уровни и зоны должны соответственно изогнуться, т. е. в гетеропереходе возникают диффузионное поле и контактная разность потенциалов. При этом энергетический потолок верхней свободной зоны должен быть непрерывным. Энергетический уровень потолка верхней свободной зоны является энергетическим уровнем потолка зоны проводимости, т. к. свободные энергетические зоны перекрывают друг друга [3]. Контактная разность потенциалов рассчитывается по формуле где: - q- заряд электрона , k - постоянная Больцмана, T - абсолютная температура, - Nd - Концентрация доноров, Na - Концентрация акцепторов, ni - cобственная концентрация носителей заряда. Зная, что 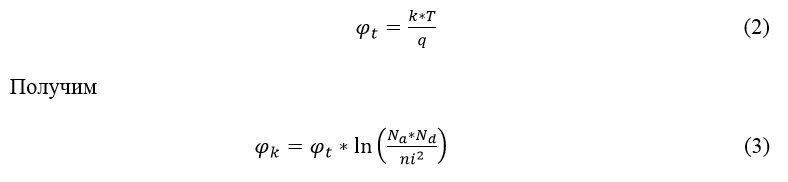 Полная ширина d запирающего слоя: 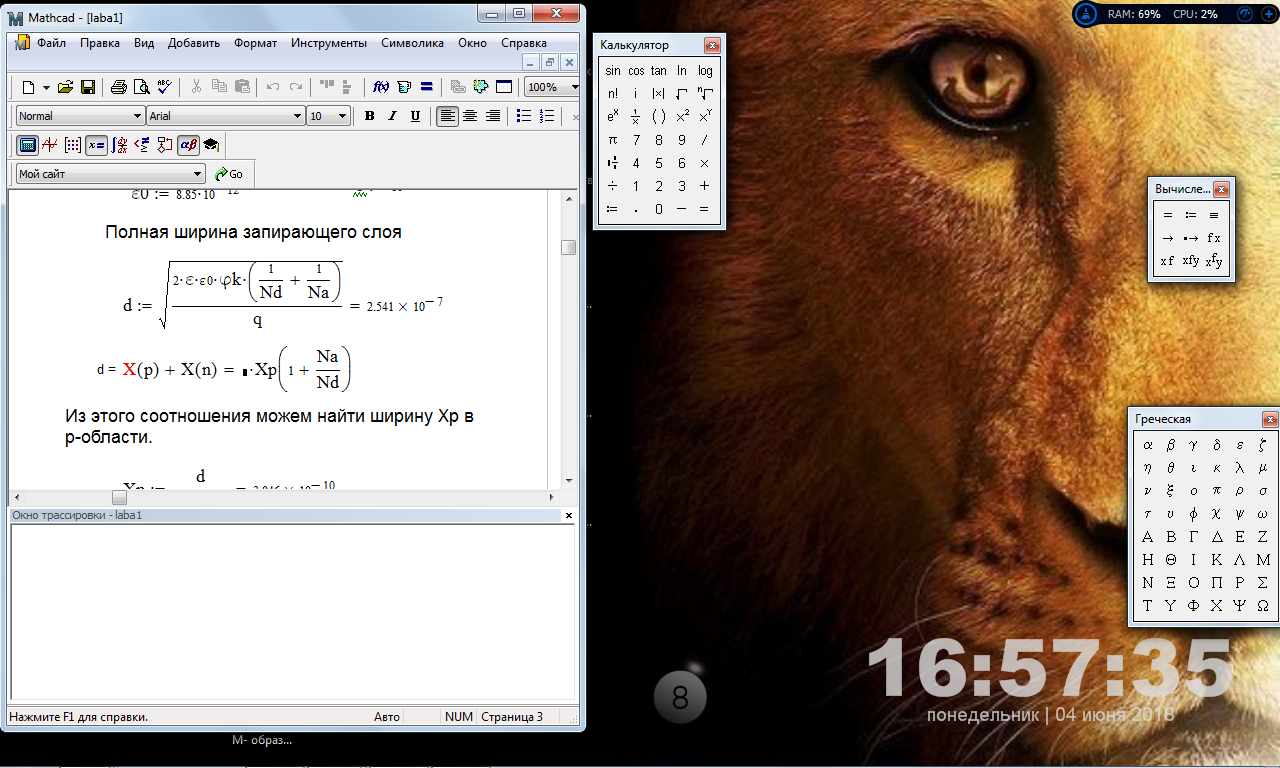 где: - ε - относительная диэлектрическая проницаемость, ε0 - диэлектрическая постоянная, - 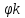 - контактная разность потенциалов, q – заряд электрона, Nd - концентрация доноров, Na - концентрация акцепторов. - контактная разность потенциалов, q – заряд электрона, Nd - концентрация доноров, Na - концентрация акцепторов.Ширина частей в –p и –n областях: 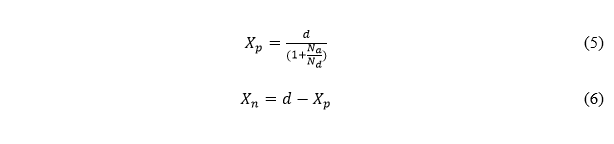 Распределение напряженности электрического поля: 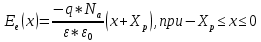 (7) (7)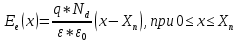 (8) (8)Распределение потенциала электрического поля в резком p-n-переходе: 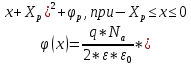 (9) (9)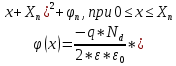 (10) (10)Обратный ток насыщения рассчитывается по формуле: где S– площадь перехода,Dpи Dn– коэффициенты диффузии, LpиLn–диффузионные длины. 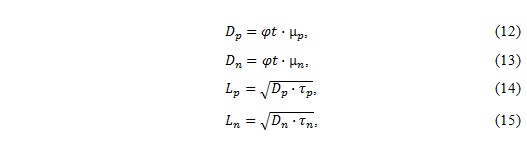 где: - 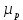 – подвижность дырок, – подвижность дырок, 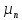 – подвижность электронов, – подвижность электронов, - 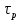 и и 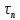 – время жизни неравновесных носителей – электронов и дырок. – время жизни неравновесных носителей – электронов и дырок.Для построения вольт-амперной характеристики нам потребуется формула для нахождения тока: 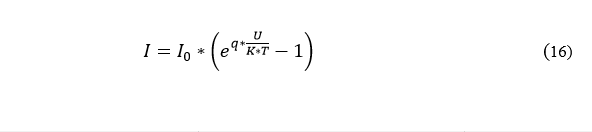 где е – основание натурального логарифма. Формула для нахождения барьерной ёмкости: 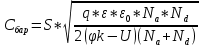 (17) (17)где U- приложенное к переходу напряжение. Формула для расчета диффузионной ёмкости: Формула для расчета диффузионной емкости (полная): 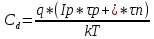 (18) (18)где 𝐼𝑝 – ток инжекции дырок, 𝐼𝑛 – полный ток инжекции (диффузии) электронов 𝜏𝑝 - время жизни дырок, 𝜏𝑛 - время жизни электронов. Формула для расчета полного тока инжекции электронов: 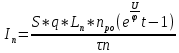 (19) (19)где 𝑛𝑝0 – равновесная концентрация электронов в p-области, 𝐿𝑛 - диффузионная длина электронов, определяемая как 𝐿𝑛=√𝐷𝑛𝜏, где 𝐷𝑛 - коэффициент диффузии электронов. Формула для расчета тока инжекции дырок: 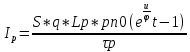 (20) (20)где 𝐿𝑝 – диффузионная длина дырок, 𝑝𝑛0 – равновесная концентрация дырок в n-области. Формула для расчета диффузионной емкости (упрощенная): При wn>Lp функция sch(wn/Lp)≈0 соотношение (18) принимает вид: Если wn  (22) (22)Статическое сопротивление рассчитывается по формуле: 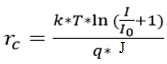 (23) (23)где U - прямое внешнее напряжение на переходе Дифференциальное сопротивление найдем из : 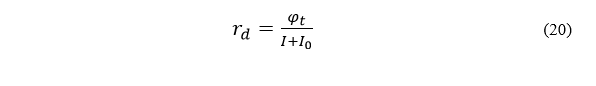 (24) (24)Расчёт характеристик резкого p-n перехода Задания на выполнение курсовой работы: Рассчитать контактную разность потенциалов на p-n-переходе. Рассчитать полную ширину d запирающего (обеднённого зарядами) слоя p-n-перехода, а также ширину частей этого слоя в р- и n-областях перехода. Рассчитать и построить распределение напряжённости электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Определить максимальное по модулю значение напряжённости электрического поля в переходе. Рассчитать и построить распределение потенциала электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Принять значение потенциала в р-области вдали от перехода равным φр = 0. Рассчитать обратный ток насыщения I0 через p-n-переход. На основании полученного значения I0 рассчитать и построить вольт-амперную характеристику идеального p-n-перехода для значений напряжения на переходе, лежащих в диапазоне: -5 В ≤ U ≤ 0,8 В. Рассчитать и построить зависимости барьерной и диффузионной ёмкостей p-n-перехода от значения приложенного к переходу напряжения. Для барьерной ёмкости следует использовать напряжения из диапазона: -10 В ≤ U ≤ (φк – 0,1) В. Для диффузионной ёмкости следует использовать напряжения из диапазона: 0 B ≤ U ≤ U*, где U* - прямое напряжение на p-n-переходе, соответствующее току через переход I = 1 А. При расчёте диффузионной ёмкости учесть, что диффузионная длина дырок в базе (n-области перехода) существенно меньше длины базы. 7 Рассчитать дифференциальное и статическое сопротивление p-n-перехода для значения прямого внешнего напряжения на переходе UВ (задаётся по вариантам)
Значения констант и постоянных параметров для всех вариантов заданий: постоянная Больцмана k = 1,38·10-23 Дж/K; заряд электрона q = 1,6·10-19 К; диэлектрическая постоянная ε0 = 8,85·10-12 Ф/м; абсолютная температура Т = 300 К; 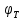 – тепловой потенциал (при комнатной температуре 20 – тепловой потенциал (при комнатной температуре 20 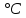 ), ), 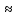 0,025эВ. 0,025эВ.Вариант №3 2.1 Контактная разность потенциалов Рассчитать контактную разность потенциалов на p-n-переходе. Чтобы найти контактную разность потенциалов, воспользуемся формулой (3): 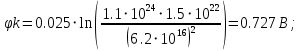 Ответ: 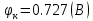 2.2 Ширина запирающего слоя и его частей Рассчитать полную ширину запирающего (обеднённого зарядами) слоя p-n-перехода, а также ширину частей этого слоя в р- и n-областях перехода. Для решения воспользуемся формулами (4), (5), и (6).  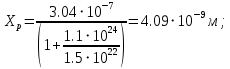 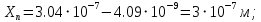 Ответ: 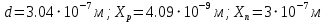 2.3 Распределение напряжённости электрического поля Рассчитать и построить распределение напряжённости электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Определить максимальное по модулю значение напряжённости электрического поля в переходе. Для расчета и построения воспользуемся формулами (7) и (8). Максимальное по модулю значение достигается при x = 0. Найдем его. 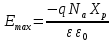 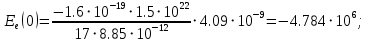 Данный график можно построить, зная 3 точки: 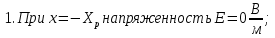 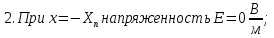   Рисунок 1 – График распределения напряжённости электрического поля в запирающем слое p-n-перехода Ответ: 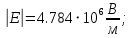 2.4 Распределение потенциала электрического поля Рассчитать и построить распределение потенциала электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Принять значение потенциала в р-области вдали от перехода равным φр = 0. 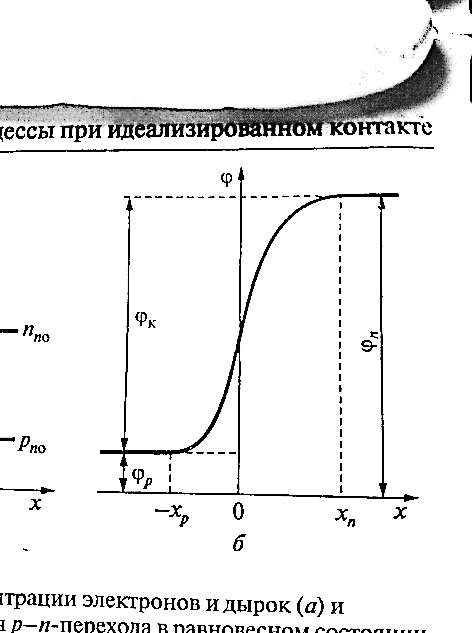 Рисунок 1.1 Распределение потенциала электрического поля для p-n-перехода Из условия дано φр = 0, следовательно, φk= φn. Зная φn выражения принимают следующий вид: 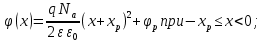 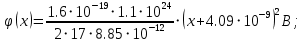 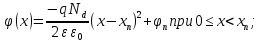 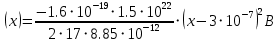 . .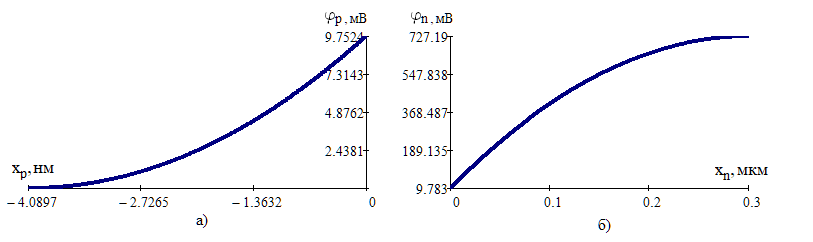 Рисунок 2 –Распределение потенциала электрического поля в запирающем слое р-n-перехода вдоль оси Х, направленной слева на право от области р (а) к области n (б) перехода 2.5 Вольт-амперная характеристика идеального p-n перехода Рассчитать обратный ток насыщения I0 через p-n-переход. На основании полученного значения I0 рассчитать и построить вольт-амперную характеристику идеального p-n-перехода для значений напряжения на переходе, лежащих в диапазоне: -5 В ≤ U ≤ 0,8 В. Для расчета обратного тока насыщения сначала необходимо посчитать диффузионную длину и коэффициенты диффузии (формулы 12,13,14,15): 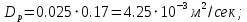 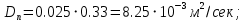 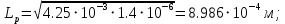 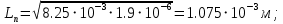 Теперь, рассчитаем обратный ток по формуле (11): 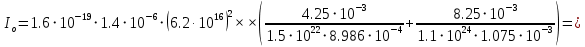 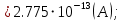 Для построения вольт-амперной характеристики воспользуемся формулой (11): 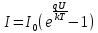 В ходе решения были получены точки, по которым и был построен график ниже. 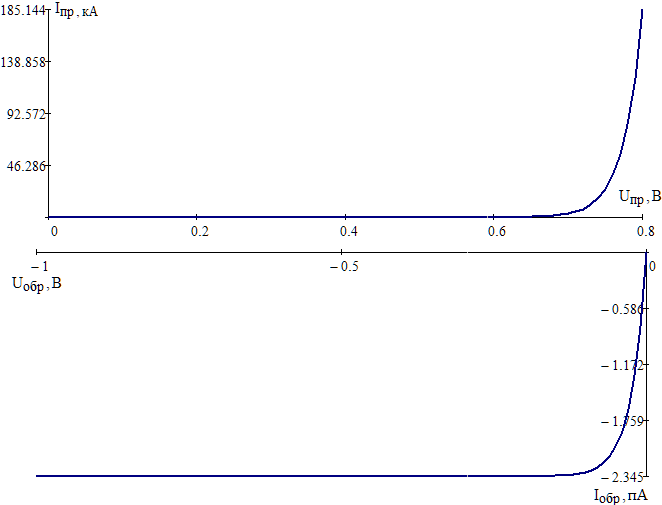 Рисунок 3 – ВАХ идеального p-n-перехода для значений напряжения на переходе, лежащих в диапазоне: -0.6 В ≤ U ≤ 0.8 В На данном рисунке степень величин, отложенных по оси ординат, отрицательная. Ответ: 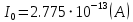 2.6 Барьерная и диффузионная ёмкости Рассчитать и построить зависимости барьерной и диффузионной ёмкостей p-n-перехода от значения приложенного к переходу напряжения. Для барьерной ёмкости следует использовать напряжения из диапазона: -10 В ≤ U ≤ (φк – 0,1) В. Для диффузионной ёмкости следует использовать напряжения из диапазона: 0 B ≤ U ≤ U*, где U* - прямое напряжение на p-n-переходе, соответствующее току через переход I = 1 А. Для решения данного задания воспользуемся формулами (17) и (18). Построим зависимость барьерной ёмкости от напряжения. Воспользовавшись формулой (17), нашел данные точки, по которым и буду строить график. 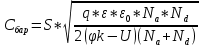 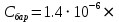 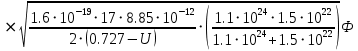 где U- приложенное к переходу напряжение. Формула для расчета диффузионной емкости (полная): 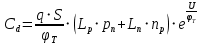 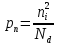 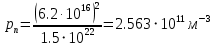 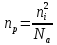 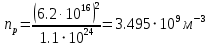 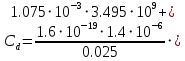 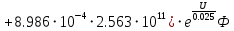 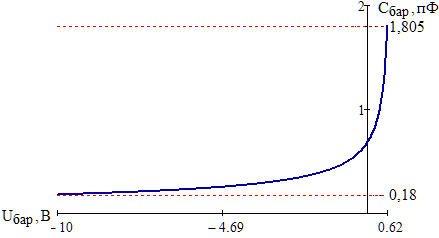 Рисунок 4 – Зависимость барьерной ёмкости от напряжения Далее, с помощью формулы (18) рассчитаем точки и по ним построим график зависимости диффузионной ёмкости от напряжения. 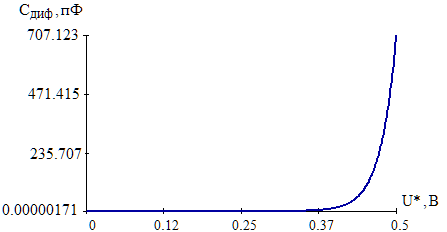 Рисунок 5 – Зависимость диффузной ёмкости от напряжения 2.7 Дифференциальное и статическое сопротивление Рассчитать дифференциальное и статическое сопротивление p-n-перехода для значения прямого внешнего напряжения на переходе UВ (задаётся по вариантам). 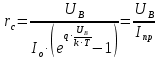 При U=0,9 рассчитаем ток по формуле (16). Он равен: 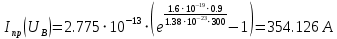 . .Статическое сопротивление равно: 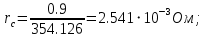 Рассчитаем дифференциальное сопротивление: 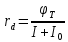 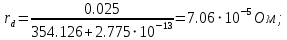 Ответ: 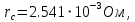 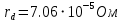 ЗАКЛЮЧЕНИЕ В данной курсовой работе были проведены расчёты и построены зависимости таких параметров резкого p-n перехода как: Контактная разность потенциалов; Ширина запрещающего слоя и его частей; Распределение напряжённости электрического поля; Распределение потенциала электрического поля; Обратный ток насыщения и вольт-амперная характеристика; Барьерная и диффузионная ёмкости; Дифференциальное и статическое сопротивления. ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННЫХ ИНФОРМАЦИОННЫХ РЕСУРСОВ 1 Петров, К.С. Радиоматериалы, радиокомпоненты и электроника: учеб. пос. для студентов вузов - С.Пб.: ПИТЕР, 2003. 103 с. 2 Гусев, В.Г. Электроника и микропроцессорная техника: Учеб. для вузов / В.Г. Гусев, Ю.М. Гусев. – 4-е изд., доп. – М.: Высш. шк., 2006. 530 с. 3 Шишкин, Г. Г. Электроника: учеб. для вузов/ Г. Г. Шишкин, А. Г. Шишкин. - М.: Дрофа, 2009. 610 с.                                           ИСОиП (филиал) ДГТУ г.Шахты Кафедра РЭСиК Курсовая работа «Расчёт параметров и характеристик резкого p-n-перехода» Окорочков А.И. Коликов К.А Окорочков А.И Разраб. Провер. 3.3 Реализация задачи Н.контр. Утв. Лит Лист Изм Подпись Дата Лист Листов 2 Э.170000.000 ПЗ № докум. |
