Методы оптимизации. Конспекты по методам оптимизации. 1. основные положения оптимизации

• Название: 1. основные положения оптимизации
• Анкор: Методы оптимизации
• Дата: 19.04.2023
• Размер: 318.5 Kb.
• Имя файла: Конспекты по методам оптимизации.doc
• Тип: Задача; #1073516
• страница: 4 из 4

1.4. Классификация методов оптимизации

Классификация методов оптимизации представляет собой достаточно сложную задачу, так как в основном они исторически развивались независимо один от другого с использованием различных концепций, математических аппаратов и т.д. Однако специалисту по информатике и вычислительной технике необходимо ознакомиться с ними.

Разумеется, что приводимая классификация (как и любая классификация) носит условный характер, но в целом она позволяет сразу охватить все особенности методов.

Возможно несколько подходов к классификации. Следует различать методы определения экстремума функции и функционала (рис. 7). Поскольку функция является частным случаем функционала, методы отыскания экстремума функции проще. Методы динамического программирования и принципа максимума применяются для отыскания экстремума функционала и функции. Прямые методы вариационного исчисления (методы Ритца, Эйлера и др.), как и дискретный вариант уравнения Эйлера, сводят задачу отыскания экстремума функционала к экстремуму функции.

Методы отыскания экстремума функции получили большое развитие в связи с вычислительными трудностями решения системы алгебраических уравнений вида

dF (x₁, x₂, ..., x_n)/dx_j = 0, j = 1, 2, ..., n,

особенно при наличии ограничений на координаты x_j.

Классическая математика ограничивалась разработкой методов решения и доказательствами принципиальной разрешимости таких систем уравнений, что привело к созданию аналитических методов оптимизации (методы принципиальной разрешимости уравнений оптимизации). При решении конкретных задач важно владеть процедурами, позволяющими доводить решение до числовых данных. Это заставило искать и разрабатывать численные методы оптимизации (методы решения конкретных инженерных задач с доведением решения до числовых данных). Практика проектирования конкретных систем управления требует применения обоих методов.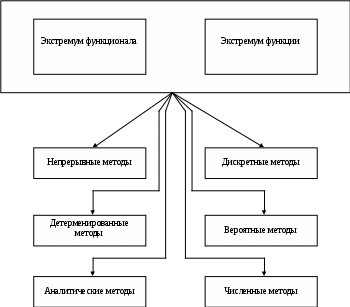




Рис. 7. Схема методов оптимизации

За аналитическими методами остается преимущество, заключающееся в возможности определения качественной картины поведения оптимальной системы при изменении ее параметров и структуры. Численные же методы обеспечивают получение конкретных числовых значений параметров. Рациональное объединение этих методов производится при разработке человеко-машинных методов оптимизации, использующих диалог человека и ЭВМ, базы данных и возможности современных телекоммуникационных систем. При этом обычно повторяют вычисления, изменяя условия, используя, где необходимо, аналитические методы, представленные в виде стандартных библиотечных программ, и, самое главное, оперативно включая в процедуру отыскания оптимального управления интеллектуальные способности человека.

При таком способе оптимизации исходный критерий оптимальности может быть математически нестрого формализован в виде функции или функционала. Так, он может состоять из нескольких положений, сформулированных достаточно четко на словесном, содержательном уровне, что при наличии диалога человек-машина вполне допустимо.

В задачах с ограничениями большое развитие получили методы линейного и нелинейного программирования, прямые методы отыскания экстремума функции, а также дискретные принципы максимума и динамическое программирование (рис. 8).



Рис. 8. Методы отыскания экстремумов функций
Методы отыскания экстремума функционала ведут свое начало от классических методов Эйлера-Лагранжа-Гамильтона и заканчиваются динамическим программированием и принципом максимума (рис. 9). В них также содержатся прямые методы отыскания экстремума функционала и различные частные методы.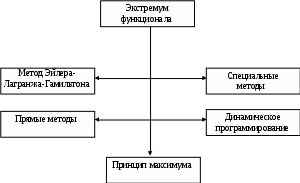


Рис. 9. Методы отыскания экстремумов функционалов
Почти во всех методах:

– Эйлера — Лагранжа — Гамильтона;

– принципе максимума;

– динамическом программировании;

– прямых методах отыскания экстремума функции

можно выделить дискретные и непрерывные модификации, детерминированные и случайные варианты.

Дискретная задача оптимизации возникает всякий раз, когда требуется найти оптимальное значение переменных, которые заданы, так же как и функция от них, в виде набора дискретных значений.

В связи с разработкой автоматизированных информационных систем управления (АИСУ) большое значение приобрели методы целочисленного программирования. Одна из основных задач АИСУ – оперативно-календарное планирование, относится к задачам целочисленного программирования. Единого общего метода решения задач целочисленного программирования нет. Разработано много способов решения пригодных для частного класса задач, среди которых большое место занимают нестрогие эвристические методы. Особого внимания среди них заслуживают лингвистические методы оптимизации (методы, имитирующие применяемые человеком методы оптимизации и планирования с добавлением эффективных аналитических и числовых процедур). Они ближе всего подходят к человеческому способу мышления и удобны для реализации на ЭВМ с помощью проблемно-ориентированных языков. Человеко-машинные методы решения целочисленных задач оптимизации являются по существу своему лингвистическими в широком смысле.

В заключение надо отметить, что одни и те же методы, рассматриваемые с разных точек зрения, могут использоваться как аналитические и как численные. Так, градиентный метод используется в прямых методах отыскания экстремума функции и методах нелинейного (квадратичного и выпуклого) программирования. Во втором случае он используется как аналитический, в первом – как численный метод.

1.5. Системный анализ и оптимизация

Системный анализ - это синтез идей и принципов теории ис­следования операций и методов теории управления с возможностями современной вычислительной техники. В настоящее время используются следующие понятия: “системный анализ”, “теория систем” и “системный подход”. Слово система и связанные с ним термины получили широкое распространение. Это произошло потому, что на передний план все более и более выступает необходимость изучения сложных комплексов (систем). Такая необходимость определяется усложнением создаваемых технических конструкций, устройств, технологий и всех совокупностей хозяйственных связей, с которыми приходится иметь дело экономистам, хозяйственным руководителям и инженерам.

Потребность изучения биологических объектов и проблем экологии, которые с каждым годом становятся все актуальнее, также приводит исследователя к сложным системам.

Понятие система относится к числу тех, для которых трудно дать строгое определение. Часто системой называют совокупность элементов, между которыми существуют те или другие связи (например система двух притягивающихся масс). Мы не будем пытаться давать строгое определение системы. Для наших целей достаточно того интуитивного поня­тия системы, которое имеется у каждого, изучающего инженерные дисциплины.

В ответ на потребности изучения сложных систем возникла дисциплина “системный анализ”. Одной из центральных проблем системного анализа является проблема принятия решений. Инструмента теории исследования операций для этих целей часто оказывается недостаточно. Как уже было сказано выше, неопределенность цели в задачах оптимизации состоит в многокритериальности. Трудно соизмерить и сопоставить между собой различные требования - трудно формализовать понятие “цель”, объединить показатели. В ряде задач либо вообще нельзя сколько-нибудь точно поставить цели, либо те цели, которые хотелось бы поставить, нереальны (примеры подобных ситуаций дает порой экономика). В таких случаях на помощь приходит системный анализ.

Допустим, что речь идет о планах перспективного развития топливно-энергетического комплекса. Как определить цели? Конечно, всегда можно сформулировать требования: топлива побольше, затрат поменьше и т.д. Но для проекта плана необходимы более или менее точные показатели и реалистические цели, которые согласуются с потребностями страны и могут быть обеспечены существующими ресурсами. В таких проблемах самый главный момент - сформулировать цели, которые должен преследовать проект. Цель перестает быть внешним фактором, как, например, в теории исследования операций или теории управления, она становится самостоятельным объектом исследования.

Что надо исследователю для того, чтобы установить (правильно сформулировать) те реальные цели, осуществление которых должны обеспечивать создаваемые конструкция или хозяйственный комплекс? Очевидно, что для этого необходимо, прежде всего, представить себе функционирование будущей конструкции, сопоставить ее возможности с теми ресурсами, которыми будут располагать разработчики. Достичь этого можно с помощью физических (макеты будущих конструкций) или математических моделей.

Таким образом, чтобы использовать математику, сначала необходимо описать систему моделей и создать математический аппарат, который позволит провести анализ изучаемого процесса, увидеть последствия принятых решений, оценить возможности при различных альтернативах, и только на основе такого анализа можно сформулировать цели. Сложность изучаемых и проектируемых систем приводит к необходимости создания специальной техники исследования, использующей аппарат имитации, - воспроизве­дения на ЭВМ специально организованными системами математических моделей функционирования проектируемого или изучаемого комплекса.

Последнее не означает недооценки классических методов анализа. Более того, эффективное использование имитационных систем необходимо предполагает предварительную обработку модели. Исследование динамики процесса, позволяющее увидеть перспективы и наметить цели, - это лишь один из аспектов системного анализа, может быть, и самый важный, но не исчерпывающий всего многообразия вопросов, на которые он в состоянии дать ответ. Это всего лишь первый шаг исследования. Следующая проблема состоит в том, чтобы реализовать намеченные цели, т.е. сформулировать решения, в результате выполнения которых будет обеспечено достижение этих целей (выбраны параметры создаваемых конструкции или проекта).

Среди задач, возникающих в связи с созданием соответствующих проектов, большое место занимают проблемы сочетания структурных и функциональных аспектов. Один из трудных вопросов, связанных с этим, относится к проблемам проектирования иерархической организации. Любые более или менее сложные системы всегда организованы по иерархическому принципу в связи с тем, что централизованные обработка информации и принятие решений часто бывают невозможны из-за большого объема информации, которую следует собирать и перерабатывать, из-за возникающих при этом задержек и искажений и т.д. Если речь идет о проектировании технических систем, то задача исследования систем (задача проектировщика) состоит в разработке функциональной схемы, которая может быть реализована заведомо не единственным способом, и в определении частных целей.

Значительно сложнее обстоит дело, когда речь идет о народнохозяйственных комплексах, функционирование элементов которых зависит от того, как управляют ими люди. В отличие от машины, человек всегда имеет собственные цели и интересы, и проектировщику системы уже недостаточно только формулировать цели для нижних звеньев. Необходимо еще быть уверенным, что эти цели будут достигнуты, что нижние звенья выполнят требования верхних звеньев. Для этого, в свою очередь, должен быть спроектирован специальный “механизм”, одного приказа для достижения цели бывает недостаточно. Вот почему возникает потребность в специальной теории, которая должна развивать принципы создания иерархии в управлении и методы их анализа. Теория иерархических систем, которая изучает некоторые из аспектов этой проблемы, является одной из важнейших частей системного анализа.

Таким образом, системный анализ - это дисциплина, развивающая методы проектирования сложных технических, народнохозяйственных и экологических систем. Системный анализ как дальнейшее развитие теории исследования операций и теории управления включает в себя эти дисциплины со всем арсеналом средств, развитых в их рамках.

В настоящее время сложилась некоторая условная классификация математических моделей по характеру и способу использования произвольных функций и параметров, которые они содержат. В их число входят следующие виды моделей:

1. Модели без управления, которые описывают динамические процессы (с помощью, например, дифференциальных или разностных уравнений) и не содержат свободных параметров или функций. К их числу относится большинство прогностических моделей, когда заданное начальное состояние определяет траекторию процесса. Модели такого рода могут быть и стохастическими, например, они могут содержать случайные величины и функции вида

x′ = f(x, t, ),

где x - некоторый случайный вектор с известным законом распределения. В этом случае исследуются не отдельные траектории, а их статистические свойства, например среднее значение. Модели подобного рода являются типичными для описания процессов, происходящих в неживой природе.

2. Модели, которые могут быть использованы для оптимизации некоторых действий. Например, динамический процесс, модель которого описывается уравнением вида

x′ = f(x, t, u),

где выбор функции u(t,x) находится в распоряжении какого-то субъекта. Вектор-функция u(f,x) называется управлением. Управление выбирается из условия достижения некоторой цели. Распространенный класс задач с помощью данной модели можно описать следующим образом: за время Т перевести систему из состояния

x(0) = x₀

в состояние

x(T) = x_T

так, чтобы “затраты” были минимальными, т.е.

(x, u, t)dt  min.

Ограничения x(0) = x₀, x(T) = x_T и целевую функцию в понятие модели не включают. Для одной и той же модели x′ = f(x, t, u) могут ставиться разные задачи.

3. Модели, которые могут использоваться для анализа конфликтных ситуаций. Предположим, что динамический процесс определяется действиями нескольких субъектов, в распоряжении которых имеются управления: u, v, w,... Тогда

x′ = f(x′, t, u, v, w, ...),

причем управления будут выбираться из условий вида

(x, u, v, w, ..., t)dt  min,

каждое из которых отражает вполне определенные интересы того или другого субъекта.