1. Основные сведения о матрице
 Скачать 386.85 Kb. Скачать 386.85 Kb.
|
|
1. Основные сведения о матрице. 1 Основные сведения о матрице. Матрицей размера mxn (читается m на n)называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,… Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: aij, где i - номер строки, j - номер столбца. Виды матриц. Матрица, состоящая из одной строки, называется матрицей (вектором)- строкой, а из одного столбца - матрицей (вектором)- столбцом Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n. Элементы матрицы aij, у которых номер столбца равен номеру строки называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a11, a22,…,ann. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. 2.Действия над матрицами. + - умножение на число. Свойства Сложение матриц опр. Суммой матриц A и B одинакового размера mxn наз-ся матрица C размера mxn, эл-ты кот. cij получаются по элементарным сложениям соответствующих элементов матриц А и В, т. е. сij=аij+bij, i= 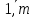 ; j= ; j=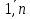 . .Вычитание матриц опр. Разность матриц А и В одинакового размера определяется через предыдущие операции как А-В=А+(-1)В, А-В=С, сij=аij-bij. зам. А+О=А; А*0=О; А*1=А Умножение матрицы на число опр. Произведением матрицы A размера mxn на число k наз-ся матрица С размера mxn, эл-ты которой получаются поэлементным умножением соответствующих элементов на число k. зам. Общий множитель всех эл-тов матрицы можно выносить за знак матрицы. 3. Действия над матрицами. Умножение м на м, транспонирование. Свойства.
опр. Произведение матрицы A размера mxk на матрицу B размера kxn наз-ся матрица C размера mxn, каждый эл-т кот. cij получается в виде произведения i-ой строки матрицы A на j-й столбец матрицы B (произведение берется как скалярное произведение i-ой вектор-строки матрицы A на j-й вектор-столбец матрицы B), т.е. cij=ai1b1j+ai2b2j+…+aikbkj. зам. Произведение матриц сущ. тогда и только тогда, когда число столбцов первой матрицы совпадает с числом строк второй. Свойства операций: AB≠BA. AE=EA=A АВ=0, из этого не следует, что А=0, В=0
опр. Транспонирование матрицы – переход от матрицы А к матрице АТ (или А’), в кот. строки и столбцы поменялись местами с сохранением порядка, при этом матрица АТ называется транспонированной относительно матрицы А, а ее эл-ты вычисляются по формуле: aTij=aji, i= 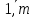 ; j= ; j=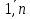 Св-ва: (AT)T=A (kA)T=kAT (A+B)T=AT+BT (AB)=BTAT Специфические свойства матриц: a) АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать. b) АВ и ВА существуют, то они могут быть матрицами разных размеров. 4. Определитель матрицы 2ого и 3ого порядка и его свойства. К каждой ква-ой матрице А , ставится в соответствие числовая характеристика, называемая ее определителем. ) Определителем первого порядка ∆1 для матрицы А размера 1х1 А=(а), называется число А. 2) Определителем второго порядка ∆2 для квадратной матрицы 2х2 А= 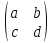 , называется число аd-bc. , называется число аd-bc.А*= 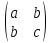 ∆2=ac-b2 ∆2=ac-b23) Определителем третьего порядка ∆3 для квадратной матрицы А= 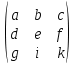 называется числовая хар-ка: aek+bfg+dik-(ceg+dbk+aif). называется числовая хар-ка: aek+bfg+dik-(ceg+dbk+aif).Св-ва определителей: 1)Величина определителя не изменится, если его строки и столбцы поменять местами, т. е. ∆(А)= ∆(АТ) 2)Перестановка двух строк (столбцов) определителя равносильна умножению определителя на (-1). 3)Если определитель имеет две одинаковые строки (столбца), то он равен нулю. 4)Умножение всех эл-тов одной строки (столбца) определителя на любое число c равносильно умножению определителя на это число c. Поэтому общий множитель всех эл-тов строки (столбца) определителя можно выносить за знак определителя. 5)Если все эл-ты строки (столбца) определителя равны 0, то он тоже равен 0. 6)Если эл-ты двух строк (столбцов) определителя пропорциональны, то он равен 0. 7)Если к эл-там некоторой строки (столбца) определителя прибавить соотв. эл-ты др. строки (столбца), умноженные на любой общий множитель, то величина определителя не изменится. 8)Определитель произведения двух квадратных матриц равен произведению их определителей. |А*В|=|А|*|В| 9)Если каждый эл-т k-го столбца (строки) определителя представляет собой сумму двух слагаемых, то исходный определитель может быть представлен в виде суммы трех определителей, из кот. один в k-том столбце (строке) имеет первые из упомянутых слагаемых, а другой вторые; а эл-ты, стоящие на остальных местах одинаковые из всех трех определителей. 5. Свойства определителя n-ого порядка. Вычисление методом приведения к треугольному виду. Определителем n-ого порядка ∆n квадратной матрицы A наз-ся число, равное алгебраической сумме n!=1·2·3·…·n слагаемых, каждое из кот. является произведением n эл-тов матрицы, взятых по одному из каждой строки и каждого столбца. Свойство. С ростом числа n увеличивается число слагаемых. Свойство. Один из способов вычисления определителя n-ого порядка – это способ приведения определителя к верхнему треугольному виду путем использования св-в определителя. Треугольный вид. Метод основан на использовании свойств определителя. Приведем матрицу к виду, когда все элементы под главной диагональю = 0. Такой определитель имеет верхний треугольный вид и он = произведению элементов на главной диагонали. 6. Свойства определителя n-ого порядка. Вычисление разложения по строке или столбцу. Определителем n-ого порядка ∆n квадратной матрицы A наз-ся число, равное алгебраической сумме n!=1·2·3·…·n слагаемых, каждое из кот. является произведением n эл-тов матрицы, взятых по одному из каждой строки и каждого столбца. Свойство. С ростом числа n увеличивается число слагаемых. Свойство. Один из способов вычисления определителя n-ого порядка – это способ приведения определителя к верхнему треугольному виду путем использования св-в определителя. Теорема о разложении определителя по строке или столбцу опр. Минором Mij эл-та aij определителя ∆n наз-ся определитель (n-1)-го порядка, т. е. ∆n-1, получаемый из исходного определителя вычеркиванием i-ой строки и j-ого столбца. опр. Алгебраическим дополнением Aij для эл-та aij определителя ∆ наз-ся число Aij=(-1)i+j*Mij. Теорема1. Определитель ∆n равен сумме произведений эл-тов любой строки на их алгебраические дополнения. ∆n=ak1Ak1+ak2Ak2+…+aknAkn для всех k= 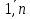 – разложение определителя по k-ой строке. – разложение определителя по k-ой строке.Теорема2. Определитель n-ного порядка равен сумме произведений эл-тов любого столбца на их алгебраические дополнения, т. е. ∆n=a1kA1k+a2kA2k+…+ankAnk – формула разложения определителя по k-ому столбцу. 7. Обратная матрица и ее свойства. Нахождение методом Гаусса. Обратная матрица. Матрицей, обратной матрице А, называется матрица A-1 такая, что A-1A = A A-1 = E. Матрица А называется невырожденной, если ΔА ≠0, а если ΔА =0 матрица называется вырожденной или особенной. А^-1называется обратной матрицей матрицы А, если Ав-1*А=А*Ав-1=Е Замечание1. Обратная матрица существует только для квадратных матриц и является квадратной матрицей n-ого порядка. Замечание 2. Обратная матрица сущ. только для невырожденных матриц. Теорема. (Необходимое и достаточное условие для сущ. Обратной матрицы) Обратная матрица существует тогда и только тогда, когда ΔА ≠0 Свойства: 1. ∆(A-1)=1/∆(A) 2. (A-1)-1=A 3. (AB)-1=B-1*A-1 4. (Am)-1 =(A-1)m Метод Гаусса. Преобразование строк, которые переводят исходную матрицу А в равносильную ей матрицу. 2 действия: 1-умножение всех элементов строки на число неравное 0 2-прибавление к j-строке k-строке умноженного на число С Метод. К матрице А приписывается матрица Е. (А/Е) называется это расширенной матрицей. После элементарных преобразований строк полученной матрицы ее необходимо привести к виду (Е/В), тогда В и будет обратной матрицей. 8. Обратная матрица и ее свойства. Нахождение методом алгебраических дополнений. Обратная матрица. Матрицей, обратной матрице А, называется матрица A-1 такая, что A-1A = A A-1 = E. Матрица А называется невырожденной, если ΔА ≠0, а если ΔА =0 матрица называется вырожденной или особенной. А^-1называется обратной матрицей матрицы А, если Ав-1*А=А*Ав-1=Е Замечание1. Обратная матрица существует только для квадратных матриц и является квадратной матрицей n-ого порядка. Замечание 2. Обратная матрица сущ. только для невырожденных матриц. Теорема. (Необходимое и достаточное условие для сущ. Обратной матрицы) Обратная матрица существует тогда и только тогда, когда ΔА ≠0 Свойства: 1. ∆(A-1)=1/∆(A) 2. (A-1)-1=A 3. (AB)-1=B-1*A-1 4. (Am)-1 =(A-1)m Метод алгебраических дополнений. 9. Понятие СЛУ. опр. Системой m линейных уравнений с n неизвестными наз-ся система a11x1+a12x2+…+a1jxj+…+a1nxn=b1} a21x1+a22x2+…+a2jxj+…+a2nxn=b2} (*) ai1x1+ai2x2+…+aijxj+…+ainxn=bi} am1x1+am2x2+…+amjxj+…+amnxn=bm}, где aij i=1,m; j=1,n – коэффициенты при неизвестных, bi – свободные числа. опр. Решение системы (*) – совокупность n чисел (k1,k2,…,kn) при подстановке кот. каждое ур-ние системы обращается в верное равенство. опр. Решить систему (*) – найти все ее решения или убедиться, что их нет. опр. Система (*) – совместная, если она имеет хотя бы одно решение. Система (*) – несовместная, если она не имеет решений. опр. Совместная система (*) наз-ся определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения. А*Х=b – матричная форма записи (*). опр. Две системы линейных ур-ний (СЛУ) наз-ся равносильными (эквивалентными), если они имеют одно и то же множество решений, т.е. если 1)обе совместны и имеют одни и те же решения; 2)обе несовместны. опр. Система (*) – однородная, если все bi=0, в противном случае – неоднородной. зам.Однородные системы всегда совместны. Решение (0;0;0…0) – нулевое или тривиальное. 10.Решение системы линейных уравнений в матричной форме. А*Х=b: рассмотрим систему (*) a11x1+a12x2+…+a1jxj+…+a1nxn=b1} a21x1+a22x2+…+a2jxj+…+a2nxn=b2} (*) ai1x1+ai2x2+…+aijxj+…+ainxn=bi} am1x1+am2x2+…+amjxj+…+amnxn=bm} в матричной форме. Пусть m=n и ∆А ≠0. Тогда сущ. A-1. Домножим обе части ур-я на A-1 слева: A-1*АХ=A-1*b ЕХ=A-1*b Х= A-1*b – решение ур-я. 11. Метод Крамера решения систем линейных уравнений. 12. Метод Гаусса решения систем линейных уравнений: случай треугольного вида. ---- 13. Метод Гаусса Решение СЛУ: случай вида трапеции. --- 14. Однородные системы линейных уравнений. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: 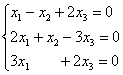 Однородная система всегда совместна, то есть всегда имеет решение. Если ранг матрицы системы равен количеству переменных, то однородная система линейных уравнений имеет только тривиальное решение. 15. Собственные вектора матрицы. Собственные значения матрицы. Определение: ненулевой вектор Число 16. Понятие n-мерного вектора. Основные определения. Упорядоченная совокупность n действительных или комплексных чисел Числа Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках. Если записать вектор a как 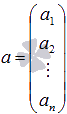 , то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора. , то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора. Вектор Вектор 17. Операции над векторами, основные свойства операции. Для n-мерных векторов задаются две операции: сложение векторов и умножение вектора на число Суммой двух векторов Следует отметить, что складывать можно только векторы количество координат, которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена. Произведением действительного или комплексного числа Свойства операций над n-мерными векторами. Для любых векторов -свойство коммутативности сложения векторов a+b=b+a; -свойство ассоциативности векторов (a+b)+c=a+(b+c); -существует нейтральный вектор по операции сложения, им является нулевой вектор, a+0=a; -для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a+(-a)=0; -Сочетательное свойство умножения -Первое распределительное свойство -Второе распределительное свойство -существует нейтральное число по операции умножения, им является единица Эти свойства справедливы в силу свойств операций сложения и умножения действительных или комплексных чисел. Операции вычитания векторов как таковой нет, так как разность векторов a и b есть сумма векторов a и -b. 18. Линейная зависимость и независимость системы векторов. Если линейная комбинация Если линейная комбинация Свойства линейной зависимости и линейной независимости системы векторов.
19. Базис и ранг системы векторов. Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов Существенным моментом определения является тот факт, что векторы взяты в определённом порядке. Базисы Рангом квадратичной формы (2) называется ранг её матрицы 20. Понятие квадратичной формы. Стандартный канонический вид. Критерий знакоопределенности. Квадратичной формой Говорят, что квадратичная форма имеет канонический вид, если она содержит только квадраты переменных и не содержит парных произведений разноименных переменных: 21. Понятие экономико-математической модели и задачи линейного программирования. Экономико-математическая модель – совокупность формул, описывающая процессы, происходящие в реальном экономическом процессе. Принципы построения ЭММ: 1) Принцип достаточности исходной информации; 2) Принцип однозначности информации; 3) Принцип преемственности; 4) Принцип эффективности. Задача линейного программирования (ЗЛП) – простейший пример ЭММ. ЭММ – математическое описание исследуемого эк. процесса или объекта, выражающее закономерности эк. процесса в абстрактном виде с помощью математич. соотношений, что позволяет углубить колич. математич. анализ, расширить область эк. информации, интенсифицировать эк. расчет. 3 этапа построения ЭММ: а) постановка цели, задачи исследования, качественное описание объекта в виде эк. модели; б) построение математ. модели изучаемого объекта, выбор (разработка) методов исследования, подготовка исходной инфы, реализация модели на ЭВМ; в) анализ матем. модели, обработка полученных результатов. 22. Задачи планирования производства: общий вид, пример. Задача планирования производства содержательно ставится следующим образом. Пусть имеется некоторый экономический объект (предприятие, цех, артель и т. п.). Необходимо спланировать производство n видов продукции, если известно:
Требуется составить оптимальный план производства продукции, то есть такой план, который максимизирует суммарную прибыль от реализации всей произведенной продукции и при этом не происходит перерасхода ресурсов. 23. Задача о рационе (диете, смесях и сплавх) общий вид и пример. Имеется n видов продуктов питания и m химических элементов, необходимых для суточного потребления. aij – содержание i-го (i=1,2,…,m) химического элемента в одной единице j-го (j=1,2,…,n) продукта питания. bi – минимальное суточное потребление i-го химического элемента. cj – стоимость одной единицы j-го продукта питания. Требуется составить суточный рацион питания – сколько продуктов каждого вида нужно приобрести, чтобы рацион имел минимальную стоимость, и питание было разнообразным. В задаче о диете стоимость можно заменить на калорийность продуктов питания, и сформулировать задачу в следующем виде: питание должно быть низкокалорийным, но содержать все необходимые для суточного потребления химические элементы. Строим экономико-математическую модель. Управляемая переменная xj – количество продукта j-го вида, которое будем приобретать (j=1,2,…,n). Функция цели – суммарная стоимость продуктов питания Ограничения 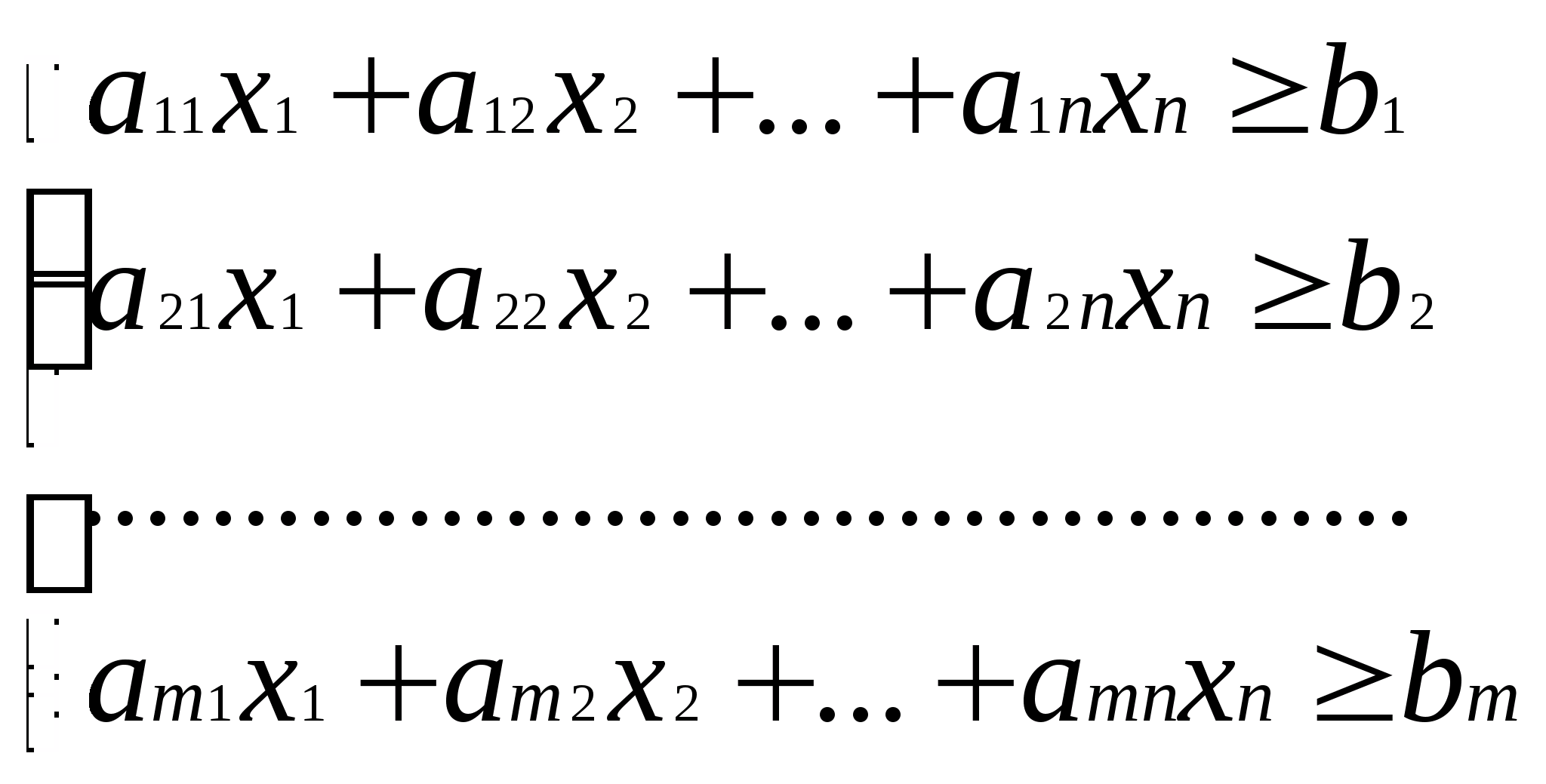 (2) (2)xj 0, j=1,2,…,n (3) Решить задачу – значит найти вектор Эта задача также является задачей линейного программирования. Можно формально свести эту задачу к предыдущей, если вместо минимизации функции 24. Общая постановка задачи линейного программирования. Стандартная и каноническая задача линейного программирования. Общая постановка задачи линейного программирования (ЗЛП) Найти вектор 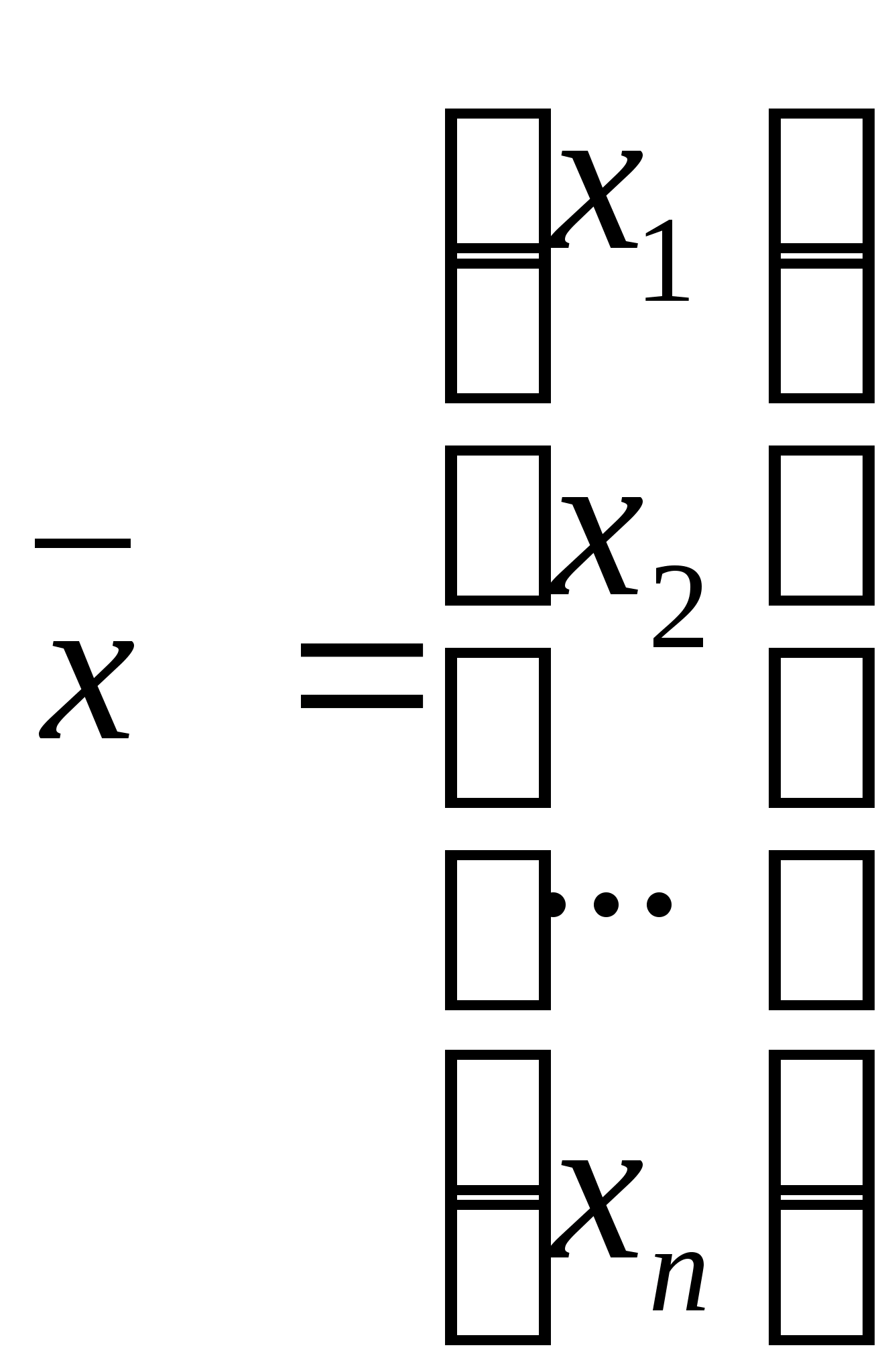 пространства En который максимизирует (минимизирует) функцию цели пространства En который максимизирует (минимизирует) функцию цели при следующих условиях 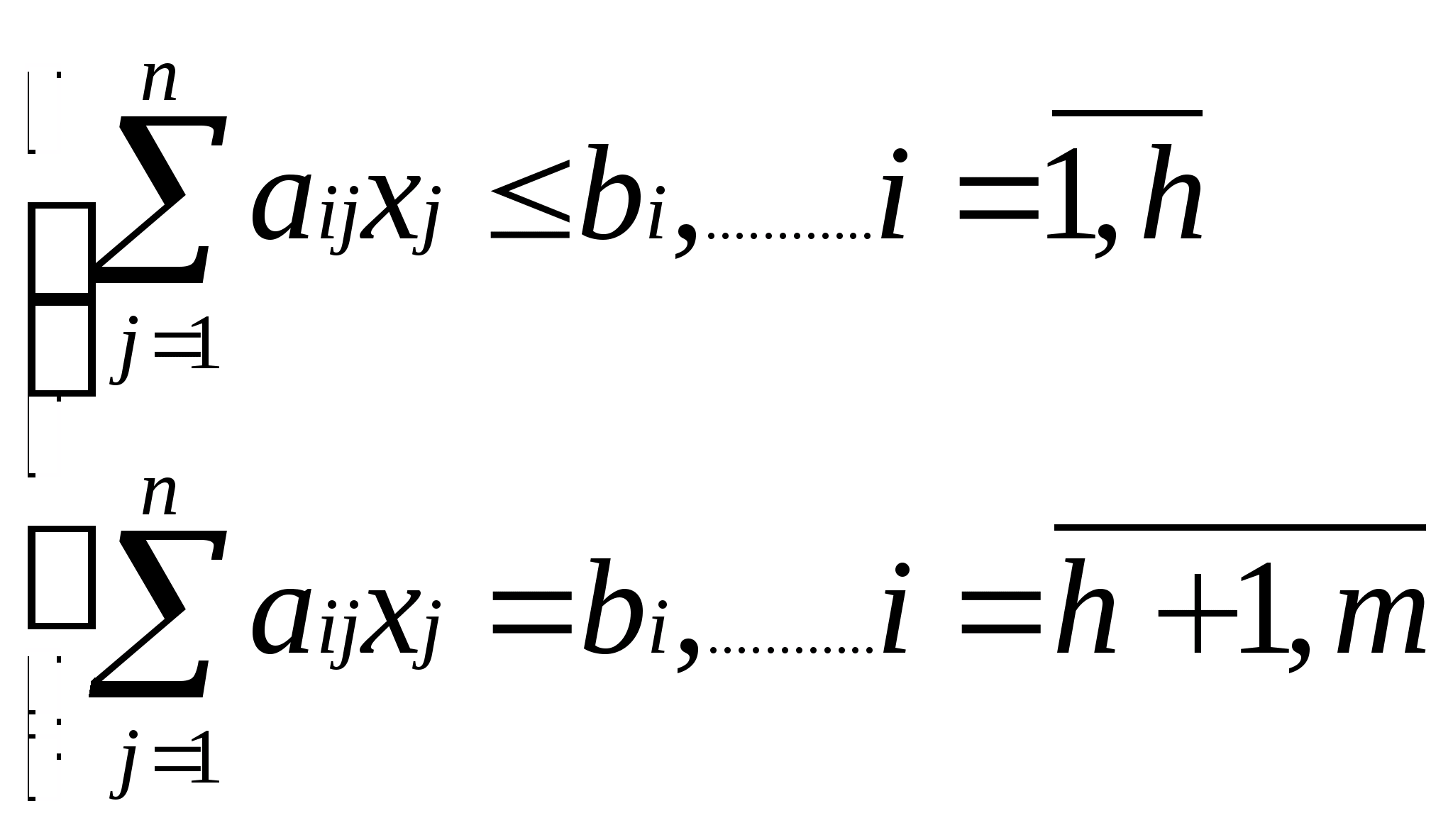 (2) (2)x1,x2,…,xp≤0, (p≤n) (3)
Условимся относительно терминологии, которую будем использовать в дальнейшем. Вектор Множество всех планов ЗЛП называется областью допустимых планов ЗЛП и обозначается ОДП. Решение ЗЛП находится на границе области ОДП. Оптимальным планом ЗЛП (решением ЗЛП) называется такой план Каноническая задача линейного программирования (КЗЛП) Канонической задачей линейного программирования называют следующую задачу: Найти вектор 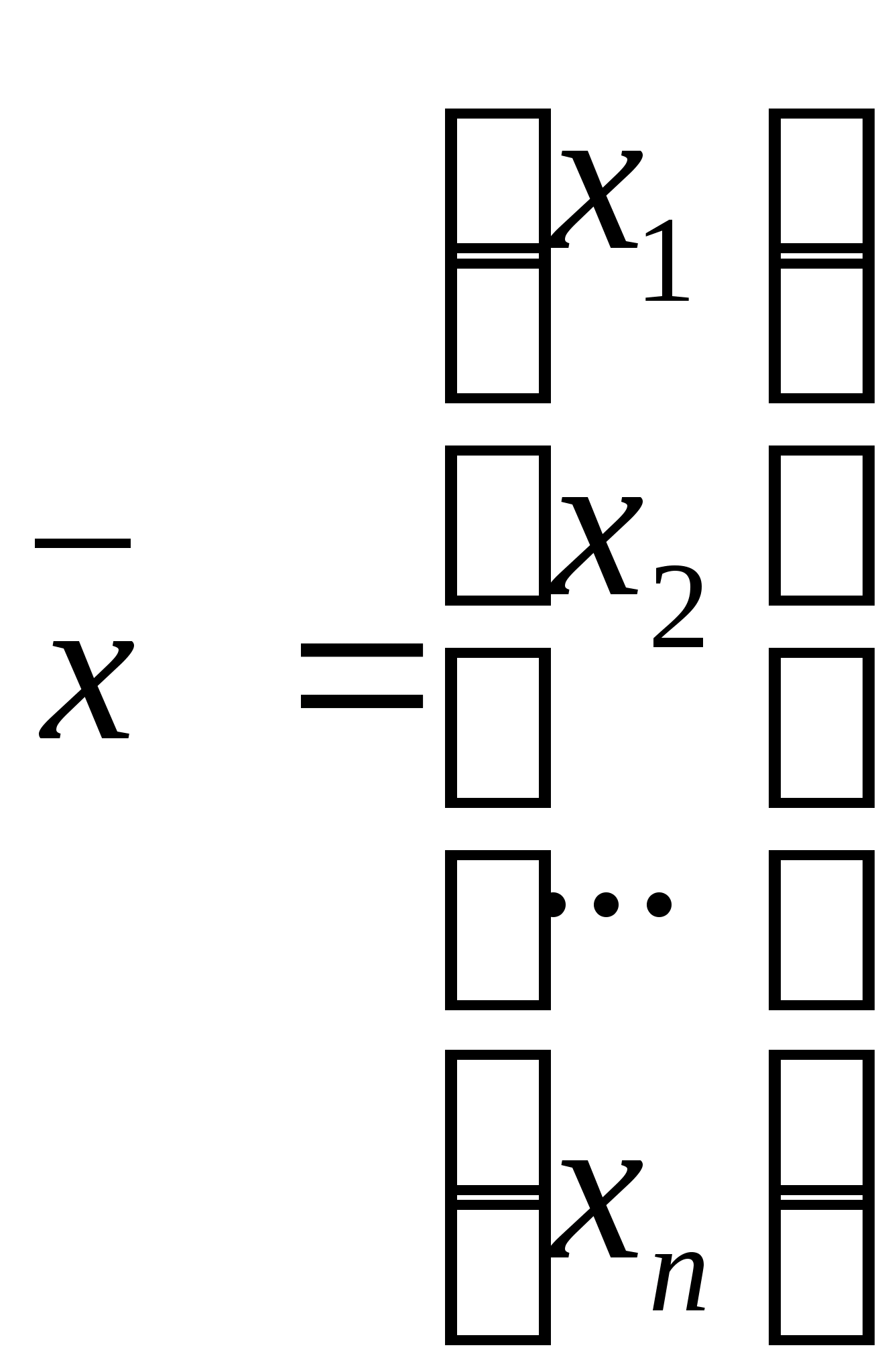 пространства En который максимизирует функцию цели пространства En который максимизирует функцию цели при следующих условиях 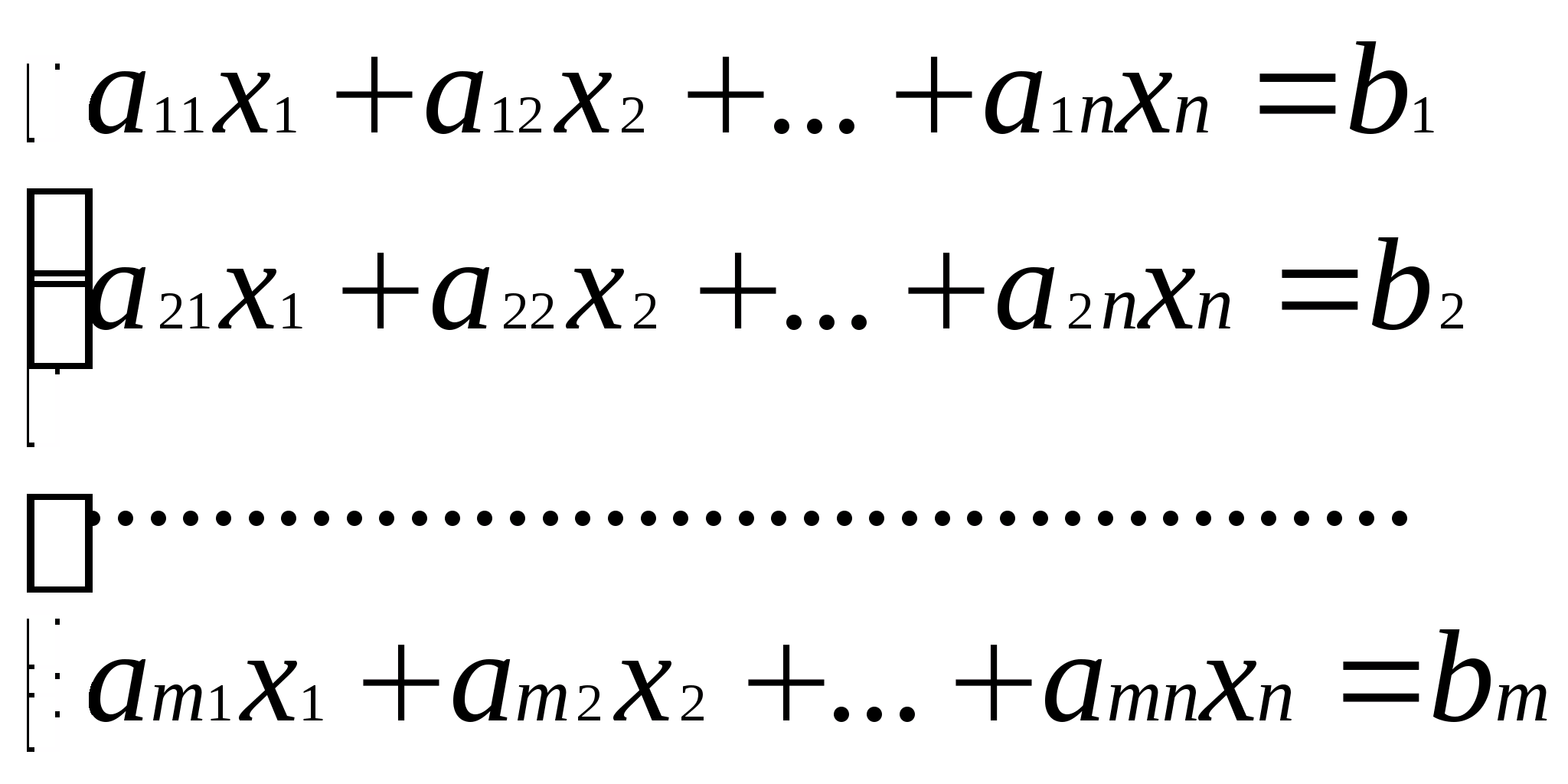 (2) (2)x1,x2,…,xn≥0 (3) 25. Графическое решение задачи линейного программирования на примере. F=2х1+3х2max} х1+3х218} 2х1+х216} х25} 3 х121} х1, х2≥0} Построение допустимого множества решений. Т. к. х1, х2≥0, то рассматривается I координатная четверть. OABCDE – допустимое множество решений; О(0;0); А(0,5); Е(7,0); В(3,5); D(7,2); С(6,4). Каждое неравенство системы задает на плоскости полуплоскость. При решении системы на плоскости получается некоторое множество – допустимое множество решений. aх1+bх2c aх1+bх2=c – определяющая прямая х1 0? х2 ?0 М – производная точка, проверяются ее координаты в неравенство. х1+3х218 х1+3х2=18 х1 0 18 6 х2 6 0 4 М(1,1)-уд. 2х1+х216 2х1+х2=16 х1 0 8 6 х2 16 0 4 М(2,2)-уд. х25 3 х121 х17 Построение вектора-градиента к линии уровней для целевой ф-ции. F=F(х1,х2); F= 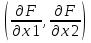 F=F(х1,х2)=с1х1+с2х2 grad F = (c1,c2) grad F = (x1,x2) F(х1,х2)=const – линия уровней 2х1+3х2=с 2х1+3х2=0} 2х1+3х2=6} 2х1+3х2=-12} … Это бесконечной семейство параллельных друг другу прямых. Всё семейство перпендикулярно вектору-градиенту. Нахождение оптимального решения Оптимальная точка – одна из точек-вершин многоугольника OABCDE. Оптимальная точка – точка последнего касания линии уравнений в направлении вектора-градиента. Fmax=F(c)=F(6,4)=12+12=24. Таким образом, необходимо выпустить р1 в кол-ве 6 ед., р2 в кол-ве 4 ед., при этом суммарная прибыль = 24. |
