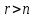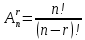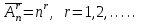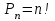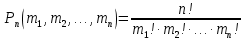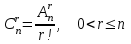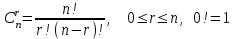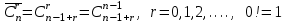Практичне заняття. 1 ПРАКТИЧНЕ ЗАНЯТТЯ. 1 практичне заняття 1
 Скачать 97.7 Kb. Скачать 97.7 Kb.
|
|
1 ПРАКТИЧНЕ ЗАНЯТТЯ № 1. ОСНОВНІ ПОНЯТТЯ КОМБІНАТОРИКИ. ФОРМУЛИ ДОДАВАННЯ І МНОЖЕННЯ ЙМОВІРНОСТЕЙ. 1.1 Мета заняття Закріпи на практиці навички використання основних формул комбінаторики, додавання та множення ймовірностей для розв'язання задач. 1.2 Теоретичні відомості 1.2.1 Основи комбінаторики. Класична ймовірність. У своїй практичній діяльності ми часто зустрічаємося з явищами, результат яких неможливо передбачити, бо він залежить від випадку. Теорія ймовірностей – це розділ математики, в якому вивчаються випадкові явища (події) і виявляються закономірності при масовому їх повторенні. Основне поняття теорії ймовірностей – ймовірність події (відносна частота події) – об'єктивна міра можливості здійснення даної події. Подія – це явище, про яке можна сказати, що воно відбувається чи не відбувається за певних умов. Події прийнято позначати великими літерами латинського алфавіту: А, В, С, D. Будь-яка подія відбувається внаслідок випробування (експерименту, досліду). Випробування – це умови, за яких відбувається (чи не відбувається) подія. Перелічимо основні види випадкових подій: події називаються несумісними, якщо ніякі дві з них не можуть відбутися в даному випробуванні (експерименті) разом. Наприклад, при підкиданні монети поява цифри виключає одночасну появу герба; дві події називаються сумісними, якщо поява однієї з них не виключає появу іншої події в тому ж випробуванні (експерименті); подія називається достовірною, якщо вона відбувається в даному випробуванні обов'язково. Наприклад, виграш по квитку безпрограшної лотереї є подія достовірна; подія називається неможливою, якщо вона в даному випробуванні не може відбутися. Наприклад, при киданні гральної кістки неможливо отримати 7 очок; дві події називаються протилежними (А і А̄), якщо в даному випробуванні вони несумісні і одна з них обов'язково відбувається. Ймовірності протилежних подій в сумі дають 1; подія В називається незалежною від події А, якщо поява події А не змінює ймовірності події В: Р(A|В)=Р(В). В іншому випадку подія В називається залежною від події А. Повної системою подій А1, А2, А3, ..., Аn називається сукупність несумісних подій, настання хоча б однієї з яких обов'язково при цьому випробуванні (експерименті). Кожній події A ставиться у відповідність деяка міра P(A), яка називається ймовірністю цієї події і яка задовольняє наступним аксіомам: для будь-якої події 0 ≤ P(A) ≤ 1; ймовірність неможливої події дорівнює нулю, P(А) = 0; ймовірність достовірної події дорівнює одиниці, Р(А) = 1. Існує класичний і геометричний способи підрахунку ймовірності події. При класичному способі підрахунку ймовірність події А обчислюється за формулою:
де: всі елементарні результати є рівноможливими, тобто жоден з них не є більш можливим, ніж інший; m – число елементарних результатів випробування, що сприяють появі події А; n – загальне число всіх можливих елементарних фіналів випробування. Приклад 1. Кинули монету один раз. Яким є шанс того, що вона впаде гербом (орлом) угору? Розв'язання. Кидання монети є випадковим дослідом (його можна повторити багато разів за однакових умов при неможливості передбачити результат заздалегідь), тоді випадання герба є випадковою подією. Скільки може бути варіантів того, що монета ляже вгору гербом чи цифрою, якщо вважати неможливим, що монета стане на ребро? У монети дві сторони. І якщо вона симетрична, то шанси того, що вона впаде на кожну з них, однакові. Отже, шанси дорівнюють ½, або 50%. Відповідь: ½, або 50%. Задачі для тренування. Задача 1. Підкинули дві монети. Які шанси того, що обидві монети упадуть гербом угору? (1/4 чи 25%) Задача 2. Чому дорівнює ймовірність випадання п'яти очок при одному підкиданні грального кубика? (1/6) Задача 3. Якою є ймовірність витягнути пікового туза при витягування однієї карти з колоди 36 карт? (1/36) Для підрахунку n і m часто застосовуються поняття і формули комбінаторики. Розміщеннями без повторень або просто розміщеннями з n елементів множини B по r елементів будемо називати всілякі впорядковані підмножини B, що містять r різних елементів множини B. Число розміщень з n по r (формула 2) :
Загалом використовується наступна формула (3):
Приклад 2. У пасажирському поїзді 9 вагонів. Скількома способами можна розсадити у поїзді 4 людини при умові, що вони повинні їхати у різних вагонах? Розв'язання. Кількість можливих розміщень з n=9 різних елементів по m=4 можна визначити через розміщення з 9 по 4 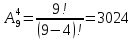 Відповідь: 3024 Приклад 3. Скільки тризначних чисел можна записати цифрами 0, 1, 2, 3, 4, якщо кожну з цих цифр можна використовувати не більше одного разу? Розв'язання. Згідно теорії, кількість можливих розміщень з n=5 різних цифр по m=3 без повторень можна визначити за формулою розміщень: 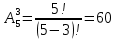 Відповідь:60 Так обчислить практично більшість студентів і допустить одну з поширених на практиці помилок. Справа в тому, що цифра 0 не може бути на початку число. І не важливо чи число двозначне, тризначне чи ще більше. Це одна з поширених хитрощів на якій Вас можуть підловити викладачі. Правильну відповідь на запитання можна отримати з наступних міркувань: На перше місце можна поставити одну з чотирьох цифр (1, 2, 3, 4), нехай це буде 4. Відповідно на друге місце можна вибрати одну цифру з наступних (0, 1, 2, 3), оскільки значення не повинні повторюватися. Візьмемо для прикладу 0. На 3 позицію в числі можна поставити 1 з 3 цифр (1,2,3), нехай це буде 3. Таким чином ми дістали 403. Загальне значення це добуток всіх варіантів в кожному пункті, а саме: 1 з 4 для 1 цифри, 1 з 4 для 2; 3 для третьої. За правилом добутку отримаємо N=4·4·3=48. Це значення менше ніж помилково знайдене 60. Завжди в задачах де маєте сумніви користуйтеся логічними висновками в противагу формулам ймовірності. Вони мають широке застосування, однак в ряді випадків дають неправильне значення через ваше небажання краще дослідити умову прикладу. Задачі для тренування. Задача 1. Скільки можна скласти сигналів з 6 прапорців різного кольору, взятих по 2? (30) Задача 2. У пасажирському поїзді 9 вагонів. Скількома способами можна розсадити у поїзді 4 людини при умові, що вони повинні їхати у різних вагонах? (3024) Задача 3. У першості школи з шахів беруть участь 15 учнів. Скількома способами можуть бути розподілені призові місця? (2730) Розміщеннями з повтореннями з n елементів множини B по r елементів, будемо називати впорядковані набори по r елементів множини B, серед яких можуть бути й однакові елементи. Число таких розміщень дорівнює (формула 4):
Приклад 4. Вздовж дороги розташовані 6 світлофорів, кожен з яких має 3 стани: "червоний", "жовтий", "зелений". Скільки може бути різних ситуацій на дорозі, що спричинені станами цих світлофорів? Розв'язання. Напишемо декілька комбінацій: ЧЧЖЗЗЧ, ЖЖЖЖЖЖ, ЗЖЖЗЧЧ... Ми бачимо, що склад вибірки змінюється і порядок елементів істотний (адже якщо, наприклад, у вибірці ЧЧЖЗЗЧ поміняти місцями Ж і З, ситуація на дорозі буде іншою). Тому застосовуємо формулу розміщень з повтореннями з 3 по 6: 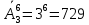 Відповідь: 729 Задачі для тренування. Задача 1. Скількома способами кур'єрською поштою можна надіслати 6 листів, якщо для цього задіяти трьох кур'єрів і кожного листа можна дати кожному з них? (729) Задача 2. Скільки чотирилітерних "слів" можна скласти з літер "М" і "А"? (16) Задача 3. Шість ящиків з будівельними матеріалами доставляються на п'ять поверхів будівлі. Скількома способами можна розподілити ящики по поверхах будівлі? (15625) Перестановками з n елементів множини B назвемо розміщення з n елементів множини B по n елементів. Число перестановок з n різних елементів дорівнює:
Приклад 5. Олександр, Іван, Петро, Денис, Оля та Настя часто ходять в кафе. Кожен раз, обідаючи там, вони розсаджуються по різному. Скільки днів друзі можуть це робити без повтору ? Розв'язання. 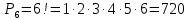 Відповідь: 720 днів (приблизно 2 роки!!!) Задачі для тренування. Задача 1. Десять чоловік сідають за круглий стіл. Два розміщення по місцях будемо вважати однаковими, якщо кожна людина має одних і тих самих сусідів в обох випадках. Скільки існує способів сісти за стіл? (181440) Задача 2. Скількома способами можна посадити за круглий стіл 5 чоловік і 5 жінок так, щоб ніякі дві особи однієї статі не сиділи поряд? (28800) Задача 3. На книжній полці 10 книжок. Скількома способами можна переставити книги так, щоб 3 виділені книги були поряд в будь-якому порядку? (241920) Перестановки з повтореннями. Розміщення з повтореннями, що відрізняються лише порядком елементів у них, називають перестановками з повтореннями. Тобто це вибірки виду (а1, а2,...,аn), де елемент а1 зустрічається m1 разів, елемент а2 – m2 разів, елемент аn – mn разів. Тоді довжина всієї вибірки буде дорівнювати (формула 6)
Набір натуральних чисел (m1, m2, …, mn) називають складом цієї вибірки. Наприклад, (А, А, С, В, А, С) – вибірка складу (3, 1, 2) із множини, що містить три елементи {А, В, С}. Кількість таких вибірок одного і того самого складу називають кількістю перестановок з повтореннями з n елементів із заданими числами повторень m1, m2, ..., mn кожного елемента. Це число позначають через Pn(m1, m2, …, mn) і обчислюють за формулою 7:
де n=m1+m2+…+mn Приклад 6. Скількома способами можна розташувати білі фігури: 2 коней, 2 слонів, 2 тур, 1 ферзя і 1 короля на першій лінії шахової дошки? Розв'язання. Потрібно обчислити кількість упорядкованих вибірок довжиною 8, які мають заданий склад (2, 2, 2, 1, 1), тобто кількість перестановок з повтореннями: 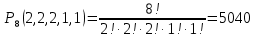 Відповідь: 5040 Задачі для тренування. Задача 1. Скільки різних слів можна отримати, переставляючи букви в слові «Міссісіпі»? (2520) Задача 2. Скільки різних браслетів можна зробити з 5 смарагдів, 6 рубінів і 7 сапфірів (всі камені одного виду однакові), якщо в браслет входять усі 18 каменів? (14702688) Задача 3. У мами 2 яблука, 3 груші і 4 апельсини. Кожний день вона дає дочці по одному фрукту. Скількома різними способами це можна зробити? (1260) Сполученнями (комбінації) з n елементів множини B по r елементів назвемо підмножину множини В, що містить r різних елементів множини В. Число сполучень з n по r дорівнює (формули 8 та 9):
або
Приклад 7. Скількома можливими способами можна вибрати з 15 людей делегацію в складі 3 осіб. Розв'язання. Шукане число (кількість можливих вибірок) є числом сполучень із 15 по 3: 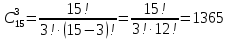 Відповідь: 1365 Задачі для тренування. Задача 1. Скільки є можливих способів для утворення дозору з трьох солдатів та одного офіцера, якщо є 80 солдат і 3 офіцери? (246480) Задача 2. Знайти число діагоналей опуклого десятикутника. (35) Задача 3. Скількома способами можна вибрати дві деталі із ящика, що містить 10 деталей? (45) Сполучення (комбінації)з повтореннями з n елементів множини B по r елементів, назвемо всілякі набори, що містять r елементів множини В, серед яких можуть бути однакові. Число сполучень з повтореннями з n по r дорівнює (формули 10 та 11):
або
Приклад 8. Скільки існує різних кидань двох однакових кубиків? Розв'язання. Усього при підкиданні одного кубика можливі шість ситуацій – маємо предмети шести різних типів. Підкидають два кубики, отже, з даних шести типів предметів необхідно вибрати два, причому нас не цікавить порядок вибору, і допускається вибір однакових предметів. Таким чином, це задача на сполучення з повторенням. По формулі для обчислення кількості сполучень із повторенням маємо: 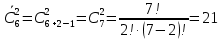 Відповідь: 21 Задачі для тренування. Задача 1. Скількома способами можна роздати десять однакових цукерок трьом дітям? (66) Задача 2. У бібліотеці є книги з 12 розділів науки: математики, фізики, інформатики тощо. Надійшли три замовлення на літературу. Вважаючи будь-який склад замовлення рівноможливим, знайти кількість способів формування замовлення. (364) Задача 3. У кондитерському магазині продавалися 4 сорти тістечок: наполеони, еклери, пісочні і листкові. Скількома способами можна купити 7 тістечок? (120) Зауваження різні розміщення з n елементів множини В по r елементів (з повтореннями і без повторень) відрізняються одне від одного складом (хоча б одним з елементів) або порядком (роль елементів в розміщенні різна); різні перестановки з n елементів множини В відрізняються одна від одної тільки порядком проходження елементів; різні сполучення з n елементів множини В по r елементів відрізняються одне від одного тільки складом. Приклад 9. Скількома способами два студента можуть з’їсти 10 пончиків, якщо кожен з них може з’їсти по 5? За схемою отримуємо: n=10, k=5, порядок не важливий, повторень немає. Потрібна формула: Сполучення 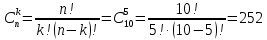 Відповідь:252 Задачі для тренування. Задача 1. Знайдіть кількість різних чотирицифрових чисел, які можна скласти з цифр 0, 3, 7, 9 (цифри в числі не повторюються). Задача 2. У деякій країні 20 міст, кожні два з яких мають авіасполучення. Скільки авіаліній у цій країні? (190) Задача 3. Студенти другого курсу згідно учбового плану вивчають 10 дисциплін. На один день можна планувати заняття з 4 дисциплін. Скількома способами можна скласти розклад занять на один день? (5040) 1.2.1. Два основні принципи комбінаторики Основне правило комбінаторики. Між скінченними множинами A та В можна встановити взаємно однозначну відповідність тоді і тільки тоді, коли вони мають однакову кількість елементів. Основне правило комбінаторики дозволяє виконувати обчислення кількості елементів множини фактично зведенням до множини з відомою кількістю елементів або до множини, для якої кількість можна підрахувати дещо простіше. У більшості випадків його використання не акцентується, а приймається як дещо зрозуміле. Значна кількість формул і теорем комбінаторики ґрунтуються на двох основних елементарних принципах, які називаються принципами суми та добутку. Принцип суми. Нехай n(A), n(B) – кількості елементів скінченних неперетинних множин А та В відповідно. Тоді для множини С = A Ս B кількість елементів обчислюється за формулою 12:
Принцип добутку. Нехай потрібно послідовно виконати k дій, причому першу дію можна виконати n1 способом, після чого другу дію – n2 способами і так далі до k-ї дії, яку можна виконати nk способами. Тоді всі k дій можна виконати 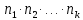 способами. способами.Розглянемо приклади обчислення класичної ймовірності за допомогою формул комбінаторики. |

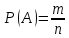
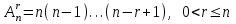
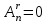 при
при