1. Предмет и задачи курса эмм, его место в системе экономических дисциплин 3
 Скачать 322.14 Kb. Скачать 322.14 Kb.
|
Задание 2Решить графическим методом задачу линейного программирования. Найти максимальное и минимальное значение целевой функции при заданных ограничениях. 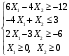 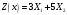 Решение: Записываем уравнения границ (прямых): 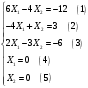 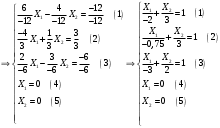 и строим их на плоскости в прямоугольной декартовой системе координат 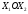    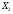 2) 1) 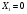     3) 3)          5 М 5 М   4 4    3 3     2 В 2 В           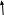  1 1   -3 -2 -0,75 А0 3 -3 -2 -0,75 А0 3 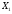 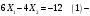 первая прямая, строим её по двум точкам первая прямая, строим её по двум точкам 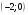 и и 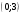 . Подставим координаты контрольной точки О(0;0) в первое неравенство . Подставим координаты контрольной точки О(0;0) в первое неравенство 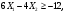 получим получим 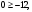 неравенство верное, следовательно, областью первого неравенства служит нижняя полуплоскость. неравенство верное, следовательно, областью первого неравенства служит нижняя полуплоскость.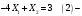 вторая прямая, строим её по двум точкам вторая прямая, строим её по двум точкам 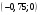 и и 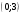 . Подставим координаты контрольной точки О(0;0) во второе неравенство . Подставим координаты контрольной точки О(0;0) во второе неравенство 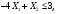 получим получим 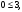 неравенство верное, следовательно, областью второго неравенства является правая полуплоскость. неравенство верное, следовательно, областью второго неравенства является правая полуплоскость.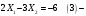 третья прямая, строим её по двум точкам третья прямая, строим её по двум точкам 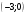 и и 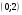 . Подставим координаты контрольной точки О(0;0) в третье неравенство . Подставим координаты контрольной точки О(0;0) в третье неравенство 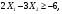 получим получим 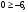 неравенство верное, следовательно, областью третьего неравенства является нижняя полуплоскость. неравенство верное, следовательно, областью третьего неравенства является нижняя полуплоскость.Неравенства 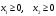 означают, что область допустимых значений будет расположена справа от оси означают, что область допустимых значений будет расположена справа от оси 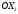 и над осью и над осью 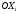 . .В результате получим бесконечную область допустимых решений, которая ограничена снизу и не ограничена сверху, Строим вектор-градиент целевой функции 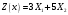 по двум точкам O0,0 и по двум точкам O0,0 и 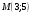 , то есть OM. , то есть OM.Проводим пунктирной линией линию уровня – любой перпендикуляр к вектору-градиенту. Max нам не найти, так как область допустимых решений не ограничена сверху. Чтобы найти min, линию уровня перемещаем в противоположном направлении вектора-градиента до тех пор, пока не достигнем последней точки выхода из области допустимых решений. Это и будет точка min целевой функции – точка А(0;0). Находим значение целевой функции Z в точке min А: 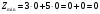 Ответ: 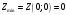 |
