1. Предмет и задачи курса эмм, его место в системе экономических дисциплин 3
 Скачать 322.14 Kb. Скачать 322.14 Kb.
|
Задание 5Разработать модель конкретной задачи (условие задачи переписывается) в числовой развернутой и матричной форме. Привести систему ограничений к канонической форме и обосновать значение дополнительных переменных. Решить задачу на ЭВМ в программе Excel «Поиск решения». Провести анализ полученного оптимального плана с помощью двойственных оценок, используя их свойства. В заключении необходимо сделать выводы о целесообразности производства в данных условиях с точки зрения рассматриваемого критерия оптимальности. При оформлении задания прикладываются распечатки исходных данных и оптимального плана, полученных на ЭВМ. Найти оптимальное сочетание посевов трех культур: пшеницы, гречихи и картофеля. Эффективность возделывания культур в расчете на 1 га характеризуются показателями, значения которых приведены в таблице. Таблица
Производственные ресурсы: 6000 га пашни, 5000 чел. – дней труда механизаторов, 9000 чел. – дней ручного труда. Производство пшеницы должно составлять не менее 6500 ц. Критерий оптимальности – максимум прибыли. Решение: Вводим управляющие переменные: 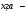 пашни засеяно пшеницей, пашни засеяно пшеницей, 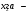 пашни засеяно гречихой, пашни засеяно гречихой, 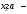 пашни засеяно картофелем. пашни засеяно картофелем. Составим систему ограничений: 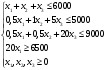 Целевая функция 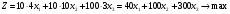 – максимум прибыли. – максимум прибыли.Приведем систему ограничений к каноническому виду: 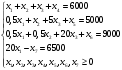 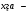 пашни осталось неиспользованным, пашни осталось неиспользованным, 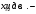 недоиспользовано труда механизаторов, недоиспользовано труда механизаторов, 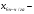 недоиспользовано трудовых ресурсов, недоиспользовано трудовых ресурсов,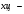 изыток производства пшеницы, изыток производства пшеницы, Решая задачу на ЭВМ в программе Excel «Поиск решения», получим:
Максимальный доход составит 496750 руб. При этом будет пшеницей засеяно 325 га пашни, гречихой 4837,5 га. Проведем анализ полученного оптимального плана с помощью двойственных оценок. В отчёте по результатам содержатся оптимальные значения переменных Х1, Х2, Х3, которые, соответственно, равны 325; 4837,5; 0; значение целевой функции – 496750, а также левые части ограничений
Отчет по устойчивости Отчёт по устойчивости приводится в виде таблицы. Первая часть таблицы содержит информацию, относящуюся к переменным: нормированная стоимость для картофеля равна 200 (строка 2). Это означает, что если мы несмотря на оптимальное решение (325; 4837,5; 0) попробуем включить в посевную 1 га картофеля, то новый план посевной будет иметь доход 496550 руб., что на 200 руб. меньше, чем полученное оптимальное решение.
предельные значения приращения целевых коэффициентов ∆сi, при которых сохраняется первоначальное оптимальное решение. Допустимое увеличение стоимости 1 ц. картофеля – 200 руб. Допустимое уменьшение – практически не ограничено. Если стоимость 1 ц. картофеля увеличится более чем на 200 руб., то оптимальное решение изменится: станет целесообразным использовать Х3. А если стоимость 1 ц. картофеля буде уменьшаться, то оптимальное решение (325; 4837,5; 0) останется прежним. Во второй части таблицы содержится информация, относящаяся к ограничениям. Рассмотрим анализ дефицитных ресурсов. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие предприятию засеивать большую площадь культурами, чем в оптимальном решении, и получать более высокий доход. В рассматриваемой задаче таким ограничениями являются «урожайность» и «труд механизаторов». Поскольку знак ограничений этих запасов имеют вид ≤, то возникает вопрос, насколько минимально должно упасть использование этих ресурсов, чтобы обеспечить увеличение дохода. Ответ показан в графе Допустимое увеличение. Ресурс «Труд механизаторов» есть смысл увеличить самое большое на 837,5 чел.-дн., а ресурс «урожайность» есть смысл увеличить самое большое на 33500 ц. Ценность дополнительной единицы ресурса ί (теневая цена) рассчитывается только для дефицитных ресурсов (см. отчёт по устойчивости). Анализ использования ресурсов в оптимальном плане выполняется с помощью второй теоремы двойственности: если Yi>0, то 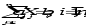 (14) (14)если 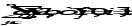 (15) (15)Ресурсы «урожайность» и «труд механизаторов» имеют отличную от нуля оценки 100 и -0,5 – эти ресурсы полностью используется в оптимальном плане и является дефицитными, т.е. сдерживающим рост целевой функции. Правая часть этого ограничения равна левой части: 0,5Х1 + Х2 + 5Хз ≤5000, 0,5×325+ 4837,5 + 0,5×0 = 5000= 5000, 20Х1 ≥6500, 20×325= 6500= 6500, Ресурсы «площадь пашни» и «ручной труд» используется не полностью (5162,5 < 6000) и (2581,25 < 9000) , поэтому имеют нулевую двойственную оценку Υ1= 0 и Υ3= 0). Х1 + Х2 + Хз ≤ 6000, 325+ 4837,5 + 0 = 5162,5 ≤ 6000. 0,5Х1 + 0,5Х2 + 20Хз ≤ 9000, 0,5×325+0,5×4837,5 + 20×0 = 2581,25 ≤ 9000. Эти ресурсы не влияют на распределение культур на пашне. Общая стоимость используемых ресурсов при посевной площади пшеницей 325 га. и посевной площади гречихой 4837,5 га. составит 496750 руб.: 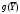 = 6000×Υ1 + 5000×Υ2+ 9000×Υ3 +6500 Υ4 = = 6000×Υ1 + 5000×Υ2+ 9000×Υ3 +6500 Υ4 = = 6000×0+ 5000×100 + 9000×0 + 6500×(-0,5) = 496750 руб. Анализ эффективности отдельных изделий выполняется на основе соотношений из второй теоремы двойственности: если 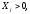 то то 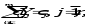 (16) (16)если 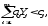 то то 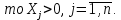 (17) (17)Поясним равенство нулю Х3. Если продукт вошел в оптимальный план (Хj > 0), то в двойственных оценках оно не убыточно, т.е. количество ресурсов, затраченных на разрабатывание культур, равна его доходу. Такие продукты эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче – это пшеница и гречиха. Если стоимость ресурсов, затраченных на выращивание урожая, больше его стоимости, то это продукт не войдет в оптимальный план из-за его дороговизны. В нашей задаче в план выпуска не вошла культура картофель, потому что затраты по ней превышают доход на 200 руб. Разницу между правым и левыми частями ограничений двойственной задачи можно найти в Отчете по устойчивости в столбце Приведенная стоимость. Список литературы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
