1. Предмет и задачи курса эмм, его место в системе экономических дисциплин 3
 Скачать 322.14 Kb. Скачать 322.14 Kb.
|
Задание 4Мясокомбинат имеет в своем составе четыре завода, на каждом из которых может изготовляться три вида колбасных изделий. Мощности каждого из заводов соответственно равны: 320, 280, 270, 350 т/сутки. Ежедневные потребности в колбасных изделиях известны и соответственно равны: 450, 370,400 т. Зная себестоимость одной тонны каждого вида колбасных изделий на каждом заводе которые определяются матрицей: 23 4 1 5 3 6 4 2 7 8 5 Найти такое распределение выпуска колбасных изделий между заводами, при котором себестоимость изготовляемой продукции является минимальной. Решение: Проверим какой является задача, открытой или закрытой. Заявки магазинов 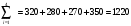 Запасы хозяйств 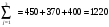 Т.к. 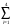 = = 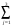 ,то задача является закрытой. ,то задача является закрытой.Запишем экономико-математическую модель задачи. 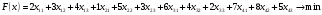 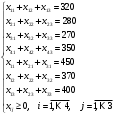 Найдём опорное решение методом северо-западного угла.
Валовый сбор будет равен: 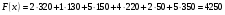 Проверим на оптимальность полученное решение. Вычислим для занятых клеток потенциалы по формуле 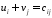 При известных 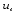 найдём найдём 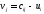 При известных 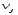 найдём найдём 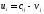 Возьмём 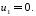 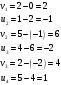 Посчитаем оценки для свободных клеток по формуле 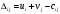 . .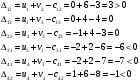 Получили положительную оценку, значит, наш план не является оптимальным. Построим новый цикл для клетки с ненулевой стоимостью с положительной оценкой 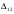 . .
Вычислим для занятых клеток потенциалы. 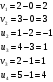 Посчитаем оценки для свободных клеток по формуле 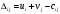 . .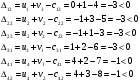 Т.к. все оценки отрицательные, то решение является оптимальным. 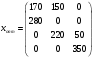 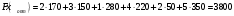 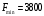 (руб.) – минимальная себестоимость изготовляемой продукции. (руб.) – минимальная себестоимость изготовляемой продукции.. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

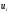

 320 _
320 _ 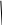 +
+ 130+
130+