Шпоры. 1. Предмет и задачи статистики
 Скачать 0.57 Mb.
|
 В этом случае систему уравнений МНК выглядит следующим образом:  Эта система решается различными способами. Например через парные коэффициенты корреляции и среднеквадратичное отклонения. 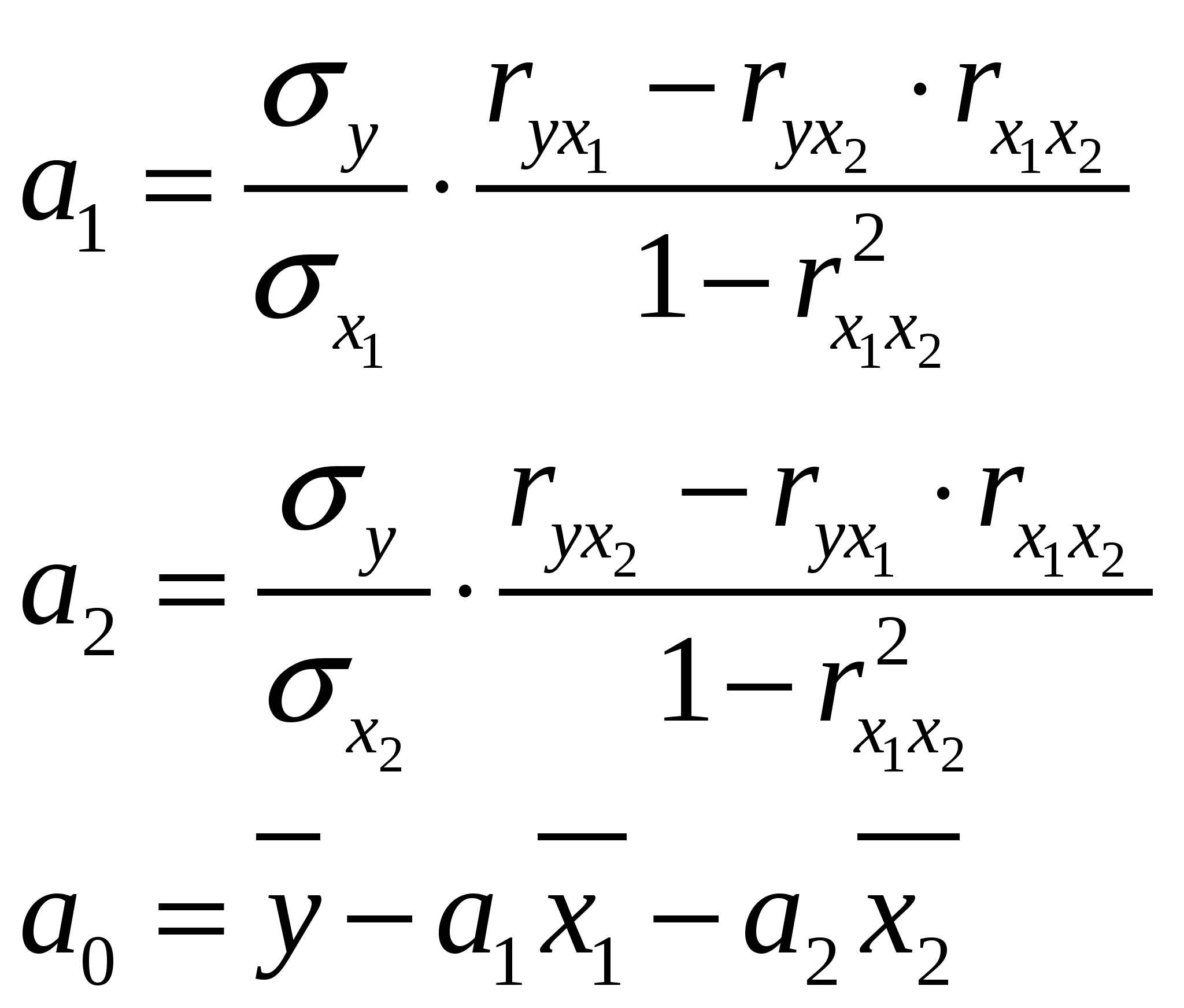 54. Анализ уравнения множественной регрессии. Частные коэффициенты регрессии, эластичности,  - коэффициенты.Частные коэффициенты регрессии сами по себе не позволяют определить какие из факторов оказывают большее влияние на у, поскольку факторы измерены разными единицами, а так же в развитии каких факторов заложены наиболее существенные резервы улучшения значения y. Для ответа на эти вопросы вычисляются частные коэффициенты эластичности и β – коэффициенты. Различия в единицах измерения факторов устраняются с помощью частных коэффициентов эластичности, которые рассчитываются по формуле:  , где ai – частный коэффициент при регрессии при i факторе; xi – среднее значение факторного признака; y – среднее значение результативного признака.Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется результативный признак у при изменении i фактора на 1%. И при фиксированном положении на среднем уровне остальных факторов. Для определения факторов в развитии который заложены наибольшие резервы улучшения результативного признака у необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это делается с помощью частных β – коэффициентов, которые вычисляется по формуле:  Частный β коэффициент показывает на какую часть своего среднеквадратического отклонения σу изменится результативный признак у при изменении i факторного признака (xi) на величину его среднеквадратического отклонения σх. 55. Оценка тесноты связи между признаками: парные и частные коэффициенты корреляции. В рамках многофакторного корреляционного анализа также находится разного рода характеристики тесноты связи между результативными признаками и влияющими на него факторными. Это частные и парные коэффициенты корреляции, а также коэффициенты множественной корреляции и детерминации. Для оценки тесноты связи между 2-мя из рассматриваемых переменных без учета их взаимодействия с другими переменными применяют парные коэффициенты корреляции. Методика расчета и интерпретация парных коэффициентов в корреляции аналогична линейному коэффициенту корреляции:  ;  .Частные коэффициенты корреляции показывают тесноту связи результативного признака у с рассматриваемым факторным признаком в условиях исключительного влияния других включенных в модель факторов. При этом влияние факторов, не включенных в модель, остается не исключенным. Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции. Например, в случае зависимости у от 2-х факторов необходимо рассчитывать 2 частных коэффициента корреляции:  ,  . - частный коэффициент корреляции между результативным признаком у и фактором х1 при исключающем влиянии фактора х2. Показывает, какую долю составляет вариация у, вызванная фактором х1 в вариации у под действием всех факторов, кроме фактора х2. Парные и частные коэффициенты корреляции могут принимать значения от -1 до +1. 56. Оценка тесноты связи между признаками: коэффициенты множественной корреляции и детерминации. Для оценки тесноты связи между результативным признаком у и всей совокупностью, включенных в модель факторов хi рассчитывают коэффициент множественной корреляции. Он служит основным показателем линейной корреляционной связи. Например, в случае линейной 2-х факторной регрессии коэффициент множественной корреляции R рассчитывается по формуле:  .Величину R2 называют коэффициентом множественной детерминации. Он показывает, какая доля вариации результативного признака у объясняется влиянием факторов, включенных в уравнение множественной регрессии. R2 может принимать значения от 0 до +1. 57. Коэффициенты корреляции рангов (ККР). ККР Спирмэна. Применение линейного коэффициента корреляции (r) является обоснованным лишь в условиях нормального, или близкого к нормальному, распределения изучаемых признаков. Для измерения интенсивности корреляционной связи между количественными признаками, форма распределения которых отличается от нормальной, а также между атрибутивными признаками, значения которых допускают ранжирование, используют коэффициенты корреляции рангов. Они основаны на измерении корреляции не самих значений признака, а их рангов, т.е. порядковых номеров в ранжированном ряду значений. Коэффициенты корреляции, базирующиеся на использовании рангов, были предложены англичанами Спирмэном и Кендэлом. Для расчета ККР Спирмэна значения признаков x и y нумеруют в порядке возрастания от 1 до n. Порядковые номера используются в качестве рангов: Nx и Ny.. Если встречаются несколько одинаковых значений х и у, то каждому из них присваивается ранг, равный частному от деления суммы рангов, приходящейся на эти одинаковые значения, на число одинаковых значений; затем ранги отдельных значений фактического признака х сопоставляют с рангами результативного признака у, рассчитывают разности di:  .Степень тесноты связи между признаками определяется по формуле:  , n – число сопоставимых пар.58. Коэффициенты корреляции рангов (ККР). ККР Кендэла. Применение линейного коэффициента корреляции (r) является обоснованным лишь в условиях нормального, или близкого к нормальному, распределения изучаемых признаков. Для измерения интенсивности корреляционной связи между количественными признаками, форма распределения которых отличается от нормальной, а также между атрибутивными признаками, значения которых допускают ранжирование, используют коэффициенты корреляции рангов. Они основаны на измерении корреляции не самих значений признака, а их рангов, т.е. порядковых номеров в ранжированном ряду значений. Коэффициенты корреляции, базирующиеся на использовании рангов, были предложены англичанами Спирмэном и Кендэлом. Кендэл предложил другую меру связи между признаками х и у:  .Для определения  ранги значения величин фактического признака х располагают в порядке их возрастания. В таком же порядке располагают ранги соответствующих значений у.Для определения P устанавливают, сколько чисел находится справа от каждого из этих элементов последовательности рангов признака у, превышающих ранг рассматриваемого элемента. Суммируют соответствующие (n-1) величин, получают значения P. Для определения Q подсчитывают, сколько чисел находится справа от каждого из элементов последовательности рангов признака у, меньше этого ранга. Эти величины берут со знаком «-» и в сумме дают значение Q.  .59.Измерение частоты связи между атрибутивными признаками: коэффициент ассоциации. Для измерения тесноты связи 2-х атрибутивных признаков, имеющих только 2 варианта значений, используют более простой показатель: коэффициент ассоциации. При этом исходные данные сводят в 4-х клеточную комбинационную таблицу:
a,b,c,d – частоты сопоставимых признаков (частота совместимости появления):  ,  . . Сильная связь между атрибутивными признаками.60. Измерение частоты связи между атрибутивными признаками: коэффициент взаимной сопряженности. Измерение тесноты связи между атрибутивными признаками. Тесноту связи между атрибутивными признаками измеряют с помощью специальных показателей. Это измерение основывается на подсчете частоты совместимости появления атрибутивных признаков. Чем выше относительная частота такой совместимости появления, тем сильнее связь между рассматриваемыми признаками. Наиболее общим показателем является коэффициент взаимной сопряженности А.А. Чупрова. Он применяется для измерения тесноты связи между 2-мя атрибутивными признаками, имеющими больше 2 вариантов значений. Коэффициент Чупрова рассчитывается по формуле:  ,К1, К2 – число возможного значения 1 и 2-го атрибутивного признака.  - показатель взаимной сопряженности. |