Шпоры. 1. Предмет и задачи статистики

• Название: 1. Предмет и задачи статистики
• Анкор: Шпоры.doc
• Дата: 20.09.2018
• Размер: 0.57 Mb.
• Имя файла: Шпоры.doc
• Тип: Документы; #24873
• Категория: Математика
• страница: 3 из 5

Показатель эксцесса является характеристикой островершинности распределения. Коэффициент эксцесса рассчитывается по формуле, для нормального распределения Е_х=0, т.е. . Для более островершинных распределений, чем нормальное Е_х>0. Для более плосковершинных Е_х<0.
26. Статистические группировки. Типологическая группировка.

Группировкой в статистике называют разделение единиц сов-ти на группы по существенным варьирующим признакам. Признаки, положенные в основание группировки, называются группировочными. Они делятся на атрибутивные (качественные) и количественные. Группировать единицы сов-ти можно по одному признаку (простая группировка), а можно группы, образованные по одному признаку, разбить на подгруппы по другому признаку. Группировки, где применяются 2 и более признака, взятые в комбинации, называются комбинированные.

Статистическая группировка может преследовать различные цели, основными из них являются:

1. Выделение качественно-однородных сов-ей (такие группировки называются типологическими).

2. Изучение состава сов-ти по тем или иным признакам (структурныегруппировки)

3. Изучение причинно-следственных связей между признаками в пределах той или иной сов-ти (аналитическиегруппировки).

К типологическим относят все группировки, которые характеризуют качественные особенности и различия между типами явлений (пример: данные о социальном составе населения).
27. Статистические группировки. Структурная группировка.

Группировкой в статистике называют разделение единиц сов-ти на группы по существенным варьирующим признакам. Признаки, положенные в основание группировки, называются группировочными. Они делятся на атрибутивные (качественные) и количественные. Группировать единицы сов-ти можно по одному признаку (простая группировка), а можно группы, образованные по одному признаку, разбить на подгруппы по другому признаку. Группировки, где применяются 2 и более признака, взятые в комбинации, называются комбинированные.

Статистическая группировка может преследовать различные цели, основными из них являются:

1. Выделение качественно-однородных сов-ей (такие группировки называются типологическими).

2. Изучение состава сов-ти по тем или иным признакам (структурныегруппировки)

3. Изучение причинно-следственных связей между признаками в пределах той или иной сов-ти (аналитическиегруппировки).

Структурные группировки позволяют выявить внутреннее строение явлений. Они дают информацию о том, из каких частей состоит изучаемая сов-ть и какими показателями характеризуются ее отдельные части. Если типологические группировки имеют главным образом познавательное значение, то структурные - служат для получения выводов о текущем положении дел, используются для оперативного руководства работы предприятия, служат базой для выявления имеющихся резервов.
28. Статистические группировки. Аналитическая группировка.

Группировкой в статистике называют разделение единиц сов-ти на группы по существенным варьирующим признакам. Признаки, положенные в основание группировки, называются группировочными. Они делятся на атрибутивные (качественные) и количественные. Группировать единицы сов-ти можно по одному признаку (простая группировка), а можно группы, образованные по одному признаку, разбить на подгруппы по другому признаку. Группировки, где применяются 2 и более признака, взятые в комбинации, называются комбинированные.

Статистическая группировка может преследовать различные цели, основными из них являются:

1. Выделение качественно - однородных сов-ей (такие группировки называются типологическими).

2. Изучение состава сов-ти по тем или иным признакам (структурныегруппировки)

3. Изучение причинно-следственных связей между признаками в пределах той или иной сов-ти (аналитическиегруппировки).

Аналитические группировки позволяют исследовать причинно-следственные связи между признаками однородных явлений и выявлять факторы развития сов-ти. Взаимосвязанные признаки делят на факторные и результативные.

Факторным называется признак, под воздействием которого изменяется другой, зависящий от него признак, называемый результативным. Чтобы исследовать взаимосвязь между отобранными признаками с помощью аналитической группировки, необходимо произвести группировку единиц сов-ти по факторному признаку и по каждой группе исчислить средние значения результативного признака, вариация которого от группы к группе будет указывать на наличие или отсутствие взаимосвязи.
29.Ряды динамики. Виды рядов динамики.

Ряд динамики - это последовательность числовых значений изучаемого показателя, расположенных в хронологическом порядке. Числовые значения показателя, составляющие динамический ряд, называется уровнями ряда. Уровни динамического ряда могут относиться к отдельным моментам или интервалу времени. В зависимости от этого различают моментные и интервальные ряды динамики.

Моментным называется ряд, уровни которого характеризуют величину изучаемого показателя по состоянию на определенные моменты времени.

Интервальным называется ряд, уровни которого характеризуют величину показателя за определенные периоды времени.

Кроме того, ряды динамики подразделяют на ряды абсолютных, относительных и средних величин. Ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин - как производные от них. При изучении динамики социально-экономических явлений чаще используют производные интервальные ряды.
30. Правило построения рядов динамики.

Необходимым условием объединения уровней в единый динамический ряд является сопоставимость этих уровней.

Несопоставимость уровней может быть вызвана:

1. Изменением административных территориальных границ;

2. Изменением даты учета показателей;

3. Изменением единиц измерения показателей;

4. Изменением масштаба цен;

5. Различной продолжительностью периодов времени, к которым относятся отдельные уровни;

6. Изменением методологии расчета показателей;

7. Изменения в составе объектов, охваченных наблюдением.

Основное правило построения рядов динамики заключается в том, что уровни ряда нужно проверять на сопоставимость, несопоставимые уровни следует приводить к сопоставимому виду с помощью дополнительных расчетов и если это невозможно, то исключать.
31. Показатели изменения уровней динамического ряда.

При изучении рядов динамики определяют направление и скорость изменения его уровней. С этой целью рассчитывают такие показатели, как абсолютные приросты, темпы роста и прироста. Для иллюстрации расчета показателей будем рассматривать динамический ряд из n-уровней: у₁,у₂,…,у_n.

Темпы роста показывают во сколько раз некоторый уровень больше или меньше другого уровня ряда, т.е. характеризует интенсивность изменения уровней ряда. Если каждый уровень сопоставляется с предыдущим уровнем ряда, то получают цепные темпы роста ,t=2;…;n. Если все уровни ряда сопоставимы с одним и тем же уровнем, принятым за базу сравнения, то получают базисные темпы роста.

Между цепными и базисными темпами роста существует взаимосвязь, позволяющая в случае необходимости переходить от одного к другим. Например, произведение цепных темпов роста дает базисные темпы роста. Результат деления двух базисных темпов роста равен цепному темпу.

Абсолютный прирост характеризует абсолютную скорость изменения уровней ряда. Он показывает, на сколько единиц измерения некоторый уровень больше или меньше другого уровня ряда. Абсолютные приросты могут рассчитываться как цепные или как базисные .

Темп прироста показывает на сколько % некоторый уровень больше или меньше другого уровня ряда, он характеризует абсолютное изменение темпа роста и рассчитывается по формуле,,.

Разделив абсолютный прирост на темп прироста за соответствующий период, получим показатель абсолютного значения 1% прироста. Абсолютное значение 1% прироста = 0,01 предыдущего уровня ряда. Для базисных абсолютных приростов и темпов прироста расчет этого показателя не имеет смысла, т.к. будет получаться одно и то же число.
32. Обобщающие показатели уровней ряда.

1. Средняя хронологическая - средняя, исчисленная из показателей, изменяющихся во времени. Она представляет собой среднее значение показателя в течение изучаемого периода времени. Для интервального ряда с разными интервалами средн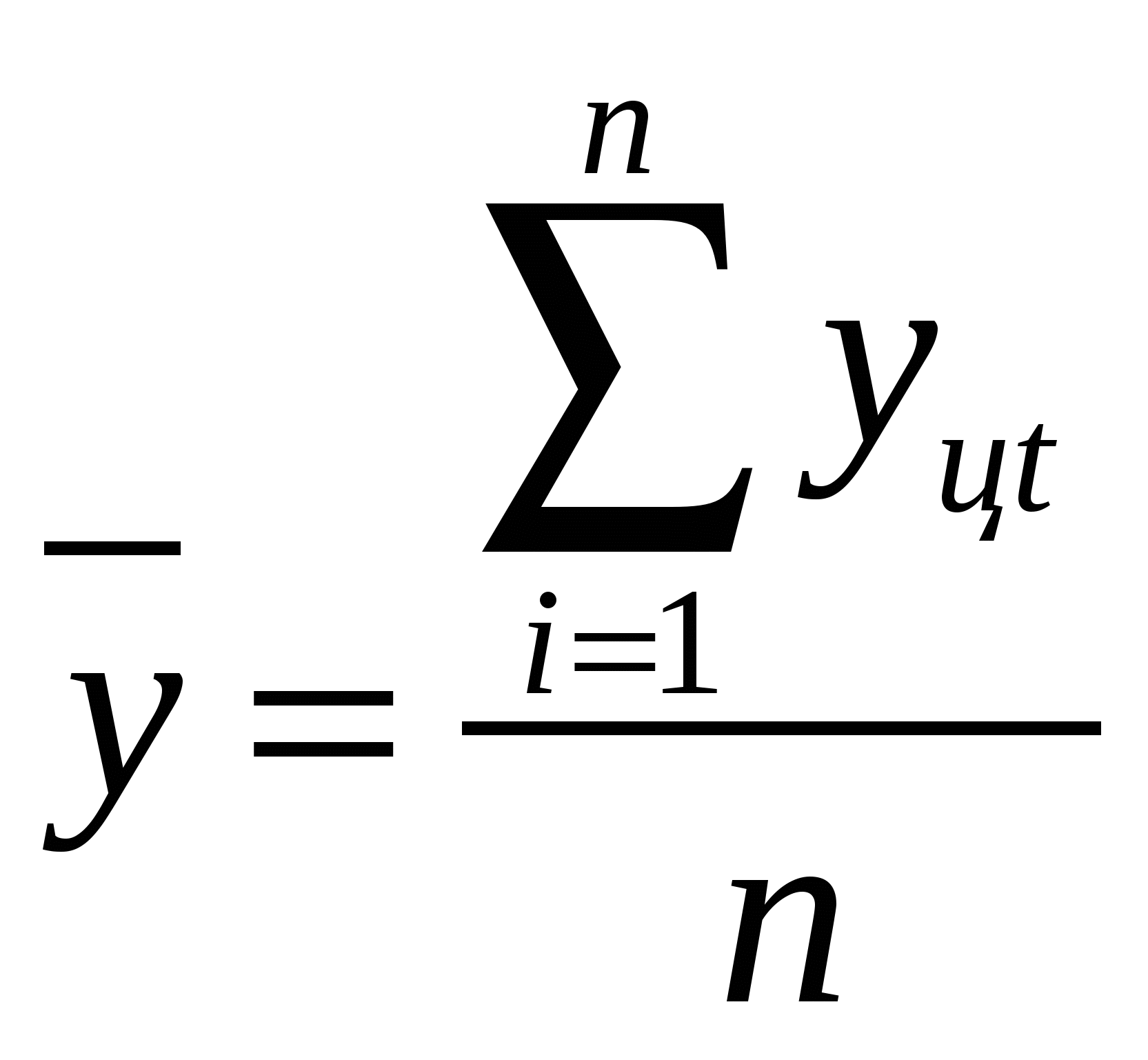яя хронологическая рассчитывается по формуле. Для моментного ряда с равноотстоящими уровнями средняя хронологическая рассчитывается по формуле.

2. Конкретные уровни ряда отличаются от своей средней хронологической. Величину этого отклонения можно оценить с помощью среднего квадратического отклонения .

3. Коэффициент вариации . Коэффициент вариации является относительной величиной и может использоваться для сравнения колеблемости различных рядов динамики.

4. Средний абсолютный прирост характеризует среднюю скорость изменения показателя в течении изучаемого периода времени .

5. Средние темпы роста показывают среднюю интенсивность изменения показателя за рассматриваемый период. Рассчитывается по формуле среднегеометрической .

Средний темп прироста рассчитывается на основе среднего темпа роста по формуле .
33. Выравнивание рядов динамики.

Изучая динамическую часть, стремятся выявить общую тенденцию в изменении его уровней, освобожденную от действия случайных факторов. Одним из способов обработки динамических рядов с целью выявления тенденции развития (тренд) является аналитическое выравнивание. При использовании этого способа каждый фактический уровень ряда y_t рассматривается как: , где y_t - неслучайная составляющая, отражающая тренд и описываемая определенным аналитическим уравнением, -случайная составляющая, характеризующая отклонение от тренда.

Задача аналитического выравнивания состоит в определении на основе фактических данных вида функции f(t)= , отыскании ее по параметров и расчете теоретических значений у по найденной формуле.
34. Метод наименьших квадратов.

При использовании МНК значения постоянных параметров уравнения тренда определяют таким образом, чтобы сумма квадратов отклонения фактических уравнений ряда от теоретических уровней была минимальной. .

Чтобы получить параметры, удовлетворяющие этому условию, нужно приравнять к нулю первую производную критерия z по каждому из из искомых параметров dz/da_i=0, где i=0,1.. В результате будет получена система из k+1 нормальных уравнений с таким же числом неизвестных. Решение этой системы относительно величин a_i и дает искомые оценки постоянных параметров уравнения тренда. Чем длиннее динамический ряд, тем более надежными являются результаты, полученные с помощью МНК. При этом все уровни ряда считаются равноценными, т.е. более ранние и более поздние наблюдения учитываются с одинаковым весом. Достоинством МНК является относительная простота реализации.
35. Свойства оценок параметров функций, полученных МНК.

Фактические уровни ряда не совпадают с теоретическими уровнями, полученные с помощью уравнения тренда, т.е. можно записать, величину назовем возмущением. Относительно возмущений сделаем следующие допущения:

1. Возмущения являются случайной переменной;

2. Математическое ожидание ;

3. Дисперсия возмущения постоянна D()=const;

4. Последовательное значение не зависят друг от друга.

Если сделанные допущения верны, то получаемые с помощью МНК оценки параметров обладают рядом свойств, а именно:

1. Оценки являются несмещенными. Свойство несмещенности означает, что получаемые в МНК оценки параметров концентрируются вокруг неизвестных истинных значений параметров.

2. Оценки являются состоятельными. Свойства состоятельности означает, что при увеличении объема наблюдений оценки параметров МНК все плотнее концентрируются вокруг неизвестных истинных значений параметров.

3. Оценки являются эффективными, т.е. они имеют минимальную дисперсию по сравнению с оценками параметров, полученных любыми другими методами. Свойство эффективности является наиболее важным, поскольку именно оно определяет степень возможной ошибки при использовании уравнения тренда.

Если допущения 3 или 4 не выполняются, то свойства несмещенности и состоятельности оценок сохраняются, однако оценки оказываются менее эффективные, чем в случае, когда эти допущения выполняются.
36. Выравнивание ряда по полиному 1 степени с помощью МНК.

Обычный метод МНК применим только к линейным, относительно своих постоянных параметров, функциям. Например, к полиномам любой степени:

- полином 1 степени;

- полином 2 степени;

- полином 3 степени.

Критерий МНК в этом случае выглядит следующим образом (в случае полинома 1 степени): .

Системы нормальных уравнений МНК для этих функций, для полиномов выглядят следующим образом:

- для полинома 1 степени.
37. Выравнивание ряда по полиному 2 степени с помощью МНК.

- для полинома 2 степени
38. Выравнивание ряда по полиному 3 степени с помощью МНК.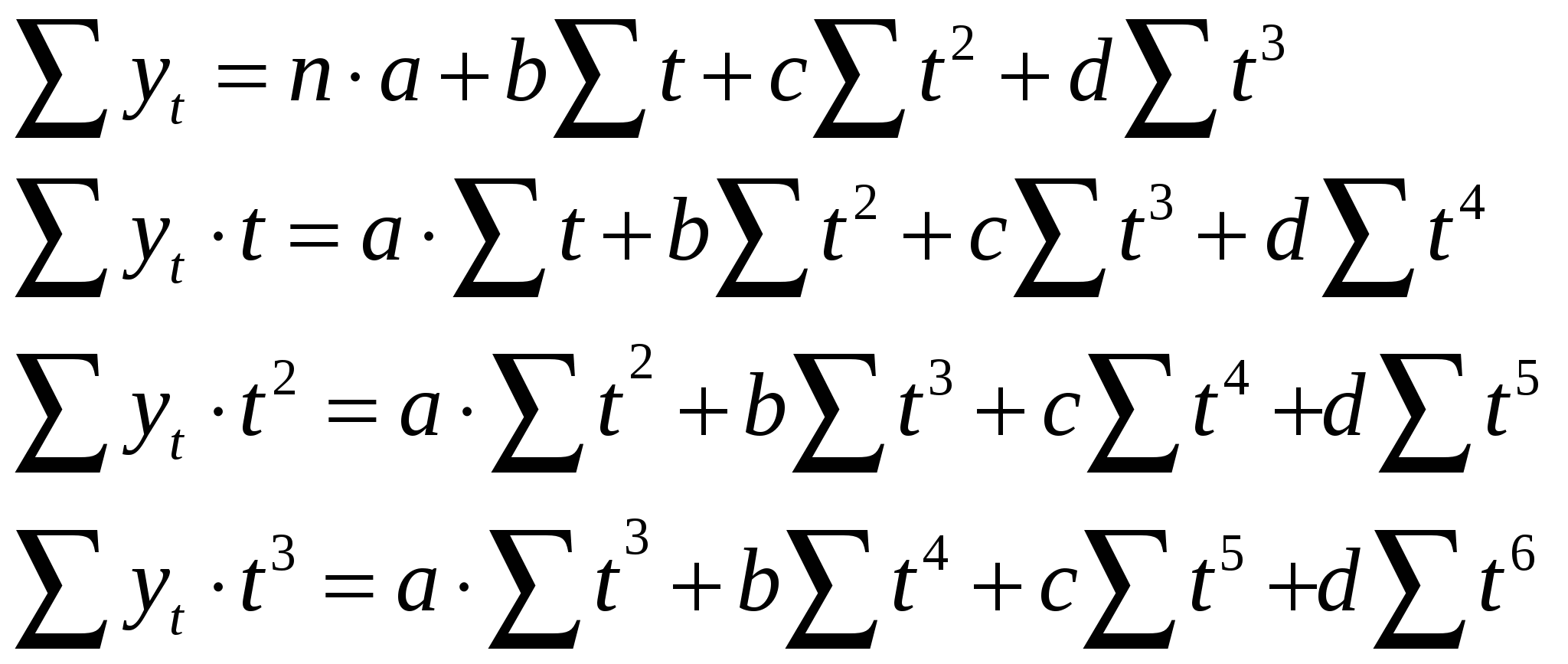

- для полинома 3 степени.

39. Расчет параметров полиномов с помощью МНК при переносе начала координат.

Совместное решение систем уравнений позволяет вывести формулы для оценки параметров полиномов. Для полинома первой степени получаем.t – номер момента времени. .

Для упрощения расчетов можно использовать один из способов:

Способ переноса начала координат в середину ряда. В том случае упрощаются сами системы уравнений, уменьшаются абсолютные значения величин, участвующих в расчете. Процедура переноса начала координат различается для рядов с четным и нечетным числом уровней.

Более простая ситуация, когда в ряду нечетное число уровней:

-(n-1)/2…-3 -2 -1 0 1 2 3…(n-1)/2.

Более сложная ситуация, когда в ряду четное число уровней – центр ряда между двумя центральными уровнями:

-(n-1) -5 -3 -1 1 3 5 (n-1)

После переноса начала координат все суммы t=0,кроме степени