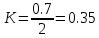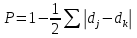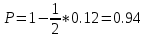Анализ неравномерности распределения

• Название: Анализ неравномерности распределения
• Дата: 05.11.2020
• Размер: 30.8 Kb.
• Имя файла: lektsia_po_kontsentratsii.docx
• Тип: Документы; #148133

1. АНАЛИЗ НЕРАВНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ

Необходимо более детально (глубоко) проанализировать ряды распределения:

• 
  с помощью оценки неравномерности распределения единиц совокупности по значению группировочного признака;
  
• 
  путем исследования степени концентрации.
  

Для этого соответственно рассчитывают показатели дифференциации и концентрации. Перейдем к исследованию степени концентрации.

Вместе с распределением единиц совокупности по какому-либо признаку целесообразно изучение распределения по этим же группам другого показателя (таблица 1.2). Второе распределение может быть как равномерным (соответствовать распределению количества единиц совокупности), так и неравномерным.

Данное направление анализа актуально для характеристики равномерности распределения материальных и финансовых ресурсов по регионам; числа занятых – по отраслям; доходов и имущества – по отдельным группам населения.

Неравномерность распределения оценивают прежде всего с помощью коэффициентов концентрации и локализации.

Оценка концентрации основывается на отклонениях частостей двух распределений: первое распределение – это распределение по числу единиц совокупности ; второе – распределение по величине признака.

Если распределение по величине признака в совокупности равномерное, то частости = ; отклонения частостей свидетельствуют об определенной концентрации. Верхняя граница суммы отклонений , а поэтому коэффициент концентрации определяется как полусумма модулей отклонений:

Границы колебаний: :

• 
  при = 0, констатируем равномерное распределение;
  
• 
  при = 1, фиксируем полную концентрацию;
  
• 
  чем большая степень концентрации, тем больше значение.
  

Представленные в таблице 1.2 данные о распределении предприятий региона по формам собственности и по количеству занятого населения свидетельствуют о неравномерности распределения. На основании формулы произведем расчет коэффициента концентрации

Таблица 1.2

К расчету коэффициентов концентрации и локализации

Форма собственности	В % к итогу		Модуль отклонения частостей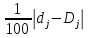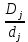
	число предприятий	численность занятого населения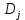
Государственная	4,4	39,4	0,350	8,955
Коллективная	57,5	31,4	0,261	0,546
Частная	29,6	29,1	0,005	0,983
Другие	8,5	0,1	0,084	0,012
Итого	100,0	100,0	0,700	-

Величина данного показателя свидетельствует о среднем уровне концентрации занятых на предприятиях различных форм собственности (или о средней степени неравномерности распределения).

Таким образом, коэффициент концентрации является обобщающей характеристикой отклонения распределения от равномерного.

Для каждой j-й группы совокупности рассчитывают коэффициент локализации. Коэффициент локализации характеризует соотношение частостей двух распределений и часто используется для оценки территориального распределения:





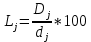
При равномерном распределении все значения Lj=1. В случае концентрации значений признака в j-й группе Lj > 1и наоборот.

Рассчитанные по данным таблицы 7.2 коэффициенты локализации свидетельствуют о концентрации занятого населения на предприятиях государственной формы собственности.

Для обеспечения сопоставимости структур одного объекта в динамике используют вторичные группировки. Для анализа изменений, например, в распределении населения по доходам (расходам), совокупность разбивают на равные по численности населения группы: на 10 групп по 10 % единиц в каждой или на 5 групп по 20 % единиц в каждой.

По такому принципу строят кривую концентрации Лоренца и на ее основе рассчитывают коэффициент концентрации доходов Джини, в котором

• 
  доля населения j-й социальной группы в общей численности населения, – доля доходов j-й социальной группы населения в общем объеме доходов.
  

Кривая концентрации Лоренца дает наглядное представление о

характере распределения. Ее строят в прямоугольной системе координат, где на оси абсцисс и ординат наносят одинаковые масштабы шкал от 0 до 100. На оси ОХ откладывают значения кумулятивных долей (частостей), которые характеризуют распределение населения, а на оси ОУ – кумулятивные частости доходов.

В случае равномерного распределения доходов кумулятивные частости населения и доходов совпадают. Линией равномерного распределения является диагональ квадрата. Она означает полное отсутствие концентрации. Какие-либо отклонения от диагонали свидетельствуют о неравномерности распределения. Чем больше кривая Лоренца будет отклоняться от диагонали квадрата, тем более неравномерное распределение и выше концентрация доходов в отдельных группах населения. При полностью неравномерном распределении точкам 0, 20, 40, 60, 80, 100 по оси ОХ будут соответствовать 0,

0, 0, 0, 0, 100 по оси ОУ. В таком случае получаем линию полного неравномерного распределения.

На основе сравнения площадей фигур, первая из которых ограничена диагональю и кривой Лоренца, а другая – диагональю и линией полного неравномерного распределения, рассчитывают коэффициент концентрации доходов Джини (G). На практике для его определения используют следующую

приближенную формулу:



.

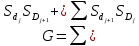
Коэффициент Джини принимает значения от 0 до 1; чем ближе к 1, тем больше степень концентрации и неравномерности распределения доходов между группами населения.

В таблице 1.3 приведены данные о распределении доходов населения между 20 %-ми группами.

Таблица 1.3

Распределение денежных доходов населения региона по 20%-м группам

20%-ые группы населения	Доля группы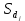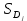
	в общей численности населения	в общих денежных доходах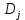
Первая (с наименьшими доходами)	0,2	0,080	0,2		0,080
Вторая	0,2	0,133	0,4		0,213
Третья	0,2	0,181	0,6		0,394
Четвертая	0,2	0,245	0,8		0,639
Пятая (с наибольшими доходами)	0,2	0,361	1,0		1,000
Итого	1,0	1,000	х		х

На рисунке представлена кривая концентрации Лоренца, построенная по данным таблицы 7.3.

100


Кумулятивные частости

доходов населения, %
80

60

40
20
0

0 20 40 60 80 100

Кумулятивные частости

численности населения, %

Произведем расчет коэффициента Джини по формуле:

G=(0.2*0.213+0.4*0.394+0.6*0.639+0.8*1)-(0.4*0.08+0.6*0.213+0.8*394+1*0.639)=0.27

Полученный результат свидетельствует о невысокой степени концентрации доходов в отдельных группах населения.

2. ОЦЕНКА ПОДОБИЯ СТРУКТУР РАЗНЫХ СОВОКУПНОСТЕЙ

Аналогично с коэффициентом концентрации рассчитывают коэффициент подобия структур двух совокупностей (P):

Если структуры одинаковые, то P=1 ; если абсолютно противоположные, P=0. Чем более схожие структуры, тем ближе значение Р к 1.

В таблице 1.4 представлена структура потребительских расходов домохозяйств городской и сельской местности региона.

Рассчитаем коэффициент подобия структур:

Так как значение коэффициента близко к 1, то можно констатировать, что в целом структура потребительских расходов домохозяйств почти одинакова.

Таблица 1.4

Структура расходов домохозяйств региона

Потребительские расходы	Структура расходов в домохозяйствах местности, %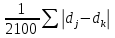
	городской	сельской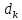
Продовольственные товары	68	67	0,01
Непродовольствен- ные товары	15	21	0,06
Оплата услуг	17	12	0,05
Итого	100	100	0,12
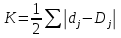