Шпоры. 1. Предмет и задачи статистики

• Название: 1. Предмет и задачи статистики
• Анкор: Шпоры.doc
• Дата: 20.09.2018
• Размер: 0.57 Mb.
• Имя файла: Шпоры.doc
• Тип: Документы; #24873
• Категория: Математика
• страница: 2 из 5

х₀ – нижняя граница модального интервала;

- величина модального интервала;

f₁, f₂, f₃ – частота интервала, предшествующего модальному, модального, следующего за модальным.
13. Обобщенные характеристики вариационного ряда. Медиана.

Кроме средних в качестве обобщенных характеристик признака используют значения конкретных вариантов, занимающих в ранжированном ряду значений признака определенное место.

Наиболее часто используют 2 таких варианта – моду и медиану.

Медианой называют вариант, стоящий в центре ранжированного вариационного ряда.

В дискретном ряду с нечетным числом значений медианой является вариант с порядковым номером (n+1)/2.

Если же вариантов четное число, то медиану определяют как среднюю из 2-х центральных уровней с порядковыми номерами n/2 иn/2+1.

Пример для четного числа: .

При нахождении медианы в интервальном ряду сначала определяется интервал для которого накопленная частота равна или превышает половину суммы частот: (Σf)/2

Внутри этого интервала медиана определяется по формуле:

х₀ – левая граница медианного интервала; - величина медианного интервала; - накопленная частота для интервала, предшествующего медианному; - частота медианного интервала.
14. Показатели вариаций: размах вариаций, среднее линейное отклонение.

Одним из важных элементов анализа вариационных рядов является измерение вариации признака.

Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения могут отличаться от нее мало, а в другом случае эти отличия могут быть велики.

В первом случае вариация признака может быть мала, а во втором велика.

Простейшим показателем вариаций является размах вариаций: .

Размах вариаций дает лишь самое общее представление о размерах вариации, т.к. показывает, как отличаются друг от друга лишь крайние значения признака, но не указывает, на сколько велики отклонения отдельных вариантов друг от друга внутри этого промежутка.

Характеристика вариации будет более точной, если показатель станет учитывать отклонение каждого из вариантов от их средней.

Дело осложняется тем, что сумма всех отклонений отдельных вариантов x от их средней = 0: .

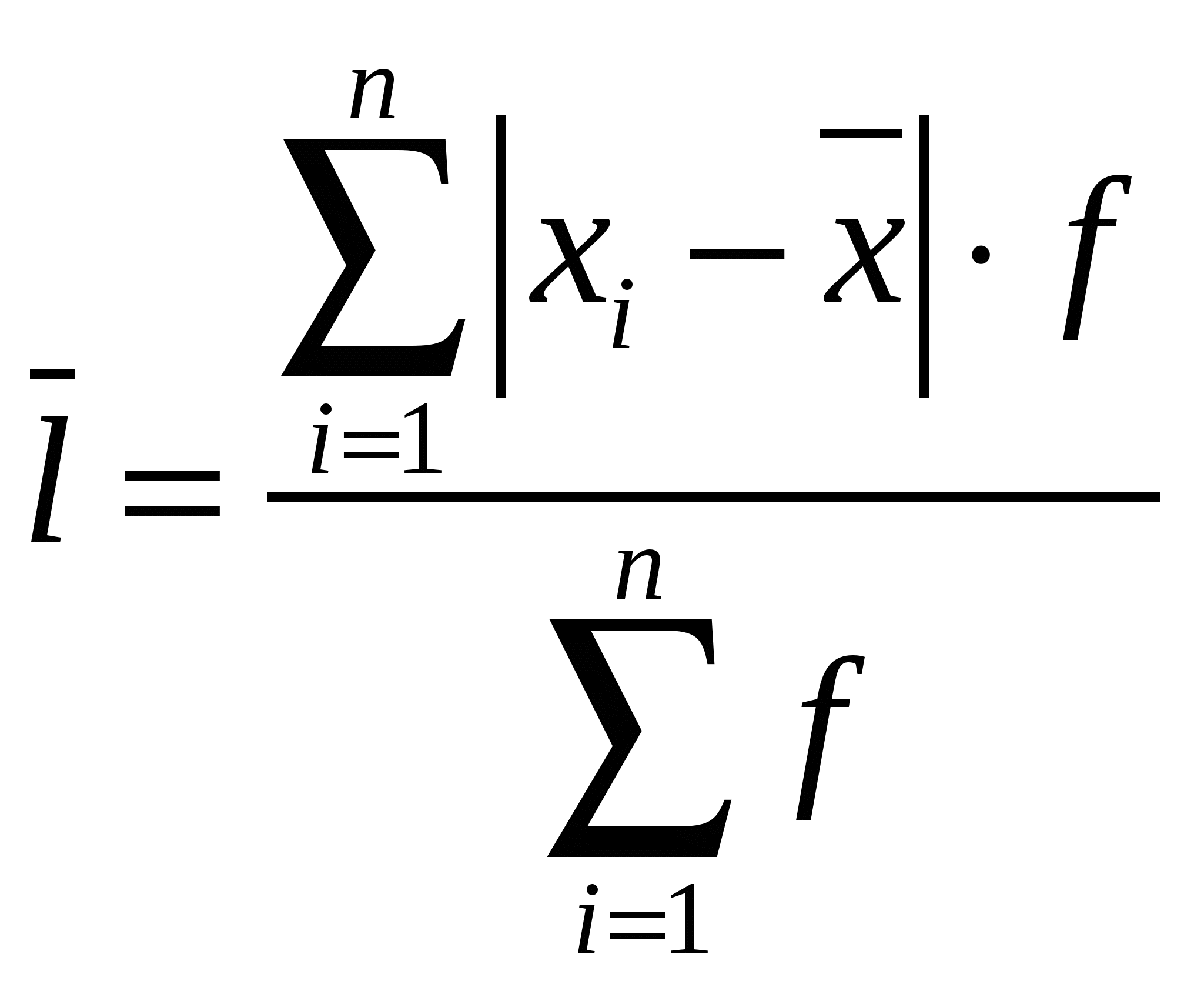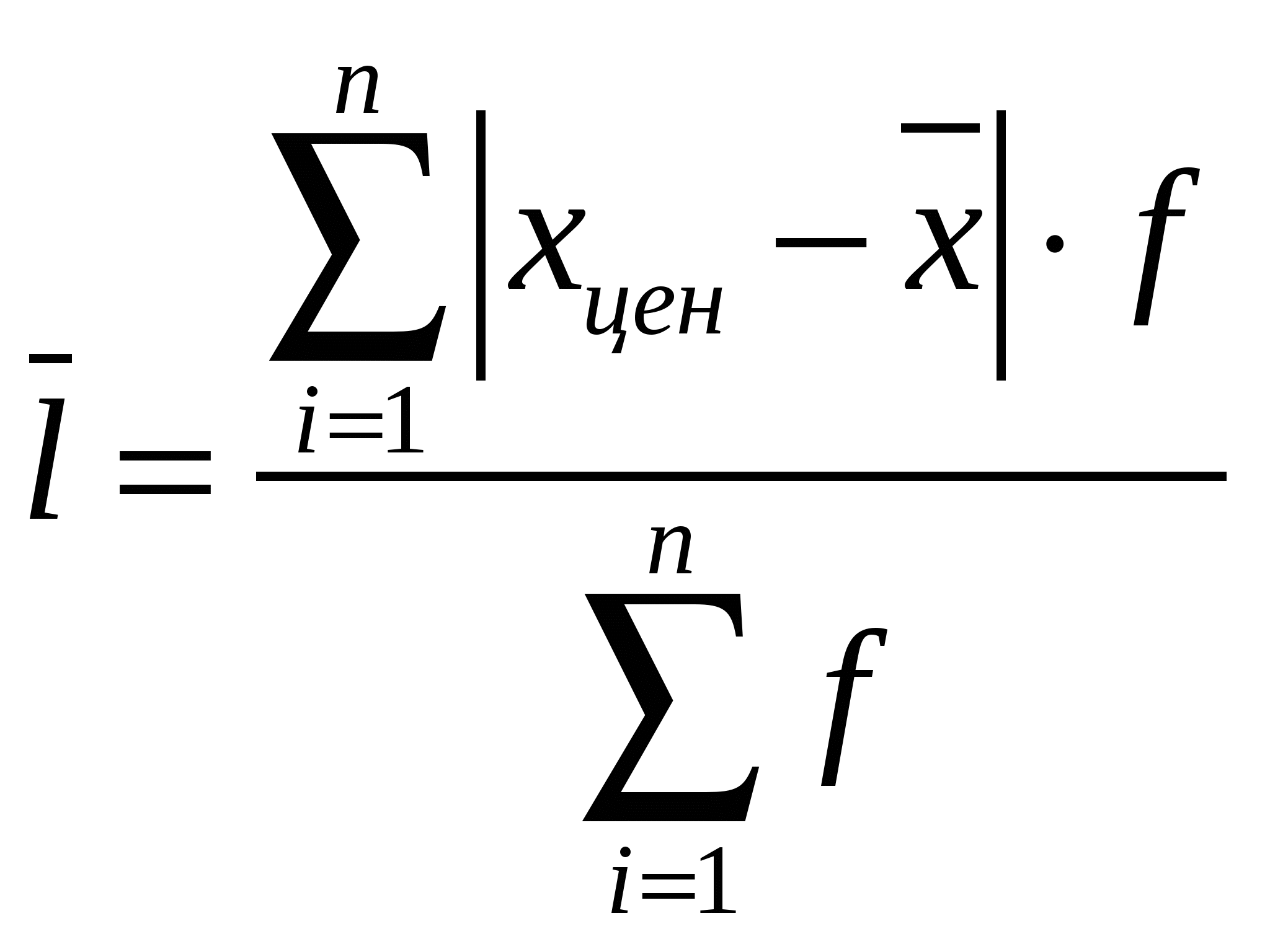В связи с этим находят среднюю либо из модуля отклонений, получая при этом среднее линейное отклонение: (для дискретных рядов); (для интервальных рядов).
15. Показатели вариаций: дисперсия.

Можно рассчитывать среднюю либо из модулей, либо из квадратов отклонений, получая при этом дисперсию: (для дискретных рядов); (для интервальных рядов).

Самый популярный показатель вариации – дисперсия.

Корень квадратный из дисперсии – среднее квадратическое отклонение: .

Дисперсию можно вычислить и по другой формуле: .

Разность среднего квадрата вариантов x и квадрата среднего варианта х – дисперсия.
16. Свойства дисперсии.

1. Дисперсия постоянной величины = 0: ;

2. Дисперсия не изменится, если все варианты увеличить или уменьшить на одно и то же число:;

3. Постоянный множитель выносится за знак дисперсий, возведенный в квадрат: ;

4. Свойство минимальности дисперсии от средней. Дисперсия от средней меньше дисперсии от производного числа x₀ на величину:
17. Правило сложения дисперсий.

Различают следующие виды дисперсий:

Общая дисперсия измеряет вариацию признака x под влиянием всех вызвавших ее факторов. Она измеряется по ранее рассматриваемой формуле: .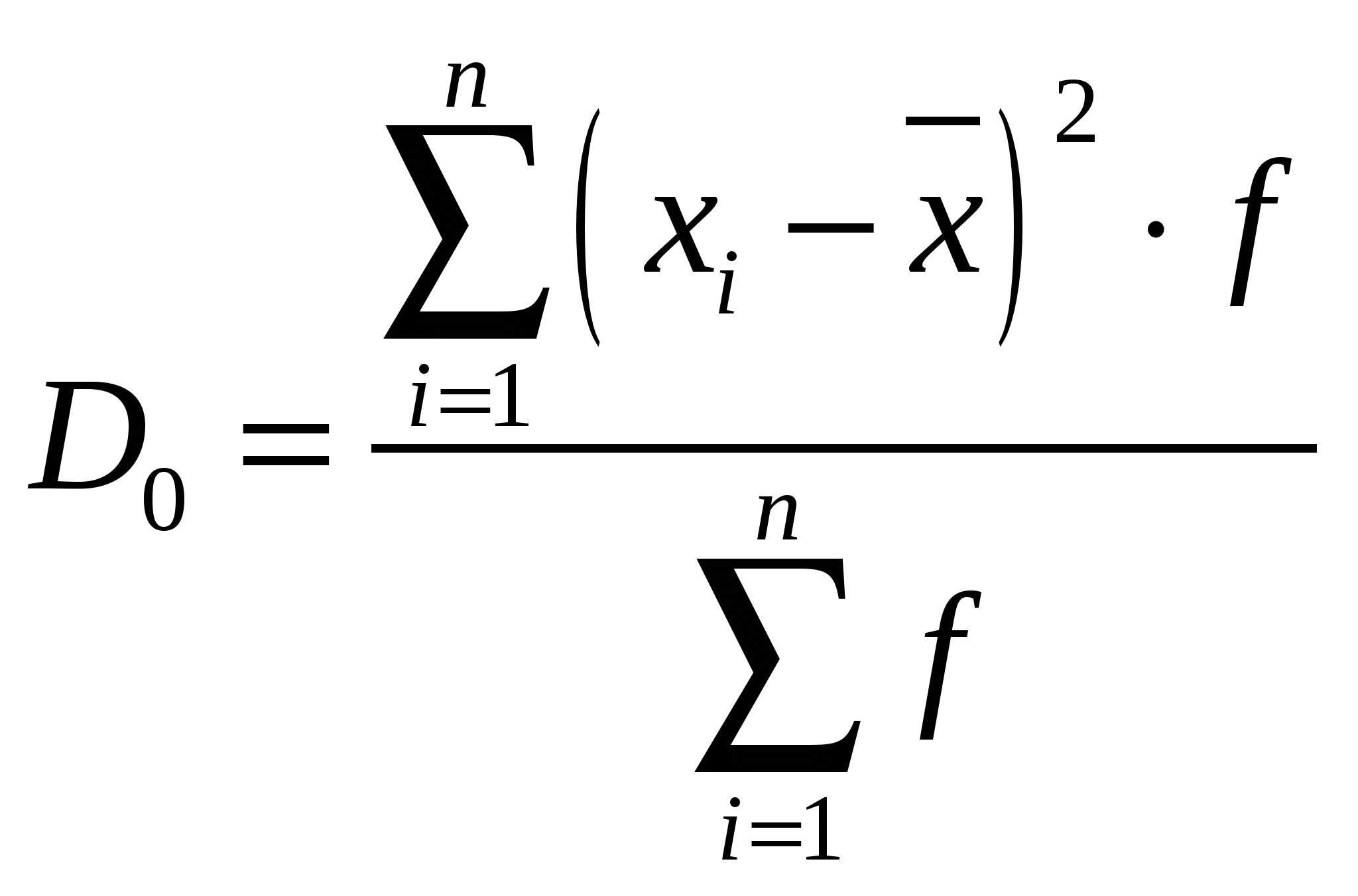

Если ставится задача выделить в составе общей дисперсии ту ее часть, которая обусловлена влиянием какого-либо одного фактора, то следует разбить совокупность данных на интервалы, положив в основу группировки этот фактор.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки характеризует межгрупповая дисперсия. Она вычисляется по формуле: , где

- частное среднее по i группе; - численность i группы.

Вариацию, обусловленную влиянием всех прочих факторов характеризует в каждой группе внутригрупповая дисперсия: , где - средняя для i группы; - число наблюдений, попавших в i группу.

Каждую группу характеризует внутригрупповая дисперсия, а по совокупности в целом средняя из внутригрупповых дисперсий: .

Между рассматриваемыми видами дисперсии существует определенное соотношение, которое называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии: .

Рассчитав эти дисперсии можно судить о силе влияния группировочного признака на образование общей дисперсии.

Если разделить межгрупповую дисперсию на общую дисперсию, получим показатель, который называют коэффициентом детерминации: .

Он показывает, какая доля всей вариации результативного признака обусловлена признаком, положенным в основание группировки.

Корень из коэффициента детерминации дает корреляционное отношение: .

Смысл этого показателя – показывать тесноту связи между группировочным признаком и результативным признаком.
18. Относительные показатели вариаций: коэффициенты вариации.

Кроме абсолютных показателей вариации рассчитывают также относительные показатели вариации – коэффициенты вариаций: .

Коэффициент вариации измеряется в процентах. Он используется для сравнения размеров вариаций в рядах с равной величиной средней, а также для сравнения вариаций разных показателей в одной и той же совокупности.

Коэффициент вариаций в известной степени является характеристикой однородности совокупности. Совокупность считается однородной, если коэффициент вариаций не превышает 33%. Большее значение коэффициента вариаций означает, что характеризует рассматриваемую совокупность по признаку, который существенно изменяется у отдельных ее единиц. Типичность такой средней не велика.
19. Закономерности распределения. Кривые распределения.

Во многих вариационных рядах можно заметить определенную связь в изменении частот и значений варьирующего признака . Такого рода закономерное изменение частот в вариационных рядах называют закономерностями распределения. Одна из важных задач анализа вариационных рядов – выявить закономерность распределения и определить ее характер. Закономерности распределения явственно проступают в массовом наблюдении, поэтому основной путь выявления закономерностей распределения – построение вариационных рядов для достаточно больших совокупностей. Кроме того, важное значение имеет правильное построение самого вариационного ряда, т.е. определение такого числа групп и размера интервалов ряда, при которых закономерности распределения проявляются наиболее отчетливо.

Исследования закономерностей распределения связано с решением двух последовательных задач:

1. Выравнивание фактического (эмпирического) распределения, которое состоит в том, что на основании фактического распределения подбирается теоретическая кривая y = f(x);

2. Проверка соответственно выбранного теоретического распределения к фактическому.

Первоначальные представления о фактической форме распределения дают графики – полигон, гистограмма.

Опираясь на фактические данные, а также на анализ сущности изучаемого явления, подбирают теоретическую кривую распределения.

Теоретической кривой распределения называют графическое изображение в виде плавной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов x_i.
20. Нормальное распределение. Особенности кривой нормального распределения.

В практике статистических исследований в качестве теоретического распределения чаще других используется нормальное распределение. Кривую нормального распределения правомерно использовать для выравнивания в тех случаях, когда на величину изучаемого признака оказывает влияние большое число полученных факторов, которые действуют независимо друг от друга и ни один из этих факторов не имеет преобладающего влияния над другим.

Уравнение нормального распределения: .

- ордината кривой нормального распределения (частости).

Нормированное отклонение: .

Т.о., кривая нормального распределения может быть построена по двум параметрам: средняя арифметическая ; среднее квадратическое отклонение .

Особенности кривой нормального распределения:

1. Кривая симметрична, поэтому в ней средняя, мода и медиана совпадают: ;

2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности;

3. Кривая имеет 2 точки перегиба, находящиеся на расстоянии от среднего значения признака: ;

4. В промежутке находится 68,3% всех значений признака; в промежутке - 95,4%; в промежутке - 99,7%.
21. Выравнивание фактического распределения по кривой нормального распределения.

Оно связано с выполнением следующих действий:

1. Для рассматриваемого вариационного ряда рассчитывают среднюю арифметическую и среднеквадратическое отклонение;

2. Для каждого вариационного ряда (середины каждого интервала) вычисляют его нормированное отклонение: .

3. Зная нормированное отклонение определяют значение функции плотности нормального распределения : ;

4. Для каждого варианта рассчитывают теоретическую частоту по формуле: , где n – общее число наблюдений; i – величина интервала.
22. Критерий согласия Пирсона.

Для проверки близости фактического и выбранного теоретического распределений вырабатывают различные критерии согласия. Наиболее распространенным является критерий Пирсона X² (Хи в квадрате).

.

Затем по специальной таблице определяют табличные значения , при выбранном уровне значимости и числе степеней свободы , где n_r – число выделенных в ряду групп; m – число характеристик теоретического распределения, принятых равными соответственным фактическим.

Для нормального распределения m = 2.

Если фактическое значение X²<табличного значения , то отклонение фактических частот от теоретических можно считать случайным, а фактическое распределение можно считать близким к выбранному теоретическому.
23. Критерий согласия Колмагорова.

Для проверки близости фактического и выбранного теоретического распределений вырабатывают различные критерии согласия. Наиболее распространенным является критерий Пирсона.

Существуют и другие критерии согласия, например А.Н. Колмагорова.

Критерий согласия Колмагорова оценивает близость фактического и теоретического распределений путем сравнения частот в вариационном ряду. При этом для каждого варианта х (интервала) ряда сначала подсчитываем величину накопления фактических и теоретических частот. Затем находят разности между ними без учета знака . Критерий согласия Колмогорова вычисляют как отношение максимального из этих разностей d_i и корня из числа наблюдений n . По найденному значению в специальной таблице находят соответствующую величину вероятности P(). С этой вероятностью можно утверждать, что отклонения фактических частот от теоретических, являются случайными. Если эта вероятность велика, то теоретическое распределение выбрано удачно.
24. Показатель асимметрии распределения.

При изучении распределения отличных от нормального возникает необходимость количественно оценить эти различия, с этой целью вычисляют показатели асимметрии и эксцесса.

Показатель асимметрии является количественной характеристикой несимметричности распределения. Коэффициент асимметрии рассчитывается по формуле, m₃- центральный момент 3-го порядка, - среднеквадратичное отклонение.. Положительная величина А_s указывает на наличие правосторонней асимметрии. Отрицательное значение А_s указывает на наличие левосторонней асимметрии . Чем больше абсолютная величина коэффициента асимметрии А_s, тем больше степень скошенности распределения.

Только для симметрических распределений рассчитывается показатель эксцесса. А_s=0.
25. Показатель эксцесса распределения.