Шпоры. 1. Предмет и задачи статистики
 Скачать 0.57 Mb.
|
 .Это позволяет упростить исходные системы уравнений. 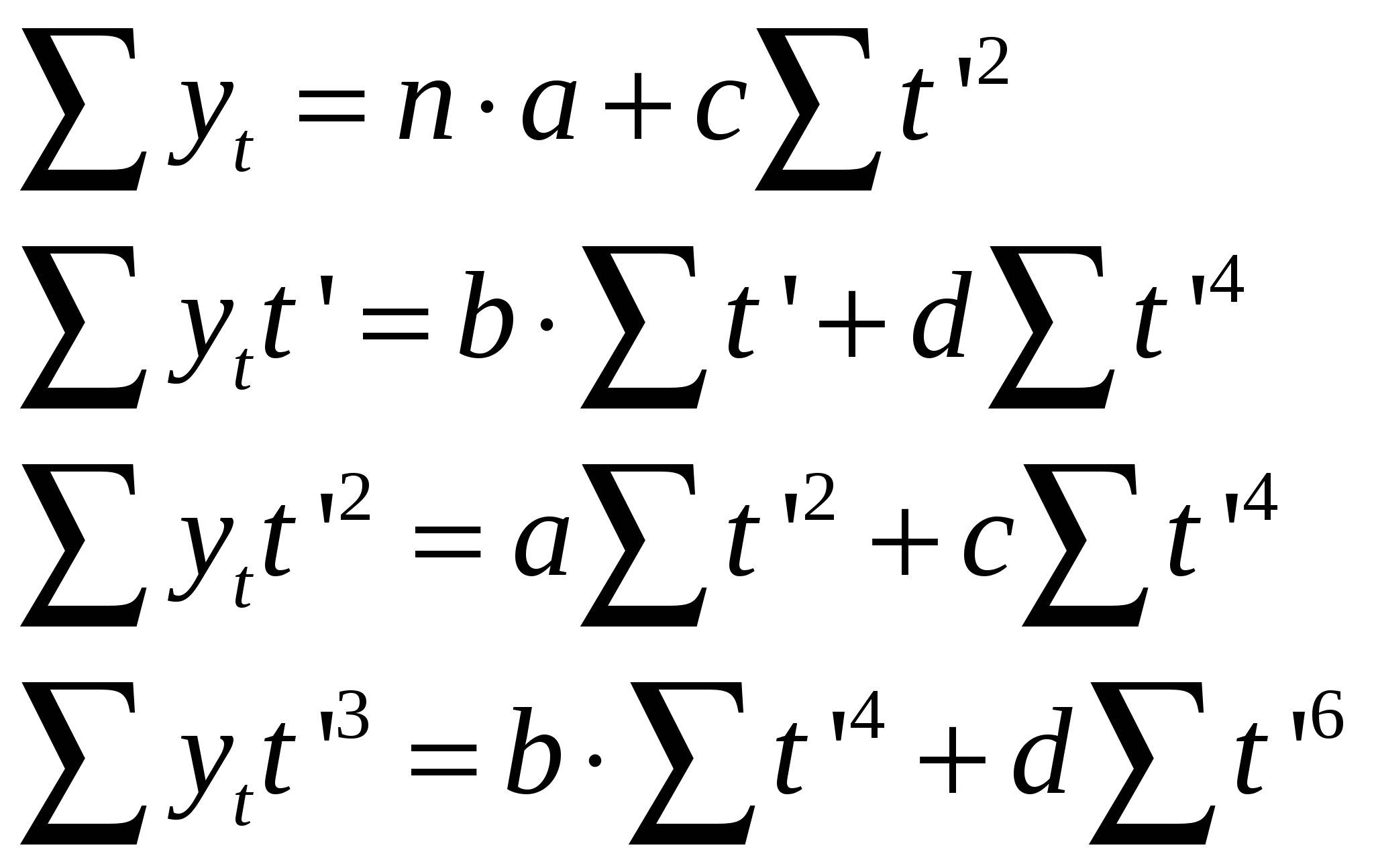 - для полинома 1 степени. - для полинома 2 степени. - для полинома 3 степени.Решая полученные системы уравнений в общем виде, можем вывести формулу для оценки параметров полиномов.  ,  - для полинома 1 степени. , ,  - для полинома 2 степени.,  , ,  - для полинома 3 степени.40. Измерение сезонных колебаний. К сезонным относят те явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодовых изменений уровней. Более менее устойчиво повторяющиеся из года в год колебания уровней динамического ряда называют сезонными колебаниями. Пример, потребление электроэнергии, перевозки пассажирским транспортом. Сезонность отрицательно влияет на результаты производственной деятельности, т.к. приводит к неравномерному использованию оборудования и трудовых ресурсов, неравномерной загрузке транспорта. Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Несколько лет рассматривают для того, чтобы получить устойчивый результат, на котором бы не отражались случайные условия отдельных лет. Для характеристики сезонных колебаний рассчитывают индексы сезонности. 1. Если динамический ряд не содержит явно выраженной тенденции к росту или снижению уровней, то индекс сезонности рассчитывается как отношение фактических помесячных уровней к среднегодовому месячному уровню уt/угод. 2. Если в ряду обнаруживается определенная тенденция развития, то индексы сезонности вычисляют как отношение фактических помесячных выровненных уровней  .Откладывая сов-ти индексов сезонности на графике в виде точек и соединяя их отрезками получим графическое изображение сезонной волны. Пример – объемы пассажирских перевозок летом больше. 41. Интерполяция и экстраполяция. Интерполяция- приближенный расчет недостающих уровней внутри однородного периода, когда известны уровни, лежащие по обе стороны неизвестного. Экстраполяция- приближенный расчет недостающего уровня, когда известны уровни, лежащие только по одну сторону неизвестного. Для интерполяции область применения – расчет в таблицах. Как экстраполяция, так и интерполяция должны проводиться лишь в пределах однородных периодов времени, в которых действует одна и та же закономерность развития. Для приблизительного расчета недост. уровня можно использовать простейшие показатели динамики (абсол. приросты, темпы роста, средний абсол. прирост, средний темп роста). Если в ряду нет резких колебаний, то интерполяцию можно произвести по смежным значениям абсолютного прироста или темпов роста. При наличии в ряду значительных колебаний лучше использовать средние показатели. Экстраполировать можно и с помощью аналитического уровня, полученного в результате выравнивания динамического ряда. В этом случае важно правильно решить вопрос по базе экстраполяции, т.е. продолжительности периода, закономерность которого можно распространить на будущие. Накопленный опыт показывает, что величина периода упреждения l не должна превышать третью часть величины базы экстраполяции n,  .42. Изучение взаимосвязей: функциональные связи. При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков. Их называют факторными признаками Признаки, которые являются результатом влияния этих факторов, зависят от них, называют результативными. Например, при изучении зависимости между показателями производительности и квалификации рабочих 1-й является результативным, а 2-й - факторным признаком. Рассматривая зависимости между признаками, выделяют два вида связи: функциональную и корреляционную. Функциональная связь характеризуется взаимнооднозначным соответствием между изменением факторного и результативного признака. При функциональной связи каждому значению факторного признака соответствует одно вполне определенное значение результативного признака. Функциональная связь обычно выражается формулами. Чаще всего такие связи наблюдаются в точных науках, главным образом в математике и физике. Например, площадь круга - результативный признак - прямо пропорциональна его радиусу - факторному признаку: S=Н*R2. Функциональная связь имеет место и в экономических процессах, но довольно редко. Например, зарплата рабочего при повременной оплате равна произведению дневной ставки на отработанное им время. Функциональную связь можно выразить уравнением y=f(x), где f(x) - известная функциональная связь этих признаков. Функциональная зависимость с одинаковой силой проявляется у всех единиц совокупности. Значит, установив на основе единичного исследования эту зависимость, мы можем пользоваться ее в любых аналогичных случаях. В зависимости от направления действия функциональные связи могут быть прямыми или обратными. При прямой связи с увеличением признака х увеличивается и признак у, при обратной - с увеличением признака х признак у уменьшается. По форме связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием величины факторного признака происходит равномерное возрастание или убывание величины результативного признака. При криволинейной связи с возрастанием величины факторного признака изменение результативного признака происходит неравномерно или направление его изменения меняется на обратное. 43. Изучение взаимосвязей: корреляционные связи. При корреляционной связи между изменением факторного и результативного признака нет полного соответствия. Это значит, что при одном и том же значении факторного признака встречаются разные значения результативного признака. При этом между ними имеется такое соотношение, что с изменением факторного признака меняется средняя величина результативного признака. Другими словами, корреляционная связь состоит в функциональной связи средней величины результативного признака со значением факторного признака. Ее можно выразить уравнением:  .Корреляционная связь проявляется в среднем по всей совокупности, а не в каждой ее единице. Поэтому она требует для своего исследования массовых наблюдений. Наличие корреляционных связей характерно для процессов, складывающихся под влиянием множества действующих с различной силой и в различных направлениях причин, в том числе случайных. Поэтому корреляционные связи являются приближенными, нестрогими связями. В зависимости от направления действия корреляционные связи могут быть прямыми или обратными. При прямой связи с увеличением признака х увеличивается и признак у, при обратной - с увеличением признака х признак у уменьшается. По форме связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием величины факторного признака происходит равномерное возрастание или убывание величины результативного признака. При криволинейной связи с возрастанием величины факторного признака изменение результативного признака происходит неравномерно или направление его изменения меняется на обратное. 44. Изучение корреляционных связей: последовательность решаемых задач. Исследование корреляционных связей включает решение ряда последовательных задач: 1. Установление факта наличия связи; 2. Определение характера связи, ее направления и формы; 3. Нахождение аналитического выражения связи, т.е. построение уравнения, с помощью которого можно рассчитать среднюю величину результативного признака при данном значении факторного признака; 4. Измерение степени тесноты связи между признаками. 45. Изучение корреляционных связей: графический метод. Для первоначального ознакомления с имеющейся связью между количественными признаками применяют графический метод. В этом случае, используя данные об индивидуальных значениях результативного и факторного признаков, строят точечный график, который называют полем корреляции. При этом по оси абсцисс откладывают значения факторного признака х, по оси ординат - значения результативного признака у. По характеру расположения точек судят о направлении и силе связи. Если точки беспорядочно разбросаны по всему полю, то зависимости между двумя признаками нет. Если же они концентрируются вокруг некоторой прямой или криволинейной оси, то делают вывод о наличии корреляционной связи между признаками у и х. Корреляционное поле используется для отображения связей внутри совокупностей небольшого объема. 46. Изучение корреляционных связей: метод аналитических группировок. Этот способ используют в случаях, когда нужно выявить зависимость на примере сотен и тысяч наблюдений. Когда производят группировку, то, как бы, изолируют факторный признак, положенный в ее основание, и изучают его влияние на вариацию результативного признака. Вариация результативного признака под влиянием факторного признака проявляется в вариации групповых средних (т.е. в межгрупповой вариации). Нужно образовать такое количество групп, при котором в межгрупповой вариации в максимальной степени проявилось бы влияние группировочного признака. При установлении оптимального числа групп можно ориентироваться на следующее положение: чем больше групп можно выделить, не наталкиваясь ни на одно отклонение  от общей тенденции, тем надежнее вывод, что найденная связь не случайна и свидетельствует о действительных взаимоотношениях между изучаемыми признаками.На базе аналитической группировки эта задача может быть решена путем расчета эмпирического корреляционного отношения:  где  Чем больше значение  приближается к 1, тем теснее зависимость между признаками. Если на график нанести точки с координатами (хс;  ),где хс -середина интервала,- соответствующая групповая средняя, и соединить их отрезками прямой, то получим так называемую эмпирическую линию связи (регрессии). 47. Изучение корреляционных связей: однофакторный корреляционно-регрессионный анализ. КРА заключается в построении и анализе статистической модели в виде уравнения регрессии (корреляционной связи), приближенно выражающей зависимость результативного признака от одного или нескольких признаков фактора. Использование КРА предполагает наличие ряда предпосылок, основными из которых являются следующие: 1. Случайность и независимость друг от друга отдельных наблюдений (единиц совокупности данных). 2. Устойчивость и независимость действия отдельных факторов. 3. Постоянство дисперсии результативного признака при изменении фактических признаков. 4. Нормальное распределение признаков. На практике перечисленные предпосылки не всегда выполняются, не смотря на это результаты КРА как правило в целом оказываются вполне удовлетворительными. 48. Однофакторный корреляционно-регрессионный анализ: выбор формы связи и оценка параметров уравнения регрессии. Для построения уравнения регрессии нужно установить теоретическую форму связи, т.е. выбрать вид функции наилучшим образом отображающий характер связи между результативным и факторным признаком. Для описания социально-экономических явлений часто используют линейную функцию (полином первой степени):  Для оценки параметров линейных по параметру уравнений можно использовать метод наименьших квадратов МНК. Система нормальных уравнений МНК выглядит следующим образом:  Решая ее способом определителей получим следующие формулы:  Параметр а1 называют коэффициентом регрессии. Он показывает, на сколько, в среднем, изменяется величина результативного признака у при изменении факторного признака на 1. Количественную зависимость между результативным и факторным признаком часто удобно выразить в относительных величинах. Для этого вычисляют коэффициент эластичности  . Он показывает на сколько в процентах изменится величина результативного признака при изменении факторного признак на 1 % относительно своей средней.Теоретические значения результативного признака получены с помощью уравнения регрессии в общем случае не совпадут с его фактическими значениями, т.е.:  , где Е - случайная составляющая.Общую дисперсию результативного признака у можно представить в виде суммы 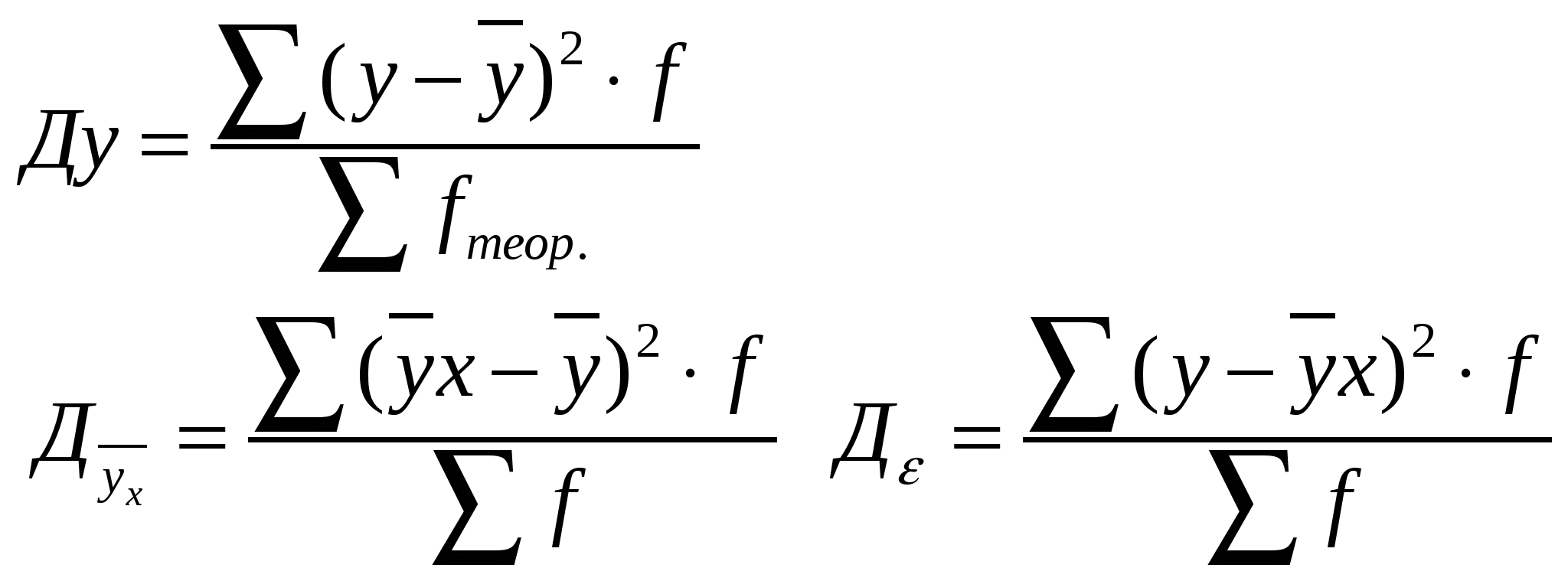 , где Дуср.х - факторная дисперсия, характеризующая вариацию у только под влиянием факторного признака. ДЕ - остаточная дисперсия, характеризующая вариацию у под влиянием всех прочих причин. Чем сильнее факторный признак влияет на результативный, тем в большей степени величина факторной дисперсии приближается к величине общей. 49. Оценка тесноты связи между признаками: индекс корреляции. На соизмерение этих величин построим индекс корреляции, измеряющий тесноту связи между признаками:  , 0Индекс корреляции пригоден для измерения тесноты связи при любой её форме то есть как линейной так и криволинейной. По разным функциям выравнивание значения у можно выбрать лучшую, которая даёт лучшие значения индекса корреляции, по критерию маx nт. 50. Оценка тесноты связи между признаками: линейный коэффициент корреляции. Частным случаем индексом корреляции является линейный коэффициент корреляции, используемый для измерения тесноты только линейной формы связи.  Его можно привести к другому виду, который дает наименьшую ошибку:  Зная величину r можно определить параметры уравнения регрессии не решая систему уравнения по формуле: 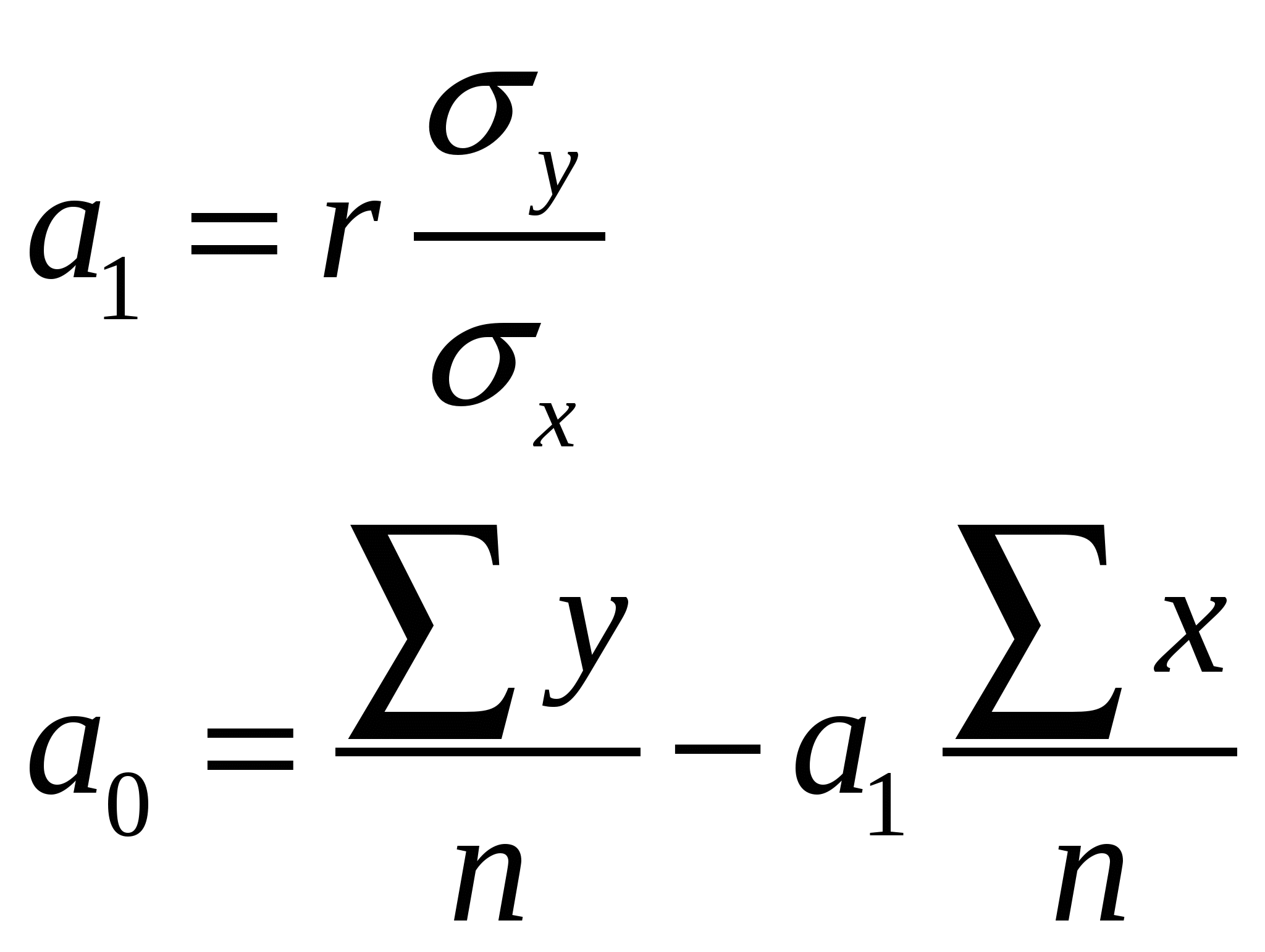 В отличии от индекса корреляции линейный коэффициент корреляции показывает не только тесноту, но и направление связи. Он может принимать значение –1< r<1. При линейной форме связи между признаками значения индекса корреляции и линейного коэффициента должны совпасть n=r. Не совпадение этих величин говорит о том, что между изучаемыми признаками криволинейная (не линейная) связь. Соизмерение их значений используют для оценки формы связи. Если их разность n-r<=0,1, то гипотеза о линейной форме связи между рассматриваемыми признаками может быть принята. 51. Изучение корреляционных связей: многофакторный корреляционно-регрессионный анализ. Многофакторный регрессионно - корреляционный анализ предусматривает построение и анализ уравнения множественной регрессии, приближенно выражающей зависимость результативного признака у от нескольких факторных признаков. При построении уравнения множественной регрессии наиболее сложным моментом является выбор типа функции. Пи выборе типа функции для многофакторной модели опираются на имеющиеся теоретические знания об изучаемом явлении, а так же на опыт аналогичных исследований. На практике наибольшее распространение получили линейное уравнение множественной регрессии вида  , где а0, а1, … - частные коэффициенты регрессии, характеризующие среднее измерение результативного признака y при изменении соответствующего факторного признака на единицу; x1, x2, … - значения факторных признаков.52. Многофакторный корреляционно-регрессионный анализ: отбор факторных признаков. На результаты многофакторного КРА существенное влияние оказывает отбор факторных признаков (x1, x2, …). Из множества возможных необходимо определить ряд факторов, учет которых, наилучшее приближение к фактическим приближениям у. Ограниченность числа наблюдений не позволяет сверх меры увеличивать количество учтенных факторов. Опыт показывает, что число наблюдений должно превосходить число включаемых в модель факторов, как минимум в 6 - 7 раз. По этому возникает задача максимального приближения к фактическим значениям y при минимальном числе включенных в уравнение факторов. В уравнение множественной регрессии следует включать факторы, которые тесно связаны с результативным признаком y, но не зависящие друг от друга. Для решения этой задачи составляется матрица парных коэффициентов корреляции.
При анализе матрицы сначала рассматривают коэффициенты корреляции результативного признака у с каждым из факторных признаков. Факторная связь, которых с у оказывается слабой исключается ил дальнейшего рассмотрения. Затем анализируют взаимосвязи факторов друг с другом и выявляют пары факторов тесно связанные между собой (r xi xj>=0,7). Такие факторы называют количественными. Из рассмотрения исключаются те из количественных факторов, влияние на у которых, наименьшее. При отборе наиболее важных факторов можно ориентироваться на величину множественного коэффициента корреляции R. Например, если имеются данные о результативном признаке и 10 влияющих на него факторов из которых надо отобрать 5, то следует предпочесть сочетания тех 5 факторов, которые соответствуют максимальным значениям. 53. Построение линейного уравнения множественной регрессии с помощью МНК. Для оценки значений частных коэффициентов регрессии (а0, а1, …) можно использовать метод наименьших квадратов. Методику расчета рассмотрим на примере линейной двухфакторной регрессии: |