Ответы на экзаменационные ответы инженерная графика. инжа. 1. Предмет инженерная графика. Требования, предъявляемые к чертежу. Метода построения изображений на чертеже
 Скачать 4.4 Mb.
|
|
1. Предмет инженерная графика. Требования, предъявляемые к чертежу. Метода построения изображений на чертеже. Инженерная графика - прикладная область знаний о разработке конструкторской документации. Объектом изучения инженерной графики является изучение геометрических свойств объектов.  Требования к чертежу:Наглядность Удобоизмеряемость Методы проекций: Параллельные: Косоугольные Ортогональные ( прямоугольные) Центральные 2. Параллельное проецирование. Инвариантные свойства параллельного проецирования. Если проецирующие лучи параллельны друг другу, а центр проецирования удален в бесконечность, то такое проецирование называется параллельным. Свойства параллельного проецирования: 1. Изображения точки есть единственная точка. 2. Непрерывность линии между двумя точками сокращается на изображение линии между теми же точками. Следствие: если точка принадлежит линии, то проекция этой точки принадлежит проекции этой линии. 3. Изображение прямой есть прямая. 4. Отношение, в котором точка отрезка делит отрезок одинаково в изображении и в оригинале. Следствие: середина отрезка изображается серединой его проекции. 5. Проекции параллельных прямых параллельны. 6 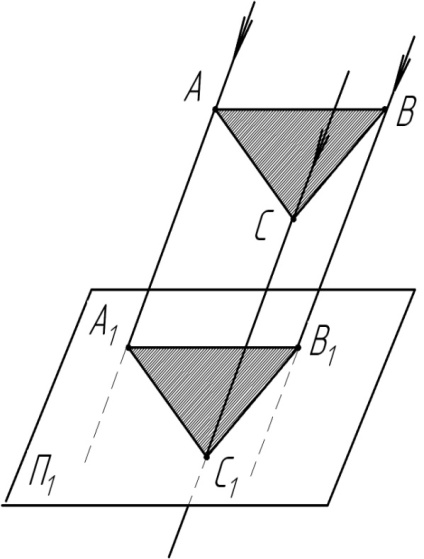 . Элементы объекта, лежащие в плоскости, параллельно плоскости проекции, изображается на ней без искажений.3. Центральное проецирование Методом проецирования называется способ получения изображений с помощью определенной, присущей только ему совокупности средств проецирования (центра проецирования, направления проецирования, проецирующих лучей, плоскостей (поверхностей) проекций), которые определяют результат — соответствующие проекционные изображения и их свойства. 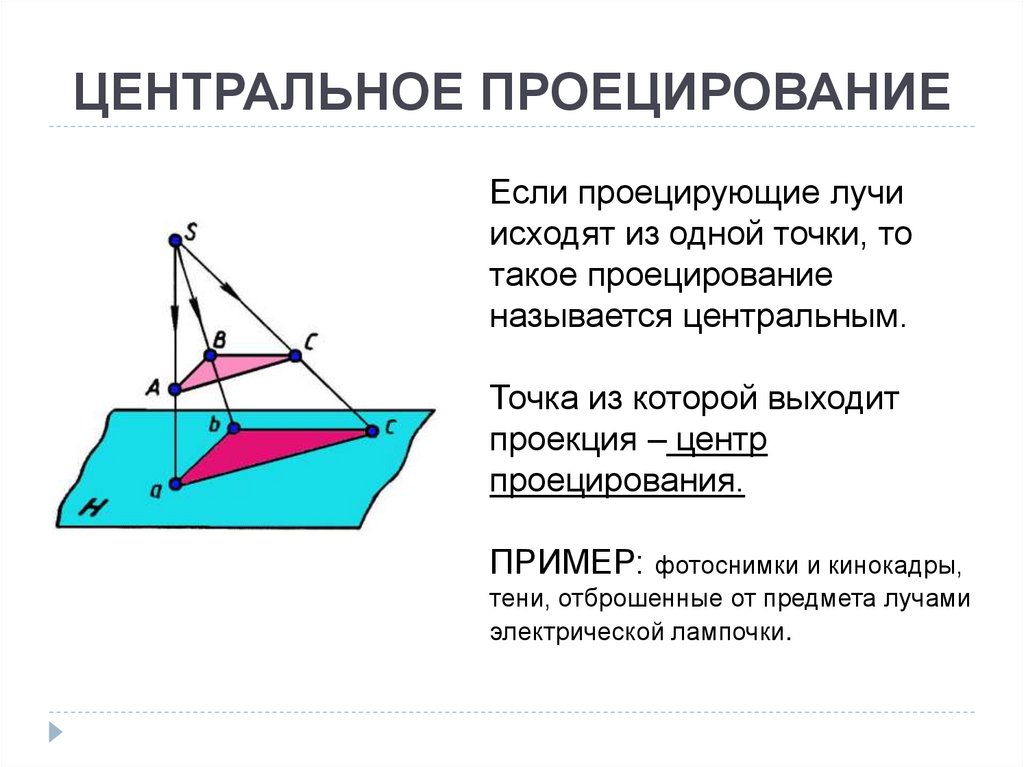 4. Плоскости уровня. Плоскости общего положения. Плоскости уровня - плоскости параллельные плоскости проекции. Свойство: одна проекция - истинная величина, две других отрезки прямых. Плоскость параллельная горизонтальной плоскости проекции называется горизонтальной плоскостью уровня. Плоскость параллельная фронтальной плоскости проекции называется фронтальной плоскостью уровня. Плоскость параллельная профильной плоскости проекции называется профильной плоскостью уровня. 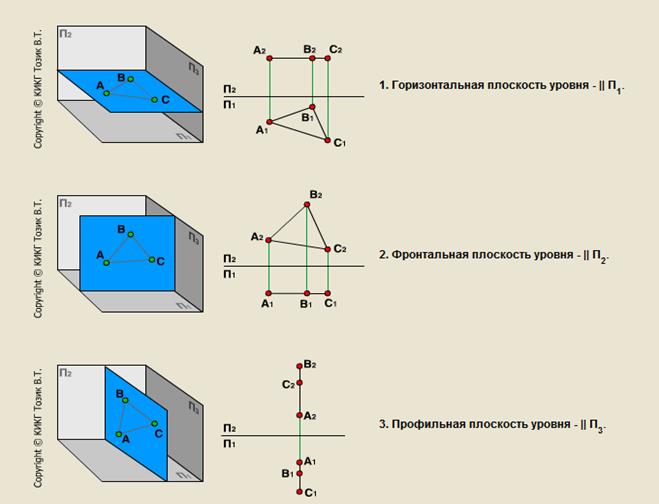  5. Проецирующие плоскости. Плоскости общего положения. Проецирующие плоскости - плоскости перпендикулярные одной плоскости проекции. Свойство: отображается отрезком прямой на той плоскости, которой перпендикулярна. На двух других изображается в искаженном виде, но сохраняет геометрическую форму. Плоскость перпендикулярная горизонтальной плоскости проекции называется горизонтально-проецирующей плоскостью. Плоскость перпендикулярная фронтальной плоскости проекции называется фронтально-проецирующей плоскостью. Плоскость перпендикулярная профильной плоскости проекции называется профильно-проецирующей плоскостью. 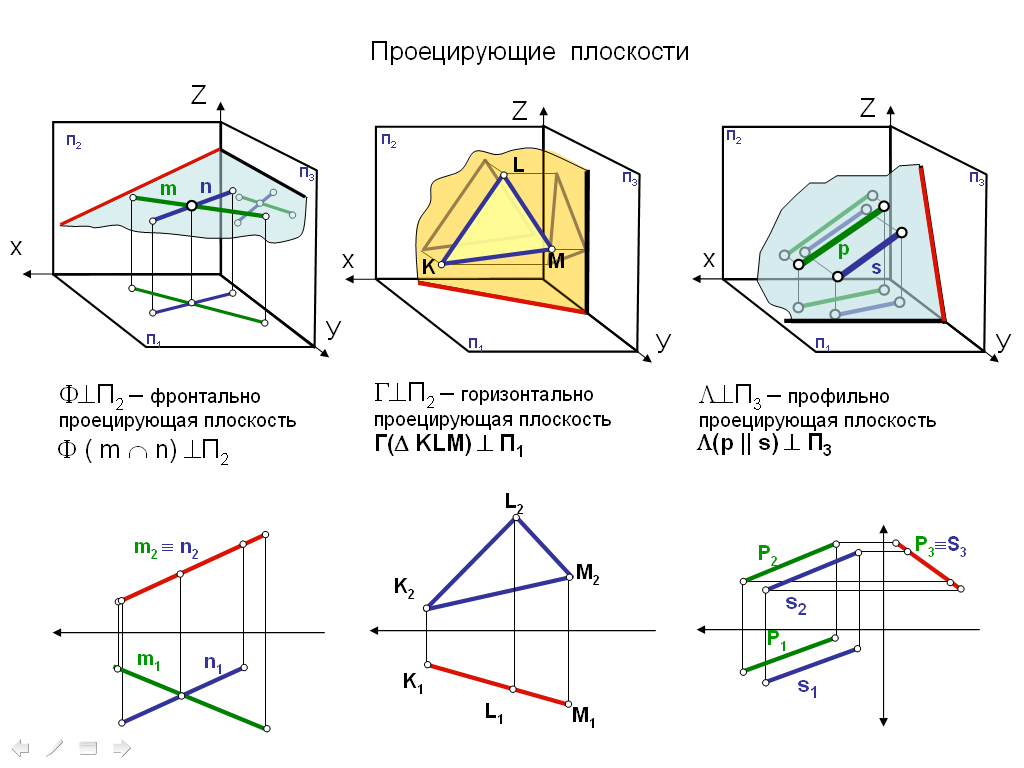 6. Прямые уровня Прямые уровня – прямые, параллельные одной из плоскостей проекции и наклонные к двум другим. Свойства: Одна проекция – истинная величина, две другие – отрезки прямых, параллельные осям. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции параллельны осям проекций. Если прямая перпендикулярна плоскости проекции, то ее проекцией на эту плоскость является точка, а вторая проекция, перпендикулярная осям проекций. Прямые уровня: Горизонтальная прямая – прямая параллельная горизонтальной плоскости проекций. Фронтальная прямая- прямая параллельная фронтальной плоскости проекций. Профильная прямая –прямая параллельная профильной плоскости проекций. 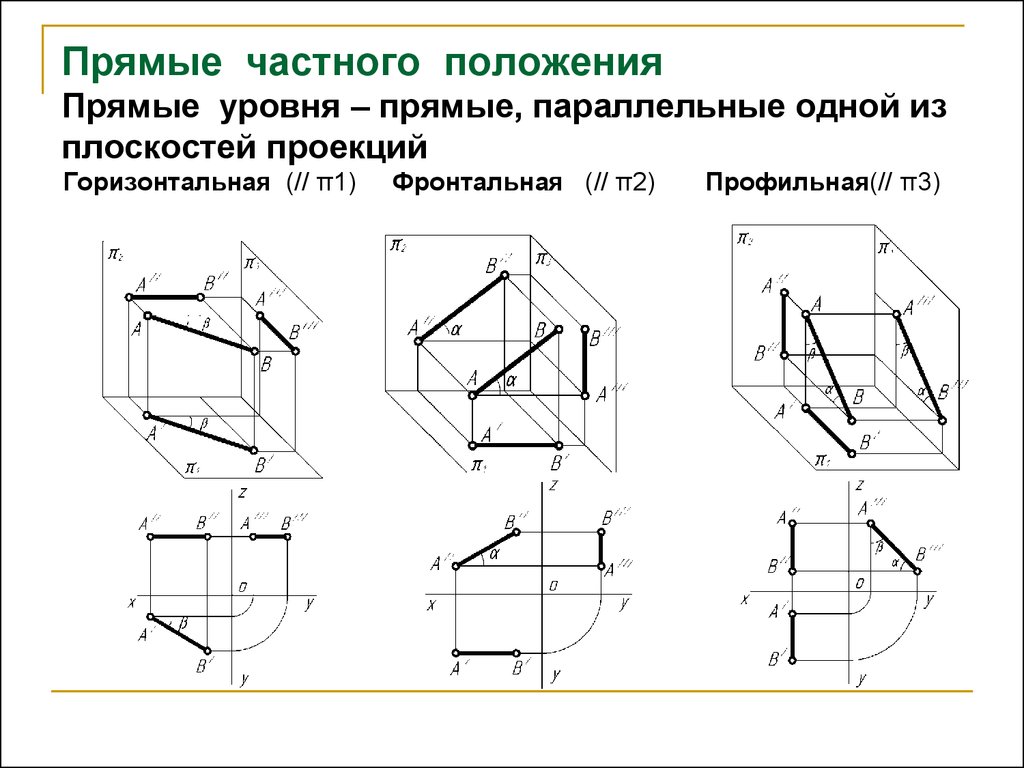 7. Проецирующие прямые Проецирующие прямые – прямые перпендикулярные какой-либо плоскости проекции. Свойства: 1)Две проекции – истинная величина, на третьей плоскости проекции прямая проецируется в точку, так как она перпендикулярна плоскости проекции. Проецирующие прямые: Горизонтально проецирующая прямая – прямая перпендикулярная горизонтальной плоскости проекции. Фронтально проецирующая прямая – прямая перпендикулярная фронтальной плоскости проекции. Профильно - проецирующая прямая – прямая перпендикулярная профильной плоскости проекции.  8. Виды. Основные и дополнительные виды. Понятие главного вида и схема расположения видов. Вид - ортогональная проекция, обращенная к наблюдателю в видимой части поверхности предмета, расположенная между ним и плоскостью проецирования. (ГОСТ 2.305 - 2008) Дополнительный вид получается проецированием предмета на плоскость не параллельную ни одной из плоскостей проекции. Применяется в случаях, когда отдельные плоскости проецируются с искажением. Обозначается буквами русского алфавита, а у связанного с ним основного вида ставится стрелка, указывающая направление проецирования. Виды: 1. Вид спереди 2. Вид сверху 3. Вид слева 4. Вид справа 5. Вид снизу 6. Вид сзади Основные виды: спереди, сверху, слева. Главный вид - вид, который дает наибольшую информацию о форме и размерах предмета.  9. Виды. Требования ГОСТ 2.305-2008 к расположению видов Виды: 1. Вид спереди 2. Вид сверху 3. Вид слева 4. Вид справа 5. Вид снизу 6. Вид сзади 10. Дополнительный вид. Порядок построения. Обозначение дополнительных видов. Дополнительный вид получается проецированием предмета на плоскость не параллельную ни одной из плоскостей проекции. Применяется в случаях, когда отдельные плоскости проецируются с искажением. Обозначается буквами русского алфавита, а у связанного с ним основного вида ставится стрелка, указывающая направление проецирования. 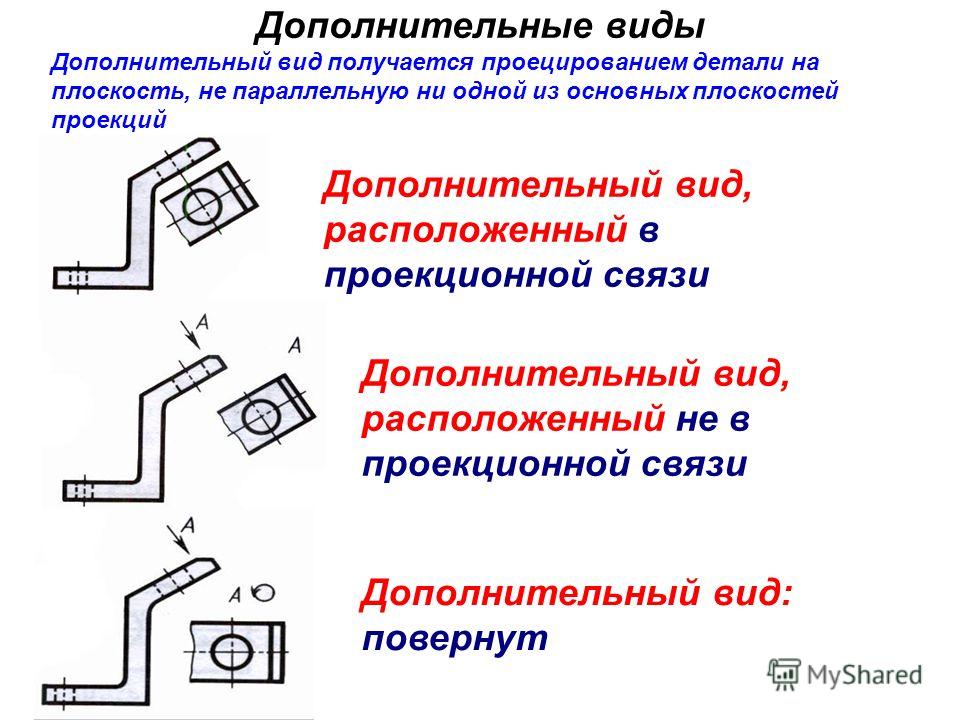  Алгоритм построения: 1) Найти вид, где плоскость будет проецироваться в отрезок прямой. 2) Отметить характерные точки; отметить проекции точек на другом изображении. 3) Провести линии проекционной связи перпендикулярно проекции плоскости на том виде, где она проецируется. 4) Обозначить проекции осей, закрепленных за плоскостью, на которых строим доп. вид. 5) Построить координаты характерных точек. 6) Соединить точки в логической последовательности. 11. Поверхности. Определитель поверхности. Каркасные линии поверхности Поверхность - это множество положений, образующих l, перемещающихся в пространстве по определенному закону. В качестве образующих могут использоваться прямые и кривые линии. Закон перемещения образующих может быть задан линиями другого направления. Эти линии называются направляющими (m). Образование поверхностей 1. Аналитический. Характеризует задание непрерывной поверхности. В этом случае поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют уравнению, задающему поверхность: F = (x, y, z) = 0 2. Каркасный. Берется плотный каркас линий, принадлежащих поверхности. 3. Кинематический.(Используется в инженерной графике). Кинематический. В этом случае поверхность рассматривается как совокупность последовательных положений некоторой линии, называемой образующей l, непрерывно перемещающейся в пространстве вдоль другой линии – направляющей q – по определённому закону. Такие поверхности называют кинематическими. 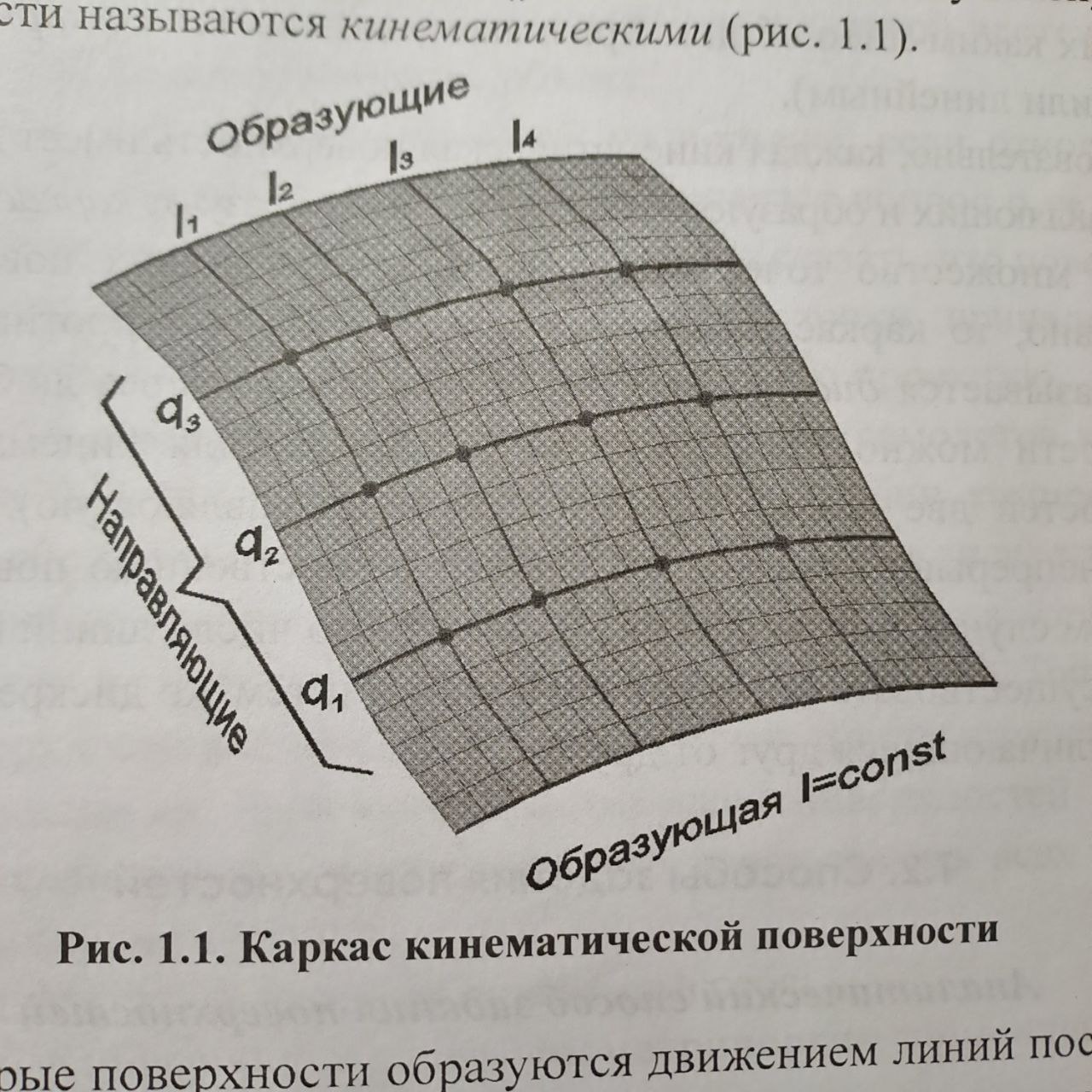 Определитель поверхности - это совокупность условий, однозначно определяющих поверхность в пространстве. геометрическая часть определителя - изображение образующей и направляющей. алгоритмическая часть определителя - устанавливает связь между геометрическими элементами. Множество точек или линий, принадлежащих поверхности и объединённых каким-либо общим признаком, называется её каркасом (точечным или линейным) 12. Классификация поверхностей. 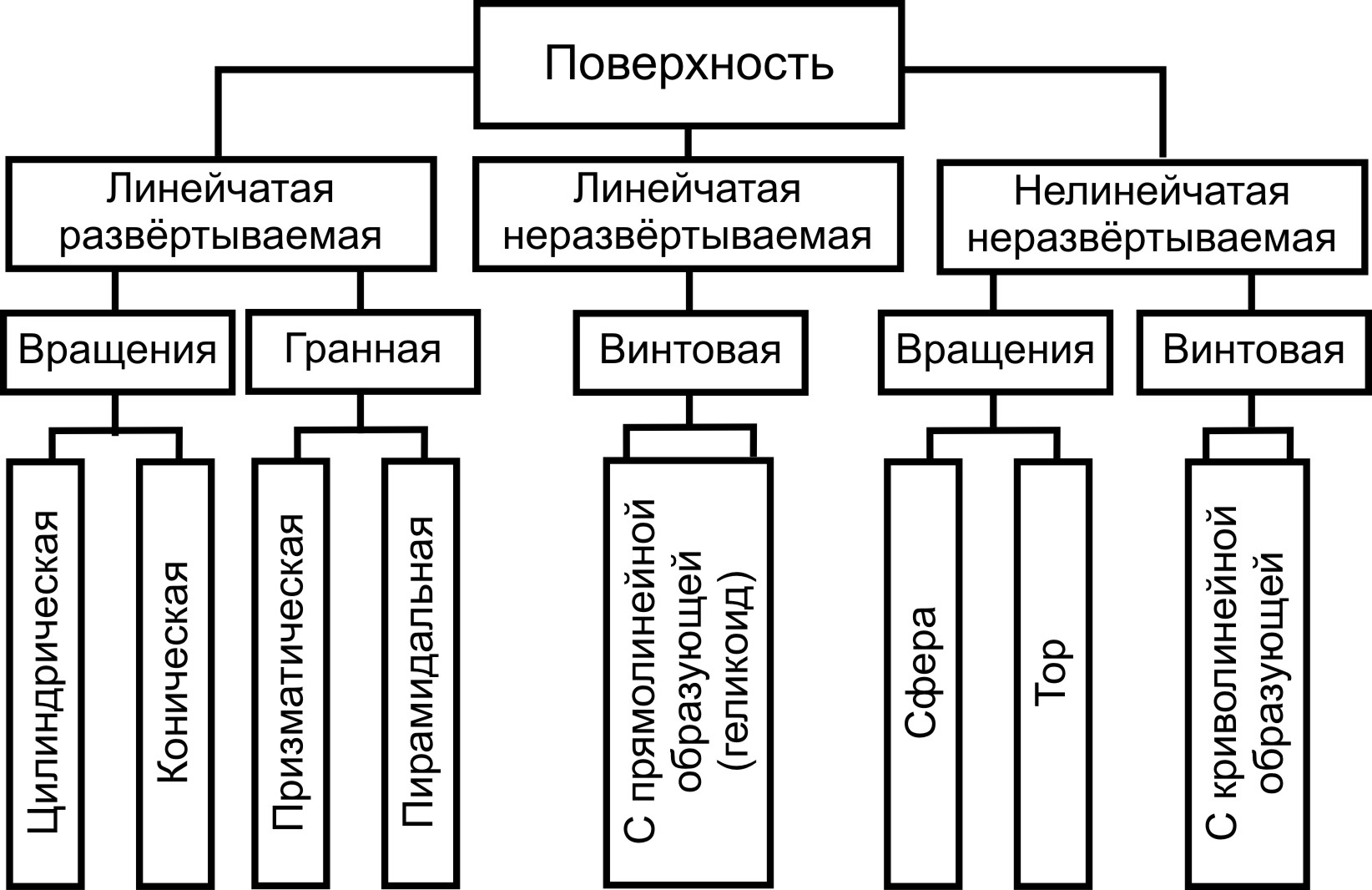 13. Поверхности вращения. Образование поверхностей вращения. Поверхности вращения – поверхность, описываемая какой-нибудь линией образующей частности прямой при ее вращении вокруг неподвижной оси. 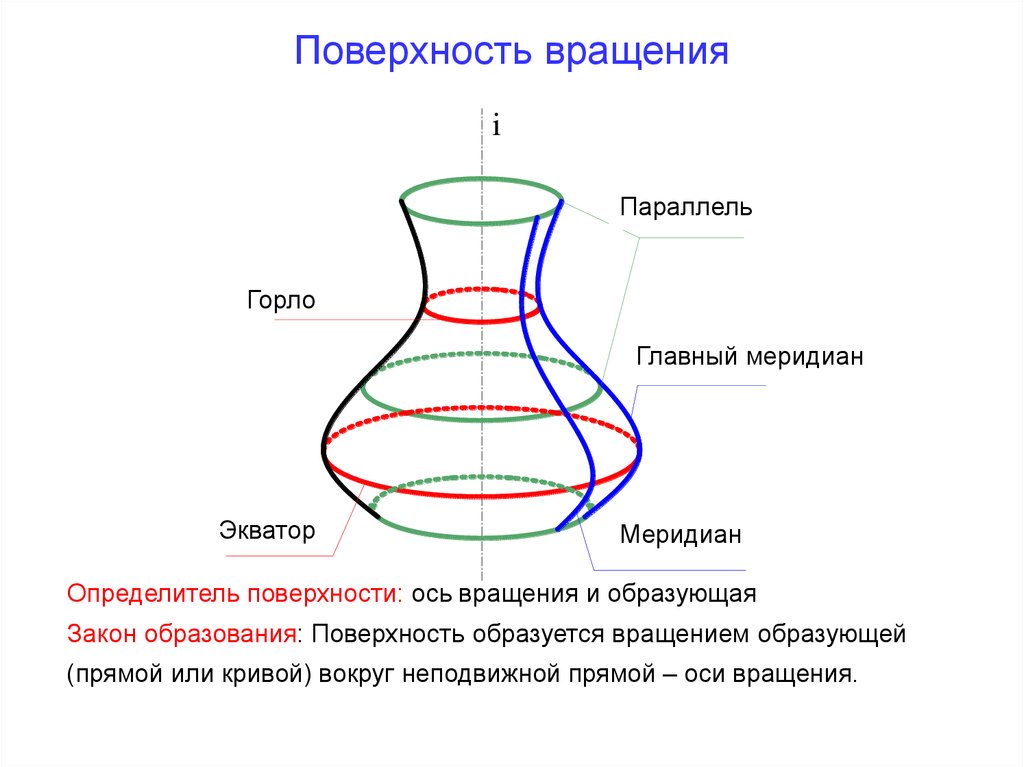 Меридиан, расположенный во фронтальной плоскости проецируется без искажений и называется главным фронтальным меридианом. Он определяет фронтальный очерк поверхности. Параллель наибольшего размера называется экватором, наименьшего - горлом. Экватор определяет горизонтальный очерк поверхности. Линейчатая поверхность: Цилиндр и конус - образующая прямая линия Нелинейчатая поверхность: Сферическая и торовая поверхность - образующая окружность. Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными основаниями (плоскостями). Конус - геометрическое тело, ограниченное конической поверхностью, которая получается при вращении прямой, закрепленной на оси, и плоскостью, пересекающей все образующие. Если ось конуса перпендикулярна основаниям, такой конус называется прямым. 14. Плоские сечения конуса. 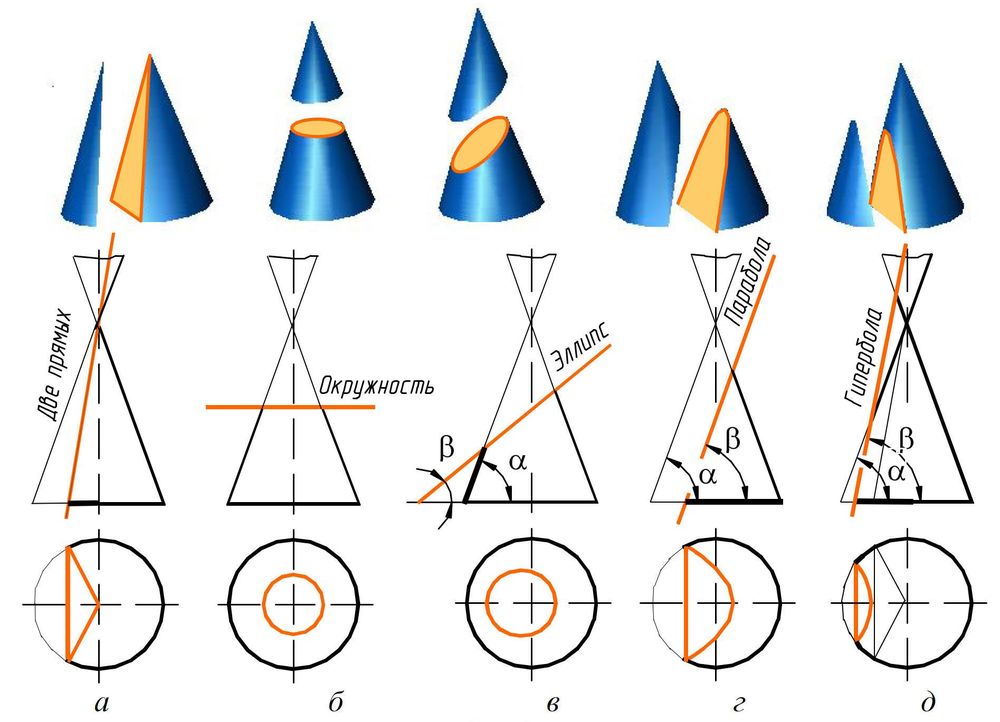 15. Основные каркасные линии сферы. Плоские сечения сферы. Сфера - поверхность, образованная вращением окрестности вокруг отрезка, являющегося ее диаметром. Экватор - окружность, которая получается пересечением сферы плоскостью перпендикулярной оси вращения и проходящей через центр сферы. Меридиан - окружность, которая получается пересечением сферы плоскостью перпендикулярной плоскости экватора и проходящей через центр сферы. 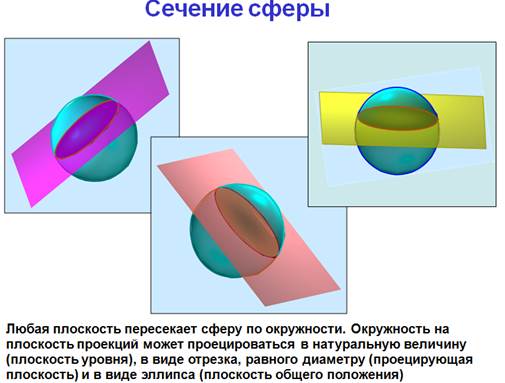 16. Определение линии пересечения двух геометрических тел (частный случай). Частный случай пересечения: Если одна из поверхностей занимает проецирующее положение, то её вырожденная проекция (своя поверхность, спроецированная в линию), включая проекцию линии пересечения Вторая проекция этой линии строится из условия принадлежности её точек не проецирующей поверхности (при помощи линии каркаса) А третья – по координатам ОСК Теорема Монжа 1. Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1). 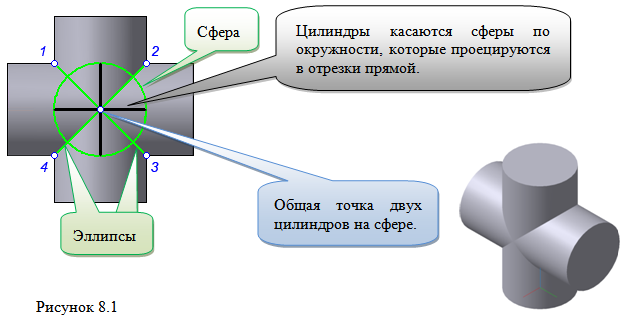 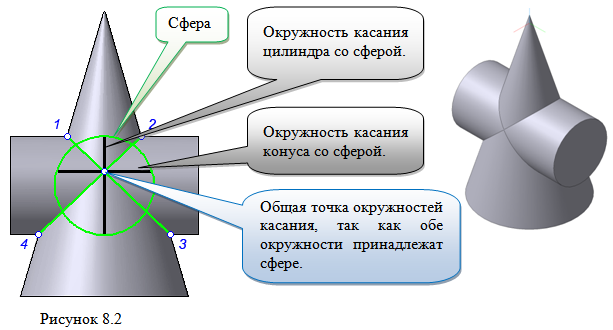 Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4. Цилиндры пересекаются по эллипсам. Крайние образующие пересекаются в точках 1, 2, 3, 4. 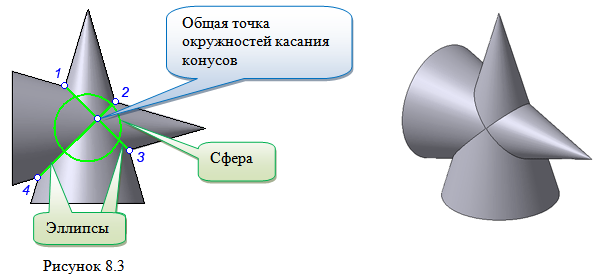 Теорема Монжа 2. Если две пересекающиеся поверхности второго порядка имеют общую плоскость симметрии, параллельную некоторой плоскости проекций, то на эту плоскость проекций линия их пересечения проецируется в кривую второго порядка. Если это условие не выполнено, то – в кривую четвертого порядка. Эту плоскость называют плоскостью параллелизма. Рассмотрим четыре примера пересечения тел вращения, у которых оси вращения лежат в одной плоскости, параллельной плоскости проекций π2 (Рисунок 8.4). Следовательно, данная плоскость является плоскостью симметрии пересекающихся тел, параллельная плоскости проекций π2. Это означает, что линия пересечений тел проецируется на плоскость проекций π2 как кривая второго порядка – парабола. 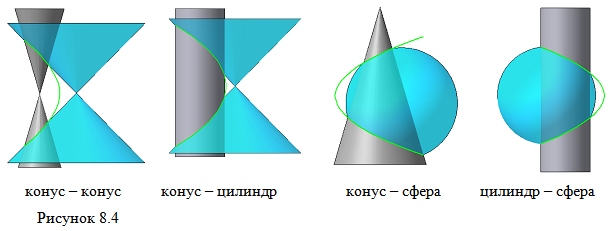 8.2. АЛГОРИТМ ПОСТРОЕНИЯ ТОЧЕК КРИВОЙ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ Выполним анализ кривых пересечения цилиндра и конуса (Рисунок 8.5): у данных тел есть общая плоскость симметрии, параллельная плоскости проекций π2, следовательно, (согласно второй теореме Монжа) на π2 кривые пересечения тел 4-го порядка проецируются в виде кривых второго порядка. Поскольку при этом получается две ветви, следовательно, это будет гипербола. Строим характерные точки: пересечение крайних образующих на π2 цилиндра и конуса, точки 1, 2, 3, 4. Для нахождения точек, лежащих на крайних образующих на π1 цилиндра, введём плоскость σ⊥π2 и σ//π1 проходящую через фронтальную проекцию оси вращения цилиндра. В результате данная плоскость пересечет цилиндр по крайним образующим, а конус – по окружности радиусом Rσ. Построенные на π1 сечения пересекутся в точках 5, 6, 7, 8. По линии проекционной связи строим их фронтальные проекции. Для построения самых близких друг к другу точек кривой на π2 введём плоскость γ⊥π3, проходящую через вершину конуса и касательную к цилиндру. Данная плоскость пересечёт конус по треугольнику SAB. Построив образующие конуса SA, SB и цилиндра 11-12, на их пересечении определим точки 11, 12. Точки 9, 10 построим симметрично точкам 11 и 12. Для построения дополнительных промежуточных точек, можно ввести вспомогательные секущие плоскости (посредники) параллельно σ. 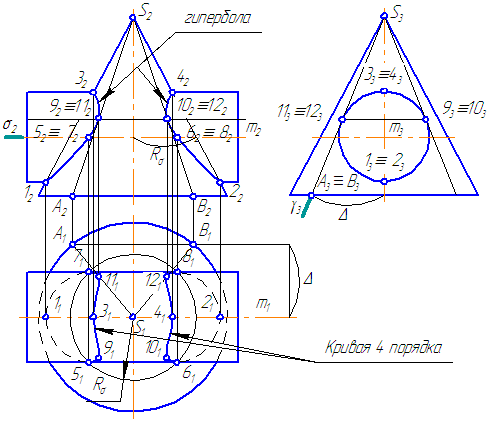 Рисунок 8.5 – Построение линии пересечения конуса и цилиндра На анимации ниже представлена последовательность построения линии пересечения конуса и цилиндра. 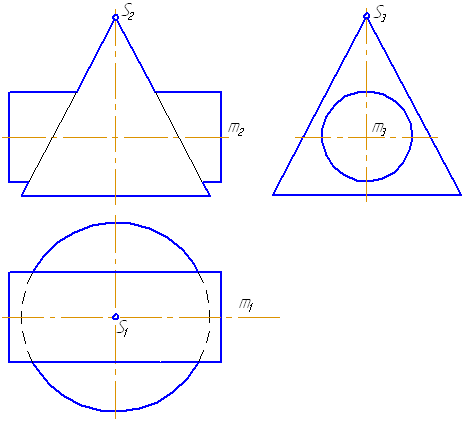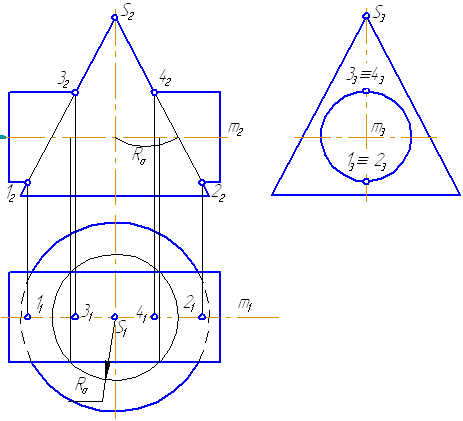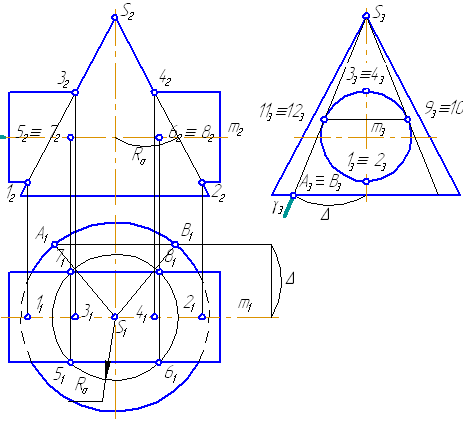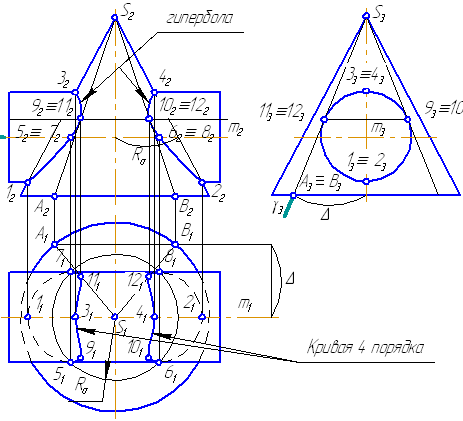 Рисунок 8.6 – Последовательность построения линии пересечения конуса и цилиндр 17. Общий случай пересечения поверхностей. Метод вспомогательных секущих плоскостей («плоскостей-посредников»).  Условие применимости: Должны быть две поверхности вращения П1 и П2, не занимающие частное положение на чертеже. Для определения линии пересечения поверхности П1 и П2 следует ввести третью (вспомогательную поверхность Ri). Оси поверхности должны быть параллельны Общие случаи пересечения двух поверхностей Оси поверхности параллельны Оси поверхности пересекаются Оси поверхности скрещиваются 18. Метод концентрических сфер. Условия применимости метода вспомогательных концентрических сфер. Метод концентрических сфер Этот способ применяется в случае, когда оси двух поверхностей вращения пересекаются под некоторым углом и находятся в плоскости, параллельной какой-либо плоскости проекций (особенно в том случае, когда на чертеже дана только одна проекция деталей). Шар со всякой поверхностью вращения, ось которой проходит через центр шара, пересекается по окружностям. Эти окружности находятся в плоскостях, перпендикулярных к оси поверхности вращения, и проецируются на одну из плоскостей проекций в виде прямых, в этом состоит преимущество способа сфер. На рисунок 124 дана фронтальная проекция шара, пересекающегося с конусом и цилиндром. Как видно, центр шара находится на пересечении осей данных поверхностей, а линии его пересечения с ними — окружности диаметров: 1 - 2, 3 - 4, 5 - 6.
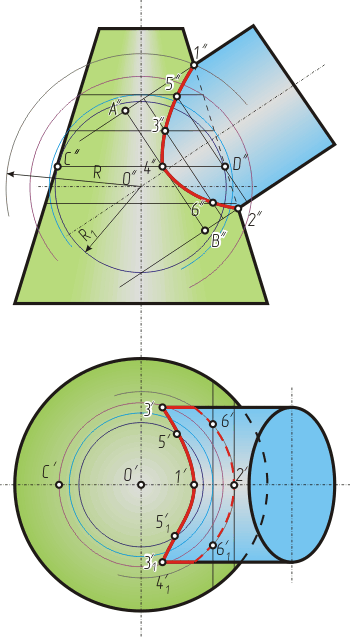
ПримерДаны конус и цилиндр, оси которых пересекаются под некоторым углом. Построить линию пересечения заданных поверхностей (рисунок 125).Наивысшую и наинизшую точки 1 и 2 линии пересечения находят непосредственно в пересечении крайних образующих на фронтальной проекции заданных поверхностей.
Для нахождения промежуточных точек 3, 4, 5, ... проводят из центра О" ряд вспомогательных концентрических сфер радиуса от R до R1 , которые рассекают заданные тела по окружностям (рисунок 125). На фронтальной проекции эти окружности проецируются в прямые линии и, пересекаясь между собой, определяют точки линии перехода. Так, для нахождения точек 3 (одна из них невидима) проводят сферу радиуса R1 , которая пересечет цилиндр по окружности диаметра A" B", конус — по окружности диаметра C"D". В пересечении указанных окружностей определяются точки 3. Горизонтальные проекции этих точек находятся на окружности (параллели конуса), проведенной из центра О' радиусом, равным C"D"/2. Все остальные промежуточные точки определяются аналогично. Так как пересекающиеся тела симметричны, их линия пересечения также симметрична. На фронтальной проекции невидимая часть линии пересечения сливается с видимой. Точки 4 (на горизонтальной проекции) служат границами раздела видимой и невидимой части линии пересечения. Найденные точки соединяют плавной кривой по лекалу с учетом видимости. Условия применимости: 1. Обе поверхности должны быть поверхностями вращения. 2. Оси поверхности должны пересекаться. 3. Плоскость, образованная пересекающимися осями, должна быть параллельна одной из плоскостей проекции Сфера мин. радиуса - это такая сефра, которая касается очерка одной поверхности и пересекает очерк другой поверхности. 19. Соосные поверхности. Теорема Монжа. Соосными называются поверхности вращения, имеющие общую ось. Соосные поверхности пересекаются по окружностям перпендикулярным оси вращения. Если 2 соосные поверхности вращения имеют одну общую точку, то они имеют одну общую параллель. Теорема Монжа Если две поверхности 2-го порядка описаны или вписаны около третьей поверхности 2-го порядка, то линии их пересечения 4-го порядка распадаются на 2 плоские линии 2-го порядка. Плоскости, полученных линий проходят через прямую, соединяющей точки пересечения, линии касания заданных поверхностей. 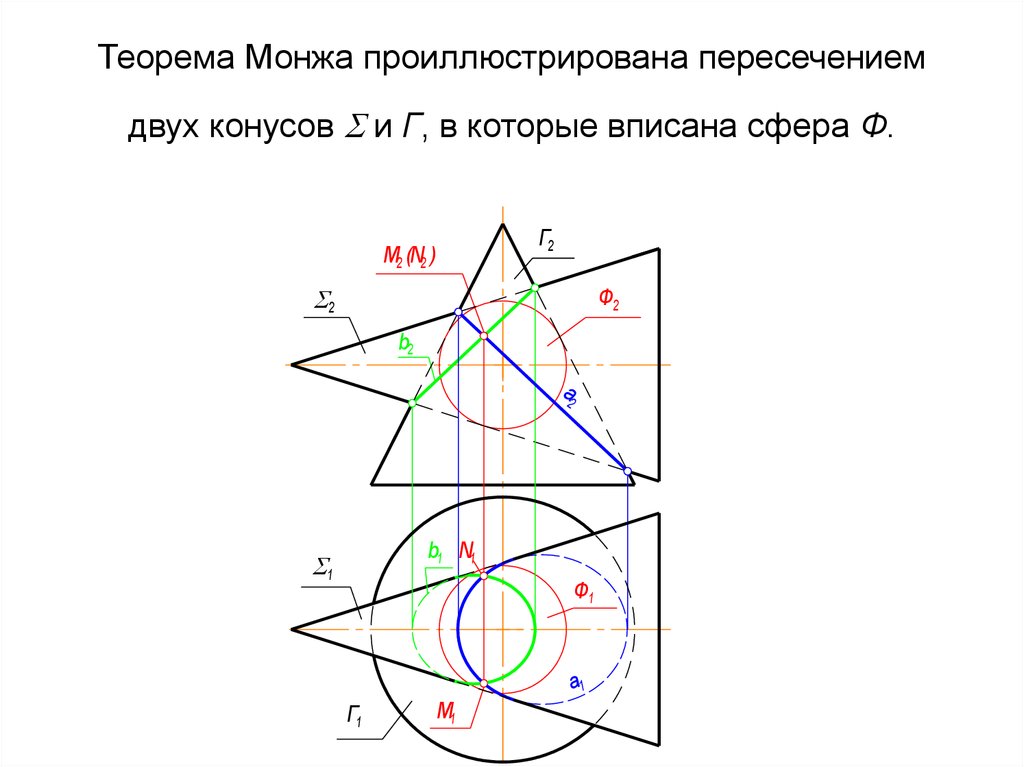 20. Cечения. Обозначение сечений. Сечения - это изображение фигуры, получающееся при мысленном сечении предмета одной или несколькими плоскостями в сечении получается то, что находится в секущей плоскости. Сечения, не входящие в разрез, разделяют на вынесенные и наложенные.   21. Вынесенные сечения. Вынесенные сечения являются предпочтительными.  Допускается в качестве секущей плоскости применять цилиндрическую поверхность, развернутую потом в плоскость.  Вынесенные сечения допускается располагать в разрыве между частями одного и того же вида.  Контур вынесенного сечения, а также сечения, входящие в состав разреза изображают сплошными основными линиями, а контур наружного сечения сплошными тонкими линиями. О  сь симметрии вынесенного или наложенного сечения указывают тонкой штрих-пунктирной линией без обозначения буквами и стрелками и линию сечения не проводят.Сечение, выполненное на продолжении следа секущей плоскости не обозначается. 22. Наложенные сечения Наложенные сечения не обозначают  Для несимметричных сечений, расположенных в разрыве или наложенных, линию сечения проводят со стрелками, но не обозначают.  Для нескольких одинаковых сечений, относящихся к одному и тому же предмету, линию сечения обозначают одной буквой и вычерчивают одно сечение 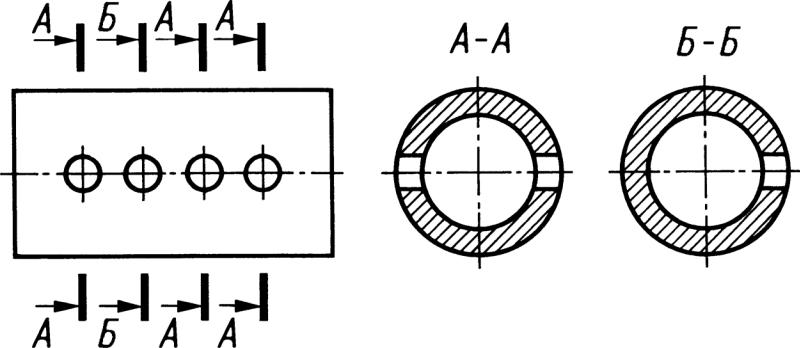 Секущие плоскости выбирают так, чтобы поперечное сечение было нормальным. Если при этом секущая плоскость направлена под различными углами, то графически обозначают «повёрнуто» Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстия или углубления, то контур поверхности или углубления показывают полностью. 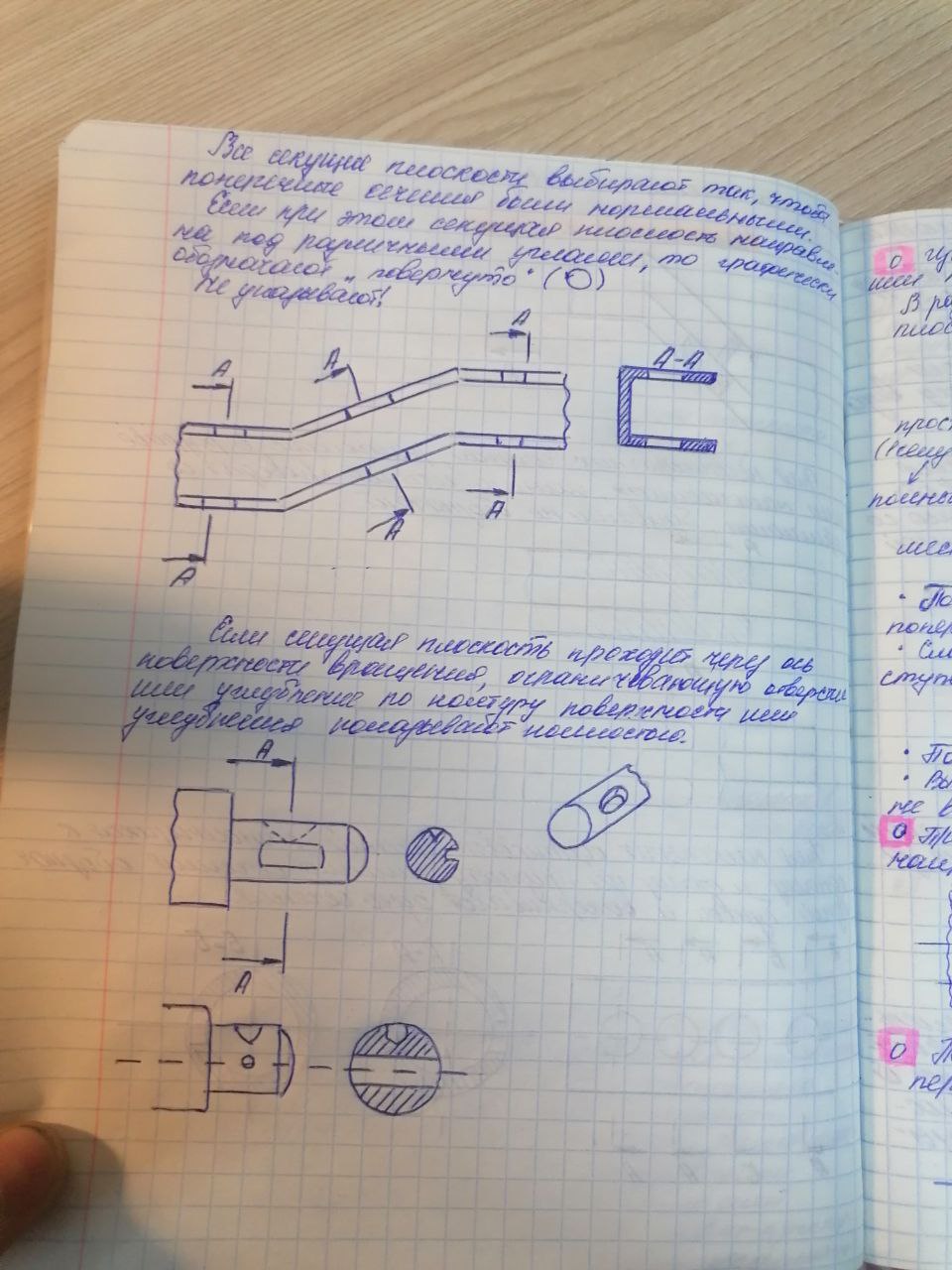 23. Определение разреза. Обозначение разрезов. Разрезом называется изображение детали мысленно рассеченной одной или несколькими плоскостями. В разрезе показывается то. что получается в секущей плоскости и то, что находится за ней. Разрез обозначается аналогично сечению. Если секущая плоскость совпадает с плоскостью симметрии детали и находится непосредственно в проекционной связи, между двумя изображения нет третьего, то данный разрез не обозначается. Если деталь симметричная, тона одном изображении можно соединить половину вида и половину разреза 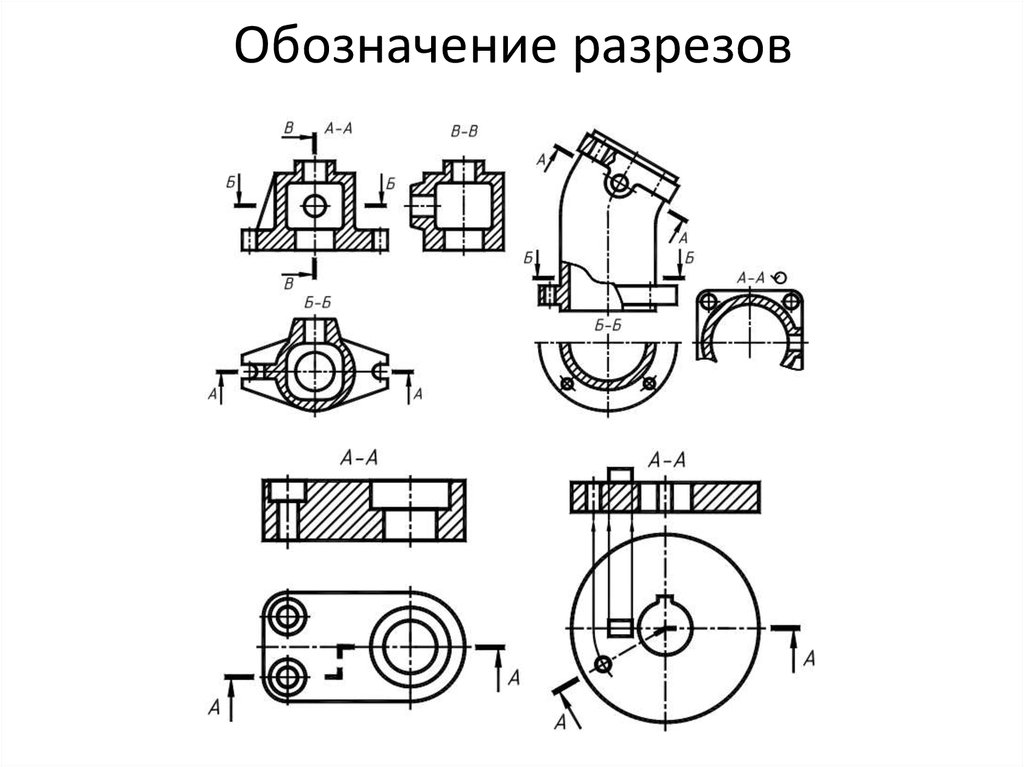 24. Классификация разрезов. Разрезы Простые Сложные (Одна секущая плоскость) (Две и более секущих плоскостей) | | | | | 1.Полные 2. Местные 3. Половинчатые 1.Плоские 2.Развертываемые Полные разрезы могут быть продольными и поперечными. Плоские разрезы могут быть наклонными и ступенчатыми. 25. Местный разрез. Пример оформления. Местный разрез служит для выяснения внутреннего устройства детали лишь в отдельном месте. Делается только со стороны вида. Отделяется от вида сплошной основной волнистой линией.  26. Ломаный разрез. Пример обозначения и оформления разреза. Одну секущую плоскость оставляем на месте, а вторую поворачиваем до совмещения с первой плоскостью. Элементы детали расположенные за секущей плоскостью, не перемещают. Место соединения плоскостей обозначают разомкнутой линией.  27. Ступенчатый разрез. Пример обозначения и оформления разреза. Секущие плоскости расположены параллельно друг другу и выявляют внутреннее устройство детали на своем участке. Сечения, полученные от разных плоскостей, совмещают в одну плоскость чертежа. Границу сечения не показывают. 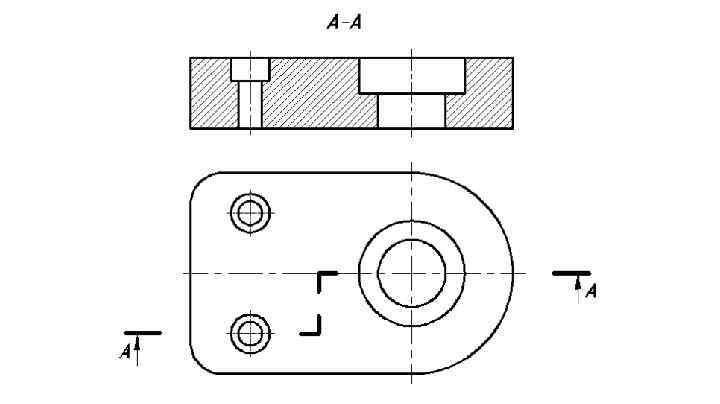 28. Простые разрезы. Половинчатые и полные разрезы Простые разрезы – при одной секущей плоскости Такие разрезы располагают на месте видов (главный, сверху, слева) Выполнение разреза на одном и том же виде не влечёт изменения других видов Продольные разрезы – две секущие плоскости направлены вдоль длины или высоты предмета  Поперечные разрезы – секущие плоскости направлены перпендикулярно длине или высоте предмета. Обозначается разрез аналогично сечению (с двух сторон) Если секущая плоскость совпадает с плоскостью симметрии детали в целом и находится непосредственно в проекционной связи, между двумя изображениями нет третьих изображений, то данный разрез не обозначается. Если деталь симметричная, то на одном изображении можно соединить половину вида и половину разреза 29. Условности ГОСТ 2.305-68, применяемые при построении разрезов. 1) Допускается изображать не все, что расположено за секущей плоскостью, если это не требуется для понимания конструкции предмета.  2) В случаях подобных указанному ну рисунке, стрелки, указывающие направление взгляда, наносят на одной линии.  3) Когда секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими-либо другими изображениями, для горизонтальных, фронтальных и профильных разрезов не отмечают положение секущей плоскости и разрез надписью не сопровождают (например, разрез на месте главного вида).  4) Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистой линией или сплошной тонкой линией с изломом .  5) Если при этом соединяются половина вида и половина разреза, каждый из которых является симметричной фигурой, то разделяющей линией служит ось симметрии. 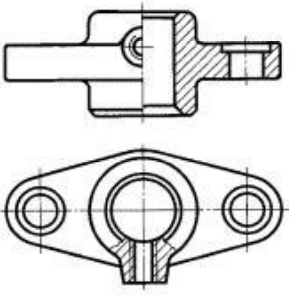 6) Допускается также разделение разреза и вида штрихпунктирной тонкой линией, совпадающей со следом плоскости симметрии не всего предмета, а лишь его части, если она представляет собой тело вращения. 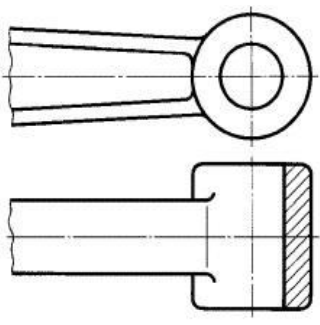 7) Если проекция ребра предмета совпадает с осевой линией, то при выполнении неполного разреза для показа наружного ребра разрез частично уменьшается . 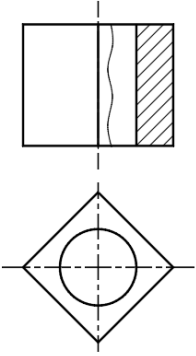 8) Для показа внутреннего ребра разрез увеличивается. 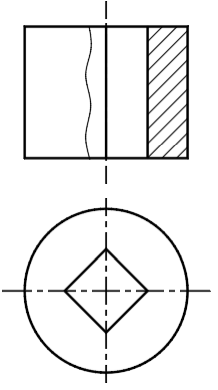 9) Для показа наружного и внутреннего ребра разрез частично уменьшается и частично увеличивается. 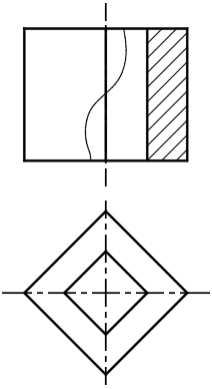 10) Отверстия на круглых фланцах или равномерно расположенные по окружности выкатываются в плоскость разреза, но не под элемент детали (типа ребра жесткости). 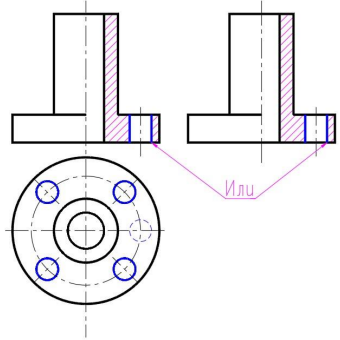 1 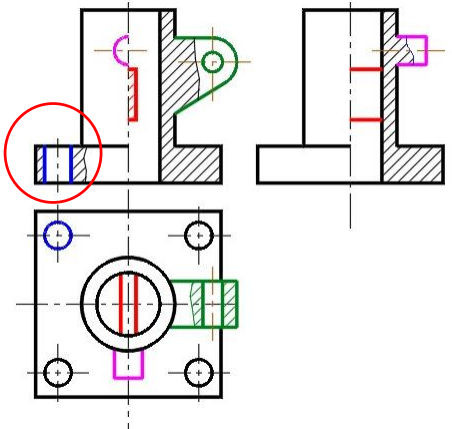 1) Отверстия на прямоугольных фланцах и не попадающие в секущую плоскость показываются местным разрезом со стороны вида и отделяются от вида сплошной волнистой линией. 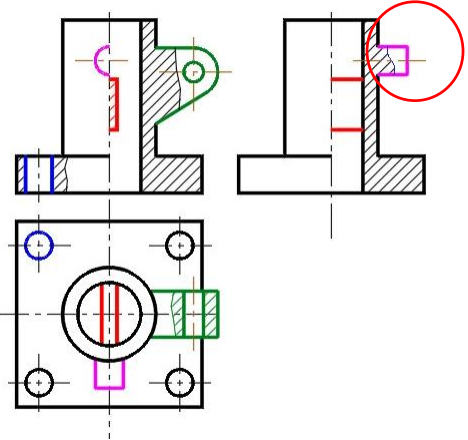1  2) Если секущая плоскость проходит вдоль оси монолитного выступа, то заштриховывается часть выступа. Другая часть отделяется сплошной волнистой линией от разреза. 13) Если секущая плоскость проходит вдоль оси проушины, то заштриховывается часть проушины. Остальная часть отделяется сплошной волнистой линией от разреза. Отверстие в проушине показывается местным разрезом. 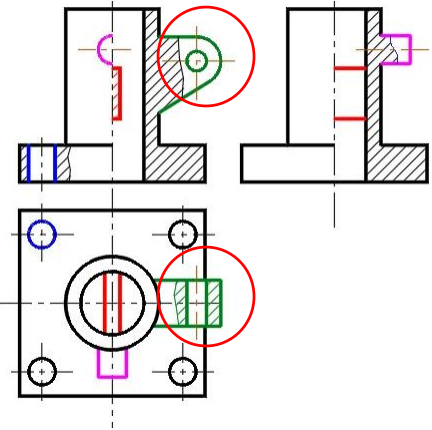 14) Если секущая плоскость направлена вдоль оси или длинной стороны тонкой стенки, типа ребра жесткости, то стенку и ребро жесткости не заштриховывают в разрезе и отделяют от остальной части детали сплошной основной линией. В поперечном же разрезе - штрихуют. 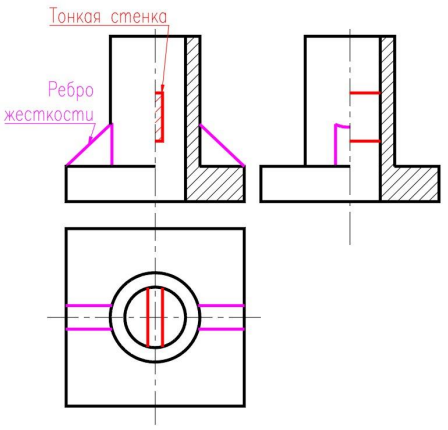 30. Классификация размеров детали. Понятие базы. Примеры. Классификация размеров: Габаритные (определяют внешние размеры детали) 2. Размеры - формы (определяют форму отдельных элементов детали) 3. Размеры взаимного расположения этих форм (размеры расположения) 4. Справочные размеры (не используются при изготовлении детали но облегчают чтение чертежа) обозначение: * - размер для справок (над основной надписью - технические требования) Размерная база - какая-либо поверхность, линия или точка детали, по отношению к которой рассматривают положение одного элемента детали относительно другого. Конструкторская база – база, используемая для определения положения детали или сборочной единицы в изделии. Они подразделяются на основные и вспомогательные. Основная база – конструкторская база детали или сборочной единицы, используемая для определения их положения в изделии. Вспомогательная база – конструкторская база детали или сборочной единицы, используемая для определения присоединяемого к ним изделия. 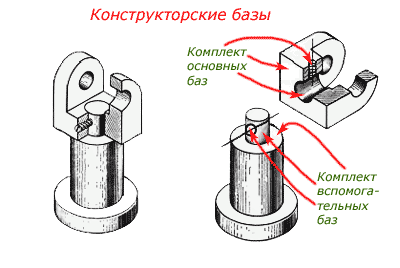 Технологические базы назначают при технологическом проектировании изготовления изделий и непосредственно в процессе их производства. Технологическая база – база, используемая для определения положения заготовки или изделия при изготовлении и ремонте. 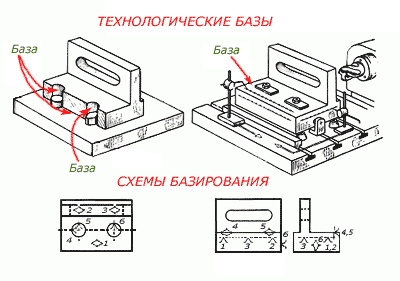 При контроле размеров, точности формы и расположения поверхностей выполняются измерения с использованием измерительных баз. Измерительная база – база, используемая для определения относительного положения заготовки или изделия и средств измерения. 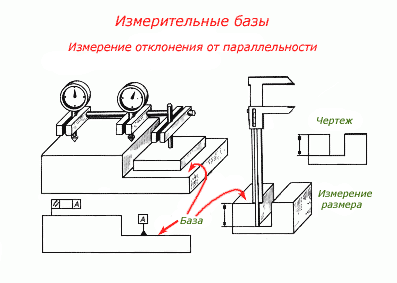 Способы нанесения размеров. 1)Координатный способ. 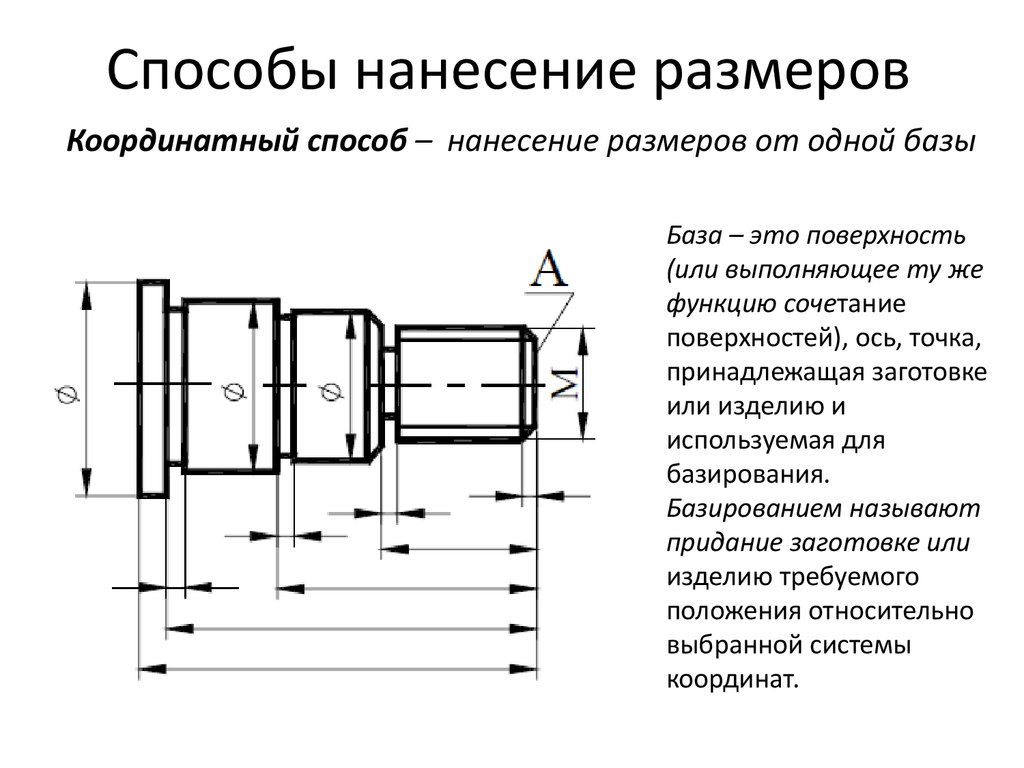 2)Цепной способ. 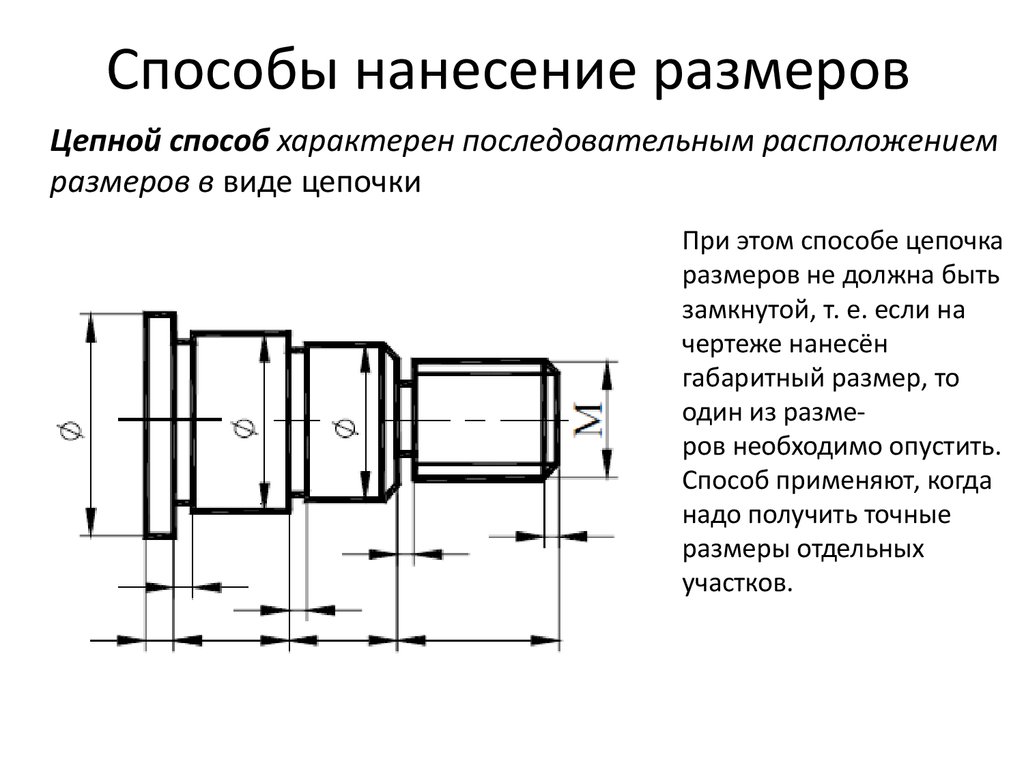 3)Комбинированный способ.  | ||||||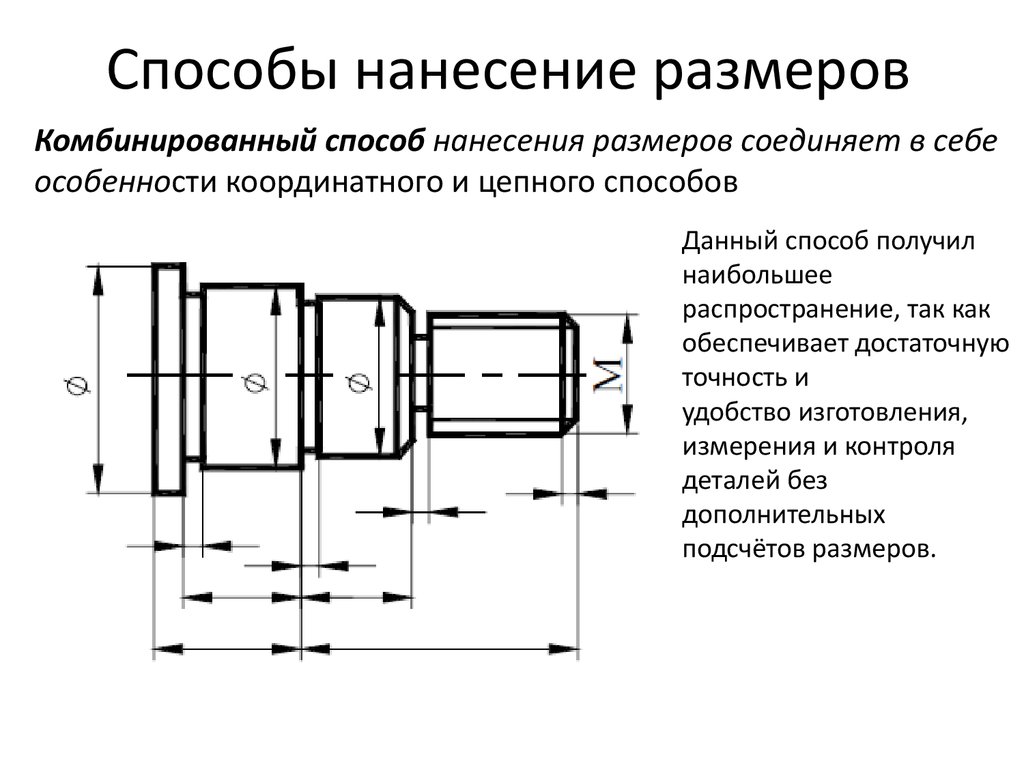
