Шпоры. 1. Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры
 Скачать 111.9 Kb. Скачать 111.9 Kb.
|
|
1.Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры. Множество—неопределяемое понятие, совокупность определенных объектов различных между собой, обозначается прописными(большими) буквами лат алфавита. Пример: множество целых чисел, действ чисел, студентов в группе, пар в аудит. Объекты состовляющие множество наз элементами этого множества и обознач строчными(маленькими) буквами лат алфавита. Пустое множ—это множ, которое не имеет элементов и обозначений. Способы задания множеств 1.перечисление элементов. Например: А={1,2,t,a}, бесконечное множество перечислению задать нельзя. 2.с помощью характеристического свойства. Выглядит так: {x|P(x)} (множество всех элементов xx, для которых высказывание P(x)P(x) истинно). 3.с помощью порождающей построения элементов(задание формулы). 4.с помощью графика. Множества А и В называются равными, если они состоят из одних и тех же эдементов. Например: А=В.;A={1,2,3,4}.;B={x|x ∈ Z∧x2<4}.;A=C;C={1,3,4,2}. Множество Х является подмножеством множества Y, если любой элемент множества Х ∈ (принадлежит/входит) и множеству Y. Обозначается X⊆Y. Пустое множ яв подмнож в любом другом множестве. Операции над множествами. Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В. 1.Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6} 2.Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4} 3.Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2} A\B 4.пусть все рассматриваемые множества яв подмнож в некотором множестве И в рамках некоторой теории. Оно наз универсальным множеством. В элементарной математике все числовые множества яв подмнож во множ действительных чисел. Дополнение к множ А наз множ И\А(И без А). Пример: А={-1,0,3,4}. B={0,4,6}.;А ∪ В={0,4,3,6,-1}.;А ∩ В={0,4}.;A\B={-1,3}.;B\A={6}. Круги эйлера 2. Отображения. Примеры. Область значений и область определения отображения. Инъективное, сюръективное и биективное отображение. Пусть X, Y — произвольные непустые множества. Определение. Отображение f из множества X во множество Y — это правило, при помощи которого каждому элементу x∈X ставится в соответствие однозначно определенный элемент y∈Y. Множество Х называется областью определения отображения f; множество Y — его областью значений. {\displaystyle D(f)} Если на множестве Х{\displaystyle X} задана функция, которая отображает множество Х {\displaystyle X} в другое множество, то множество Х {\displaystyle X} называется областью определения или областью задания функции. Более формально, если задана функция {\displaystyle f}f , которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: {\displaystyle f\colon X\to Y}f:X--Y то множество {\displaystyle X}X наз областью определения или областью заданияфункции {\displaystyle f} f и обозначается {\displaystyle D(f)}D(f). Отображение f из Х в Y называется инъективным, если для любых х1, х2∈Х из неравенства х1 ≠ х2 следует неравенство f(x1) ≠ f(x2). Отображение f из Х в Y называется суръективным, если множество значений f(X) совпадает с областью значений Y. Отображение f из Х в Y называется биективным, если оно суръективно и инъективно одновременно. 3. Матрицы: определение, размерность, примеры. Квадратная матрица, нулевая матрица, согласованные матрицы. Операции над матрицами: сумма и умножение. Матрица—это прямоугольная таблица с элементами из некоторого не пустого множества. Если матрица содержит m строк и n столбцов, то говорят. Что матрица имеет размерность mxn Квадратной матрицей наз матрица размерности nxn. Прямоугольной матрицей наз матрица если m не ровно n. Матрица содержащая 1 столбец-столбцовая матрица. Есть и матрица-строка. Нулевая матрица—это матрица, в которой все элементы =0. Единичная матрица—матрица, квадратная, в которой на гланой диагонали стоят 1-цы. А все остальные элементы—0. Матрицы Amxn и Bkxc наз согласованными, если n=k( количество столбцов матрицы А равно кол строк матрицы В Суммой матриц A и B одного размера называется матрица C=A+B такого же размера, получаемая из исходных путем сложения соответствующих элементов. Матрицы складываются поэлементно. Слаживать матрицы можно лишь одного размера. Произведением матрицы А*В определено только в том случае, если число столбцов матрицы а равно числу строк матрицы В Аmxk*Bkxn=C=A*Bmxn 4. Матрицы: определение, размерность, примеры. Определитель матрицы второго и третьего порядка. Свойства определителя. Матрица—это прямоугольная таблица с элементами из некоторого не пустого множества. Если матрица содержит m строк и n столбцов, то говорят. Что матрица имеет размерность mxn Квадратной матрицей наз матрица размерности nxn. Прямоугольной матрицей наз матрица если m не ровно n. Матрица содержащая 1 столбец-столбцовая матрица. Есть и матрица-строка. Нулевая матрица—это матрица, в которой все элементы =0. Единичная матрица—матрица, квадратная, в которой на гланой диагонали стоят 1-цы. А все остальные элементы—0. Матрицы Amxn и Bkxc наз согласованными, если n=k( количество столбцов матрицы А равно кол строк матрицы В Определителем числовой матрицы яв число. Только у квадратной матрицы. Обозначается detA Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом: Свойства определителя: 1.Если строку(столбец) в определителе матрицы усножить на некоторое число лямда, то и сам определитель умножится на лямда. 2.Если к строке9столбцу) определителя прибавить другую строку, то значения не изменятся 3. Определитель, имеющий две равные строки, равен 0. 5. Системы линейных алгебраических уравнений. Метод Гаусса. Метод Крамера. Примеры. Решить систему это значит найти такие числа а1, а2,а3.(альфа)…..аn, что при подстановке их вместо переменных x1…xn получится m верных числовых равенств. Способы решения систем линейных уравнений: 1.метод крамера. Его можно применить если 1. Число уравнений совпадает с кол переменных; 2.определитель матрицы коэффиц не равен 0. 1.метод гаусса.( можно решить любую систему линейных уравнений). В каждом уравнении начиная со 2-го поочередно исключ переменные. Т.е во втором избавляются от одной переменной. В третьем от трех и т. Д. с помощью чего: в системе можно 1 урав умножить на число и прибавить к другому. 6. Функция. Предел функции. Примеры. Свойства. Пусть f(x) ф-ция непрерывного аргумента. Число А наз пределом ф-ции y=f(x) при стремлении 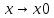 , если для каждого сколько угодно малого числа , если для каждого сколько угодно малого числа 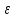 (эпсилон) найдется положительное число (эпсилон) найдется положительное число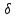 такое, что для всех Х, удовлетворяющих неравенству0< |x0-x|< такое, что для всех Х, удовлетворяющих неравенству0< |x0-x|<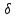 ( расстояние между х и х0 меньше б)будет следовать |A-f(x)|< ( расстояние между х и х0 меньше б)будет следовать |A-f(x)|<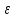 .( расст межд А и f(x) меньше Е) .( расст межд А и f(x) меньше Е)Lim(x 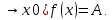 Литературное определение: Число А яв пределом ф-ции f(x), если можно обеспечить сколь угодно малое отличие f(x) от А при выборе достаточно близкого от х0 значения (х 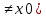 Пример: У= 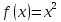 ; 1). lim ; 1). lim 2). Lim(x  3). Lim(x  Свойства: Пусть заданы ф-ции области определения которые совпадают p(f)=p(g), тогда limf(x)=A; limg(x)=B; (x  , тогда: , тогда:1). Предел суммы\разности 2 ф-ции равен сумм\разн их пределов: (f(x) 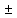 g(x))=A g(x))=A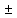 B; B;2). Предел произведения: lim(x 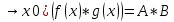 . .3).предел частного(деление): lim(x 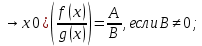 4).лимит любого числа это же число: lim(x 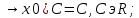 5). Константу можно выносить за знак предела: lim(x 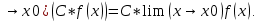 7. Функция. Предел функции. Непрерывность функции. Примеры. Пусть f(x) ф-ция непрерывного аргумента. Число А наз пределом ф-ции y=f(x) при стремлении 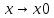 , если для каждого сколько угодно малого числа , если для каждого сколько угодно малого числа 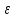 (эпсилон) найдется положительное число (эпсилон) найдется положительное число такое, что для всех Х, удовлетворяющих неравенству0< |x0-x|< такое, что для всех Х, удовлетворяющих неравенству0< |x0-x|< ( расстояние между х и х0 меньше б)будет следовать |A-f(x)|< ( расстояние между х и х0 меньше б)будет следовать |A-f(x)|< .( расст межд А и f(x) меньше Е) .( расст межд А и f(x) меньше Е)Lim(x  Литературное определение: Число А яв пределом ф-ции f(x), если можно обеспечить сколь угодно малое отличие f(x) от А при выборе достаточно близкого от х0 значения (х 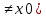 . .Ф-ция f(x) наз непрерывной в точке х=х0 э D(f), если придел при х 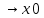 этой ф-ции равен f(x)=f(x0); lim(x этой ф-ции равен f(x)=f(x0); lim(x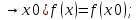 Пример: У= 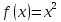 ; 1). lim ; 1). lim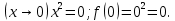 -ф-ция непрерывна в точке 0; -ф-ция непрерывна в точке 0;2). Lim(x 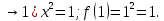 - в точке 1; - в точке 1;3). Lim(x 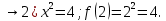 - в точке 2; - в точке 2;4).f(x) 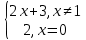 не яв непрерывной не яв непрерывнойВсе элементарные( школьные: квадр, линейн, логарифмич) ф-ции яв непрерывными в своей области определения 8. Производная функции одной переменной. Примеры. Основные правила дифференцирования. Производной ф-цией f(x) точки Х0 наз lim(предел(х 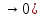 )= )=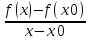 . При условии, что он существует. Обозначение: y’=f’(x) . При условии, что он существует. Обозначение: y’=f’(x)Пример:F(x)=2x Lim(x 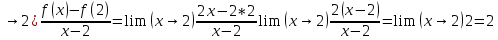 Лимит любого числа это же число. F’(2)=2 Пусть Х0—некоторое число Lim( 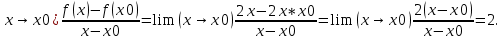 Значит для любого x0 f’(x)=2 Ф-ция f(x) наз дифференцируемой на промежутке Х, если в каждой точке промежутка Х сущ производная этой ф-ции. Операция нахождения производной наз дифференцированием. Основные правила: 1).производная от суммы\разности равна сумм\разн производных 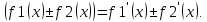 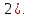 произведение производных произведение производных(f1(x)*f2(x))’=f1’(x)*f2(x)+f2’(x)*f1(x). 3). Произв частного 2-х ф-ций 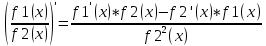 . .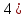 . Постоянный множительно можн выносить за знакпроизводной . Постоянный множительно можн выносить за знакпроизводной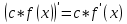 |
