Шпоры. 1. Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры
 Скачать 111.9 Kb. Скачать 111.9 Kb.
|
|
Здесь 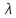 —среднее число событий А, появляющихся за еденицу времени. —среднее число событий А, появляющихся за еденицу времени.Для задания этого закона требуется только один параметр— 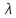 . .Мх=Dх= λ Бх= 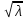 . .Пример: Пусть в середине раб дня среднее число запросов= 2 за секунду. Какова вер того, что за секунду не поступит не одного запроса, и что за 2 сек—10 запросов. Поскольку правомерность закона Пуассона не вызыв сомн и его параметр задан (λ=2), то решение сводится просто к применению формулы: 1). T=1, M=0; Mx= λ=2 Р(х=0)= 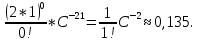 2). t=2, M=10 P(x=10)= 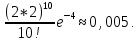 33. Равномерный закон распределения. Применение. Математическое ожидание, дисперсия и среднеквадратичное отклонение. Пример. Пусть Х—непрерывная СВ, все значения, которые находятся на отрезке[a,b] она может принимать с одинаковой вероятностью. Тогда говорят, что СВ Х распределена по равномерному закону. СВ Х распределена на отрезке [a,b] равномерно, если: f(x)= 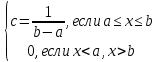 ;Mx= ;Mx=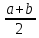 ; Dx= ; Dx=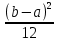 ;Бx= ;Бx=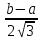 Пример: Минутная стрелка часов делает скачок на следующее деление, когда реальное время превышает указанное значение на 0,5 минуты. При взгляде на часы фиксируется время. Какова средняя ошибка в показаниях часов и каков разброс ошибки? Х—ошибка мин стрелки. Х принадлежит[-0,5;0,5]; Мх(средняя ошибка)= 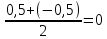 .( это очнач что сист ошибки нет, она накапливается). .( это очнач что сист ошибки нет, она накапливается).Бx= 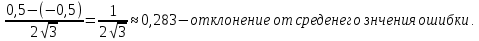 34. Нормальные закон распределения. Применение. Математическое ожидание, дисперсия и среднеквадратичное отклонение. Правило трех сигм. Пример. Один из само часто используемых Нормальный закон распределения. Непрерывная СВ распределена по нормальному закону, если её плотность вероятности записывается след образом:f(x)= 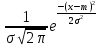 CВ, распределенная по нормальному закону с параметрами m u 𝜎 обознач след образом N(m, 𝜎) Если m=0, a 𝜎=1, то получим стандартное нормальное распределение N(0,1) f(x)= 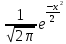 ,а функция распределения будет иметь вид F0(x)= ,а функция распределения будет иметь вид F0(x)= 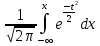 F0(x)=φ(x)=-0,5 φ(x)-интегральная функция Лапласа. Замечание: знач функции Лапласа приведены в таблице для положит знач х, так же φ(-х)=-φ(х)) Если СВ распределена по нормальному закону спараметрами m и λ, то вероятность того, что х находится между 𝛼 и 𝛽=P(𝛼<𝑥<𝛽)=𝜑( 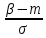 )−𝜑( )−𝜑(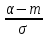 ) )P(x< 𝛽)=𝜑( 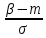 )+0,5 )+0,5P(x>𝛼)=0,5−𝜑( 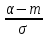 ) )Применение, например, погрешности измерений, погрешности при стрельбе, некоторые характеристики живых организмов и популяций и др. Математич ожидание дискретной СВ наз. сумма произведений всех знач. СВ на соответствующей им вероятности. Обознач М(х), МХ М(Х)=Х1Р1+Х2Р2+…+ХnРn Таким образом мат ожидание-это сред знач СВ, либо центр группирования знач СВ. Дисперсия характеризует разбросанность значений СВ (рассеивание около её математич ожидания) Дисперсия СВ это математич ожидание квадрата отклонений СВ от её математич ожидания D(X)=DX=M((X-M(X))2) x-дискретная СВ Х1 Х2 Х3 … хn Р1 Р2 Р3 … рn D(x)=(x1-M(x))2p1+(x2-M(x))2p2+…+(xn-M(x))2pn ,если Х-непрерывная СВ, f(х)- её плотность распред . D(x)=∫((𝑥−𝑀(𝑥))2−𝑓(𝑥)𝑑𝑥+∞−∞,если х принимает знач на всём -∞ числовом промежутке D(x)=∫(𝑥𝑏𝑎-M(x))2f(x)dx, x€[a,b] Недостаток дисперсии-это её размерность, она не совпадает с размерностью СВ в отличие от мат ожидания. Её размерность это квадрат размерности СВ (если СВ измеряется, например, в рублях, то дисперсия будет измеряться в руб 2). На практике это неудобно, т.к. мы не можем узнать величину разброса. С этой целью выводится ещё одна хар-ка СВ. Сред квадратичное отклонение – это числовая характеристика СВ, имеющая вид 𝛿(𝑥)=√𝐷(𝑥) Правило 3-х сигм (для нормального зак. Распред.) С вероятностью более 0,997 случ.велична распределённая по нормальному закому будет принимать значения из промежутка (m-3 𝛿, m+3 𝛿), где m- матем. промежуток, а 𝛿 – сред неквадратичное отклонение. 35.Лингвистическая переменная. Нечеткие множества: определение, примеры, формы записи. Функция принадлежности. Точка перехода. Примеры стандартных форм функций принадлежности. Лингвистической переменной наз переменная, значение которой явл слова или предложения естественного языка. (Прим. Возраст-это лингвистич переменная, если её значения не числа, а слова (молодой, немолодой, старый) Лингвистич знач х переменной u характеризуется функцией совместимости, которая ставит каждому знач u число в промежутке [0,1](число означ степень совместимости) Универсальное множество- это множество, которое содержит все рассматриваемые множества, и соответственно элементы этих множеств. Нечетким множеством А, универсального множества U, наз множества пар, состоящих из элементов множества U, и соответствующим им степеней принадлежности 𝜇А(х) 𝜇А(х)-это функция принадлежности, которая каждому элементу множества U ставит соответствие число𝜇А(u) 𝜖 [0;1] (это степень принадлежности элемента и множества А). Причем если 1) 𝜇А(u)=1, то u𝜖𝐴; 2) 𝜇А(u)=0, то u∉A; 3)0< 𝜇А(u)<1, то он частично принадлежит А. Если 𝜇А принимает значения только 0 и 1, то получим обычное классическое множество Нечеткое множество явл расширен. классич понятием множества Точка перехода нечеткого множества А наз. такой элемент универсального множества и степень принадлежности равна 0,5. Стандартные формы функции принадлежности: 1) Функция принадлежности класса S S(x,a,b,c)= 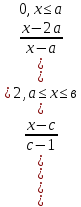 (пример, Пусть u=[0;100000p] А-большие деньги а=100р b=10000р с=10100/2=5050р.) 2) Функция класса 𝑙 𝑙 (x,a,b)= 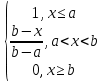 (Пример. Множество А-низкая скорость авто на трасе с мин скоростью 50 км/ч.U=[0,300] а=50км/ч b=150 км/ч) 3) Функция класса t t(x,a,b,c)= 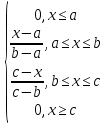 (Прим. Пусть А-это температура , комфортная для плавания в средиземнм море U=[140,350]Функцию распред можно составить на основе опытов, т.е. организовать опрос купающихся по степени комфортности температуры и вывести сред знач.) |
