Шпоры. 1. Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры
 Скачать 111.9 Kb. Скачать 111.9 Kb.
|
|
9. Производная функции одной переменной. Производная второго порядка. Производная сложной функции. Производной ф-цией f(x) точки Х0 наз lim(предел(х 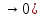 )= )=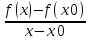 . При условии, что он существует. Обозначение: y’=f’(x) . При условии, что он существует. Обозначение: y’=f’(x)Пример:F(x)=2x Lim(x 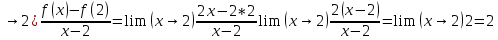 Лимит любого числа это же число. F’(2)=2 Пусть ф-ция f(x) имеет производную в каждой своей области определения, ели ф-ция f’(x) имеет производную в точке х0 э D(f),то она наз производной второго порядка. F’’(x)=(f’(x))’ Пример: 1). F(x)= sinx; f’x=cosx; f’’(x)=-sinx 2). F(x)= 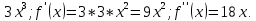 3). F(x)=2x-5; f’(x)=(2x-5)’-(2x)’-(5)’=2(x)’-0=2; f’’(x)=(2)’=0 Производная сложной ф-ции: 1).Ф-ция u= 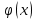 имеет производную точки х0: Ux’= имеет производную точки х0: Ux’=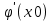 . .2).ф-ция y=f(u) имеет производную точку u0=y(x0) выглядит так: y’u=f’(x0). Тогда ф-ция y=f(y(x)) имеет производную в точке х0; y’=f’(u0)* 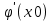 . .[y’x=y’x*u*x]—производная сложной ф-ции. Пример: 1).Y=sin(3x); u=3x; y=sin u; y’=sin’(u)u’=cos u*(3x’)=cos(3x)*3=3cos 3x 2).y= 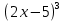 (u); y’= (u); y’=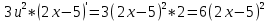 . .10. Исследование функции и построение графика. Промежутки возрастания и убывания. Экстремумы. Необходимое условие экстремума. Примеры Пусть для ф-ции f(x) D(f)=A и f(x) имеет производную в каждой точке А и непрерывна на А. Тогда: 1.если f’(x)>0, тогда для любого х из множества А , то f(x) монотонно возрастает (x1>x2, то f(x1)>f(x2)) 2.если f’(x)<0 , тогда для любого элемента х их множества А, то f(x) монотонно убывает (x1>x2,то f(x1)< f(x2)) Пример: у=3х; y’=3>0=>y 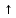 (На чертеже через 1) (На чертеже через 1)Если f’(x)принимает значение 0 в конечном числе точек промежутка А, то предыдущая теорема так же имеет силу. Пример: y= 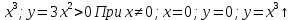 (на чертеже через 0) (на чертеже через 0)Определение возрастающей функции. Функция y=f(x) возрастает на интервале X, если для любых x1 э X и x2 э X, x2>x1 выполняется неравенство f(x2)>f(x1) . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y=f(x) убывает на интервале X, если для любых x1 э X и x2 э X, x2>x1 выполняется неравенство f(x2)<f(x1) . Другими словами – большему значению аргумента соответствует меньшее значение функции. Точку x0 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство f(x0) 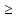 f(x). Значение функции в точке максимума называют максимумом функции и обозначают Ymax. f(x). Значение функции в точке максимума называют максимумом функции и обозначают Ymax.Точку x0 называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство f(x0) 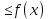 . Значение функции в точке минимума называют минимумом функции и обозначают Ymin. . Значение функции в точке минимума называют минимумом функции и обозначают Ymin.Под окрестностью точки x0 понимают интервал(x0- 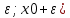 , где , где 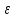 - достаточно малое положительное число. - достаточно малое положительное число.Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции. Все возсожные экстремумы ф-ции на отрезке это точки в котрых производная=0 либоих не сущ( но это не значит, что все эти точки яв экстремумами). Правило нахождения экстремумов Пусть Х1,…Хn это точки в котрых производная +0 либо не сущ ----а----Х1-------------Хn------в Рассматриваем каждый промежуток по отдельности: (а.х1); (х1,Хn); (Хn,в). На каждом их этих промежутков производная =0 либо не сущ. Сама ф-ция либо возрастает либо убывает. Если, например, на промежутке(а,Х1) f’(x)>0, то Х1-это точка максимума; (Х1,Х2) f’(x)<0, то это точка минимума. 11. Исследование функции и построение графика. Вогнутость и выпуклость. Точки перегиба. Примеры. Пусть для ф-ции f(x) D(f)=A и f(x) имеет производную в каждой точке А и непрерывна на А. Тогда: 1.если f’(x)>0, тогда для любого х из множества А , то f(x) монотонно возрастает (x1>x2, то f(x1)>f(x2)) 2.если f’(x)<0 , тогда для любого элемента х их множества А, то f(x) монотонно убывает (x1>x2,то f(x1)< f(x2)) Пример: у=3х; y’=3>0=>y 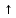 (На чертеже через 1) (На чертеже через 1)Если f’(x)принимает значение 0 в конечном числе точек промежутка А, то предыдущая теорема так же имеет силу. Пример: y= 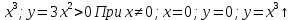 (на чертеже через 0) (на чертеже через 0)Ф-ция на промежутке наз выпуклой, если она не выше касательной в любой точке этого промежутка. Ф-ция наз вогнутой, если она не ниже любой касательной на этом промежутке. Точка, в которой ф-ция меняет вогнутость на выпуклость либо наоборот наз точка перегиба Правило нахождения точки перегиба: если Х- точка перегиба, то f’’(x) либо =0 либо не сущ. Т.е. для нахождения точки перегиба нужно найти 2-ю производную ф-цию. Если на промежутке f’’(x)>0,тоф-ция вогнутая, если <0, то выпуклая; в этом случае х1- точка перегиба. Анологично, если на промеж от(а до х1)- выпукл, а (х1,х2)-выгн, то х1- точка перегиба ( если при переходе через Х f меняет знак, то х- точка перегиба) 12. Первообразная функция функции одной переменной. Неопределенный интеграл. Таблица основных интегралов. Основные свойства неопределенного интеграла. Примеры. Ф-ция F(x) наз. Первообразной функции f(x) на промежутке Х, если на этом промежутке производная =некотрой ф-ции f(x) т.е (F(x))’=f(x). Значит f(x) яв производной (F(x))’. Совокупность всех первообразных для f(x) наз. Неопределенным интегралом ф-ции f(x) от переменной х, обозначается 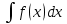 =F(x)+C =F(x)+CВ этом случае f(x) наз—подинтегральной ф-цией.  Основные свойства интегрирования 1.Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла 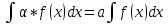 2.3 Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций 13. Определенный интеграл. Геометрический смысл определенного интеграла. Рассмотрим непрерыв. ф-цию у=f(х) на промежутке [a,b], которая на этом промежутке принимает положительное значение, и рассмотрим фигуру ограниченную графиком ф-ции у=f(х), х=а, х=в, у=0. С помощью определенных интегралов можно почтитать площадь криволинейной трапеции. Х1,Х2,…,Хn=b;a=X0;X=X0 В результате мы развили криволинейную трапецию на N криволиненых трапеций, тогда если их площадь обозначить через S1,S2,…,Sn. Тогда плозать нашей трапеции=S=S1+S2+…+Sn На промежутке от [x0,X1] выберем з1(дзета) на этом отрезке, на отрезке от [X1,X2]-з2, на [Xn-1,Xn]-зn. В этом случае площадь S1=площади треугольникасо сторонами(х1-Х0) и f(з(дзета)1) Т.е S1 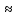 f(з1)*(Х1-Х0)= f(з1)* f(з1)*(Х1-Х0)= f(з1)*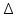 Х1. Анологично S2=f(з2)* Х1. Анологично S2=f(з2)*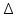 Х2…. (По i од 1 до n) Х2…. (По i од 1 до n)Тогда вся площадь S= 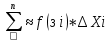 F(з1) 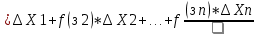 = =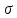 При стремлении 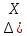 ) )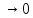 все криволинейные трапеции будут приближаться к прямоугольникам. А площадь будет приблиз к площ прямоуг. все криволинейные трапеции будут приближаться к прямоугольникам. А площадь будет приблиз к площ прямоуг.Обозначение предела—I= 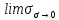 . .Определенный интеграл Конечный предел I= 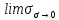 . Наз определенным интеграломф-ции f(x), в промежутке[a,b]и обозначается I= . Наз определенным интеграломф-ции f(x), в промежутке[a,b]и обозначается I=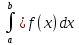 , а-нижний предел, в-вершний предел интеграла. , а-нижний предел, в-вершний предел интеграла.Если такой предел сущ, то ф-ция f(x) наз интегрируемой на промежутке [a,b]. Этот опред интеграл= площадикриволит трапеции, ограниченной графиком f(x). Определенный интеграл сущ не всегда, следовательно площадь можно высчитать не всегда, но для элементарных (непрерывных) можно. Г.с.:Определённый интеграл 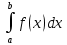 {\displaystyle \int \limits _{a}^{b}f(x)\,dx} численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a{\displaystyle x=a} и x=b {\displaystyle x=b} и графиком функции f(x) {\displaystyle f(x)}. {\displaystyle \int \limits _{a}^{b}f(x)\,dx} численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a{\displaystyle x=a} и x=b {\displaystyle x=b} и графиком функции f(x) {\displaystyle f(x)}.14. Определенный интеграл. Свойства, примеры. Формула Ньютона-Лейбница. Вычисление площади фигур с помощью определенного интеграла. Если независимо от способа разбиения отрезка [a,b] на части, для ф-ции f(x) существует конечный предел, то этот предел наз Определенным интегралом. Свойства определенной интеграла: 1). По определению 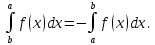 2). Аддитивность. Если ф-ция f(x) интегрируема на отрезках [a,c] и [c,b], a<c<b,то она интегрируема и на отрезке [a,b]: 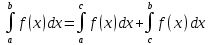 . .3).Постоянный множитель можно выносить за знак интеграла 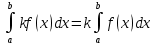 4). Определенный интеграл от алгебраической суммы нескольких ф-ций равен алгеб сумме интегралов от слагаемых: 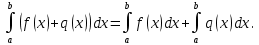 Формула Ньютона-Лейбница Если f(x)интегрируемая ф-ция на отрезке [a,b],то интеграл высчитывается след образом 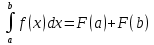 . Где F(x)- некоторое произвольное прообразное для f(x) ф-ции. . Где F(x)- некоторое произвольное прообразное для f(x) ф-ции.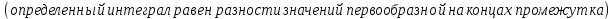 Пример: вычислить: 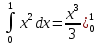 = =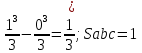 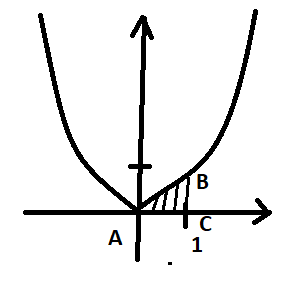 Если f(x) принимет на промежутке [a,b] только отрицательные значения, то S фигуры ограниченной этойфигурой(кривой) осью Ох и прямыми х=а, х=в, то S этой фигуры= 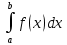 . .Пример: Найти Sфигуры, грани эой прямой с прямыми х=-1, х=-2, у=0,у=2х
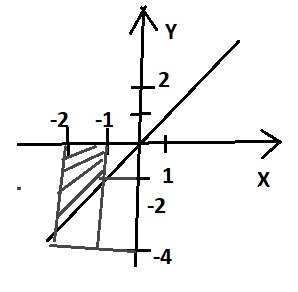 |
