Шпоры. 1. Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры
 Скачать 111.9 Kb. Скачать 111.9 Kb.
|
|
S=- 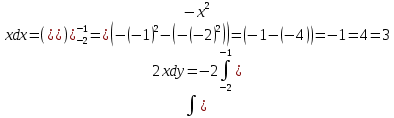 Теор: пусть заданы 2ф-ци y=f1(x), y=f2(x)и на промеж [a,b] f1(x) находится выше, чем f2(x) (на чертеже чертится выше. Оси не имеют значения). Тогда S фигурв огранич этими 2ф-циями и прямими х=а, х=в; = 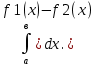 15. Основы комбинаторики: перестановка, сочетания, размещения. Комбинаторные принципы сложения и умножения. Примеры. Перестановкой из n элементов наз упорядоченный набор этих элементов (расположение этих элементов в определенном порядке). Количество различных перестановок из nэлементов равно Pn=P(n)=n! [0!=1].(= 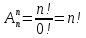 Пример:{1,2,3}—2,3,1—перестановка. В группе 6 чел. Сколько можно составить различных списков из этих 6 человек.6!=720. список-это перестановка Сочетанием из m элементов по k наз множ содержащее k различных элементов из числа m заданных.{1,2,3,4}. Сочетание из 4 по 4 по 2: {2,3}, {1,2}. В сочетании порядок не имеет значения. Кол-во всех сочетаний из m по k равно 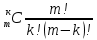 Пример: сколько можно составить подгрупп содержащих по 2 чел из группы из 6 чел 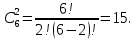 Размещением из m по k наз. Упорядоченный набор их к-элементов выбранных из имеющихся м-элементов. (то же самое, что и сочетание, но порядок имеет значение). Кол-во всех возможных размещений из m по k 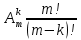 Пример:в группе 6 чел, сколько пожно составить подгрупп состоящих из 2 чел. 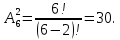 Правило суммы: если некоторый объект А можно выбрать mспособами, а объект В можно выб k способами, то выбрать выбрать А либо В можно m+k способами. Пример: из уникак до дома можно добраться с 2 остановок, с 1-ой идут 2 тралика, со 2-ой- 2 и 1 тралик. Сколько сущ способов добраться домой. С 1-ой= 2 варианта; со 2-ой=3 вар; 2+3=5 способов. Правило произведения: Если объест А можно выб m способами и после каждого такого выбора объект В можно выб k способами, то пару(А,В) можно выб m*kспособами Пример: из Минска в Б ведут 7 дорог, из Б в А—11 дорог. Ск сущ способов поехать из М в А через Б; 7*11=77 16. Случайное, достоверное, невозможное событие. Совместные и несовместные события. Вероятность случайного события. Классическая формула вычисления вероятности. Примеры. События это любой факт ,который может произойти или не произойти в результате опыта, обознач соб. Больш букв лат алф Достоверным соб наз соб, которое при определенном комплексе условий обязательно произойдет. Невозможным соб наз соб, которое при определенном комплексе условий точно не произойдет. Случайное соб наз соб, которое может произойти, а может и не произойти. 2 события наз несовместными(зависимыми), если появление одного влияет на появление другого. 2 соб наз совместными(независимыми), если появление одного не влияет на появ другого. Любое событие, котрое в рез опыта может произойти наз элементарным исходом. Каждому событию можно поставить соответствие на одно из чисел отрезка от 0 до 1, которое буд наз Классическая вероятность: Пусть n—это число равно возможных исходов, m—это число исходов, состовляющих событие( их часто наз благоприятные исходы) . тогда вероятность события А = (P(A)= 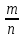 ). ).Например: бросается игральный кубик. 1)какова вер того, что выпадет 6; 2) какова вер того, что выпадет четное число. 1.n=6. Р(А)=1\6; 2.n=3. Р(А)=3\6=1\2. Класс вер предпологает конечное число исходов, m и n должны быть конечными числами. 17. Случайное, достоверное, невозможное событие. Совместные и несовместные события. Вероятность случайного события. Геометрическая вероятность. Примеры. Достоверным соб наз соб, которое при определенном комплексе условий обязательно произойдет. Невозможным соб наз соб, которое при определенном комплексе условий точно не произойдет. Случайное соб наз соб, которое может произойти, а может и не произойти. 2 события наз несовместными(зависимыми), если появление одного влияет на появление другого. 2 соб наз совместными(независимыми), если появление одного не влияет на появ другого. Геометрическая вероятность: применяется когда число исходов беспонечно. P(A)= 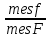 Пример: Анна потеряла ключи между 3 и 15 км , какова вер того. Что она их потеряла между 5 и 10 км А—«это потеряла ключи между 5 и 10 км»(событие) Mes F+ 15-3=12 (длина).;Mes f= 10-5=5( область, которая нас устраивает).;Р(А)=5\12. 18. Случайное, достоверное, невозможное событие. Совместные и несовместные события. Вероятность случайного события. Статистическая вероятность. Примеры. Достоверным соб наз соб, которое при определенном комплексе условий обязательно произойдет. Невозможным соб наз соб, которое при определенном комплексе условий точно не произойдет. Случайное соб наз соб, которое может произойти, а может и не произойти. 2 события наз несовместными, если появление одного исключ появление другого.( одновременно идет экзамен и фильм) 2 соб наз совместными, если появление одного не исключ появ другого. (2 стрелка) Статистическая вероятнось: Пусть А—случ событие. Проведем эксперимент n раз и посчитаем сколько раз произошло событие А. когда число m делить на n –m\n наз относительной частотой появления события А, если при достаточно больших значениях n это число группируется около некоторой остоянной( то постоянная—это число), то вер наступ соб Абудет примерно равна этому числу. И оно будет наз статичтической вер соб А. где m – число появления события, n – общее число испытаний. Р(А)= 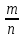 . .Пример: если подбросить идеальную монетку n раз и посчитать сколько раз выпадет орел, то при достаточно большом значении n 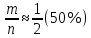 19. Действия над событиями: сумма, разность, произведение. Противоположное событие, его вероятность. Вероятность суммы совместных и несовместных событий. Примеры. Суммой(объединением) событий Аи В наз событие состоящеев появлении хотя бы одного из этих событий( А+В, А ∪ В). Произведением(пересечением) соб А иВ наз соб состоящее в появлении обоих событий(и А и В).( А*В. А ∩ В). Разностью соб А и В наз соб состоящие в появ соб А и не появлении соб В. (А-В. А\В). Пример: А—сегодня пойдет дождь В—сег пойд снег. А+В—«либо дождь либо снег»;А*В—«и дождь и снег».;А-В—«дождь, без снега». Противоположным событием А наз. Соб А(не А) состоящее в том, что соб а не наступило. Свойства: 1. Р(не А)=1-Р(А).( вер наст соб НеА= 1 –вер соб А) Пример: брос игр кубик. Найти вер того. Что выпадет не 3 А-« вер того, что выпадет не 3» Р(А)=1\6; Р(А)=1-1\6=5\6. 2. вер сумы 2 соб= Р(А+В)=Р(А)+Р(В)-Р(АВ). В следствие, если события А и В несовместны, то Р(АВ)=0( вер того, что произойдет и 1 и 2) Р(А+В)=Р(А)+Р(В). Пример: брос игра куб. какова вер, что вып 2 или 3. А—«выпадет2»; В—«выпадет 3»; Р(А)=1\6; Р(В)=1\6; Р(А+В)=1\6+1\6=2\6=1\3. 3. Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(ВС)-Р(АС)+Р(АВС), 4. Если событие А1,А2,……Аn образуют полную группу несовместных событий, то Р(А1) +Р(А2)+….Р(An)=1. 20. Произведение событий. Зависимые и независимые события. Условная вероятность. Вероятность произведения зависимых и независимых событий. Примеры. Произведением(пересечением) соб А и В наз соб состоящее в появлении обоих событий(и А и В).( А*В. А ∩ В). Соб А наз независимым от соб В, если вероятность соб Ане зависит от того, произошло или нет соб В. В противоположном случае оно наз зависимым от соб в. Вероятность, которая вычисляется при условии, что событие В произошло наз условной вер соб А. и обознач Р(А\В)( вер А при условии В). Вероятность произведения 2 соб = произведению вероятности 1 соб и вер 2-го соб, что 1 произошло: Р(А*В)=Р(А)*Р(В\А). Если А и В независимые соб, то Р(В\А) (совпадает)= Р(В). Тогда Р(АВ)=Р(А)*Р(В). Вероятность произведений произведения некоторых соб= произведению вер этих соб. Причем вер каждого последующего соб вычисляется при условии. Что все предыдущие произошли. Р(А2*А2*…*Аn)= Р(А1)*Р(А2\А1)* Р(А3\А2). Если все соб несовместны, то Р(А1*…*Аn)= Р(А1)* Р(А2)*…* Р(Аn). Пример: Есть 3 шара. 2 белых и 1 черн. 2 чел поочередно тянут по одному шару. Соб А—1 вытянул бел шар, соб в—2 вытянул бел шар. В зависит от А. Р(А)= 2\3 если А произошло, то Р(В)=1\2. 21. Гипотезы. Формула полной вероятности. Формула Байеса. Пример. Пусть событие А может произойти только вместе с одним из событий Н1, Н2…Нn., которые образуют полную группу несовместных событий. Тогда соб Н1, Н2…Нn наз гипотезом Формула полной вер: вер соб А=сумме произведений вер каждой гипотезы на вер соб А при условии этой гипотезы: Р(А)=Р(Н1) *Р(А\Н1)+Р(Н2)*Р(А\Н2)+…+Р(Нn)*Р(А\Нn). Применяется когда у события А есть сопутствующие условия и вероятность А меняется в зависимости от условий Пример: В эксперименте участвуют 10000 мужчин и 10 000 женщин, 5 % мужчин и 0,25% женщин страдают от дальтонизма, какова вероятность того, что наугад выбранный человек страдает дальтонизмом?. А- «человек стр. дальтон.». Н1-выбрали мужчину; Н2- выбрали женщину; Р(А)=Р(Н1) *Р(А\Н1)+Р(Н2)*Р(А\Н2)+…+ Р(н1)—вер того. Что быв муж( по класс вер)= 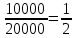 Р(Н2)—выб жен(класс)= 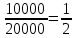 Р(А\Н1)- вер того. Что даль будет муж)=5%\100%=1\20. Р(А\Н2)-среди жен=0,25%\100%=25\10000=1\400. Р(А)=1\2*1\20+1\2*1\400=1\40+21\20=21\800=0,02620. Следсвие из теоремы полной вер яв теорема гипотеза (формкла Байеса). Пусть задано некоторое соб А и система гипотез Н1,Н2,…Нn для этого соб. В рез опыта произошло соб А. найти вер того, что соб А произошло при гипотезе Нi. Вычисляется по формуле Байеса Р(Hi\A)= 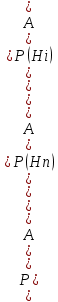 Пример: На экзамене 20 билетов. 5 лёгких и 5 сложных, 2 студента по очереди тянут билеты. Найти: 1) Вероятность того, что первый студент вытянет лёгкий билет 2) Второй студ. Вытянет лёгкий 3) второй вытянет лёгкий, какова вероятн. Того что первый также вытянет лёгкий. 22. Повторные независимые испытания. Формула Бернулли. Пример. Пусть некоторый опыт проводят n раз и каждый раз событие А может наступить с той же вероятностью Р(А) независимо от результатов предыдущих опытов. Это называется повторным независимым испытанием. Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом. Вероятность того, что событие А в n независимых повторных испыт произойдет k раз равно: Р(p,n,k)= 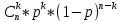 (ф-ла Бернулли) Р=р(А)- вероятн. Наст. События в одном испытании. (ф-ла Бернулли) Р=р(А)- вероятн. Наст. События в одном испытании.При больших значениях n формулой бернули пользоваться неудовно, так как n! Будет большим числов. В этих числав польз теоремой лапласа или формулой пуассона. Пример: Монету бросали 10 раз какова вероятность того, что герб выпадет 3 раза. Событие А-«выпадение герба в одном испытании», тогда р(А)=1/2. Р(1\2,10,3)= 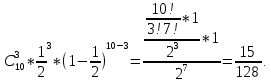 23. Повторные независимые испытания. Локальная теорема Лапласа. Пример. Пусть некоторый опыт проводят n раз и каждый раз событие А может наступить с той же вероятностью Р(А) независимо от результатов предыдущих опытов. Это называется повторным независимым испытанием. Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом. Теорема Лапласа N стремится к бесконечности(>50); Р(А) 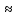 0,5 0,5Np(1-p)>10 Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы( не равна 0 или 1), то вероятность Pm,n того, что событие A появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции P(n,p,k) 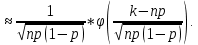 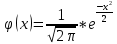 Значения ф-ции 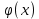 приведены в таблице для не отрицательных х, учитывая что ф(-х)=ф(х) приведены в таблице для не отрицательных х, учитывая что ф(-х)=ф(х)Пример: В семье 4 детей. Принимая равномерно рождение и мальч и дев найти вер того, что в семье: 1)3 мальч; 2)2 мальч; 3)не менее 3 мальч. Р=0,5; n=4 1). K=3. P(4;0,5;3)=p(3)= 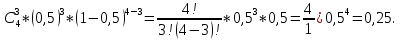 2). K=2; p(n,p,k)= 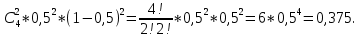 3).k 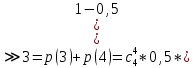 24. Повторные независимые испытания. Формула Пуассона. Пример. На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие A При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события A в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа m появлений события A в результате n испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события A в каждом испытании постоянна. Такие испытания называются повторными независимыми. Формула Пуассона Если вероятность p наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний n, но при небольшом значении произведения np получаемые по формуле Лапласа значения вероятностей Pm,n оказываются недостаточно точными и возникает потребность в другой приближенной формуле. Если вероятность p наступления события A в каждом испытании постоянна, но мала, число независимых испытаний n достаточно велико, но значение произведения np=λ остается небольшим (не больше десяти), то вероятность того, что в этих испытаниях событие A наступит m раз:т.е, если p->0 и λ= np 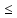 10, то P λ ,n 10, то P λ ,n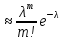 Пример: На заводе узготов 100 000 ваз. Вероятность того, что при перевозке ваза разовъется=0,0001. Найти вер того, что из 100 тыс ваз разобъется:1) 5 ваз; 2) манешь 4; 3) больше 2; Решение: n=100000; p=0,0001->0; λ= np=100000* 0,001=10  10 10Ф-ла: p(10,k)= 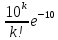 . .1).k=5, p(10;5)=0,0378 (по таблице) 2).k<4;p=p(10;0)+ p(10;1)+p(10;2) +p(10;3) 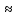 0,01 0,013).k>2;p=1-p(10;0)-p(10;1)-p(10;2)  0,997. 0,997.25. Случайные величины: дискретные и непрерывные. Закон распределения случайной величины. Закон распределения дискретной случайной величины: таблица и полигон распределения. Примеры. |
