Шпоры. 1. Множества. Способы задания множеств. Равные множества, подмножества. Операции над множествами. Примеры
 Скачать 111.9 Kb. Скачать 111.9 Kb.
|
|
Случ вел наз вел, которая в результате опытов может принимать одно и только одно определенное значение , до опыта неизвестное и зависящее от причин, которые нельзя учесть заранее. Примеры: выборыв представительские органы власти. Случайным событием является факт выбора(или невыбора);соц обследование. Случ соб- факт опроса того или иного человека. СВ обознач пропис буквами лат алфавита. А значение, которое она принимает строчными. Пример: бросается игр кубик, СВ Х—количество точек на выпавшей грани. Х:1,2,3,4,5,6 соответственно Х1=1, Х2=2, Х3=3, Х4=4, Х5=5,Х6=6. Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.( СВ наз дискретной, если все ее значения могут быть заранее перечислены). Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени, время выхода из строя работающего компьютера. Рассмотрим дискретную СВ Х. Пусть она может принимать значения Х1,х2,…,Хn. В результате опытов она принимает каждое их этих значенийс определенной вероятностью. Р(Х=Х1)=р1; р(х=х2)=р2;…….;Р(х=хn)=Pn. Законом распределения СВ наз соотношение определяющее связь между возможными СВ и соответствующими им вероятностями. Одной из форм задания закона распределения дискретной СВ яв таблица
графическое изображение закона распределения наз полигон. Пример: брос игр кубик, х- кол точек на грани.
Р1=1\6=р2=….. 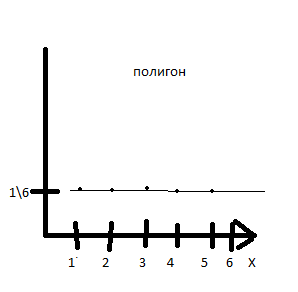 26. Непрерывные случайные величины. Функция распределения, ее свойства. Примеры. Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени. Ф-ция распределения СВ (интегральный закон распределения) наз вероятность выполнения неравернства Х<x1 F(x)=P(Х<x1). Ф-ция распределения определена не только для непрерывной СВ, но и для дискретной. Определение ф-ции распределения имеет наглядную геометрическую интерпретацию. Если рассматривать Х как случайную точку на числовой оси, то F(х) есть вероятность того, что случ точка попадет левее выбранной величины х. 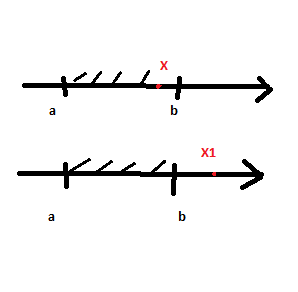 Свойства: вытекают из определения 1.F(x)—неотрицательная ф-ция, значения котрой заключены между 0 и 1. Т.е. 0 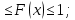 2.F( 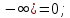 3.F( 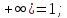 4.F(x)—неубывающая ф-ция своего аргумента. Т.е. если Х1>Х2, то F(X1) 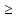 F(X2); F(X2);5.P(a 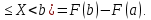 Пример: Время безотказной работы прибора имеет ф-цию распределения F( 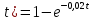 , t-время в часах. , t-время в часах.Какова вероятность, что прибор проработает не менее 30 и не более 40 часов? Х- безотказная работа прибора. Р(30 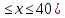 = F(40)-F(30)=(1- = F(40)-F(30)=(1-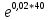 )-(1- )-(1-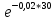 )= 1- )= 1-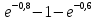 = =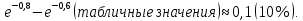 27. Непрерывные случайные величины. Плотность распределения, ее свойства. Примеры. Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени. Непрерывную СВ удовно описывать не только с помощью ф-ции распределения, но и с помощью ф-ции плотности распределения(дифференциальный закон распределения). Пусть х—непрерыв СВ, F(x)—ф-ция распределения этой величины . Если ф-ция х дифференцируема. Т.е. существует производная, то плотностью распределения СВ Х наз f(x)=F’(x) Таким образом Р(х1<x<x2)=F(x2)-F(x1)=F(x) 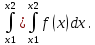 Геом смысл определенного интеграла—это площадь криволинейной трапецииограниченной: y=f(x); X=X1; X=X2; y=0; 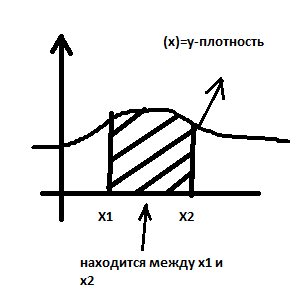 Если СВ принимает все свои значения на промежутке от А до В([a;b]), то р= 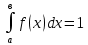 (Вер того, что она попадет 100%) (Вер того, что она попадет 100%)Плотность распределения сущ только для непрерыв СВ. Так как если х дискретная СВ, то ф-ция распределения будет не дифференцируема Свойства: 1.ф-ция плотности вероятности—неотрицательная ф-ция: f(x) 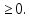 2.интеграл в бесконечных пределах от ф-ции плотности вероятности( если она задана на всей числовой оси) Пример: Найти плотность распределения и вероятность того, что прибор будет работать не менее 30 и не более 40 часов. Р(30 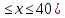 f(t)=F(t)=( 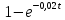 )= 0- )= 0-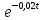 Р(30 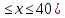 = = 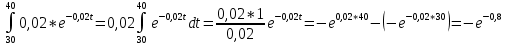 + +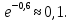 Пример. Пусть Х – СВ. плотность распределения: f(x)= 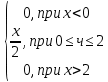 . .Найти P( 0 х 1 ),P( 0 х 2 ) P( 0 х 1 )= 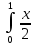 dx= dx=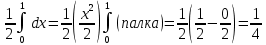 . .28. Математическое ожидание непрерывной и дискретной случайной величины, и его свойства. Примеры. Рассмотрим пример. Бросаются 3 игр кости и рассматривается СВ –сумма выпавших очков. Вполне очевидно, что выпадение 18 очков юудет в среднем происходить реже, чем 15 очков, и значительно реже, чем 12 очков. Если с некоторым весом усреднить все возмжные значения суммы выпавших очков( от 3 до 18), то получим величину, яв «центром» распределения возможных значений рассматриваемой СВ и наз ее мат ожид. Мат ожид СВ наз сумма произведений всех значений СВ на соответствующей им вероятности. М(х)=х1р1=х2р2+…+xnpn. Таким образом мат ожид это среднее значение СВ либо—центр группирования значений СВ. Пусть х—непрерывная СВ. если х принимает все свои значения на отрезке от а до в, то М(х) будет счит след формулой М(х)= 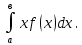 F(x)—плотность. F(x)—плотность.Если х принимает значения на всей числовой оси, то М(х)= 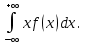 29. Дисперсия непрерывной и дискретной случайной величины, и ее свойства. Среднеквадратичное отклонение. Мат ожид характеризует СВ. Дисперсия характеризует разброс значений Св(рассеивание около ее мат ожид) Дисперсия СВ—это мат ожид квадратов отклонения СВ от ее мат ожид D(x)=Dx=M((x-m(x)^2). Т.е если х дискретная Св, то мы можем составить для нее таблицу Тогда D(x) находится след образом: D(x)=(x1-m(x))^2p1+…+(xn-m(x))^2pn Свойства: D(x) =x1^2p1+...+xn^2pn-m^2. Для дискретной Пример: М(х)=100; х1=99;х2=101; р1=0,5;р2=0,5; М(у)=100; х1=0;х2=200;р1=0,5;р2=0,5. 1).D(x)=(99-100)^2-0,5+(101-100)^2-0,5=1 По свойству: D(x)=99^2*0,5+101^2*0,5-100^2=1 2).D(y) тут лучше по св-ву. D(y)=0^2*0,5+200^2*0,5-100^2=20000-10000=10000/ Получим, что в 1 случае отклонение от среднего значения D(x)=1,а во втором случае =10 000. Недостаток дисперсии- это ее размерность, она не совпадает с размерностью СВ, в отличие от мат ожид. Ее размерность—это квадрат размерности СВ( если СВ измеряется например в рублях, то дисперсия в рублях^2). На практике это неудобно, так как мы не можем узнать велечину разброса. С этой целью вводится еще одна характеристика СВ. Среднее квадратичное отклонение—это числовая характеристика СВ имеющая вид б= 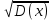 30. Сумма случайных величин: закон распределения, математическое ожидание и дисперсия. Пример. Пусть в резе опыта примет свои значения сразу 2 СВ. Суммой СВ X иY наз СВ X+Y для которой верно, если х принимает некоторые значения х1, а у некоторые значения у1, то Х+У=Х1+У1. Пример: студент сдает 2 экза. Св Х—оценка по первому экзу, СВ У—оценка по 2-му; Св Х+У=сумма оценок по первому и второму экзу. Свойства: Пусть Х и У независимые СВ(т.е их законы распределения не зависят друг от друга) Тогда: М(Х+У)=М(Х)+М(У); D(X)+D(Y) Основные законы распределения СВ В теории вероятности построен ряд моделей распределения вер СВ, которые в некоторых условиях хорошо описывают исследуемые закономерности. Для каждой такой модели(закона расспределения) есть условия, при выполнении котрых ее можно применить. Т.е если при исследовании некоторого явления оно удовлетворяет условия данной модели, то эту модель можно применить к данным исследованиям и использовать все значения о ней( M(x), D(x),б). 31. Биномиальное распределение дискретной случайной величины. Математическое ожидание, дисперсия и среднеквадратичное отклонение. Пример. Используется схема опытов Бернули. проводится n одинаковых независимых опытов В резе каждого из которых событие А может наступить с одной и той же вероятностью Р. Число наступления события А в n опытах это и есть СВ х. Х может принимать все мат знач от 0 до N. Законом распределения этой СВ может яв формула, связывающая m—число появлений события А в конкретной серии из n опытов с вероятностью того, что Х=m. Такая вер, а следовательно, закон распределения задается формулой Бернули. Р(х=м)=p(m,n,p)= 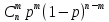 M(x)=np; D(x)=np(1-p); бх= 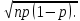 Пример: крысы подходят к лабиринту где могут выбрать 1 и0 3 дорогс одинаковой вер.К лабиринту подходят 5 крыс. Найти: 1) среднее число крыс, что подойдут к 1 дороге; 2)вер того, что ко 2 дороге подойл 3 крысы и не больше 1 крысы. Х1-число крыс к 1 дороге; х2-ко 2 дороге; х3-ко 3 дороге. Вер того, что крыса пойдет по 1, по 2 либо по 3= 1\3. N=5, р=1\3. М(х1)=5 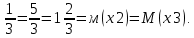 Р(х=3)= 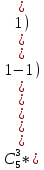 . .32. Распределение Пуассона. Применение. Математическое ожидание, дисперсия и среднеквадратичное отклонение. Пример. Распределение Пуассона—это предельный случай биномиального распределения Х.p-->0;n- 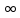 ; λ =np<=10. ; λ =np<=10.По закону Пуассона распределения числа так называемых редких явлений( число запросов в телефону компанию за 1 мин, число несчаст случ производстве, количесвто ошибки печати) Число появления события Аза выбранный промежуток времени t подчин Зак Пуассона: Р(Х=м)= 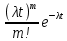 . . |
