Имитационное моделирование. отчет. 1 Предварительный анализ 6 1 Анализ имитационных моделей 6

Название	1 Предварительный анализ 6 1 Анализ имитационных моделей 6
Анкор	Имитационное моделирование
Дата	07.03.2022
Размер	0.98 Mb.
Формат файла
Имя файла	отчет.docx
Тип	Реферат #386144

Содержание

Введение 4

1 Предварительный анализ 6

1.1 Анализ имитационных моделей 6

1.2 Выбор состава технических и программных средств, обеспечивающих выполнение проектируемой системы 9

2 Технологический раздел 12

2.1 Постановка задачи 12

2.2 Описание входных и выходных данных 14

2.3 Обоснование выбора среды разработки 15

2.4 Описание функциональной схемы 18

2.5 Проектирование 20

2.6 Тестирование 31

Заключение 35

Список использованных источников 36

Введение

Модель – это любой образ, аналог, мысленный или установленный, изображение, описание, схема, чертеж, и т.п. какого-либо объекта, процесса или явления, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.

Моделирование – это исследование какого-либо объекта или системы объектов путем построения и изучения их моделей. А также – это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

Модель является средством для изучения сложных систем.

В общем случае сложная система представляется как многоуровневая конструкция из взаимодействующих элементов, объединяемых в подсистемы различных уровней. К сложным системам, в т.ч., относятся информационные системы. Проектирование таких сложных систем осуществляется в два этапа.

1). Внешнее проектирование.

На этом этапе проводят выбор структуры системы, основных ее элементов, организации взаимодействия между элементами, учет воздействия внешней среды, оценка показателей эффективности системы.

2). Внутреннее проектирование – проектирование отдельных элементов системы.

Типичным методом исследования сложных систем на первом этапе является моделирование их на ЭВМ.

В результате моделирования получаются зависимости, характеризующие влияние структуры и параметров системы на ее эффективность, надежность и другие свойства. Эти зависимости используются для получения оптимальной структуры и параметров системы.

Модель, сформулированная на языке математики с использованием математических методов называется математической моделью.

Имитационное моделирование – воспроизведение на компьютере (имитация) процесса функционирования исследуемой системы. Для него не требуется приведение математической модели к виду, разрешимому относительно искомых величин.

Для имитационного моделирования характерно воспроизведение явлений, описываемых математической моделью, с сохранением их логической структуры, последовательности чередования во времени. Для оценки искомых величин может быть использована любая подходящая информация, циркулирующая в модели, если только она доступна для регистрации и последующей обработке.

Искомые величины при исследовании процессов методом имитационного моделирования обычно определяют как средние значения по данным большого числа реализаций процесса. Если число реализаций N, используемых для оценки искомых величин, достаточно велико, то в силу закона больших чисел получаемые оценки приобретают статистическую устойчивость и с достаточной для практики точностью могут быть приняты в качестве приближенных значений искомых величин.

В качестве среды разработки выбрана Embarcadero RAD Studio XE2 (C++), а также среда имитационная моделирования GPSS World.

Цель работы – разработка имитационной модели м помощью языков высокого уровня и специального языка имитационного программирования, разобрать этапы моделирования, сравнить результаты и сделать вывод об использовании специальных сред имитационного моделирования.

1 Предварительный анализ

1.1 Анализ имитационных моделей

За последние десятилетия в самых разных областях народного хозяйства возникла необходимость решения вероятностных задач, связанных с работой систем массового обслуживания (СМО). Примерами таких систем служат телефонные станции, ремонтные мастерские, торговые предприятия, билетные кассы и т.д. Работа любой системы массового обслуживания состоит в обслуживании поступающего в нее потока требований (вызовы абонентов, приход покупателей в магазин, требования на выполнение работы в мастерской и т. д.).

Математическая дисциплина, изучающая модели реальных систем массового обслуживания, получила название теории массового обслуживания.

Задача теории массового обслуживания – установить зависимость результирующих показателей работы СМО (вероятности того, что требование будет обслужено; математического ожидания числа обслуженных требований и т. д.) от входных показателей (количество приборов в системе, параметров входящего потока требований и т. д.). Установить такие зависимости в формульном виде можно только для простых систем массового обслуживания.

Изучение же реальных систем проводится путем имитации, или моделирования их работы на ЭВМ с привлечением метода статистических испытаний.

Система массового обслуживания считается заданной, если определены:

1) входящий поток требований, или, иначе говоря, закон распределения, характеризующий моменты времени поступления требований в систему.

Первопричину требований называют источником. В дальнейшем условимся считать, что источник располагает неограниченным числом требований и что требования однородны, т. е. различаются только моментами появления в системе;

2) система обслуживания состоит из накопителя и узла обслуживания. Последний представляет собой одно или несколько обслуживающих устройств, которые в дальнейшем будем называть приборами. Каждое требование должно поступить на один из приборов, чтобы пройти обслуживание.

Может оказаться, что требованиям придется ожидать, пока приборы освободятся. В этом случае требования находятся в накопителе, образуя одну или несколько очередей. Положим, что переход требования из накопителя в узел обслуживания происходит мгновенно;

3) время обслуживания требования каждым прибором, которое является случайной величиной и характеризуется некоторым законом распределения;

4) дисциплина ожидания, т. е. совокупность правил, регламентирующих количество требований, находящихся в один и тот же момент времени в системе. Система, в которой поступившее требование получает отказ, когда все приборы заняты, называется системой без ожидания.

Если требование, заставшее все приборы занятыми, становится в очередь и ожидает до тех пор, пока освободиться один из приборов, то такая система называется чистой системой с ожиданием.

Система, в которой требование, заставшее все приборы занятыми, становится в очередь только в том случае, когда число требований, находящихся в системе, не превышает определенного уровня (в противном случае происходит потеря требования), называется смешанной системой обслуживания;

5) дисциплина обслуживания, т. е. совокупность правил, в соответствии с которыми требование выбирается из очереди для обслуживания. Наиболее часто на практике используются следующие правила:

заявки принимаются к обслуживанию в порядке очереди;
заявки принимаются к обслуживанию по минимальному времени получения отказа;
заявки принимаются к обслуживанию в случайном порядке в соответствии с заданными вероятностями;

6) дисциплина очереди, т.е. совокупность правил, в соответствии с которыми требование отдает предпочтение той или иной очереди (если их несколько) и располагается в выбранной очереди. Например, поступившее требование может занять место в самой короткой очереди; в этой очереди оно может расположиться последним (такая очередь называется упорядоченной), а может пойти на обслуживание вне очереди. Возможны и другие варианты.

Введем также следующие характеристики потока событий:

регулярность; поток называется регулярным, если события следуют одно за другим через равные промежутки времени;
стационарность; поток называется стационарным, если его вероятностные характеристики не зависят от времени
отсутствие последействия; поток называется потоком без последействия, если для любых не пересекающихся отрезков времени число событий, попадающих на один участок не зависит от числа событий, попадающих на другой
ординарность; если события в потоке появляются поодиночке, а не группами, то поток называется ординарным.

Имитационное моделирование систем массового обслуживания

Сущность метода имитационного моделирования применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы, при помощи которых можно вырабатывать случайные реализации заданных потоков однородных событий, а также моделировать процессы функционирования обслуживающих систем. Эти алгоритмы используются для многократного воспроизведения реализации случайного процесса обслуживания при фиксированных условиях задачи. Получаемая при этом информация о состоянии процесса подвергается статистической обработке для оценки величин, являющихся показателями качества обслуживания.

При исследовании сложных систем методом имитационного моделирования существенное внимание уделяется учету случайных факторов.

В качестве математических схем, используемых для формализации действия этих факторов, используются случайные события, случайные величины и случайные процессы (функции). Формирование на ЭВМ реализаций случайных объектов любой природы сводится к выработке и преобразованию случайных чисел. Рассмотрим способ получения возможных значений случайных величин с заданным законом распределения. Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат случайные величины, имеющие равномерное распределение в интервале (0, 1). Другими словами, возможные значения xi случайной величины ξ, имеющей равномерное распределение в интервале (0,1), могут быть преобразованы в возможные значения yi случайной величины η, закон распределения которой задан. Способ преобразования состоит в том, что из равномерно распределенной совокупности отбираются случайные числа, удовлетворяющие некоторому условию таким образом, чтобы отобранные числа подчинялись заданному закону распределения.

1.2 Выбор состава технических и программных средств, обеспечивающих выполнение проектируемой системы

GPSS (англ. General Purpose Simulation System — система моделирования общего назначения) — язык моделирования, используемый для имитационного моделирования различных систем, в основном систем массового обслуживания.

Система GPSS была разработана сотрудником фирмы IBM Джефри Гордоном в 1961 году. Гордоном были созданы 5 первых версий языка: GPSS (1961), GPSS II (1963), GPSS III (1965), GPSS/360 (1967) и GPSS V (1971). Известный ранее только специалистам, в нашей стране этот программный пакет завоевал популярность после издания в СССР в 1980 году монографии Т Дж. Шрайбера. В ней была рассмотрена одна из ранних версий языка — GPSS/360, а также основные особенности более мощной версии — GPSS V, поддерживаемой компанией IBM, у нас она была более известна как пакет моделирования дискретных систем (ПМДС). Этот пакет работал в среде подсистемы диалоговой обработки системы виртуальных машин единой серии (ПДО СВМ ЕС) ЭВМ. После окончания поддержки GPSS V компанией IBM следующей версией стала система GPSS/H компании Wolverine Software разработанная в 1978 году под руководством Дж. Хенриксена. В 1984 году появилась первая версия GPSS для персональных компьютеров с операционной системой DOS — GPSS/PC. Она была разработана компанией Minuteman Software под руководством С. Кокса. Конец XX века ознаменовался разработкой компанией Minuteman Software программного продукта GPSS World, увидевшей свет в 1993 году. За сравнительно небольшой период времени было выпущено несколько его версий, причем в каждой последующей возможности системы моделирования наращивались. Помимо этих основных версий существует также Micro-GPSS, разработанная Ингольфом Сталлом в Швеции, — это упрощенная версия, предназначенная для изучения языка GPSS, и WebGPSS, также предназначенная для изучения работы системы и разработки простейших имитационных моделей в сети интернет.

Система GPSS изучается во многих учебных заведениях в России и за рубежом. Широко используется для решения практических задач. Динамическим элементом модели является транзакт — абстрактный объект, который перемещается между статическими элементами, воспроизводя различные события реального моделируемого объекта. В процессе работы модели накапливается статистика, автоматически выводимая по завершении процесса моделирования. Статические элементы модели: источники транзактов, устройства, очереди и другие. Их расположение в модели определяется блоками.

В программе на языке GPSS достаточно сложно представить непосредственно процессы обработки данных на уровне алгоритмов. Кроме того, модель представляет собой программу, а значит не имеет графической интерпретации, что затрудняет процесс разработки модели и снижает наглядность модели в целом.

.

2 Технологический раздел

2.1 Постановка задачи

Разработку можно разбить на подзадачи:

Анализ предметной области

Модель – это любой образ, аналог, мысленный или установленный, изображение, описание, схема, чертеж, и т.п. какого-либо объекта, процесса или явления, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.

Моделирование – это исследование какого-либо объекта или системы объектов путем построения и изучения их моделей. А также – это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

Модель является средством для изучения сложных систем.

В общем случае сложная система представляется как многоуровневая конструкция из взаимодействующих элементов, объединяемых в подсистемы различных уровней. К сложным системам, в т.ч., относятся информационные системы. Проектирование таких сложных систем осуществляется в два этапа.

1). Внешнее проектирование.

На этом этапе проводят выбор структуры системы, основных ее элементов, организации взаимодействия между элементами, учет воздействия внешней среды, оценка показателей эффективности системы.

2). Внутреннее проектирование – проектирование отдельных элементов системы.

Типичным методом исследования сложных систем на первом этапе является моделирование их на ЭВМ.

В результате моделирования получаются зависимости, характеризующие влияние структуры и параметров системы на ее эффективность, надежность и другие свойства. Эти зависимости используются для получения оптимальной структуры и параметров системы.

Модель, сформулированная на языке математики с использованием математических методов называется математической моделью.

Имитационное моделирование – воспроизведение на компьютере (имитация) процесса функционирования исследуемой системы. Для него не требуется приведение математической модели к виду, разрешимому относительно искомых величин.

Для имитационного моделирования характерно воспроизведение явлений, описываемых математической моделью, с сохранением их логической структуры, последовательности чередования во времени. Для оценки искомых величин может быть использована любая подходящая информация, циркулирующая в модели, если только она доступна для регистрации и последующей обработке.

Искомые величины при исследовании процессов методом имитационного моделирования обычно определяют как средние значения по данным большого числа реализаций процесса. Если число реализаций N, используемых для оценки искомых величин, достаточно велико, то в силу закона больших чисел получаемые оценки приобретают статистическую устойчивость и с достаточной для практики точностью могут быть приняты в качестве приближенных значений искомых величин.

Формулировка задачи, подлежащая реализации:

Требуется провести моделирование работы автозаправочной станции (АЗС) в течении 8 часов.

Параметры АЗС:

число колонок 2-3;

поток автомобилей, поступающих на заправку, подчиняется экспоненциальному закону с параметрами λ=0 мин. и β=6,5 мин.

(1)

время заправки на первой колонке 10±2,5 мин.
время заправки на второй и третьей колонке подчиняется экспоненциальному закону с параметрами λ=4 мин. и β мин. (разумное значение β установить самостоятельно) или 13±4 мин.;
автомобиль подъезжает к свободной колонке.

Требуется определить следующие параметры работы АЗС в течение 8 часов:

коэффициент загрузки каждой колонки;
среднее время обслуживания каждой колонкой;
максимальное и среднее число автомобилей в очереди к каждой колонке;
среднее время нахождения автомобиля в каждой очереди.

И реализация модели с помощью языка высокого уровня и языка имтационного моделирования, сделать выводы об эффективности разработки и предпочтении в реализации.

2.2 Описание входных и выходных данных

До того как приступить к формулированию алгоритмов решения поставленной задачи и представлению их в виде программы, необходимо проанализировать требования к функциональным и рабочим характеристикам разрабатываемой системы, определить структуру входных и выходных данных.

tgeneral – текущее время в системе. Программа имитирует работу систему пока Tgeneral < 8 часов (480 минут)

t – случайная величина, распределенная по экспоненциальному закону распределения с параметрами λ=0 мин. и β=5 мин. Определяет моменты поступления заявок в СМО

t1 – случайная величина, определяющая время обслуживания заявки колонкой 1 (каналом 1), распределена на интервале 10±2,5

t2 – случайная величина, определяющая время обслуживания заявки колонкой 2 (каналом 2), распределенная по экспоненциальному закону распределения с параметрами λ=0 мин. и β=4,5 мин.

t3 – случайная величина, определяющая время обслуживания заявки колонкой 2 (каналом 2), распределенная по экспоненциальному закону распределения с параметрами λ=0 мин. и β=4,5 мин.

twait1, twait2, twait3 – время ожидания автомобилем своей очереди к каждой из колонок соответственно

sum_twait1, sum_twait2, sum_twait3 – суммарное время ожидания всех автомобилей в соответствующей очереди (очереди к соответствующей колонке)

tengaged1, tengaged2, tengaged3 – время, на которое каждая из колонок занята и не может временно обслуживать другие заявки

sum_t1, sum_t2, sum_t3 – суммарное время работы (непосредственно обслуживания) каждой из колонок

queue1, queue2, queue3 – количество автомобилей в очереди в данный момент времени

max1, max2, max3 – максимальная очередь к каждой колонке соответственно

quancar1, quancar2, quancar3 – количество, автомобилей, обслуженных каждой из колонок соответственно

length_queue1, length_queue2, length_queue3 – сумма длин очередей для каждой из колонок соответсвенно

q1, q2, q3 – счетчики состояний для каждой очереди соответственно

2.3 Обоснование выбора среды разработки

Программа разработана в Embarcadero RAD Studio XE2, в среде C++. Embarcadero RAD Studio — среда быстрой разработки приложений (RAD) для Microsoft Windows фирмы Embarcadero Technologies. Embarcadero RAD Studio XE2 – это комплексное решение для быстрой разработки приложений Windows®, .NET, веб-приложений и приложений баз данных. Оно включает в себя Delphi, C++Builder и Delphi Prism, позволяя создавать приложения для различных платформ Windows и баз данных до 5 раз быстрее. Инструменты RAD Studio значительно ускоряют создание приложений для настольных компьютеров, рабочих станций, сенсорных дисплеев, информационных терминалов и Интернета, поэтому их использует уже более 2 миллионов разработчиков. В состав этих средств входят быстрые компиляторы, визуальная среда для разработки приложений с пользовательским интерфейсом, платформа визуальных компонентов (VCL), а также обширные возможности для подключения к базам данных и службам. Сообщество партнеров и разработчиков предлагает тысячи дополнительных компонентов для каждого конкретного приложения, технологии, функции или задачи. Больше ни одно решение не обладает необходимой функциональностью, гибкостью и управляемостью для разработки качественных, высокопроизводительных приложений для такого количества платформ, источников данных, типов ПО, архитектур и пользователей.

GPSS (англ. General Purpose Simulation System — система моделирования общего назначения) — язык моделирования, используемый для имитационного моделирования различных систем, в основном систем массового обслуживания.

Система GPSS была разработана сотрудником фирмы IBM Джефри Гордоном в 1961 году. Гордоном были созданы 5 первых версий языка: GPSS (1961), GPSS II (1963), GPSS III (1965), GPSS/360 (1967) и GPSS V (1971). Известный ранее только специалистам, в нашей стране этот программный пакет завоевал популярность после издания в СССР в 1980 году монографии Т Дж. Шрайбера. В ней была рассмотрена одна из ранних версий языка — GPSS/360, а также основные особенности более мощной версии — GPSS V, поддерживаемой компанией IBM, у нас она была более известна как пакет моделирования дискретных систем (ПМДС). Этот пакет работал в среде подсистемы диалоговой обработки системы виртуальных машин единой серии (ПДО СВМ ЕС) ЭВМ. После окончания поддержки GPSS V компанией IBM следующей версией стала система GPSS/H компании Wolverine Software разработанная в 1978 году под руководством Дж. Хенриксена. В 1984 году появилась первая версия GPSS для персональных компьютеров с операционной системой DOS — GPSS/PC. Она была разработана компанией Minuteman Software под руководством С. Кокса. Конец XX века ознаменовался разработкой компанией Minuteman Software программного продукта GPSS World, увидевшей свет в 1993 году. За сравнительно небольшой период времени было выпущено несколько его версий, причем в каждой последующей возможности системы моделирования наращивались. Помимо этих основных версий существует также Micro-GPSS, разработанная Ингольфом Сталлом в Швеции, — это упрощенная версия, предназначенная для изучения языка GPSS, и WebGPSS, также предназначенная для изучения работы системы и разработки простейших имитационных моделей в сети интернет.

Система GPSS изучается во многих учебных заведениях в России и за рубежом. Широко используется для решения практических задач. Динамическим элементом модели является транзакт — абстрактный объект, который перемещается между статическими элементами, воспроизводя различные события реального моделируемого объекта. В процессе работы модели накапливается статистика, автоматически выводимая по завершении процесса моделирования. Статические элементы модели: источники транзактов, устройства, очереди и другие. Их расположение в модели определяется блоками.

В программе на языке GPSS достаточно сложно представить непосредственно процессы обработки данных на уровне алгоритмов. Кроме того, модель представляет собой программу, а значит не имеет графической интерпретации, что затрудняет процесс разработки модели и снижает наглядность модели в целом.

2.4 Описание функциональной схемы

Согласно поставленной задаче разрабатываем следующую имитационную модель.

АЗС функционирует в течении 8 часов (480 минут). АЗС имеет три колонки – 3 канала обслуживания.

Поток автомобилей, поступающих на заправку – поток заявок – случаен, ординарен и подчиняется экспоненциальному закону распределения. Это говорит о необходимости получения случайных чисел, распределенных по экспоненциальному закону распределения. Воспользуемся методом обратных функций, описанным выше.

Время заправки на первой колонке 10±2,5 мин. Это означает необходимость генерации случайного числа на интервале (0,1) и дальнейшее его сдвижение на интервал (7,5 , 12,5). Для этого воспользуемся следующей формулой 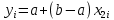(2):

(2)

Время заправки на второй и третьей колонке подчиняется экспоненциальному закону. Для получения случайных чисел, распределенных по экспоненциальному закону воспользуемся методом, описанным выше.

Результатом имитации работы АЗС будут следующие параметры:

коэффициент загрузки каждой колонки;
среднее время обслуживания каждой колонкой;
максимальное и среднее число автомобилей в очереди к каждой колонке;
среднее время нахождения автомобиля в каждой очереди.

Представим схему функционирования каждой колонки (рис.1).

Представим алгоритм функционирования модели (рис.2), причем представим наиболее общий случай, когда каждая из колонок уже имеет очередь заявок.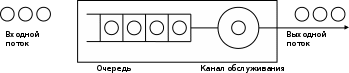

Рисунок 1 – Схема функционирования каждой колонки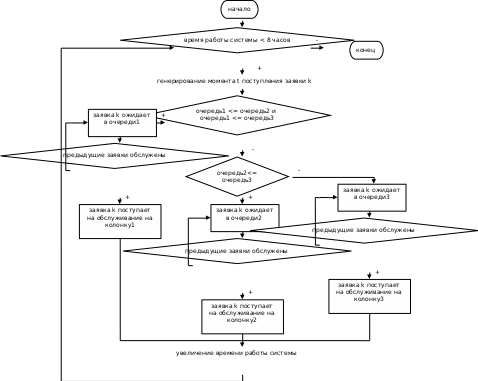

Рисунок 2 – Алгоритм функционирования модели

2.5 Проектирование

Проектирование осуществлялось в двух средах Embarcadero RAD Studio XE2 (среда разработки приложений C++ Builder на языке программирования высокого уровня) и GPSS World – среда имитационного моделирования. Сравнение процессов проектирования производиться с целью выявления таких факторов как простота и эффективность.

Рассмотрим процесс проектирования в C++ Builder.

При запуске проекта открывается главное окно приложения, представленное на рисунке 3:

Рисунок 3 – Главное окно приложения

Для моделирования необходимо выбрать пункт меню Моделирование, произойдет переход на следующую форму, в которой отражен результат моделирования с учетом условий моделирования по описанному выше алгоритму (рисунок 4):

Рисунок 4 – Результат моделирования

Код главной формы:

/---------------------------------------------------------------------------

#include

#pragma hdrstop

#include "Unit1.h"

#include "Unit2.h"

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//---------------------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//---------------------------------------------------------------------------

void __fastcall TForm1::N2Click(TObject *Sender)

{

Form2->Show(); //переход на форму с результатом моделирования

}

//---------------------------------------------------------------------------
void __fastcall TForm1::N3Click(TObject *Sender)

{

Application->Terminate(); // прекращение работы приложения

}

//---------------------------------------------------------------------------

Код формы с результатами моделирования:

//---------------------------------------------------------------------------

#include

#pragma hdrstop

#include "Unit2.h"

#include

#include

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm2 *Form2;

//---------------------------------------------------------------------------

//реализация алгоритма имитационной модели в конструкторе формы

__fastcall TForm2::TForm2(TComponent* Owner)

: TForm(Owner)

{

//объявление переменных

float tgeneral,t,t1,t2,t3,

twait1,twait2, twait3,

sum_twait1,sum_twait2,sum_twait3,

tengaged1,tengaged2,tengaged3,

sum_t1,sum_t2,sum_t3;

int queue1,queue2,queue3,max1,max2,max3,

quancar1,quancar2,quancar3,

length_queue1,length_queue2,length_queue3,

q1,q2,q3;

//обнуление переменных

tgeneral=0;

queue1=0; queue2=0; queue3=0;

max1=0; max2=0; max3=0;

tengaged1=0; tengaged2=0; tengaged3=0;

twait1=0; twait2=0; twait3=0;

sum_twait1=0; sum_twait2=0; sum_twait3=0;

quancar1=0; quancar2=0; quancar3=0;

sum_t1=0; sum_t2=0; sum_t3=0;

length_queue1=0; length_queue2=0; length_queue3=0;

q1=1;q2=1;q3=1;

randomize(); //генератор случайных чисел

//реализация алгоритма по схеме

while (tgeneral<480)

{

t=fabs(5*log(5*rand()/100000.0));

if ((queue1<=queue2) && (queue1<=queue3) )

{

t1=fabs(7.5+rand()/100000.0*(12.5-7.5));

sum_t1=sum_t1+t1;

queue1=queue1++;

length_queue1=length_queue1+queue1;

q1=q1++;

if (max1
if (tengaged1>tgeneral)

twait1=tengaged1-tgeneral+t1;

else twait1=0;

sum_twait1=sum_twait1+twait1;

tengaged1=tgeneral+t1;

quancar1=quancar1++;

}

else

{

if (queue2<=queue3)

{

t2=fabs(4-4*log(4*rand()/100000.0));

sum_t2=sum_t2+t2;

queue2=queue2+1;

length_queue2=length_queue2+queue2;

q2=q2++ ;

if (max2
if (tengaged2>tgeneral)

twait2=tengaged2+t2-tgeneral;

else twait2=0;

sum_twait2=sum_twait2+twait2;

tengaged2=tgeneral+t2;

quancar2=quancar2+1;

}

else

{

t3=fabs(4-4.5*log(4.5*rand()/10000.0));

sum_t3=sum_t3+t3;

queue3=queue3++;

length_queue3=length_queue3+queue3;

q3=q3++;

if (max3
if (tengaged3>tgeneral)

twait3=tengaged3+t3-tgeneral;

else twait3=0;

sum_twait3=sum_twait3+twait3;

tengaged3=tgeneral+t3;

quancar3=quancar3++;

}

}

if ((tengaged1
{

queue1=queue1--;

length_queue1=length_queue1+queue1;

q1=q1++;

}

if ((tengaged2
{

queue2=queue2--;

length_queue2=length_queue2+queue2;

q2=q2++;

}

if ((tengaged3
{

queue3=queue3--;

length_queue3=length_queue3+queue3;

q3=q3++;

}

tgeneral=tgeneral+t;

} /*прорисовка таблицы StringGrid и заполнение ее подсчитанными значениями*/

StringGrid1->ColWidths[0] = 500;

StringGrid1->Cells[1][0]="Колонка 1";

StringGrid1->Cells[2][0]="Колонка 2";

StringGrid1->Cells[3][0]="Колонка 3";

StringGrid1->Cells[0][1]="Коэффициент загрузки";

StringGrid1->Cells[0][2]="Среднее время обслуживания, мин";

StringGrid1->Cells[0][3]="Максимальное число автомобилей в очереди, шт";

StringGrid1->Cells[0][4]="Среднее число автомобилей в очереди, шт";

StringGrid1->Cells[0][5]="Среднее время нахождения автомобиля в очереди, мин";

StringGrid1->Cells[1][1]=FloatToStr(floor(sum_t1/480*1000)/1000);

StringGrid1->Cells[2][1]=FloatToStr(floor(sum_t2/480*1000)/1000);

StringGrid1->Cells[3][1]=FloatToStr(floor(sum_t3/480*1000)/1000);

StringGrid1->Cells[1][2]=FloatToStr(floor(sum_t1/quancar1*1000)/1000);

StringGrid1->Cells[2][2]=FloatToStr(floor(sum_t2/quancar2*1000)/1000);

StringGrid1->Cells[3][2]=FloatToStr(floor(sum_t3/quancar3*1000)/1000);

StringGrid1->Cells[1][3]=IntToStr(max1);

StringGrid1->Cells[2][3]=IntToStr(max2);

StringGrid1->Cells[3][3]=IntToStr(max3);

StringGrid1->Cells[1][4]=FloatToStr(floor(length_queue1/q1));

StringGrid1->Cells[2][4]=FloatToStr(floor(length_queue2/q2));

StringGrid1->Cells[3][4]=FloatToStr(floor(length_queue3/q3));

StringGrid1->Cells[1][5]=FloatToStr(floor(sum_twait1/quancar1*1000)/1000);

StringGrid1->Cells[2][5]=FloatToStr(floor(sum_twait2/quancar2*1000)/1000);

StringGrid1->Cells[3][5]=FloatToStr(floor(sum_twait3/quancar3*1000)/1000); }

Рассмотрим процесс проектирования в GPSS World.

Построение имитационной модели начнем с создания заголовка модели, который может быть представлен, например, в таком виде:

; GPSSW AZS.GPS

********************************************************

* Моделирование автомобильной заправочной станции (АЗС)*

********************************************************

Моделирование потока машин, поступающих на заправку, будем выполнять с помощью оператора GENERATE (Генерировать). Нам необходимо сформировать поток машин, поступающих на обслуживание на АЗС, который подчиняется экспоненциальному распределению вероятностей. Это можно сделать, используя встроенные распределения вероятностей.

В системе GPSSW в библиотеку процедур включено более 20 встроенных распределений вероятности. Эти распределения имеют широкий диапазон использования.

Каждый вызов процедуры распределения вероятности требует, чтобы вы определили параметр потока, номер генератора случайных чисел.

GENERATE (Exponential(1,0,6.5))

Автомобиль, поступающий на заправку, сначала встает в очередь, если она есть. Это можно промоделировать оператором QUEUE (Очередь), который только в совокупности с оператором DEPART (Выйти) собирает статистическую информацию о работе моделируемой очереди.

QUEUE Zapravka

Поскольку на АЗС есть две колонки для заправки, то автомобиль подъезжает к первой колонке, если она свободна, и ко второй, если первая занята. Если обе колонки заняты, то автомобиль ожидает их освобождения в общей очереди. Направление автомобилей на ту или иную колонку может быть обеспечено оператором TRANSFER (Передать).

TRANSFER Both,Kol_1,Kol_2

Слово Both (Оба) означает возможность передачи требования (машины) по двум направлениям: к оператору с меткой Kol_1, если первая колонка (объект) не занята, и к оператору с меткой Kol_2, если занята.

Следуя логике, автомобиль может выйти из очереди только тогда, когда освободится первая или вторая колонка (объект). Для моделирования используются два сегмента. Первый из них связан с работой первой колонки, а второй – с работой второй. Оба сегмента начинаются с оператора SEIZE (Занять), и каждый из них имеет свою метку, соответственно Kol_1 и Kol_2, которые определяют занятость первой или второй колонки (канала обслуживания). При освобождении одной из них находящееся впереди требование выходит из очереди и идет в канал на обслуживание.

Начало первого сегмента записывается так:

Kol_1 SEIZE Kolonka_1

Выход автомобиля из очереди фиксируется оператором DEPART с соответствующим названием очереди.

DEPART Zapravka

Далее должно быть промоделировано время заправки автомобиля. Оно в нашем примере составляет 10±2,5 мин. Для моделирования этого процесса используется оператор ADVANCE (Задержать), который в нашей задаче будет выглядеть так:

ADVANCE 10,2.5

Затем необходимо сообщить об освобождении колонки под номером 1. Это можно сделать с помощью оператора RELEASE (Освободить). Он в нашей задаче записывается так:

RELEASE Kolonka_1

Далее используется оператор TRANSFER (Передать) в режиме безусловной передачи требования к оператору с указанной меткой в поле операнда В.

TRANSFER ,Next

Начало второго сегмента запишется так:

Kol_2 SEIZE Kolonka_2

Выход автомобиля из очереди фиксируется оператором DEPART с соответствующим названием очереди.

DEPART Zapravka

Далее должно быть промоделировано время заправки автомобиля. Оно в нашем примере составляет 13±4 мин. Для моделирования этого процесса используется оператор ADVANCE, который в нашей задаче будет выглядеть так:

ADVANCE 13,4

После заправки автомобиль покидает колонку.

Далее необходимо сообщить об освобождении колонки под номером 2. Это можно сделать с помощью оператора RELEASE. Он в нашей задаче записывается так:

RELEASE Kolonka_2

Затем используем оператор SAVEVALUE (Сохраняемая величина) с меткой Next (Следующий) для сохранения среднего времени нахождения автомобиля в очереди под именем Zapravka в сохраняемой величине под именем Ave_Queue.

Next SAVEVALUE Ave_Queue,QT$Zapravka

Далее автомобиль покидает АЗС. Для этого используется оператор TERMINATE (Завершить):

TERMINATE

И наконец, мы должны создать сегмент, который будет моделировать работу АЗС в течение рабочей смены, равной 8 ч. Поскольку моделирование работы АЗС про водится в минутах, то время моделирования системы будет равно 8 × 60 = 480 мин. Этот сегмент будет выглядеть так:

GENERATE 480

TERMINATE 1

START 1

Следует особо подчеркнуть, что парные операторы QUEUE и DEPART для каждой очереди должны иметь одно и то же, но свое уникальное имя. Это же от носится и к операторам SEIZE и RELEASE.

Завершающим оператором в нашей задаче является START, дающий команду начать моделирование:

START 1

Код программы:

; GPSSW AZS.GPS

********************************************************

* Моделирование автомобильной заправочной станции (АЗС)*

********************************************************

INFORM QTABLE Zapravka,0,3,35
GENERATE (Exponential(1,0,6.5)) ; Поступление автомобилей на заправку

QUEUE Zapravka ; Вход автомобиля в очередь на заправку

TRANSFER Both,Kol_1,Kol_2 ; Переход автомобиля к свободной колонке
Kol_1 SEIZE Kolonka_1 ; Определение занятости 1 колонки

DEPART Zapravka ; Выход автомобиля из очереди на заправку

ADVANCE 10,2.5 ; Заправка автомобиля на 1 колонке

RELEASE Kolonka_1 ; Освобождение 1 колонки

TRANSFER ,Next ; Переход к оператору с меткой Next
Kol_2 SEIZE Kolonka_2 ; Определение занятости 2 колонки

DEPART Zapravka ; Выход автомобиля из очереди на заправку

ADVANCE 13,4 ; Заправка автомобиля на 2 колонке

RELEASE Kolonka_2 ; Освобождение 2 колонки

Next SAVEVALUE Ave_Queue,QT$Zapravka ; Сохранение времени пребывания в очереди

TERMINATE ; Выход автомобиля из системы

GENERATE 480 ; Моделирование АЗС в течение смены

TERMINATE 1

START 1

2.6 Тестирование

При компиляции не выявлено ошибок и предупреждений. Успешная компиляция проекта представлена на рисунках 5 и 6.

Рисунок 5 – Успешная компиляция

Рисунок 6 – Запущенный проект

После создания имитационную модель необходимо оттранслировать и запустить на выполнение. Для этого:

щелкните по пункту Command главного меню системы или нажмите комби нацию клавиш Alt+C. Появится выпадающее меню;
щелкните по пункту Create Simulation (Создать выполняемую модель) вы падающего меню.

Так как в имитационной модели имеется управляющая команда START, то исходная имитационная модель будет транслироваться, и если в ней нет ошибок, начнется процесс моделирования системы (рисунок 7).

Рисунок 7 – Трансляция исходной имитационной модели

Отчет моделирования системы представлен на рисунке 8.

Рисунок 8 – Отчет моделирования системы

Окно REPORT содержит следующую информацию:

В верхней строке указывается:

START TIME (Начальное время) – 0.000;

END TIME (Время окончания) – 480.000;

BLOCKS (Число блоков) – 16;

FACILITIES (Число каналов обслуживания) – 2;

STORAGES (Число накопителей) – 0.

Ниже указываются результаты моделирования каналов обслуживания соответственно под назначенными нами именами KOLONKA_1 и KOLONKA_2:

ENTRIES (Число входов) – 45 и 33;

UTIL. (Коэффициент использования) – 0.901 и 0.875;

AVE. TIME (Среднее время обслуживания) – 9.608 и 12.734;

AVAIL. (Доступность) – 1 и 1;

OWNER (Возможное число входов) – 78 и 79;

PEND – 0 и 0;

INTER – 0 и 0;

RETRY (Повтор) – 5 и 5;

DELAY (Отказ) – 0 и 0.

Еще ниже указываются результаты моделирования очереди под именем ZAPRAVKA:

MAX (Максимальное содержание) – 10;

CONT. (Текущее содержание) – 5;

ENTRY (Число входов) – 83;

ENTRY(0) (Число нулевых входов) – 13;

AVE.CONT. (Среднее число входов) – 3.494;

AVE.TIME (Среднее время пребывания в очереди) – 20.209;

AVE.( 0) – 23.962;

RETRY – 0.

Еще ниже приведены параметры сохраняемой величины под именем AVE_QUEUE:

RETRY – 0;

VALUE (Значение) – 20.173.

Заключение

Цель работы – изучить имитационное моделирование, рассмотреть вопросы его применения на практике, а также реализовать имитационную модель автозаправки на языке высокого уровня и языке имитационного моделирования, сделать выводы об эффективности.

Имитационное моделирование – воспроизведение на компьютере (имитация) процесса функционирования исследуемой системы. Для него не требуется приведение математической модели к виду, разрешимому относительно искомых величин.

Для имитационного моделирования характерно воспроизведение явлений, описываемых математической моделью, с сохранением их логической структуры, последовательности чередования во времени. Для оценки искомых величин может быть использована любая подходящая информация, циркулирующая в модели, если только она доступна для регистрации и последующей обработке.

Инструментальной средой разработки выбрана визуальная среда программирования Embarcadero RAD Studio XE2(С++ Builder) и среда имитационного моделирования GPSS World.

Проведя анализ процесса проектирования можно сделать вывод о том что использование визуальных сред делает приложение наглядным, но лишает математическую модель точности, язык имитационного моделирования будет интересен для более подробного изучения модели. Рекомендуем использовать при возможности оба способа, так как они имеют различные цели: первый – наглядность, второй – точность модели.

Список использованных источников

Алпатов Ю.Н. Моделирование процессов и систем управления: Учебное пособие / Ю.Н. Алпатов. ‑ СПб.: Лань, 2018. ‑ 140 c.
Баксанский О.Е. Моделирование в науке: Построение физических моделей / О.Е. Баксанский. ‑ М.: Ленанд, 2019. ‑ 160 c.
Булыгина О.В. Имитационное моделирование в экономике и управлении: Учебник / О.В. Булыгина, А.А. Емельянов, Н.З. Емельянова. ‑ М.: Инфра-М, 2017. ‑ 447 c.
Волгина О.А. Математическое моделирование экономических процессов и систем: Учебное пособие / О.А. Волгина, Н.Ю. Голодная, Н.Н. Одияко. ‑ М.: КноРус, 2016. ‑ 395 c.
Кораблев, Ю.А. Имитационное моделирование (для бакалавров) / Ю.А. Кораблев. ‑ М.: КноРус, 2018. ‑ 59 c.
Угольницкий Г.А., Управление эколого-экономическими системами / Г.А. Угольницкий. – Москва: Вузовская книга, 2016.