КУРСАЧ. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Расчет линейных однофазных электрических цепей переменного тока Исходные данные для выполнения расчета: R1 = 4 Ом; Xl2 = 6 Ом; R2 = 10 Ом; R3 = 7 Ом; Xc1 = 3 Ом; U = 20 В. 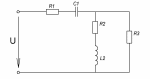 Рисунок 3.1 - Схема для расчета однофазной электрической цепи переменного тока Расчет линейной однофазной электрической цепи переменного тока методом проводимостей Рассчитаем сопротивления: XL2 = ω L2 = 314,16 · 19,1 · 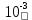 6 Ом, 6 Ом,XС1 = 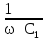 = = 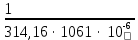 3 Ом, 3 Ом,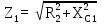 = = 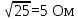 , ,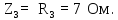 Рассчитаем проводимости на параллельном участке цепи. Активные проводимости: g2 = 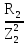 = = 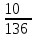 = 0,0735294 Cм, = 0,0735294 Cм,g3 = 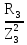 = = 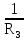 = = 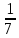 = 0,1428577 Cм, = 0,1428577 Cм,Реактивные проводимости: b2 = 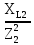 = = 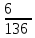 = 0,0441176 См, = 0,0441176 См,b3 = 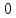 См. См.Полную проводимость на участке 23 определим по формуле y23 = 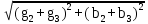 = = 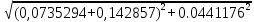 = == 0,220838 См, у2 = 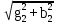 = 0,0857493 См, = 0,0857493 См,у3 = 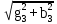 = 0,142857 См. = 0,142857 См.Рассчитаем полное сопротивление участка 23: Z23 = 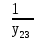 = = 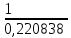 = 4,52821 Ом. = 4,52821 Ом.Определим активное и реактивное сопротивления параллельного участка R23 = 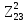 · g23 = 4,528212 · (0,0735294+0,142857) = 4,43694 Ом, · g23 = 4,528212 · (0,0735294+0,142857) = 4,43694 Ом,X23 = 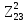 · b23 = 4,528212 · 0,0441176 = 0,904618 Ом. · b23 = 4,528212 · 0,0441176 = 0,904618 Ом.Расчет линейной однофазной электрической цепи переменного тока символическим методом На основании вышеизложенного рассчитаем схему, изображенную на рисунке 3.1. Начертим схему замещения однофазной цепи переменного тока (рисунок 3.2). 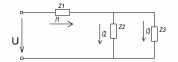 Рисунок 3.2 - Схема замещения однофазной цепи переменного тока Комплексы сопротивлений участков (по номерам токов) и полного сопротивления цепи будут равны: 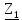 = R1 - j = R1 - j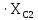 = 4 - j·3 = 5· = 4 - j·3 = 5·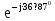 Ом, Ом,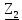 = R2 + j = R2 + j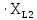 = 10 + j·6 = 11,6619· = 10 + j·6 = 11,6619·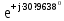 Ом, Ом,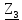 = R3 - j = R3 - j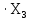 =7 + j·0 =7 + j·0 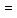 7· 7·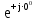 Ом. Ом.Комплекс сопротивления участка 23 цепи: 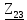 = =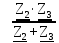 = =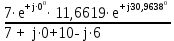 = = 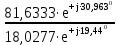 = == 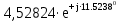 =4,43693+ j·0,904623 Ом, =4,43693+ j·0,904623 Ом,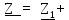 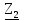 = 4 - j·3 + 4,43693+ j·0,904623 = 8.69824· = 4 - j·3 + 4,43693+ j·0,904623 = 8.69824·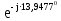 , ,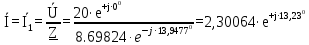 , ,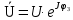 = 20 = 20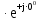 , ,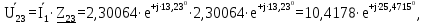 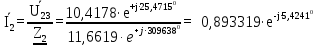 , ,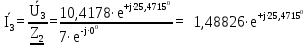 . .Расчет мощностей S, P, Q однофазной электрической цепи переменного тока. Баланс мощностей Комплекс полной мощности расчетной цепи: 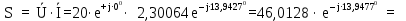 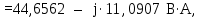 Sист. =90,5642 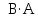 ; Q = ; Q =  21,8292 вар; P = 87,894 Вт, 21,8292 вар; P = 87,894 Вт,Pпотр. = 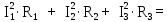 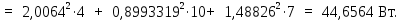 Баланс мощностей сходится, следовательно, токи однофазной электрической цепи рассчитаны верно. 4 Методика расчета трехфазных цепей переменного тока Расчет трехфазной цепи переменного тока при соединении фаз приемника звездой Таблица 4.1 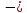 Исходные данные Исходные данные
Линейное напряжение сети Uлин = 380 В. Расчет сопротивления элементов схемы замещения приемников. № 1: Найдем sin1. cos 1 =0,70 , отсюда 1 = arccos 0,7 =45,570, sin45.570 = 0,71411, sin1=0,714143. Z1 = 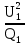 · sin 1 = · sin 1 =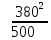 · 0,714143 = 206,244 Ом, · 0,714143 = 206,244 Ом,R1 = Z1 · cos1 = 206,244 · 0,7 = 144,3708 Ом, X1 = Z1 · sin1 = 206,244 · 0,71411 = 147,288 Ом, 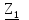 = R1 + j · X1 = Z1 · = R1 + j · X1 = Z1 · 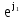 = 144,3708 + j·147,288 = 206,244· = 144,3708 + j·147,288 = 206,244·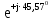 Ом. Ом.№ 2: Найдем sin2. cos 2 =0,70 , отсюда 2 = arccos 0,7=45,570, sin45.570 = 0,71411, sin2=0,71411. Z2 = 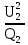 · sin2 = · sin2 =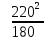 · 0,71411 = 192,016 Ом, · 0,71411 = 192,016 Ом,R2 = Z2 · cos2 = 192,016 · 0,7 = 134,411 Ом, X2 = Z2 · sin2 =192,016 · 0,71411 = 137,121 Ом, 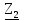 = R2 + j · 0 = Z2 · = R2 + j · 0 = Z2 · 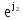 = 134,411 + j ·137,121 = 192,016 · = 134,411 + j ·137,121 = 192,016 ·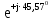 Ом. Ом.№ 3: Найдем sin1. cos 1 =0,70 , отсюда 1 = arccos 0,7 =45,570, sin45.570 = 0,71411, sin1=0,714143. Z3 = 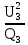 · sin 3 = · sin 3 =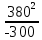 · (-0,714143) = 344,741 Ом, · (-0,714143) = 344,741 Ом,R3 = Z3 · cos3 = 343,741 · 0,7 = 240,619 Ом, X3 = Z3 · sin3 = 343,741 ·( 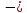 0,714143) = 0,714143) = 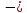 245,480229 Ом, 245,480229 Ом,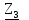 = R3 + j · X3 = Z3 · = R3 + j · X3 = Z3 · 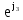 = 240,619 = 240,619 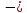 j·245,480229 = j·245,480229 = = 344,741· 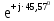 Ом. Ом.Схема включения приемников в трехфазную сеть По условию задачи Uлин = Uф, 380 В = 380 В, следовательно, приемники нужно соединить треугольником. Чертим схему включения приемников в трехфазную сеть (рисунок 4.1) Р 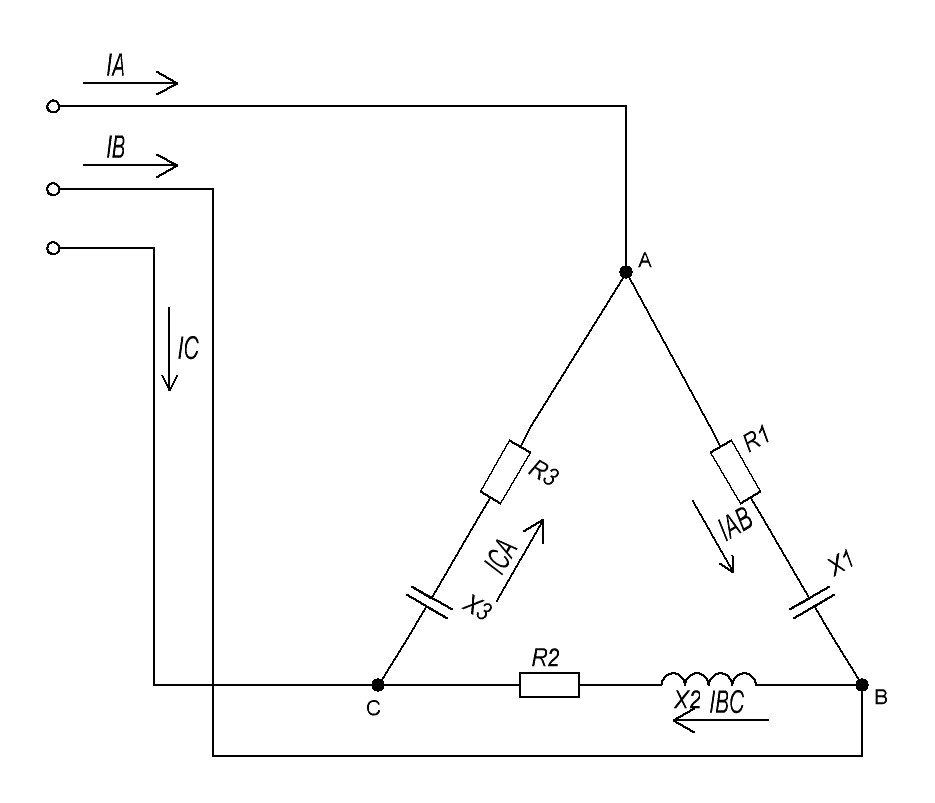 исунок 4.1  Схема включения приемников треугольником Схема включения приемников треугольникомРасчет фазных и линейных токов каждого приемника Определяем комплексные действующие значения фазных (они же линейные) напряжений: 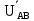 = 3800 · = 3800 · 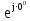 В; В; 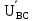 = 3800 · = 3800 · 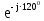 В; В; 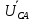 = 380 · = 380 · 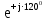 В. В.Находим фазные токи: 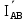 = = 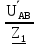 = = 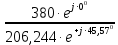 = 1,84248· = 1,84248·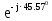 = 1,2848 - j · 1,31573 A, = 1,2848 - j · 1,31573 A,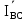 = = 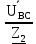 = = 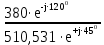 = 0,744323· = 0,744323·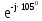 = -0,71846 - j · 0,192645 A, = -0,71846 - j · 0,192645 A,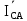 = = 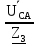 = = 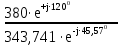 = 1,10548· = 1,10548·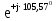 = == -1,07061 + j · 0,275482 A. Находим фазные токи: 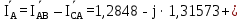 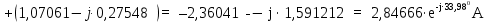 , ,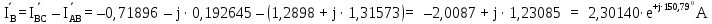 , ,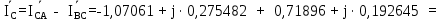 = 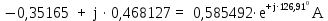 . .Расчет мощностей Определим активную, реактивную и полную мощности. Активная мощность: P = 490,098 + 294,9059 + 200 = 984,157 Вт. Реактивная мощность: Q =500 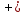 200 200 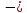 300 = 400 вар. 300 = 400 вар.Полная мощность: S= 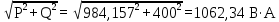 Расчет трехфазной цепи символическим методом при соединении приемников звездой и треугольником Таблица 4.2 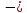 Исходные данные Исходные данные
Линейное напряжение сети Uлин = 220 В. Расчет сопротивления элементов схемы замещения приемников № 1: По условию задачи cos 1 не дан, значит 1 найдем через tg1 = = 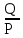 , следовательно tg1 = , следовательно tg1 = 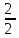 = 1, 1 = arctg1= = 1, 1 = arctg1= 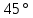 . .Z1 = 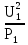 · cos1 = · cos1 =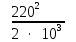 · cos · cos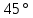 = 17,1120 Ом, = 17,1120 Ом,R1 = Z1 · cos1 = 17,1120 · 0,707107 = 12,1000 Ом, X1 = Z1 · sin1 = 17,1120 · 0,707107 = 12,1000 Ом, чисто активная нагрузка, 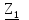 = R1 + j · X1 = Z1 · = R1 + j · X1 = Z1 · 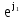 = 12,1000 + j · 12,1000 = = 12,1000 + j · 12,1000 == 17,1120· 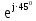 Ом. Ом.№ 2: По условию задачи cos 1 не дан, значит 1 найдем через tg1 = = 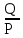 , следовательно tg1 = , следовательно tg1 = 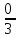 = 0, 2 = arctg0= = 0, 2 = arctg0= 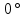 . .Z2 = 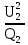 · sin 2 = · sin 2 =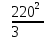 · 1 = 16,13333 Ом, · 1 = 16,13333 Ом,R2 = Z2 · cos2 = 16,13333 · 1 = 16,13333 Ом, X2 = Z2 · sin2 = 16,13333 · 0 = 0 Ом, 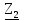 = R2 + j · X2 = Z2 · = R2 + j · X2 = Z2 · 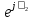 = 16,13333 - j · 0 = 16,13333 · = 16,13333 - j · 0 = 16,13333 ·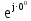 Ом. Ом.№ 3: По условию задачи cos 3 = 1, следовательно 3= arccos 1 = 00 sin3 = 0. Z3 = 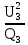 · cos 3 = · cos 3 =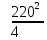 · 1 = 12,100 Ом, · 1 = 12,100 Ом,R3 = Z3 · cos3 = 12,100 · 1 = 12,100 Ом, X3 = Z3 · sin3 = 12,100 · 0 = 0 Ом, 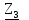 = R3 + j · X3 = Z3 · = R3 + j · X3 = Z3 · 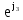 = 12,100 + j · 0 = 12,100 · = 12,100 + j · 0 = 12,100 ·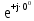 Ом. Ом.№ 4: По условию задачи cos 4 = 0, следовательно 3= arccos 0 = -900 sin4 = -1. Z4 = 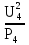 · sin4 = · sin4 =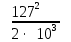 · -1 = 8,0645 Ом, · -1 = 8,0645 Ом,R4 = Z4 · cos4 = 0 Ом, X4 = Z4 · sin4 = 8,0645 · -1 = -8,0645 Ом, 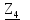 = R4 + j · X4 = Z4 · = R4 + j · X4 = Z4 · 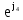 = 0 - j · 8,0645 = 8,0645 · = 0 - j · 8,0645 = 8,0645 ·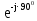 Ом. Ом.Схема включения приемников в трехфазную сеть Схема включения приемников определяется в зависимости от их номинального напряжения Uном и линейного напряжения трехфазной сети Uлин. Если Uном = Uлин, то используется соединение треугольником. Если Uлин = 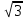 · Uном - звездой. · Uном - звездой. Таким образом, приемники № 1, № 2 и № 3 необходимо соединить треугольником, так как Uном = Uлин = 220 В. Трехфазный симметричный приемник № 4 необходимо соединить звездой, так как по условию задачи 220 В = 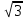 ·127 В. ·127 В. Схема включения приемников к трехфазной цепи приведена на рисунке 4.5. Расчет фазных и линейных токов приемника, токов в проводах сети 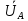 = 127 · = 127 · 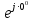 В; В;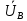 = 127 · = 127 · 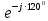 В; В;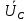 = 127 · = 127 · 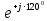 В. В.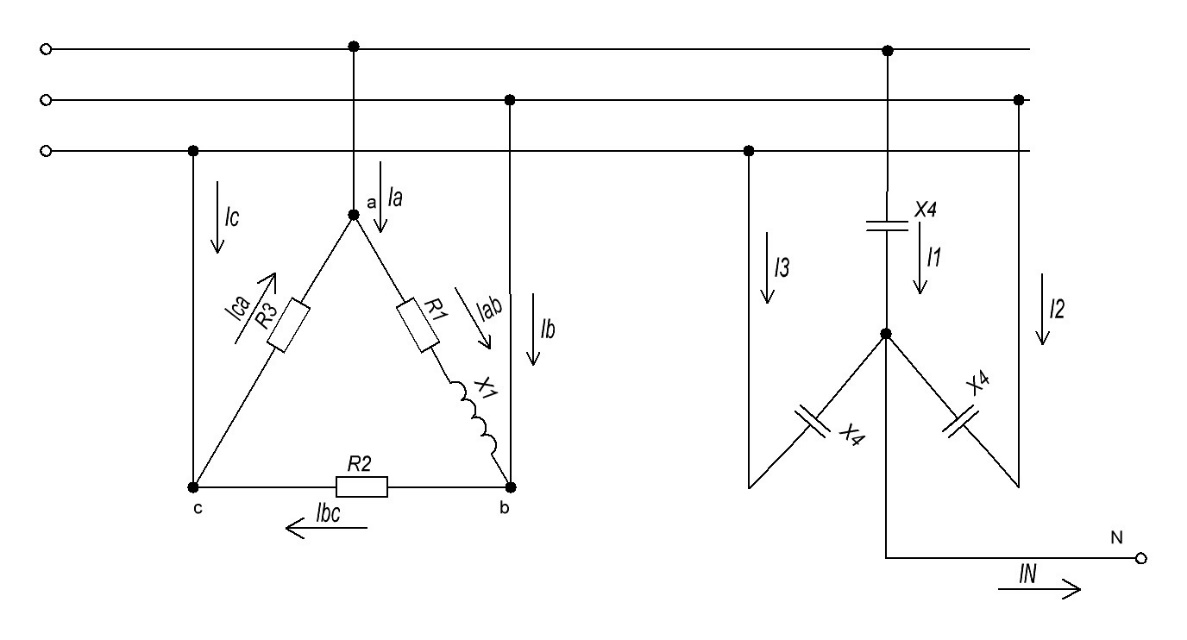 Рисунок 4.2  Схема включения приемников к трехфазной цепи Схема включения приемников к трехфазной цепиЛинейные напряжения сети (они же и фазные напряжения приемников, соединенных треугольником) равны: 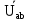 = 220 · = 220 · 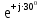 В; В;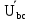 = 220 · = 220 · 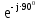 В; В; 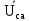 = 220 · = 220 · 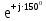 В. В.Фазные токи (они же линейные токи) приемников № 1, № 2, № 3 равны: 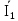 = = 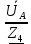 = = 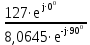 = 15,7480 · = 15,7480 ·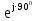 = 0 + j · 15,748 A, = 0 + j · 15,748 A,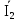 = = 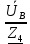 = = 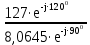 = 15,7480 · = 15,7480 ·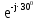 = 13,6382 - j · 7,874 A, = 13,6382 - j · 7,874 A,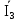 = = 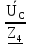 = = 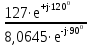 = 15,7480 · = 15,7480 · 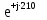 = -13,6381 - j · 7,874 A. = -13,6381 - j · 7,874 A.Ток в нулевом проводе: 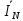 = = 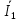 + + 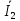 + + 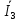 = 0 - j · 15,748 + 13,6382 - j · 7,874 + -13,6381 - j · 7,874= = 0 - j · 15,748 + 13,6382 - j · 7,874 + -13,6381 - j · 7,874== 0 A. Определим фазные токи симметричного приемника: 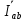 = = 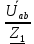 = = 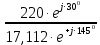 = 12,8565 · = 12,8565 ·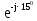 = = = 12,4184 - j · 3,32751 A, 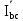 = = 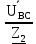 = = 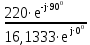 = 13,26364 · = 13,26364 ·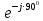 = 0 - j · 13,6364 A, = 0 - j · 13,6364 A,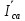 = = 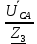 = = 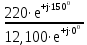 = 18,1818 · = 18,1818 ·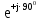 = 0 + j · 105,263 A. = 0 + j · 105,263 A.Рассчитаем линейные токи симметричного приемника: 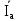 = = 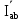 - - 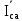 = 12,4184 - j · 3,32751 + 15,7459 - j · 9,0909 = 28,1643 - j · ·12,41841 = 30,7806 · = 12,4184 - j · 3,32751 + 15,7459 - j · 9,0909 = 28,1643 - j · ·12,41841 = 30,7806 · 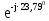 A, A,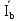 = = 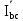 - - 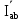 = 0 - j · 13,6364 - 12,4184 - j · 3,32751 = = 0 - j · 13,6364 - 12,4184 - j · 3,32751 = = - 12,4184 - j · 10,30889 = 16,1397 · 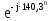 A, A,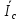 = = 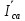 - - 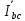 = 27,6489 · = 27,6489 · 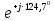 A. A.Построение векторной диаграммы напряжений, совмещенной с векторной диаграммой токов. Для построения векторной диаграммы выбираем масштаб напряжений и токов: M (U) = 55 В/см, М (I) = 50 А/см. Рассчитаем длины векторов напряжений: l(UA) = 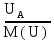 = = 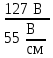 = 2,3 см, = 00, = 2,3 см, = 00,l(UB) = 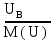 = = 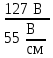 = 2,3 см, = –1270, = 2,3 см, = –1270,l(UC) = 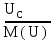 = = 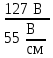 = 2,3 см, = +1200, = 2,3 см, = +1200,l(UAB) = 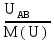 = = 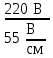 = 4 см, = +300, = 4 см, = +300,l(UBC) = 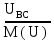 = = 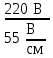 = 4 см, = – 900, = 4 см, = – 900,l(UCA) = 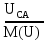 = = 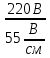 = 4 см, = +1500. = 4 см, = +1500.Рассчитаем длины векторов токов: l(I1) = 3,1 см, = +900, l(I2) = 3,1 см, = -300, l(I3) = 3,1 см, = +2100, l(Iab) =2,6 см, = – 1500, l(Ibc) = 2,7 см, = –900, l(Ica) = 3,6см, = +1500. Линейные токи симметричного приемника №4 определяем разностью фазных токов: 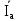 = = 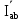 - - 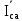 ; ; 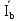 = = 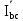 - - 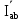 ; ;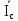 = = 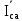 - - 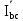 . .При этом построенные векторы токов 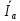 , , 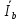 , , 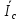 должны совпасть с расчетными значениями: должны совпасть с расчетными значениями:l(Ia) = 6,2 см, = – 240, l(Ib) = 3,3 см, = –1400, l(Ic) = 5,5 см, = +1250.  Расчет трехфазной цепи при соединении приемников звездой и треугольником графоаналитическим методом Таблица 4.4 — Исходные данные
Линейное напряжение сети Uлин = 127 В. Схема включения приемников к трехфазной сети Схема включения приемников определяется в зависимости от их номинального напряжения Uном и линейного напряжения трехфазной сети Uлин. Если Uном = Uлин, то используется соединение треугольником. Если Uлин = 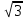 · Uном - звездой. · Uном - звездой. Таким образом, приемники № 1, № 2 и № 3 необходимо соединить звездой, так как по условию задачи 380 В = 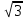 ·220 В. ·220 В. Поскольку приемники несимметричны, то необходим нулевой провод, который обеспечивает равенство по величине фазных напряжений приемников. Трехфазный симметричный приемник № 4 необходимо соединить треугольником, так как Uном = Uлин = 380 В. Схема включения приемников в трехфазную цепь приведена на рисунке 4.6. 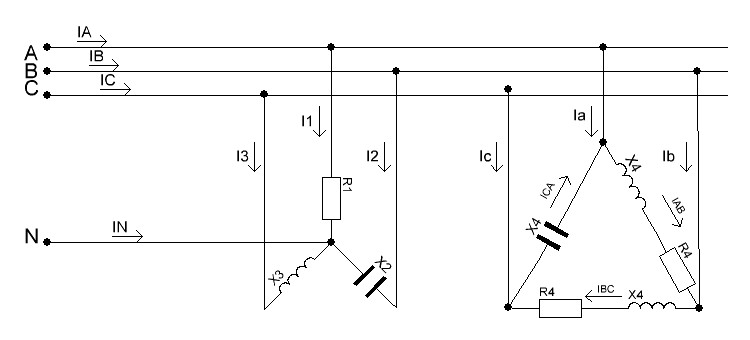 Рисунок 4.6 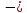 Схема включения приемников в трехфазную цепь Схема включения приемников в трехфазную цепьФазные напряжения приемников № 1, № 2, № 3, благодаря нулевому проводу, равны: UA = UB = UC = 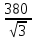 = 220 В. = 220 В.Определим sin1 и sin2, а также углы 1, 2 и 3: 1 = arctg1 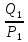 = arctg = arctg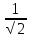 = 45 = 45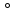 , ,2 = arctg2 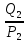 = arctg = arctg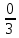 = 0 = 0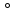 , ,3 = arccos3 = arccos 1 = 0 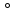 . .Найдем фазные токи приемников № 1, № 2 и № 3: Iab = 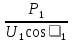 = = 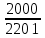 = 12,8565 A, = 12,8565 A,Ibc = 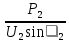 = = 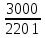 = 13,6364 A, = 13,6364 A,Ica = 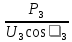 = = 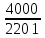 = 18,1818 A. = 18,1818 A.Рассчитаем фазные токи приемника № 4: I1 = I2 = I3 = 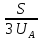 = = 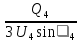 = =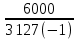 = 15,748 A. = 15,748 A.Найдем 4: sin4 = 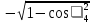 = = 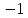 4 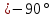 Следовательно, построив симметричную трехлучевую звезду фазных напряжений и отложив вдоль векторов этих напряжений фазные токи (так как A = C = 00, B = 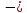 900), можно определить вектор тока в нулевом проводе, геометрически сложив эти токи. 900), можно определить вектор тока в нулевом проводе, геометрически сложив эти токи.Выбираем масштаб напряжений и токов: M (U) = 55 В/см, М (I) = 5 А/см. Рассчитаем длины векторов напряжений: l(UA) = 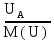 = = 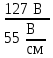 = 2,3 см, = 00, = 2,3 см, = 00,l(UB) = 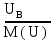 = = 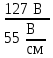 = 2,3 см, = -1200, = 2,3 см, = -1200,l(UC) = 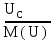 = = 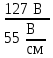 = 2,3 см, = +1200, = 2,3 см, = +1200,l(UAB) = 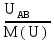 = = 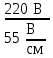 = 4 см, = +300, = 4 см, = +300,l(UBC) = 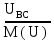 = = 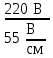 = 4 см, = - 900, = 4 см, = - 900,l(UCA) = 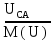 = = 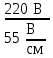 = 4 см, = +1500. = 4 см, = +1500.Рассчитаем длины векторов токов: l(I1) = 3,1 см, 1= 00 l(I2) = 3,1 см, 1= - 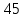 0 0l(I3) = 3,1 см, 3= 900 Ток в нейтральном проводе: IN = l(IN)  М (I) = 0 A. М (I) = 0 A.Длины фазных токов: l(Iab) =2,6 см, = +600; l(Ibc) = 2,7 см, = +600; l(Ica) = 3,6 см, = +600. Линейные токи симметричного приемника №4 определяем разностью фазных токов: 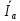 = = 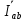 - - 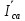 ; ;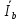 = = 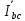 - - 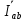 ; ;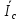 = = 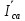 - - 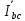 . .При этом построенные векторы токов 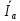 , , 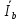 , , 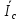 должны совпасть с расчетными значениями: должны совпасть с расчетными значениями:l(Ia) = 6,2 см; l(Ib) = 3,2 см; l(Ic) = 5,5 см; l(IA) = 6,7 см; l(IB) = 2 см; l(IC) = = 5,7 см, Ia= l(Ia)  М (I) = 6,2 см М (I) = 6,2 см  5 А/см = 31 A, 5 А/см = 31 A,Ib= l(Ib)  М (I) = 3,2 см М (I) = 3,2 см  5 А/см = 16 A, 5 А/см = 16 A,Ic= l(Ic)  М (I) = 5,5 см М (I) = 5,5 см  5 А/см = 27,5 A. 5 А/см = 27,5 A. |
