КУРСАЧ. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
 СОДЕРЖАНИЕ Введение 3 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов 4 2 Расчет сложных электрических цепей постоянного тока 8 3 Расчет линейных однофазных электрических цепей переменного тока 17 4 Расчет трехфазных электрических цепей переменного тока при соединении фаз приемника звездой или треугольником 21 5 Расчет трехфазных электрических цепей переменного тока при соединении фаз приемника звездой и треугольником. 26 6 Расчет нелинейных электрических цепей переменного тока 34 Заключение 38 Список использованных источников 39 ВВЕДЕНИЕ Электротехникой в широком смысле слова называется обширная область практического применения электромагнитных явлений. Широкое и разнообразное использование электрической энергии объясняется тем, что она имеет огромное преимущество перед другими формами энергии. Только на базе электричества оказалось возможным широкое развитие новейших научно-технических направлений в радиоэлектронике, в технике связи, в области компьютерных технологий. Трудно представить жизнь современного человека без использования электрической энергии. Курс Теоретических основ электротехники (ТОЭ) в обобщенной форме рассматриваются теория и методы расчета разнообразных электромагнитных явлений. Данный курс занимает основное место среди общетехнических дисциплин, определяющих теоретический уровень профессиональной подготовки инженеров-электриков, является теоретической базой для последующего изучения специальных дисциплин. Включение дисциплины ТОЭ в государственный образовательный стандарт объясняется тем, что принцип работы всех рабочих машин, используемых в области машиностроения, и построение устройств управления ими, базируется на основных фундаментальных понятиях данной дисциплины. В ходе изучения курса электротехники учащимся необходимо изучить и выработать навыки решения электрических цепей постоянного и переменного токов различными методами. Расчет простых электрических цепей постоянного тока со смешанным соединением сопротивлений методом эквивалентных преобразований Для схемы электрической цепи, изображенной на рисунке 1.1, определить токи в ветвях цепи методом эквивалентных преобразований, составить баланс мощностей. Исходные данные представлены в таблице 1.1.
Р 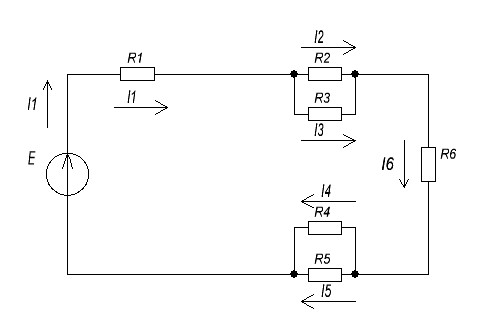 исунок 1.1 – Схема электрической цепи постоянного тока Сопротивления R2и R3 соединены параллельно, следовательно, сопротивление R23равно: R23 = 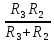 = = 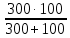 = 75 Ом, = 75 Ом,Свернем исходную схему (рисунок 1.1). Получаем схему цепи, изображенную на рисунке 1.2. Р 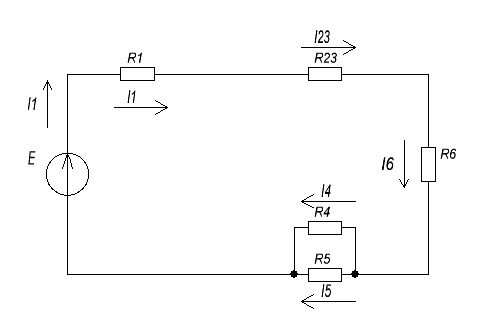 исунок 1.2 – Преобразованная схема электрической цепи постоянного тока Сопротивления R4и R5 соединены параллельно, следовательно, сопротивление R45равно: R45 = 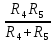 = = 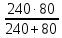 = 60 Ом, = 60 Ом,Свернем исходную схему (рисунок 1.1). Получаем схему цепи, изображенную на рисунке 1.3. Р 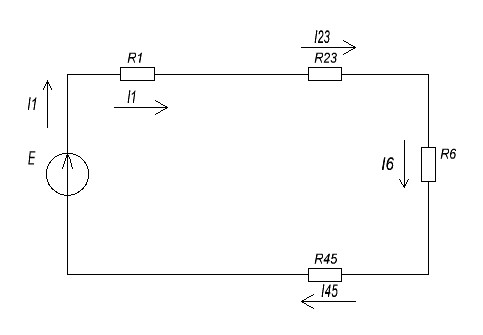 исунок 1.3 – Преобразованная схема электрической цепи постоянного тока В схеме цепи сопротивления R1, R23, R6, R45соединены последовательно, следовательно, общее сопротивление цепи можно рассчитать по формуле R = R1 + R23 + R6 + R45 = 15 + 75 + 10 + 60 = 160 Ом, Получаем схему цепи, изображенную на рисунке 1.4. Р 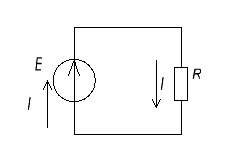 исунок 1.4 – Преобразованная схема электрической цепи постоянного тока Определяем токи в ветвях электрической цепи. По закону Ома для схемы цепи, изображенной на рисунке 2.4, ток I равен: I = 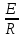 = = 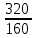 = 2 А, = 2 А,Разворачиваем схему, изображенную на рисунке 1.4, и переходим к схеме, приведенной на рисунке 2.3 и 2.2. I = I1 - I6 = I45 = I23 = 2 А, Для определения токов в других ветвях цепи находим напряжения на этих ветвях. Напряжение U23 для схемы цепи, изображенной на рисунке 1.2, определим по закону Ома: U23 = I23 R23 = 75 2 = 150 = U2 = U3 В, Напряжение U45 для схемы цепи, изображенной на рисунке 1.3, определим по закону Ома: U45 = I45 R45 = 60 2 = 120 В = U4 = U5, По закону Ома в схеме цепи, приведенной на рисунке 1.2: I2 = 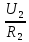 = = 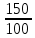 = 1,5 А, = 1,5 А,I3 = 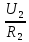 = = 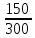 = 0,5 А, = 0,5 А,По закону Ома в схеме цепи, приведенной на рисунке 1.3: I4 = 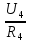 = = 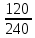 = 0.5 (А), = 0.5 (А),I5 = 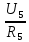 = = 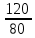 = 1.5 (А), = 1.5 (А),Составляем уравнение баланса мощностей: РИСТ = РПОТР, Мощность источника энергии равна: РИСТ = EI = 320 2 = 640 Вт, Мощность приемников энергии рассчитываем по формуле РПОТР = 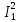 R1 + R1 + 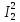 R2 + R2 + 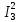 R3 + R3 + 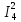 R4 + R4 + 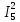 R5 - R5 - 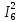 R6= R6== 22 15 + 1,52 100 + 0,52 300 + + 0,52 240 + 1,52 80 + 22 10 = 640 Вт, 640 Вт = 640 Вт, Баланс мощностей соблюдается, следовательно, токи определены правильно. Методы расчета сложных электрических цепей постоянного тока Таблица 2.1 Исходные данные
Расчет электрической цепи постоянного тока методом узловых и контурных уравнений       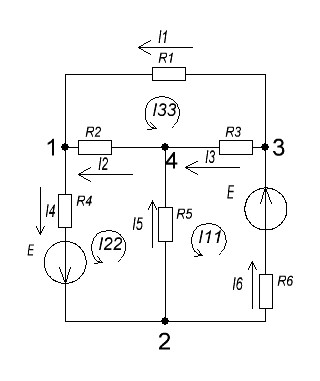 Рисунок 2.5  Принципиальная схема электрической цепи постоянного тока Принципиальная схема электрической цепи постоянного токаДля схемы, изображенной на рисунке 2.5, указываем направления действительных токов в ветвях I1, I2, I3, I4, I5, I6. В заданной цепи шесть ветвей (т = 6), значит, в системе должно быть шесть уравнений. Сначала составляем уравнения по первому закону Кирхгофа. В цепи четыре узла (n = 4), следовательно, нужно составить три уравнения (n - 1 = 4 - 1 = 3). Например, для узлов 1, 2, 3 по первому закону Кирхгофа запишем уравнения: узел 1: I1 - I4 + I2 = 0, узел 2: I4 - I5 - I6 = 0, узел 3: I6 - I5 - I1 = 0, Контур 1421 (обход против часовой стрелке): + E2 =+ I5 R5 + I2 R2 - I4 R4, Контур 2342 (обход против часовой стрелки): + E1 = +I3 R3 - I5 R5 + I6 R6, Контур 1431 (обход против часовой стрелки): 0 = I1 R1 - I2 R2 - I3 R3, Записываем уравнения для узлов и контуров в систему. Получили систему из шести уравнений с шестью неизвестными: 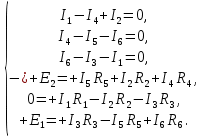 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 2.1: 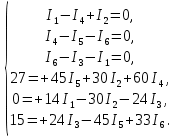 Таблица 2.2 — Коэффициенты при токах из системы уравнений
I1 = 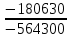 ≈ 0,32 А, ≈ 0,32 А,I2 = 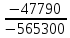 ≈ 0,0846 А, ≈ 0,0846 А,I3 = 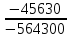 ≈ 0,0808 А, ≈ 0,0808 А,I4 = 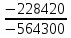 ≈ 0,4047 А, ≈ 0,4047 А,I5 = 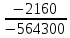 ≈ 0,0038 А, ≈ 0,0038 А,I6 = 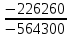 ≈ 0,4009 А, ≈ 0,4009 А,Расчет электрической цепи постоянного тока методом контурных токов Составляем уравнения для каждого контура. Контур 1431: 0 = R1 · I11 + R2 · (I11+ I22) + R4 · (I11– I33), Контур 2342: + E1 = R3 · I22 + R5 · (I22 + I33) + R2 · (I22 + I11), Контур 1421: + E2 = R6 · I33 + R5 · (I33 + I22)+ R4 · (I33 – I11), Составляем систему уравнений: 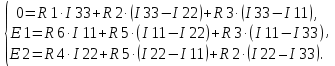 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 2.2: 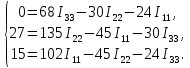 Запишем данную систему так, чтобы контурные токи во всех уравнениях располагались по порядку: 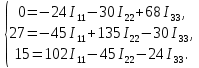 Таблица 2.3 Коэффициенты при токах из системы уравнений
Контурные токи: I11 = 0,4009 А; I22 = 0,4047 А; I33 = 0,32 А. Находим действительные токи ветвей. Контурный ток I11 имеет направление по часовой стрелке (получился со знаком «минус»). I6 = I11 = 0,6306 А, совпадает с I11, I4 = I22 = -0,1440 А, совпадает с I22, I1 = I33 = 1,4667 А, совпадает с I33, I5 = I22 - I11 = 0,4047 - 0,4009 = 0,0038 А, совпадает с I11, I2= I22 - I33 = 0,4047 - 0,32 = 0,0847 A, совпадает с I22, I3 = I11 - I33 = 0,4009 - 0,32 = 0,0809 А, не совпадает с I33, 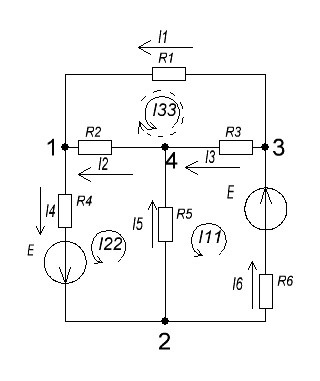 Рисунок 2.6 – Принципиальная схема электрической цепи постоянного тока Расчет электрической цепи постоянного тока методом узлового напряжения Приведем схему, изображенную на рисунке 2.6, к двум узлам, преобразовывая треугольник сопротивлений R1, R2, R4 в эквивалентную звезду сопротивлений R21, R14, R42. Новый узел обозначим А (рисунки 2.10). 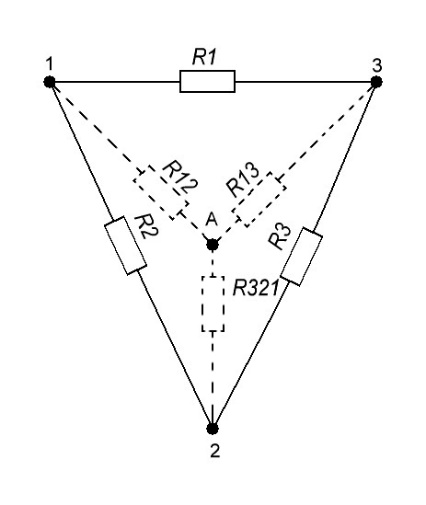 Рисунок 2.10 – Преобразование треугольника сопротивлений в звезду Р 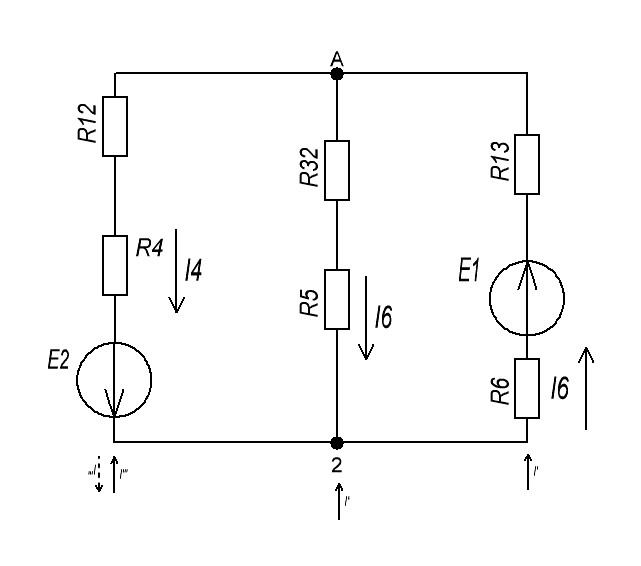 исунок 2.11 – Схема, преобразованная к двум узлам Рассчитаем величины сопротивлений эквивалентной звезды: R13 = 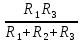 = = 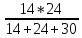 = 4,9412 Ом, = 4,9412 Ом,R12 = 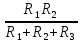 = = 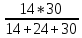 = = 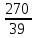 = 6,9231 Ом, = 6,9231 Ом,R14 = 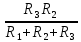 = = 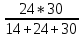 = 10,5882 Ом. = 10,5882 Ом.Выбираем направление токов в параллельных ветвях вправо: I', I", I"'. Определим общее сопротивление каждой ветви: R' =R6 + R13 = 33 + 4,9412 = 37,9412 Ом, R" = R5 + R32 = 45 + 10,5882 = 55,5882 Ом, R'" = R4 + R12 = 60 + 6,1765 = 66,1765 Ом. Рассчитаем проводимость каждой ветви: g' = 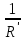 = = 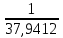 = 0,0263566 См, = 0,0263566 См,g'' = 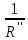 = = 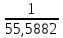 = 0,0179894 См, = 0,0179894 См,g''' = 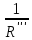 = = 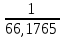 = 0,0151111 См, = 0,0151111 См,Определим узловое напряжение: UА2 = 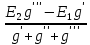 = = 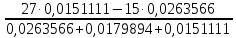 = = 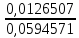 = 0,212770 В, = 0,212770 В,Расчет электрической цепи постоянного тока методом наложения токов П 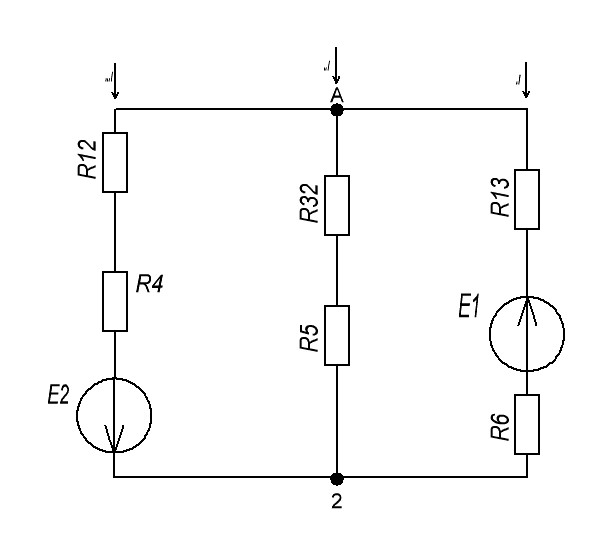 риведем исходную схему (рисунок 2.6) к двум узлам (рисунок 2.11), преобразовывая треугольник сопротивлений R1, R2, R4 в эквивалентную звезду сопротивлений R13, R12, R32. Сопротивления эквивалентной звезды рассчитаны ранее: R13 = 4,9412 Ом; R12 = 6,1765 Ом; R32 = 10,5882 Ом. Рисунок 2.13 – Схема электрической цепи, приведенная к двум узлам Для схемы электрической цепи, изображенной на рисунке 2.13, составляем расчетные схемы (рисунки 2.15, 2.16). Указываем на них направления частичных токов. Решаем первую расчетную схему (рисунок 2.15) методом эквивалентных преобразований (методом «свертывания»). Р 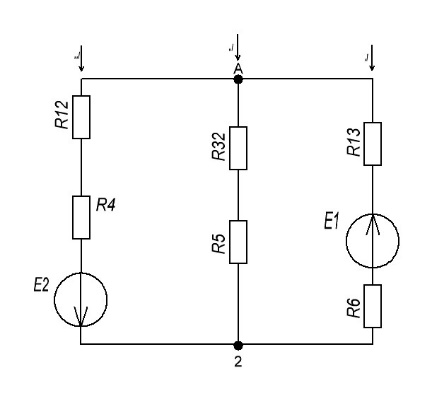 исунок 2.14 – Первая расчетная схема Находим общее сопротивление для первой расчетной схемы: R4,12,32,5,02 = 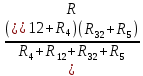 = = 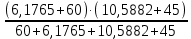 = = = 30,2110 Ом, R' = R13 + R6 + R4,12,32,5,02 = 4,9412 + 33 + 30,2110 = 68,1522 Ом. Находим общий ток для первой расчетной схемы: 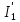 = = 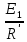 = = 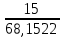 = 0,2201 (А). = 0,2201 (А). 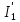 = = 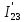 . .Рассчитываем напряжение параллельных ветвей: 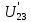 = = 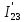 ·R4,12,32,5,02= 0,2201 ·30,2110 = 6,6494 В. ·R4,12,32,5,02= 0,2201 ·30,2110 = 6,6494 В.Определяем частичные токи на параллельных ветвях для первой расчетной схемы: 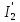 = = 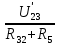 = = 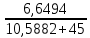 = 0,1196 А, = 0,1196 А, = = 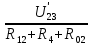 = = 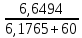 = 0,1005 А. = 0,1005 А.Решаем вторую расчетную схему (рисунок 2.16). Рассчитываем общее сопротивление для второй расчетной схемы: R13,01,6,52,5 = 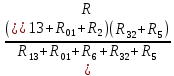 = = 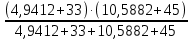 = == 22,5499 Ом, R'' = R12 + R4 + R13,01,6,32,5 = 22,5499 + 6,1765 + 60 = 88,7264 Ом. Находим общий ток для второй расчетной схемы: 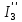 = = 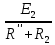 = = 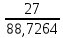 = 0,3043 (А). = 0,3043 (А). 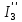 = = 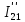 . .Р 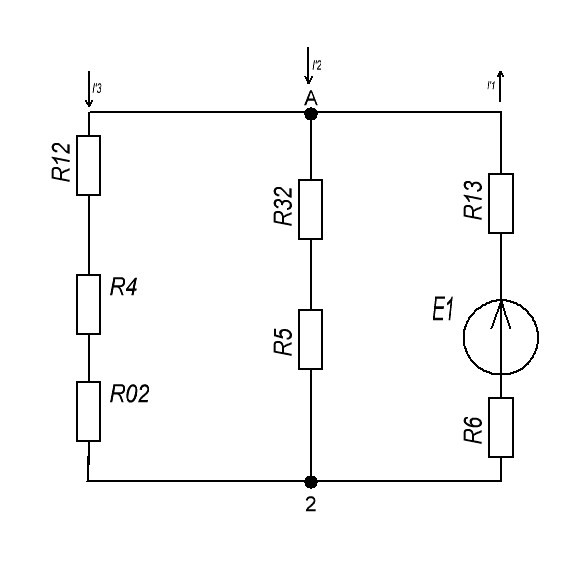 исунок 2.16 – Вторая расчетная схема Находим напряжение параллельных ветвей второй расчетной схемы: 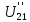 = = 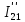 · R13,01,6,32,5 = 0,3043 ·22,5499 = 6,8619 B. · R13,01,6,32,5 = 0,3043 ·22,5499 = 6,8619 B.Определяем токи в параллельных ветвях для второй расчетной схемы: 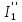 = = 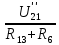 = = 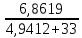 = 0,1809 А, = 0,1809 А,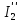 = = 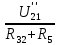 = = 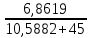 = 0,1234 А. = 0,1234 А.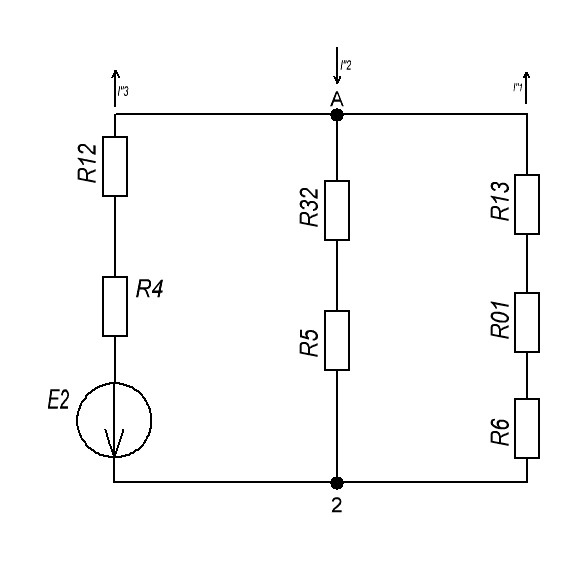 Рисунок 2.17 – Токи в каждой ветви Действительные токи находим как алгебраическую сумму частичных: I6 = 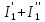 = 0,1809 + 0,2201 = 0,401 А, = 0,1809 + 0,2201 = 0,401 А,I5 = 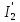 = = 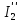 = 0,1234 = 0,1196 = 0,0038 А, = 0,1234 = 0,1196 = 0,0038 А,I4 = 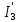 + + 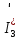 = 0,3043 + 0,1005 = 0,4048 A. = 0,3043 + 0,1005 = 0,4048 A. |
