курсач. 1курсач2 - копия (4) - копия. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
 СОДЕРЖАНИЕ Введение……………………………………………………………………3 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов .…………………………………………………………4 2 Расчет сложных электрических цепей постоянного тока………………8 2.1 Расчет электрической цепи постоянного тока методом узловых и контурных уравнений …………………………………………………………. 8 2.2 Расчет электрической цепи постоянного тока методом контурных токов ...………………………………………………………………10 2.3 Расчет электрической цепи постоянного тока методом узловых напряжений ………………………………………………………………………12 2.4 Расчет электрической цепи постоянного того методом наложения токов ...………………………………………………………………16 3 Методика расчета линейных однофазных электрических цепей переменного тока .………………………………………………………………19 4 Расчет трехфазной цепи символическим методом при соединении приемников звездой или треугольником . .. ……………………………………22 5 Расчет трехфазной цепи символическим методом при соединении приемников звездой и треугольником ……………………………………...…26 6 Расчет реальной катушки с магнитопроводом при смешанном соединении сопротивлений на схеме замещения, построение векторной диаграммы ………………………………………………………………………35 Заключение ..………………………………………………………………39 Список использованных источников ……………………………………40 ВВЕДЕНИЕ Электротехникой в широком смысле слова называется обширная область практического применения электромагнитных явлений. Широкое и разнообразное использование электрической энергии объясняется тем, что она имеет огромное преимущество перед другими формами энергии. Только на базе электричества оказалось возможным широкое развитие новейших научно-технических направлений в радиоэлектронике, в технике связи, в области компьютерных технологий. Трудно представить жизнь современного человека без использования электрической энергии. Курс Теоретических основ электротехники (ТОЭ) в обобщенной форме рассматриваются теория и методы расчета разнообразных электромагнитных явлений. Данный курс занимает основное место среди общетехнических дисциплин, определяющих теоретический уровень профессиональной подготовки инженеров-электриков, является теоретической базой для последующего изучения специальных дисциплин. Включение дисциплины ТОЭ в государственный образовательный стандарт объясняется тем, что принцип работы всех рабочих машин, используемых в области машиностроения, и построение устройств управления ими, базируется на основных фундаментальных понятиях данной дисциплины. В ходе изучения курса электротехники учащимся необходимо изучить и выработать навыки решения электрических цепей постоянного и переменного токов различными методами РАСЧЕТ ПРОСТЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА СО СМЕШАННЫМ СОЕДИНЕНИЕМ СОПРОТИВЛЕНИЙ МЕТОДОМ ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ Для схемы электрической цепи, изображенной на рисунке 1.1, определить токи в ветвях цепи методом эквивалентных преобразований, составить баланс мощностей. Таблица 1.1 – Исходные данные
Р 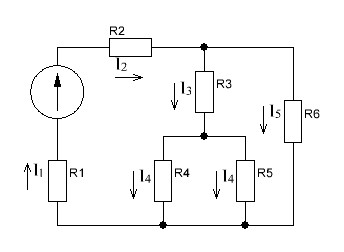 исунок 1.1 — Схема электрической цепи постоянного тока Сопротивления R4 и R5 соединены параллельно, следовательно, сопротивление R45равно: 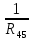 = = 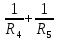 = = 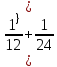 = = 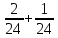 = =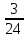 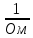 ; ;R45 = 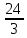 = 8 Ом. = 8 Ом.Свернем исходную схему (рисунок 1.1). Получаем схему цепи, изображенную на рисунке 1.2. В схеме цепи сопротивления R3 и R45 соединены последовательно, следовательно, сопротивление R345 можно рассчитать по формуле: R345 = R3 + R45 = 12 + 8 = 20 Ом. Р 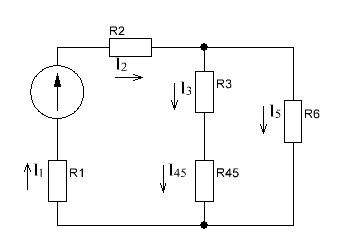 исунок 1.2 — Преобразованная схема электрической цепи постоянного тока Получаем схему цепи, изображенную на рисунке 1.3. В схеме цепи сопротивления R6 и R345 соединены параллельно: 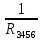 = = 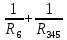 = = 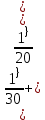 = = 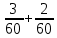 = =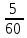 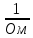 ; ;R 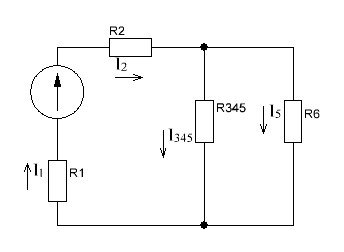 3456= 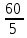 = 12 Ом. = 12 Ом.Рисунок 1.3 — Преобразованная схема электрической цепи постоянного тока Получаем схему цепи, изображенную на рисунке 1.4. В схеме цепи сопротивления R1, R2 и R3456соединены последовательно, следовательно, общее сопротивление цепи можно рассчитать по формуле: R = R1 + R2 + R3456 = 10 + 5 + 12 = 27 Ом. Р 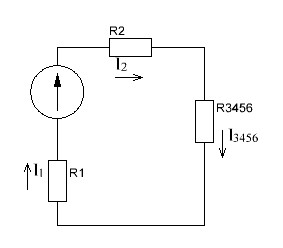 исунок 1.4 - Преобразованная схема электрической цепи постоянного тока 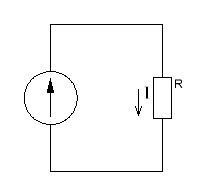 Получаем схему цепи, изображенную на рисунке 1.5. Рисунок 1.5 — Преобразованная схема электрической цепи постоянного тока Определяем токи в ветвях электрической цепи. По закону Ома для схемы цепи, изображенной на рисунке 1.5, ток I равен: I = 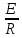 = = 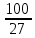 = 3,7037 А. = 3,7037 А.Разворачиваем схему, изображенную на рисунке 1.5, и переходим к схеме, приведенной на рисунке 1.4. I = I1 = I2 = I3456. Для определения токов в других ветвях цепи находим напряжения на этих ветвях. Напряжение U1 и U2 для схемы цепи, изображенной на рисунке 1.4, определим по закону Ома: U1 = I1 R1 = 3,7037 10 = 37,037 В; U2 = I2 R2 = 3,7037 5 = 18,5185 В. Напряжение U3456 для схемы цепи, изображенной на рисунке 1.4, определим по закону Ома: U3456 = I3456 R3456 = 3,7037 12 = 44,4444 В = U6 = U345 . По закону Ома в схеме цепи, приведенной на рисунке 1.3: I6 = 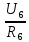 = = 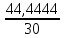 = 1,4815 А; = 1,4815 А;I345 = I3 =I45 = 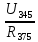 = = 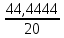 = 2,2222 А. = 2,2222 А.По закону Ома в схеме цепи, изображенной на рисунке 1.2: U45 = I45 R45 = 2,2222 8 = 17,7776 В = U4 = U5. По закону Ома в схеме цепи, приведенной на рисунке 1.1: I4 = 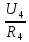 = = 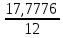 = 1,4815 А; = 1,4815 А;I5 = 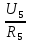 = = 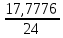 = 0,7407 А. = 0,7407 А.Составляем уравнение баланса мощностей: РИСТ = РПОТР. Мощность источника энергии равна: РИСТ = EI1 = 100 3,7037 = 370,37 Вт. Мощность приемников энергии рассчитываем по формуле: РПОТР = 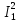 R1+ R1+ 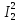 R2 + R2 + 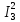 R3 + R3 + 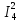 R4 + R4 + 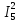 R5 + R5 + 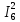 R6= R6== 3,70372 10 + 3,70372 5 + 2,22222 12 + + 1,48152 12 + 0,74072 24 + 1,48152 30 = 370,3698 Вт; 370,37 Вт = 370,3698 Вт. Баланс мощностей соблюдается, следовательно, токи определены правильно. МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Для электрической цепи, изображенной на рисунке 2.1, необходимо: определить токи во всех ветвях, используя метод узловых и контурных уравнений; рассчитать токи во всех ветвях методом контурных токов; найти токи во всех ветвях на основании метода узлового напряжения; определить токи во всех ветвях, используя метод наложения токов. Параметры элементов электрической цепи указаны в таблице 2.1. Таблица 2.1 — Исходные данные
РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА МЕТОДОМ УЗЛОВЫХ И КОНТУРНЫХ УРАВНЕНИЙ М 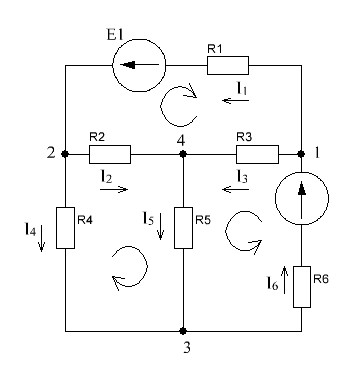 етод узловых и контурных уравнений подразумевает составление системы уравнений по первому и второму законам Кирхгофа. Он не требует никаких преобразований схемы и применяется для расчета любой электрической цепи. Рисунок 2.1 - Принципиальная схема электрической цепи постоянного тока Для схемы, изображенной на рисунке 2.1, указываем направления действительных токов в ветвях I1, I2, I3, I4, I5, I6. В заданной цепи шесть ветвей (т = 6), значит, в системе должно быть шесть уравнений. Сначала составляем уравнения по первому закону Кирхгофа. В цепи четыре узла (n = 4), следовательно, нужно составить три уравнения (n - 1 = 4 - 1 = 3). Например, для узлов 1, 2, 3 по первому закону Кирхгофа запишем уравнения: узел 1: –I1 + I6 – I3 = 0; узел 2: + I1 – I2 – I4 = 0; узел 3: I4 + I5 – I6 = 0. Составляем оставшиеся три уравнения по второму закону Кирхгофа для независимых контуров. Чтобы контур был независимым, необходимо в каждый следующий контур включить одну ветвь, не входящую в предыдущие. Выбираем направления обходов и составляем уравнения. При составлении уравнений учитываем следующее. Если направление ЭДС совпадает с направлением обхода контура, ЭДС записывается со знаком «+», если их направления противоположны, то ЭДС берем со знаком «–». Падение напряжения на резисторе записываем со знаком «+», если направления обхода контура и тока, протекающего через него, совпадают, а со знаком «–» - если их направления противоположны. Контур 1421 (обход против часовой стрелке): E1 = I2 R2 + I1 (R1 + R01) – I3 R3. Контур 2432 (обход по часовой стрелке): 0 = I2 R2 + I5 R5 – I4 R4. Контур 1431 (обход против часовой стрелки): E2 = I3 R3 + I6 (R6+ R02)+ I5 R5. Записываем уравнения для узлов и контуров в систему. Получили систему из шести уравнений с шестью неизвестными: 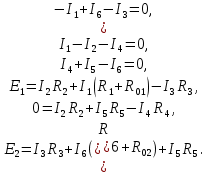 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 2.1: 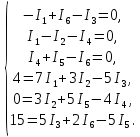 Решаем систему уравнений методом Крамера, применяя специализированные инструменты математического анализа. Заполним таблицу 2.2. Таблица 2.2 — Коэффициенты при токах из системы уравнений
|
