курсач. 1курсач2 - копия (4) - копия. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Расчет фазных и линейных токов приемника, токов в проводах сети графоаналитическим методом Фазные напряжения приемника № 4, благодаря нулевому проводу, равны: UA = UB = UC = 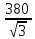 = 220 В. = 220 В.Найдем 4 : tg4 = 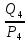 = = 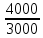 = 1,33333; = 1,33333;4 = arctg 4 = arctg1,33333 = +53,130; cos4 = cos +53,130 = 0,600001. Рассчитаем фазные токи приемника № 4: I1 = I2 = I3 = 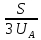 = = 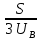 = = 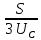 = = 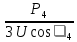 = =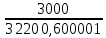 = 7,57576 A. = 7,57576 A.Согласно первому закону Кирхгофа для нулевой точки: 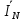 = = 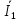 + +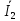 + +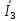 . .Следовательно, построив симметричную трехлучевую звезду фазных напряжений и отложив вдоль векторов этих напряжений фазные токи (так как 4 = =+53,130), можно определить вектор тока в нулевом проводе, геометрическисложив эти токи. Фазные напряжения приемников № 1, № 2 и № 3 равны: UAB = UBC = UCA = Uлин = 380 В. Определим sin1 и sin3, а также углы 1,2 и 3; sin1 = 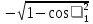 = = 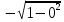 = –1; = –1;1 = arcsin1 = arcsin(–1) = –900; sin3 = 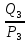 = = 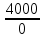 = +900; = +900;cos3 = cos +900 = 0; sin3 = 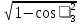 = = 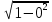 = 1; = 1;3 = arccos3 = arccos 1 = 00. Найдем фазные токи: Iab = 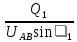 = = 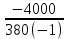 = 10,5263 A; = 10,5263 A;Ibc = 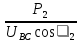 = = 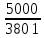 = 13,1579 A; = 13,1579 A;Ica = 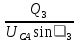 = = 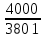 = 10,5263 A. = 10,5263 A.Выбираем масштаб напряжений и токов: M (U) = 55 В/см, М (I) = 3 А/см. Рассчитаем длины векторов напряжений: l(UA) = 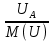 = = 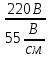 = 4,0 см, = 00; = 4,0 см, = 00;l(UB) = 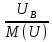 = = 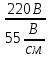 = 4,0 см, = –1200; = 4,0 см, = –1200;l(UC) = 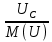 = = 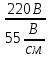 = 4,0 см, = +1200; = 4,0 см, = +1200;l(UAB) = 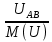 = = 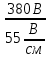 = 6,9 см, = +300; = 6,9 см, = +300;l(UBC) = 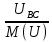 = = 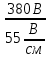 = 6,9 см, = – 900; = 6,9 см, = – 900;l(UCA) = 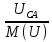 = = 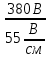 = 6,9 см, = +1500. = 6,9 см, = +1500.Рассчитаем длины векторов токов: l(Iab) = 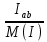 = = 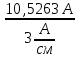 = 3,5 см, 1 = –90 0; = 3,5 см, 1 = –90 0;l(Ibc) = 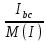 = = 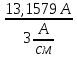 = 4,4 см, 2 = 00; = 4,4 см, 2 = 00;l(Ica) = 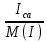 = = 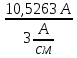 = 3,5 см, 3 = +900; = 3,5 см, 3 = +900;l(I1) = l(I2) = l(I3) = 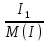 = = 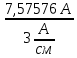 = 2,5 см, 4 = +53 0; = 2,5 см, 4 = +53 0;l(IN) = 0 см; 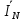 = l(IN) = l(IN) М (I)= 3 М (I)= 3  0 = 0 А; 0 = 0 А;l(Ia) = 3,3 см, 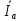 = = 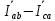 = l(Ia) = l(Ia) М (I)= 3 М (I)= 3  3,3 = 9,9 А; 3,3 = 9,9 А;l(Ib) = 7,6 см, 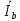 = = 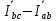 = l(Ib) = l(Ib) М (I)= 3 М (I)= 3  7,6 = 22,8 А; 7,6 = 22,8 А;l(Ic) = 7,6 см, 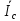 = = 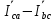 = l(Ic) = l(Ic) М (I)= 3 М (I)= 3  7,6 = 22,8 А; 7,6 = 22,8 А;l(IA) = 2,6 см, 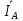 = l(IA) = l(IA) М (I)= 3 М (I)= 3  3,6 = 7,8 А; 3,6 = 7,8 А;l(IB) = 7,8 см, 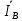 = l(IB) = l(IB) М (I)= 3 М (I)= 3  7,8 = 23,4 А; 7,8 = 23,4 А;l(IC) = 9,1 см, 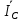 = l(IC) = l(IC) М (I)= 3 М (I)= 3  1,9 = 27,3 А. 1,9 = 27,3 А.Полная векторная диаграмма приведена на рисунке 5.2.  Рисунок 5.2  Векторная диаграмма Векторная диаграммаРАСЧЕТ РЕАЛЬНОЙ КАТУШКИ С МАГНИТОПРОВОДОМ ПРИ СМЕШАННОМ СОЕДИНЕНИИ СОПРОТИВЛЕНИЙ НА СХЕМЕ ЗАМЕЩЕНИЯ, ПОСТРОЕНИЕ ВЕКТОРНОЙ ДИАГРАММЫ Для катушки со стальным сердечником, схема замещения которой предоставлена на рисунке 6.1, необходимо определить величину тока в катушке, подводимое переменное напряжение, мощность потерь в обмотке катушки и в стальном сердечнике, построить векторную диаграмму катушки. Параметры схемы замещения катушки: R 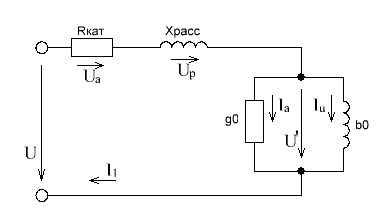 кат = 1,5 Ом; Xрасс = 2 Ом; b0 = 0,072 См; g0 = 0,009 См; U' = 95 В. Рисунок 6.1 – Схема замещения катушки со стальным сердечником Расчет реальной катушки с магнитопроводом, построение векторной диаграммы Определим активные и реактивные составляющие тока. Активная составляющая тока: Ia = U' g0 = 100 0,009 = 0,9 А. Реактивная составляющая тока: Iμ = U' b0 = 100 0,072 = 7,2 А. Рассчитаем величину тока в обмотке: I = 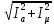 = = 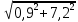 = 7,2560 А. = 7,2560 А.Определим параметры неразветвленной схемы замещения катушки: эквивалентное сопротивление R0, вызывающее потери, равные потерям в стали: R0 = 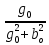 = = 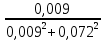 = 1,7094 Ом; = 1,7094 Ом;индуктивное сопротивление: X0 = 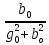 = = 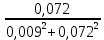 = 13,675 Ом. = 13,675 Ом.Напряжение, подводимое к входным зажимам катушки, рассчитаем по формуле: U = IZ = I 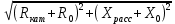 = == 7,256 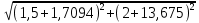 = 116,1 В. = 116,1 В.Для построения векторной диаграммы определим падения напряжения на сопротивлениях Rкат и Xрасс: Ua = IRкат = 7,256 1,5 = 10,884 В; Uр = IXрасс = 7,256 2 = 14,512 В. Угол потерь δ: δ = arctg 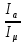 = arctg = arctg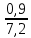 = 7,130. = 7,130.Мощность потерь в обмотке катушки: Рмеди = I2 Rкат = 7,2562 1,5 = 78,97 Вт. Мощность потерь в стальном сердечнике: Рстали = I2 R0 = 7,2562 1,7094 = 90 Вт. Общая мощность потерь в катушке: Р = Рстали + Рмеди = 78,97 + 90 = 168,97 (Вт). Коэффициент мощности: cos = 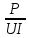 = =  = 0,2005765, = 0,2005765,где = 78,43° — угол сдвига фаз между векторами напряжения 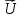 и тока и тока 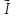 . .Построение векторной диаграммы для катушки с магнитопроводом Выбираем масштабы тока М(I) = 1,2 А/см, напряжения М(U) = 10 В/см. Рассчитываем длины векторов: l(Iа) = 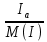 = = 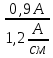 = 0,8 см; = 0,8 см;l(Iμ) = 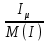 = = 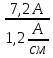 = 6 см; = 6 см;l(U) = 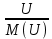 = = 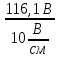 = 11,6 см; = 11,6 см;l(U') = 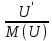 = = 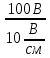 = 10 см; = 10 см;l(Ua) = 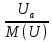 = = 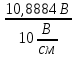 = 1,1 см; = 1,1 см;l(Up) = 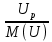 = = 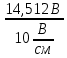 = 1,5 см. = 1,5 см.В масштабе строим полную векторную диаграмму катушки со стальным сердечником (рисунок 6.2). При построении векторной диаграммы учитываем, что вектор 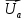 и и 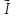 совпадают по фазе, т. е. параллельны друг другу; вектор напряжения совпадают по фазе, т. е. параллельны друг другу; вектор напряжения 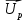 опережает вектор тока опережает вектор тока 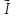 , а следовательно, и вектор напряжения , а следовательно, и вектор напряжения  по фазе на угол π/2. по фазе на угол π/2. Рисунок 6.2  Векторная диаграмма Векторная диаграммаЗАКЛЮЧЕНИЕ В ходе написания данного курсового проекта я закрепил знания и навыки, полученные в ходе изучения курса теоретических основ электротехники. Мною были освоены навыки расчёта электрических цепей постоянного и переменного токов различными способами. А именно: решение задач переменного тока следующими способами: методом проводимостей и символическим; решение задач постоянного тока следующими способами: методом узловых и контурных напряжений, методом контурных токов, методом узлового напряжения и методом наложения токов; решение трёхфазных цепей переменного тока символическим и графоаналитическим методами; расчёт реальной катушки индуктивности с магнитопроводом при смешанном соединении. Также был закреплен навык построения диаграмм трехфазных цепей переменного тока соединенных звездой и треугольником. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Теоретические основы электротехники / Лоторейчук Е.А. − ИД “ФОРУМ”: ИНФРА − М, 2008. − 320 с. Теоретические основы электротехники: учеб. Пособие / А. В. Крутов, Э. Л. Кочетова, Т. Ф. Гузанова. − Минск РИПО, 2014. − 375 с. Теоретические основы электротехники. Курсовая работа: учебное пособие / Е.С.Гутько, Т.С.Шмакова. − Минск: РИПО, 2020. − 151 с. Байдук О.В. Методические рекомендации по оформлению курсовых проектов (работ) / О.В. Байдук, О.В. Липко, М.О. Лебедь, Г.Б. Румак: УО “Брестский государственный колледж связи”, 2020. − 22 с. |
