курсач. 1курсач2 - копия (4) - копия. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА МЕТОДОМ КОНТУРНЫХ ТОКОВ Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе. Достигается это разделением схемы на независимые контуры и введением для каждого контура своего контурного тока, являющегося расчетной величиной. При решении задачи данным методом можно использовать следующий алгоритм. Определить независимые контуры и выбрать в них направления контурных токов. Составить систему уравнений (количество уравнений равно количеству независимых контуров). Р 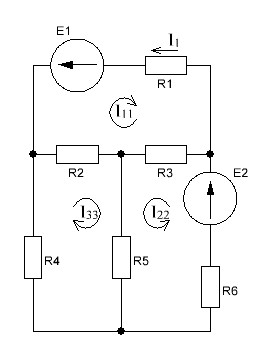 ешив систему, найти контурные токи. На основании приведенного алгоритма расчитываем схему, изображенную на рисунке 2.2. Рисунок 2.2 - Принципиальная схема электрической цепи постоянного тока Число уравнений в системе должно быть равно числу независимых контуров. В заданной цепи рассмотрим три независимых контура (1421, 2342, 1431) и введем для них контурные токи I11, I22, I33. Стрелками указываем выбранные направления контурных токов. Составляем уравнения для каждого контура. Контур 1421: E1= R1 · I11 + R2 ·(I11 + I33) +R3 · (I11 - I22). Контур 2342: 0 = R4 · I33 + R2 ·(I11 + I33) +R5 · (I22+I33). Контур 1431: E2 = R · I22 +R5 · (I22+I33)+ R3 ·(I22 – I11). Составляем систему уравнений: 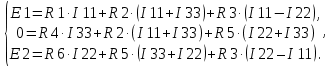 Подставляем в уравнения численные значения ЭДС и сопротивлений из таблицы 2.1: 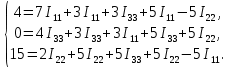 Упростим и запишем данную систему так, чтобы контурные токи во всех уравнениях располагались по порядку: 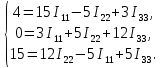 Вычислим контурные токи: I11 = 1,3048 А; I22 = 2,3349 А; I33 = -1,2991 А. РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА МЕТОДОМ УЗЛОВОГО НАПРЯЖЕНИЯ Приведем схему, изображенную на рисунке 2.3, к двум узлам, преобразовывая треугольник сопротивлений R1, R4, R6 в эквивалентную звезду сопротивлений R14, R46, R16. Новый узел обозначим А (рисунки 2.4, 2.5, 2.6). Р 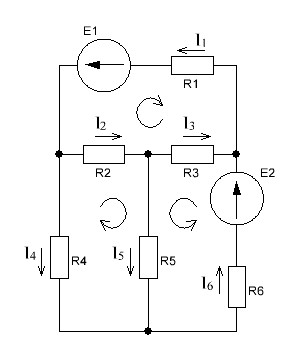 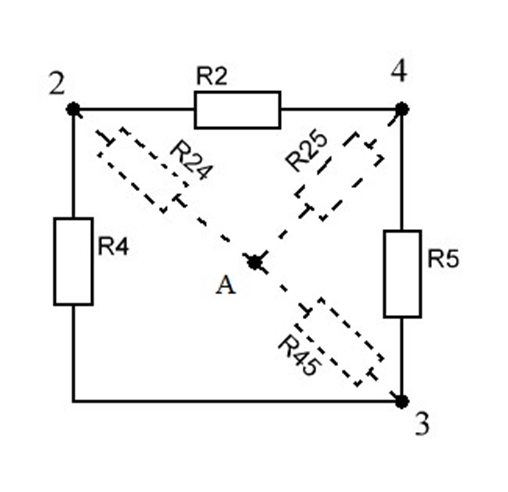 исунок 2.3 - Принципиальная схема электрической цепи постоянного тока Р 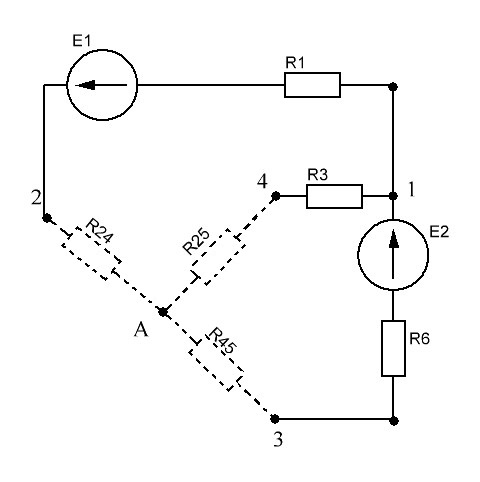 исунок 2.4 – Преобразование треугольника сопротивлений в звезду Рисунок 2.5 – Схема, преобразованная к двум узлам Рассчитаем величины сопротивлений эквивалентной звезды: R24 = 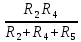 = = 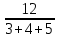 = = 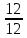 = 1 Ом; = 1 Ом;R16 = 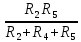 = = 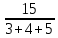 = = 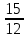 = 1,25 Ом; = 1,25 Ом;R 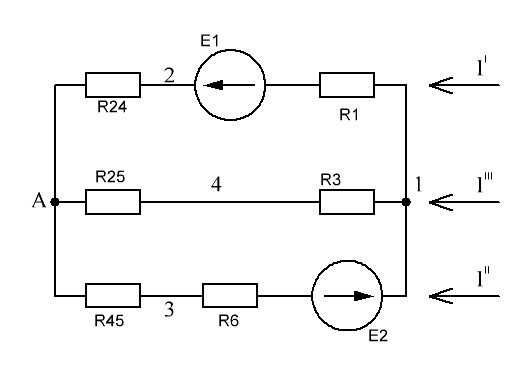 45 = 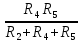 = = 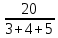 = = 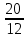 = 1,6667 Ом. = 1,6667 Ом.Рисунок 2.6 – Схема, преобразованная к двум узлам Выбираем направление токов в параллельных ветвях влево: I', I", I"'. Определим общее сопротивление каждой ветви: R' = R1+ R01 + R24 = 7 + 0 + 1 = 8 Ом; R" = R6+ R02 + R45 = 2 + 0 + 1,6667 = 3,6667 Ом; R'" = R3 + R25 = 5 + 1,25 = 6,25 Ом. Рассчитаем проводимость каждой ветви: g' = 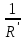 = = 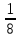 = 0,125 См; = 0,125 См;g'' = 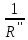 = = 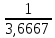 = 0,2727248 См; = 0,2727248 См;g''' = 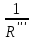 = = 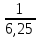 = 0,16 См. = 0,16 См.Определим узловое напряжение: UА1 = 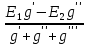 = = 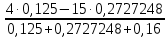 = = 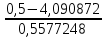 = – 6,438430 В. = – 6,438430 В.Находим токи в каждой ветви: I' =(E1 – UА1)·g' = (4 + 6,438430) · 0,125 = 10,43843 · 0,125 = 1,3048 А; I'' =(-E2 – UА1)·g''= (-15 + 6,438430) · 0,2727248 = −8,56157 · 0,2727248= = −2,3349 А; I''' =(– UА1)·g'''= 6,438430 · 0,16 = 1,0301 А. Действительные токи равны: I1 = I' = 1,3048 А - влево; I5 = I" = −2,3349 А - вправо; I3 = I''' = 1,0301 А - влево. 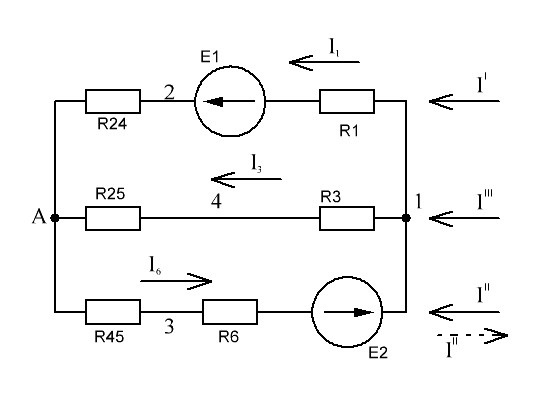 Рисунок 2.7 – Токи в каждой ветви В 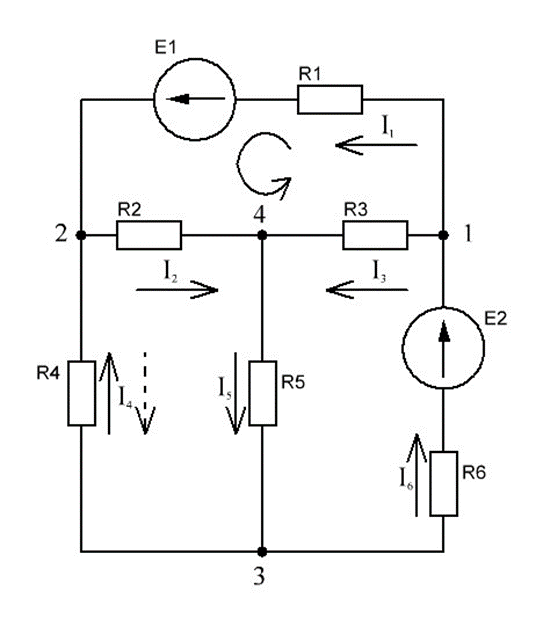 ернемся к исходной схеме. Выберем I6 вниз, I1и I3 влево. Рисунок 2.8 – Принципиальная схема электрической цепи постоянного тока Для контура 2412 составляем уравнение по второму закону Кирхгофа (обход против часовой стрелки): E1 = I1 (R1 + R01) + I2 R2 – I3 R3. Выражаем из него ток I2: I2 = 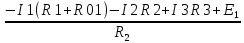 = = 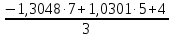 = 0,0056 А - вправо. = 0,0056 А - вправо.По первому закону Кирхгофа находим токи I4и I5: узел 4: I2 +I3 – I5 = 0; I5 = I2 + I3 = 0,0056 + 1,0301 = 1,0357 А - вниз; узел 2: I4 + I1 – I2 = 0; I4 = – I1 + I2= – 1,3048 +0,0056 = – 1,2992 А - вниз. В результате действительные токи равны: I1 = 1,3048 А; I2 = 0,0056 А; I3 = 1,0301 А; I4 = 1,2992 А; I5 = 1,0357 А; I6 = 2,3349 А. РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА МЕТОДОМ НАЛОЖЕНИЯ ТОКОВ Приведем исходную схему (рисунок 2.1) к двум узлам (рисунок 2.9), преобразовывая треугольник сопротивлений R1, R4, R6 в эквивалентную звезду сопротивлений R23, R53, R23. Сопротивления эквивалентной звезды рассчитаны ранее: R23 = 11,4286 Ом; R25 = 7,7922 Ом; R53 = 4,2857 Ом. Для схемы электрической цепи, изображенной на рисунке 2.9, составляем расчетные схемы (рисунки 2.10, 2.11). Указываем на них направления частичных токов. Р 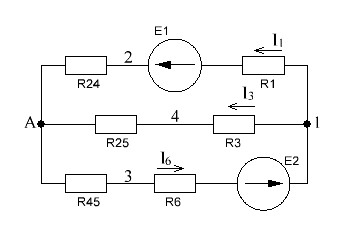 исунок 2.9 — Схема электрической цепи, приведенная к двум узлам Р 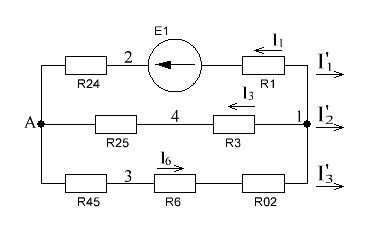 ешаем первую расчетную схему (рисунок 2.10) методом эквивалентных преобразований (методом «свертывания»). Рисунок 2.10 — Первая расчетная схема Находим общее сопротивление для первой расчетной схемы: R45,6,25,02,3 = 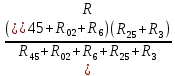 = = 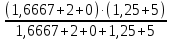 = = 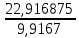 = == 2,3109 Ом; R' = R1 +R24 + R45,6,25,02,3 = 7 + 1 + 2,3109 = 10,3109 Ом. Находим общий ток для первой расчетной схемы: 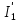 = = 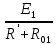 = = 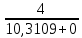 = 0,3879 А. = 0,3879 А. 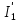 = = 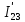 . .Рассчитываем напряжение параллельных ветвей: 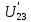 = = 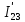 ·R45,6,25,02,3= 0,3879·2,3109 = 0,8964 В. ·R45,6,25,02,3= 0,3879·2,3109 = 0,8964 В.Определяем частичные токи на параллельных ветвях для первой расчетной схемы: 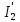 = = 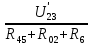 = = 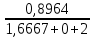 = 0,2445 А; = 0,2445 А;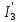 = = 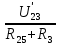 = = 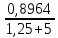 = 0,1434 А. = 0,1434 А.Решаем вторую расчетную схему (рисунок 2.11). Рассчитываем общее сопротивление для второй расчетной схемы: R24,01,1,25,3 = 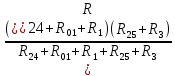 = = 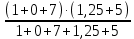 = = 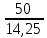 = == 3,5088 Ом; R'' = R6+R45 + R24,01,1,25,3= 1,6667 + 2 + 3,5088 = 7,1755 Ом. Находим общий ток для второй расчетной схемы: 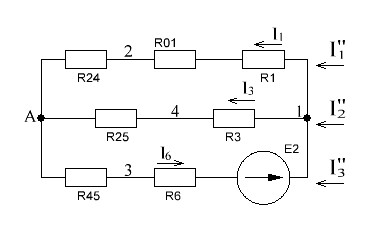 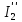 = = 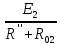 = = 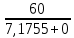 = 2,0904 А. = 2,0904 А. 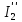 = = 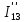 . .Рисунок 2.11 — Вторая расчетная схема Действительные токи находим как алгебраическую сумму частичных: I6 = 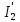 + + 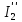 = 2,0904 + 0,2445 = 2,3349 А – вправо. = 2,0904 + 0,2445 = 2,3349 А – вправо.МЕТОДИКА РАСЧЕТА ЛИНЕЙНЫХ ОДНОФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И 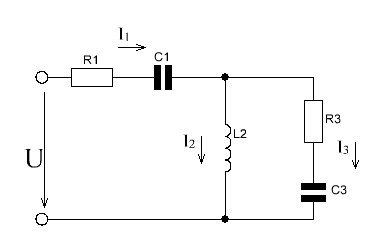 сходные данные для выполнения расчета: X1 = 795,8 мкФ; L2 = 15,19 мГн; R3 = 6 Ом; С3 = 397,9 мкФ; U = 20 В. Рисунок 3.1 - Схема для расчета однофазной электрической цепи переменного тока Расчет линейной однофазной электрической цепи переменного тока методом проводимостей Рассчитаем сопротивления: 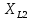 = = 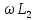 = 50 · 3,1416 · 50 · 15,92 · 10-3 5 Ом; = 50 · 3,1416 · 50 · 15,92 · 10-3 5 Ом;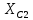 = = 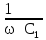 = = 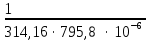 4 Ом; 4 Ом;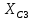 = = 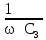 = = 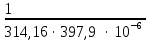 8 Ом; 8 Ом;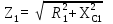 = =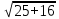 = = 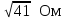 ; ;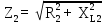 = = 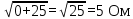 ; ;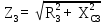 = = 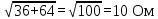 . .Рассчитаем проводимости на параллельном участке цепи. Активные проводимости: 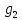 = = 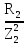 = = 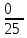 = 0 Cм; = 0 Cм;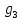 = = 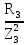 = = 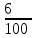 = 0,06 Cм. = 0,06 Cм.Реактивные проводимости: 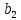 = = 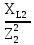 = = 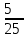 = 0,2 См; = 0,2 См;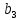 = = 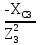 = = 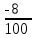 = - 0,08 См. = - 0,08 См.Полную проводимость на участке 23 определим по формуле y23 = 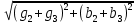 = = 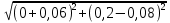 = == 0,134164 См. Полная проводимость ветви 23: у2 = 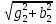 = = 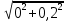 = 0,2 См. = 0,2 См.Полная проводимость ветви 253: у3 = 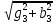 = = 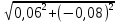 = 0,1 См. = 0,1 См.Рассчитаем полное сопротивление участка 23: Z23 = 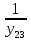 = = 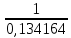 = 7,45356 Ом. = 7,45356 Ом.Определим активное и реактивное сопротивления параллельного участка 23: R23 = 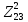 · g23= 7,453562· 0,06 = 3,33333 Ом; · g23= 7,453562· 0,06 = 3,33333 Ом;X23 = 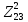 · b23= 7,453562· (0,2 – 0,08) = 6,66667 Ом. · b23= 7,453562· (0,2 – 0,08) = 6,66667 Ом.Сопротивление Х23 - положительное, т. е. является индуктивным. Теперь в схеме все сопротивления включены последовательно и поэтому полное сопротивление всей цепи: Z = 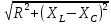 = = 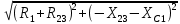 = = = 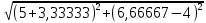 = 8,47960 Ом. = 8,47960 Ом.Ток в цепи определяем по закону Ома: I = I1 = 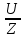 = = 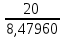 = 2,28582 А. = 2,28582 А.Для того чтобы найти токи I2, I3, определим напряжение на этом участке: U23= I1·Z23= 2,28582·7,45356 = 17,0375 В. Токи I2, I3 находим по закону Ома: I1 = U23· y2 = 17,0375·0,2 = 3,4075 A; I1 = U23· y2 = 17,0375·0,1 = 1,70375 A. |
