курсач. 1курсач2 - копия (4) - копия. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ СИМВОЛИЧЕСКИМ МЕТОДОМ ПРИ СОЕДИНЕНИИ ПРИЕМНИКОВ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ В четырехпроводную трехфазную сеть включены два приемника, один из которых соединен звездой, другой - треугольником (№ 1, № 2, № 3 - несимметричный, № 4 - симметричный). Для данных, приведенных в таблице 5.1, необходимо: Рассчитать сопротивления элементов схемы замещения приемников; Начертить схему включения приемников к трехфазной сети; Определить фазные и линейные токи приемника, токи в проводах сети; Построить векторную диаграмму напряжений, совмещенную с векторной диаграммой токов. Таблица 5.1  Исходные данные Исходные данные
Линейное напряжение сети Uлин = 380 В. Расчет сопротивления элементов схемы замещения приемников Выполним расчет сопротивлений элементов схемы замещения приемников: № 1: Найдем sin1. Берем со знаком «  », т.к. характер нагрузки емкостной. », т.к. характер нагрузки емкостной.sin1 = 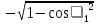 = = 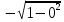 = =  1; 1;Z1 = 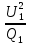 · sin1 = · sin1 =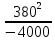 · (-1) = 36,1 Ом; · (-1) = 36,1 Ом;R1 = Z1 · cos1= 36,1 · 0 = 0 Ом; X1 = Z1 · sin1 = 36,1 · (-1) = -36,1 Ом; 1 = arccos 0 = arcsin(  1) = 1) =  900; 900;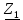 = R1 + j · X1 = Z1 · = R1 + j · X1 = Z1 · 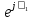 = 0 - j · 36,1 = 44· = 0 - j · 36,1 = 44·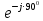 Ом. Ом.№ 2: По условию задачи cos 2 = 1. Следовательно, 2 =0°, sin 2= = sin 00 =1. Z2 = 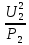 · cos2 = · cos2 =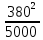 · 1 = 28,88 Ом; · 1 = 28,88 Ом;R2 = Z2 · cos2= 22,88 · 1 = 22,88 Ом; X2 = Z2 · sin2 = 22,88 · 0 = 0 Ом; 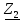 = R2 + j · X2 = Z2 · = R2 + j · X2 = Z2 · 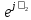 = 22,88 + j · 0 = 22,88· = 22,88 + j · 0 = 22,88·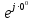 Ом. Ом.№ 3: По условию задачи P3 = 0, следовательно, приемник чисто реактивный. Тогда 2 = +900, т.к. приемник индуктивный; cos2 = cos(+900) = = 0; sin2 = sin(+900) =1. Z3 = 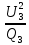 · sin3 = · sin3 =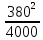 · 1 = 36,1 Ом; · 1 = 36,1 Ом;R3 = Z3 · cos3= 36,1 · 0 = 0 Ом; X3 = Z3 · sin3 = 36,1 · 1 = 36,1 Ом; 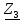 = R3 + j · X3 = Z3 · = R3 + j · X3 = Z3 · 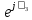 = 0 + j · 36,1 = 36,1· = 0 + j · 36,1 = 36,1·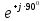 Ом. Ом.№ 4: По условию задачи P4 = 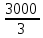 = 1000 Вт – мощность, потребляемая каждым из трех одинаковых приемников №4. = 1000 Вт – мощность, потребляемая каждым из трех одинаковых приемников №4.Найдем cos4 и sin4 через tg4: tg4= 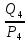 = =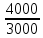 = 1,33333, 4= arctg(1,33333)=+53,130 ; = 1,33333, 4= arctg(1,33333)=+53,130 ;cos4 = cos(+53,130)=0,600001, sin4 = sin(+53,130)=0,799999; Z4 = 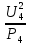 · cos4 = · cos4 =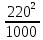 · 0,600001 = 29,0400 Ом; · 0,600001 = 29,0400 Ом;R4 = Z4 · cos4= 29,04 · 0,600001 = 17,4240 Ом; X4 = Z4 · sin4 = 29,04 · 0,799999 = 23,2320 Ом; 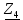 = R4 + j · X4 = Z4 · = R4 + j · X4 = Z4 · 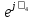 = 17,424 + j · 23,232 = 29,04· = 17,424 + j · 23,232 = 29,04·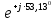 Ом. Ом.Схема включения приемников определяется в зависимости от их номинального напряжения Uном и линейного напряжения трехфазной сети Uлин. Если Uном = Uлин, то используется соединение треугольником. Если Uлин = 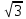 · Uном - звездой. · Uном - звездой. Таким образом, приемники № 1, № 2 и № 3 необходимо соединить треугольником, так как по условию задачи 380 В = 380 В. По условию приемники № 1, № 2 и № 3 несимметричны. Трехфазный симметричный приемник № 4 необходимо соединить звездой, так как Uлин = 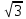 · Uном, 380 В= · Uном, 380 В= 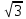 · 220 В, следовательно, необходим нулевой провод, который обеспечивает равенство по величине фазных · 220 В, следовательно, необходим нулевой провод, который обеспечивает равенство по величине фазных напряжений приемников. Схема включения приемников к трехфазной цепи приведена на рисунке 5.1. Расчет фазных и линейных токов приемника, токов в проводах сети Для определения фазных и линейных токов приемников запишем комплексные значения фазных напряжений сети, совместив вектор 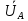 с осью действительных величин: с осью действительных величин: 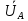 = 220 · = 220 · 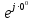 В; В;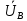 = 220 · = 220 · 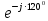 В; В;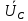 = 220 · = 220 · 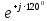 В. В.Р 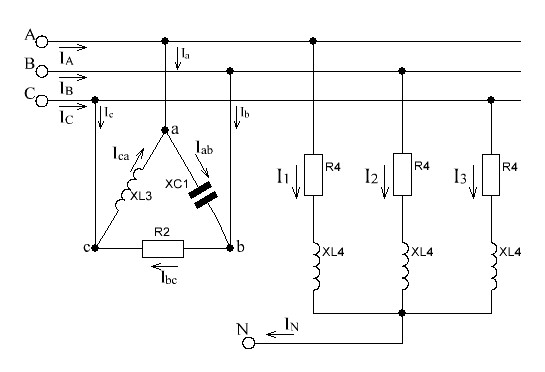 исунок 5.1 — Схема включения приемников к трехфазной цепи Линейные напряжения сети (они же и фазные напряжения приемников, соединенных треугольником) равны: 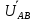 = 380 · = 380 · 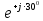 В; В;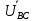 = 380 · = 380 · 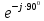 В; В;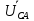 = 380 · = 380 · 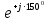 В. В.Фазные токи (они же линейные токи) приемников № 4 равны: 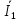 = = 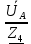 = = 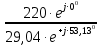 = 7,57576 · = 7,57576 ·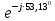 = 4,54547 - j · 6,06060 A; = 4,54547 - j · 6,06060 A;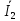 = = 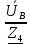 = = 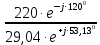 = 7,57576 · = 7,57576 ·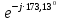 = −7,52137 – j · 0,06190 A; = −7,52137 – j · 0,06190 A;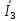 = = 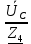 = = 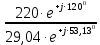 = 7,57576 · = 7,57576 ·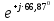 = 2,97590 + j · 6,96679 A. = 2,97590 + j · 6,96679 A.Ток в нулевом проводе: 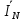 = = 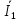 + + 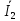 + + 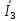 = 4,54547 − j · 6,0606 – 7,52137 – j · 0,090619 + 2,9759 + = 4,54547 − j · 6,0606 – 7,52137 – j · 0,090619 + 2,9759 ++ j · 6,96679 = 0 + j · 0 = 0 · 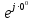 A. A.Определим фазные токи приемников №1, №2, №3: 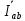 = = 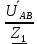 = = 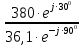 = 10,5263 · = 10,5263 ·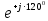 = −5,26315 + j · 9,11604 A; = −5,26315 + j · 9,11604 A;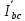 = = 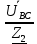 = = 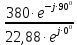 = 13,1579 · = 13,1579 ·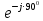 = 0 – j · 13,1579 A; = 0 – j · 13,1579 A;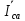 = = 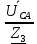 = = 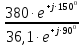 = 10,5263 · = 10,5263 ·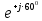 = 5,26315 + j · 9,11604 A. = 5,26315 + j · 9,11604 A.Рассчитаем линейные токи приемников №1, №2, №3: 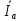 = = 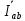 - - 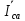 = −5,26315 + j · 9,11604 – (5,26315 + j · 9,11604) = = −5,26315 + j · 9,11604 – (5,26315 + j · 9,11604) == − 10,5263 + j · 0 = 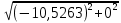 · ·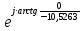 = == 10,5263 · 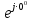 A; A;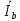 = = 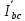 - - 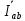 = 0 – j · 13,1579 – (−5,26315 + j · 9,11604) = = 0 – j · 13,1579 – (−5,26315 + j · 9,11604) == 5,26315 – j · 22,27394 = 22,8873 · 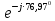 A; A;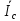 = = 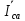 - - 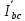 = 5,26315 + j · 9,11604 – (0 – j · 13,1579) = = 5,26315 + j · 9,11604 – (0 – j · 13,1579) == 5,26315 + j · 22,27394 = 22,8873 · 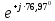 A. A.Токи в линейных проводах определяем по первому закону Кирхгофа: 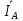 = = 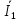 + + 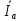 = 4,54547 - j · 6,06060 − 10,5263 + j · 0 = = 4,54547 - j · 6,06060 − 10,5263 + j · 0 == −5,98083 – j · 6,0606 = 8,51476 · 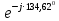 A; A;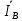 = = 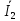 + + 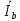 = −7,52137 – j · 0,06190 + 5,26315 – j · 22,27394 = = −7,52137 – j · 0,06190 + 5,26315 – j · 22,27394 == −2,25822 – j · 23,18013 = 23,2899 · 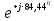 A; A;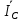 = = 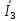 + + 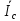 = 2,97590 + j · 6,96679 + 5,26315 + j · 22,27394 = = 2,97590 + j · 6,96679 + 5,26315 + j · 22,27394 == 8,23905 + j · 29,24073 = 30,3793 · 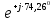 A. A.Построение векторной диаграммы напряжений, совмещенной с векторной диаграммой токов Для построения векторной диаграммы напряжений векторы фазных, а затем линейных напряжений размещают на комплексной плоскости. Для построения векторной диаграммы выбираем масштаб напряжений и токов: M (U) = 55 В/см, М (I) = 5 А/см. Рассчитаем длины векторов напряжений: l(UA) = 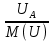 = = 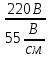 = 4,0 см, = 00; = 4,0 см, = 00;l(UB) = 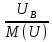 = = 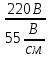 = 4,0 см, = –1200; = 4,0 см, = –1200;l(UC) = 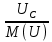 = = 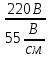 = 4,0 см, = +1200; = 4,0 см, = +1200;l(UAB) = 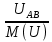 = = 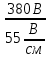 = 6,9 см, = +300; = 6,9 см, = +300;l(UBC) = 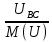 = = 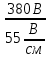 = 6,9 см, = – 900; = 6,9 см, = – 900;l(UCA) = 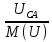 = = 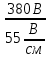 = 6,9 см, = +1500. = 6,9 см, = +1500.Рассчитаем длины векторов токов симметричного приемника: l(I1) = 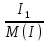 = = 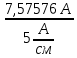 = 1,5 см, = – 530; = 1,5 см, = – 530;l(I2) = 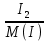 = = 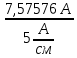 = 1,5 см, = – 1730; = 1,5 см, = – 1730;l(I3) = 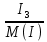 = = 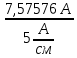 = 1,5 см, = +670. = 1,5 см, = +670.Ток в нейтральном проводе будет равен 0: l(IN) = 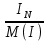 = = 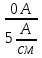 = 0 см, = 0,0; = 0 см, = 0,0;Рассчитаем длины векторов токов приемников №1, №2, №3: l(Iab) = 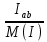 = = 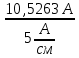 = 2,1 см, = + 1200; = 2,1 см, = + 1200;l(Ibc) = 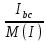 = = 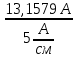 = 2,6 см, = – 900; = 2,6 см, = – 900;l(Ica) = 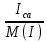 = = 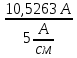 = 2,1 см, = + 600. = 2,1 см, = + 600.Линейные токи приемников №1, №2, №3 определяем разностью фазных токов: 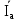 = = 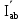 - - 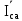 ; ;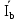 = = 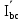 - - 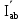 ; ;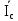 = = 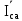 - - 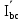 . .При этом построенные векторы токов 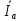 , , 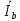 , , 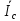 должны совпасть с расчетными значениями: должны совпасть с расчетными значениями:l(Ia) = 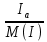 = = 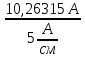 = 2,1 см, = 00; = 2,1 см, = 00;l(Ib) = 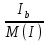 = = 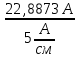 = 4,6 см, = – 770; = 4,6 см, = – 770;l(Ic) = 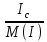 = = 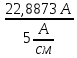 = 4,6 см, = +770; = 4,6 см, = +770; |
