курсач. 1курсач2 - копия (4) - копия. 1 Расчет простых электрических цепей постоянного тока со смешанным соединением элементов
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Расчет линейной однофазной электрической цепи переменного тока символическим методом Начертим схему замещения однофазной цепи переменного тока (рисунок 3.2). Р 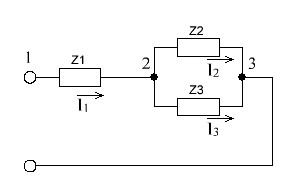 исунок 3.2 - Схема замещения однофазной цепи переменного тока Комплексы сопротивлений участков (по номерам токов) и полного сопротивления цепи будут равны: 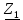 =R1 – j =R1 – j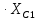 = 5 – j·4 = = 5 – j·4 = 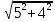 · · = 6,40312· = 6,40312·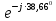 Ом; Ом;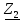 =+ j =+ j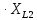 = + j·5 = 5· = + j·5 = 5·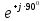 Ом; Ом;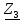 =R3 – j =R3 – j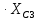 =6 – j·8 = 10· =6 – j·8 = 10·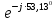 Ом. Ом.Комплекс сопротивления участка 23 цепи: 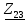 = =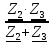 = =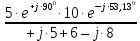 = = 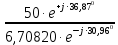 = == 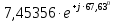 =2,81265 + j·6,90251 Ом. =2,81265 + j·6,90251 Ом.РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА ПРИ СОЕДИНЕНИИ ФАЗ ПРИЕМНИКА ЗВЕЗДОЙ ИЛИ ТРЕУГОЛЬНИКОМ Для данных, приведенных в таблице 4.1, необходимо: Рассчитать сопротивления элементов схемы замещения приемников; Начертить схему включения приемников в трехфазную сеть; Определить фазные токи каждого приемника и ток в нулевом проводе; Рассчитать мощности; Построить векторную диаграмму. Таблица 4.1 — Исходные данные
Линейное напряжение сети Uлин = 220 В. Расчет сопротивления элементов схемы замещения приемников Выполним расчет сопротивлений элементов схемы замещения приемников: № 1: Найдем sin1. Берем со знаком «  », т.к. характер нагрузки емкостной. », т.к. характер нагрузки емкостной.sin1 = 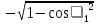 = = 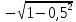 = =  0,866025; 0,866025;Z1 = 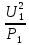 · cos 1 = · cos 1 =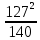 · 0,5 = 57,6036 Ом; · 0,5 = 57,6036 Ом;R1 = Z1 · cos1= 57,6036 · 0,5 = 28,8018 Ом; X1 = Z1 · sin1 = 57,6036 · (  0,866025) = 0,866025) = 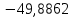 Ом; Ом;1 = arccos 0,5 = arcsin(  0,866025) = 0,866025) =  600; 600;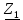 = R1 + j · X1 = Z1 · = R1 + j · X1 = Z1 · 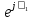 = 28,8018 = 28,8018  j · 49,8862 = 57,6036· j · 49,8862 = 57,6036·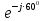 Ом. Ом.№ 2: По условию задачи cos 2 = 0. Следовательно, 2 = +90° (характер нагрузки чисто индуктивный), sin 3 = sin 900 = 1. Z2 = 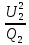 · sin 2 = · sin 2 =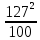 · 1 = 161,29 Ом; · 1 = 161,29 Ом;R2 = Z2 · cos2= 161,29 · 0 = 0 Ом; X2 = Z2 · sin2 = 161,29 · 1 = 161,29 Ом; 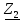 = R2 + j · X2 = Z2 · = R2 + j · X2 = Z2 · 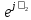 = 0 + j · 161,29 = 161,29· = 0 + j · 161,29 = 161,29·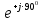 Ом. Ом.№ 3: По условию задачи cos 3 = 1. Следовательно, 3 = 0°, sin 3 = = sin 00 = 0. Z3 = 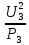 · cos3 = · cos3 =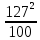 · 1 = 161,29 Ом; · 1 = 161,29 Ом;R3 = Z3 · cos3= 161,29 · 1 = 161,29 Ом; X3 = Z3 · sin3 = 161,29 · 0 = 0 Ом; 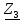 = R3 + j · X3 = Z3 · = R3 + j · X3 = Z3 · 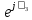 = 161,29 + j · 0 = 161,29· = 161,29 + j · 0 = 161,29·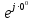 Ом. Ом.Схема включения приемников в трехфазную сеть Т 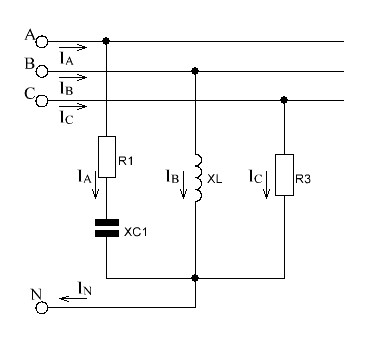 ак как по условию задачи Uлин = 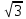 · Uф, 220 В = · Uф, 220 В = 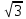 ·127 В, то для включения приемников используется соединение звездой, а поскольку приемники не симметричны, то необходим нейтральный провод, который обеспечивает равенство по величине фазных напряжений приемников (рисунок 4.1). ·127 В, то для включения приемников используется соединение звездой, а поскольку приемники не симметричны, то необходим нейтральный провод, который обеспечивает равенство по величине фазных напряжений приемников (рисунок 4.1).Рисунок 4.1  Схема включения приемников треугольником Схема включения приемников треугольникомРасчет фазных токов каждого приемника, тока в нулевом проводе Запишем комплексные значения фазных напряжений сети: 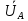 = 127 · = 127 · 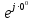 В; В; 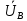 = 127 · = 127 · 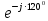 В; В; 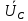 = 127 · = 127 · 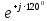 В. В.Тогда линейные напряжения сети запишем в следующем виде: 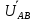 = 220 · = 220 · 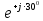 В; В; 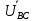 = 220 · = 220 · 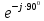 В; В; 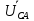 = 220 · = 220 · 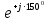 В. В.Фазные токи однофазных приемников: 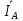 = = 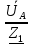 = = 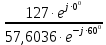 = 2,20472 · = 2,20472 ·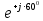 = == 2,20472 · cos(+600) + j · 2,20472 · sin(+600) = = 2,20472 · 0,5 + j · 2,20472 · 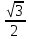 = 1,10236 + j · 1,90934 A; = 1,10236 + j · 1,90934 A;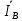 = = 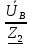 = = 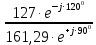 = 0,787402 · = 0,787402 ·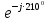 = =  0,681910 + j · 0,393701 A; 0,681910 + j · 0,393701 A;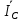 = = 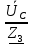 = = 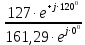 = 0,787402 · = 0,787402 ·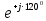 = =  0,393701 + j · 0,681910 A. 0,393701 + j · 0,681910 A.Ток нейтрального провода: 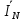 = = 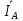 + +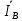 + +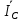 = 1,10236 + j · 1,90934 = 1,10236 + j · 1,90934 0,681910 + j · 0,393701 0,681910 + j · 0,393701   0,393701 + j · 0,681910 =0,023149 + j · 2,97954 =2,97963· 0,393701 + j · 0,681910 =0,023149 + j · 2,97954 =2,97963·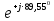 A. A.Расчет мощностей Определяем активную, реактивную и полную мощности. Активная мощность: P = P1 +P2+P3. P2 = 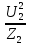 · cos2 = · cos2 = 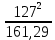 · 0 = 0 Вт; · 0 = 0 Вт;P = 140 + 0 + 100 = 240 Вт. Реактивная мощность: Q = Q1 +Q2+Q3. Q1 = 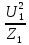 · sin1= · sin1= 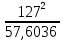 · ( · ( 0,866025)= 0,866025)=  242,487 вар; 242,487 вар;Q3 = 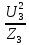 · sin3= · sin3= 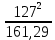 · 0 = 0 вар; · 0 = 0 вар;Q =  242,487 + 100 + 0 = 242,487 + 100 + 0 =  142,487 вар. 142,487 вар.Полная мощность: S = 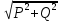 = = 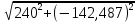 = 279,11 BA. = 279,11 BA.Построение векторной диаграммы Для построения векторной диаграммы выбираем масштаб токов и напряжений: М(I) = 0,5 А/см, М(U) = 36 В/см. Построение на комплексной плоскости начинаем с векторов фазных напряжений 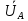 , , 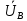 , , 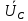 Рассчитаем длину векторов напряжений: Рассчитаем длину векторов напряжений:l(UA) = 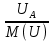 = = 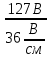 = 3,5 см, = 00; = 3,5 см, = 00;l(UB) = 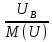 = = 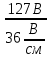 = 3,5 см, = -1200; = 3,5 см, = -1200;l(UС) = 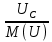 = = 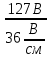 = 3,5 см, = +1200. = 3,5 см, = +1200.Линейные напряжения строим, учитывая, что 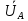 = = 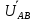 - - 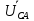 , ,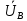 = = 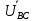 - - 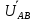 , ,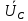 = = 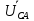 - - 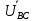 . .Найдем длину линейных напряжений: l(UAB) = 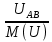 = = 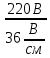 = 6,1 см, = +300; = 6,1 см, = +300;l(UBC) = 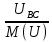 = = 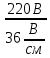 = 6,1 см, = -900; = 6,1 см, = -900;l(UCA) = 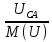 = = 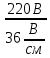 = 6,1 см, = +1500. = 6,1 см, = +1500.Далее откладываем фазные токи 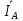 , , 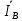 , , 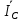 и ток в нейтральном проводе и ток в нейтральном проводе 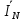 . Рассчитаем их длину: . Рассчитаем их длину:l(IA) = 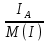 = = 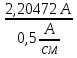 = 4,4 см, = +600; = 4,4 см, = +600;l(IB) = 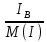 = = 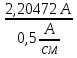 = 1,6 см, = -2100; = 1,6 см, = -2100;l(IC) = 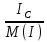 = = 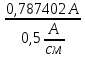 = 1,6 см, = +1200; = 1,6 см, = +1200;l(IN) = 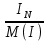 = = 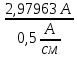 = 6 см, = +900. = 6 см, = +900. |
