Шпоры по Схемоте. 1. счетчики основные параметры и классификация

• Название: 1. счетчики основные параметры и классификация
• Анкор: Шпоры по Схемоте.doc
• Дата: 19.09.2017
• Размер: 8.5 Mb.
• Имя файла: Шпоры по Схемоте.doc
• Тип: Документы; #8683
• Категория: Электротехника. Связь. Автоматика
• страница: 1 из 4

1. СЧЕТЧИКИ Основные параметры и классификация

Счетчиком называется функциональный узел ЭВМ, предназначенный для подсчета числа входных сигналов и хранения результата счета в двоичном коде. Счетчики выполняются на элементах памяти (триггерах), образующих двоичные разряды, и элементах комбинационной логики.

Счетчики могут быть с естественным и произвольным порядком счета. При естественном порядке счета результат счета изменяется на единицу при поступлении на вход счетчика каждого сигнала (импульса). В счетчиках с произвольным порядком счета, называемых также пересчетными устройствами, при поступлении входных сигналов результат счета может изменяться произвольно в соответствии с заданным законом.

Основными параметрами счетчиков являются модуль счета (коэффициент пересчета, емкость счетчика) Ксч и быстродействие. Модулем счета называют число состояний, которые он приобретает под действием входных сигналов. Если счетчик начал считать с начального состояния, то через каждые Кcч входных сигналов он снова возвращается в начальное состояние, а на его выходе появляется сигнал Ксч-ичного переноса. Быстродействие счетчика определяется разрешающей способностью и временем установки. Разрешающая способность t _Р характеризуется периодом входных импульсов Т_СЧ, при котором счетчик еще работает без сбоев, а время установки t_УСТ — интервалом времени от момента поступления сигнала на вход счетчика до завершения перехода счетчика в новое состояние.

По значению модуля счета счетчики делятся на двоичные (Ксч =2ⁿ, где n число разрядов), двоично-кодированные (имеют произвольный модуль счета, но все состояния кодируются двоичными кодами), счетчики с одинарным кодированием (состояние счетчика определяется местом расположения единственной единицы), счетчики с унитарным кодированием (состояние счетчика представлено числом единиц) и др.

По направлению счета счетчики могут быть суммирующими (прямого счета), вычитающими (обратного счета) и реверсивными, т.е. способными работать как в режиме суммирования, так и в режиме вычитания.

По структурной организации счетчики делятся на последовательные (асинхронные), параллельные (синхронные) и параллельно-последовательные.

Помимо входа для приема подсчитываемых сигналов счетчик может иметь вход общего сброса R и входы данных D_i для параллельной загрузки произвольного кода. В последнем случае для осуществления загрузки предусматривается еще один вход — вход разрешения параллельной загрузки PL (parallel 1оаd).

Счетчики используются в ЭВМ для осуществления последовательного выполнения команд программы, подсчета числа циклов выполненных операций, образования адресов при обращении к запоминающим устройствам, в качестве делителей частоты в цифровых электронных часах и частотомерах и др.

2-3 Последовательные счетчики

В счетчиках, показанных на рис.12.1, используется непосредственная связь между выходами и входами триггеров. Поскольку каждый триггер (кроме первого) переключается выходным сигналом предыдущего, в таких счетчиках нет специальных схем формирования сигналов переноса или заема: их роль выполняют сигналы с выходов старшего разряда. Наращивание разрядности достигается путем последовательного подключения нужного количества триггеров. Однако несмотря на эти достоинства, а также простоту схемной реализации, область применения последовательных счетчиков с непосредственными связями ограничивается пределом их быстродействия.

На рис. 12.2 приведены временные диаграммы трехразрядного суммирующего счетчика, выполненного по схеме рис. 12.1, а.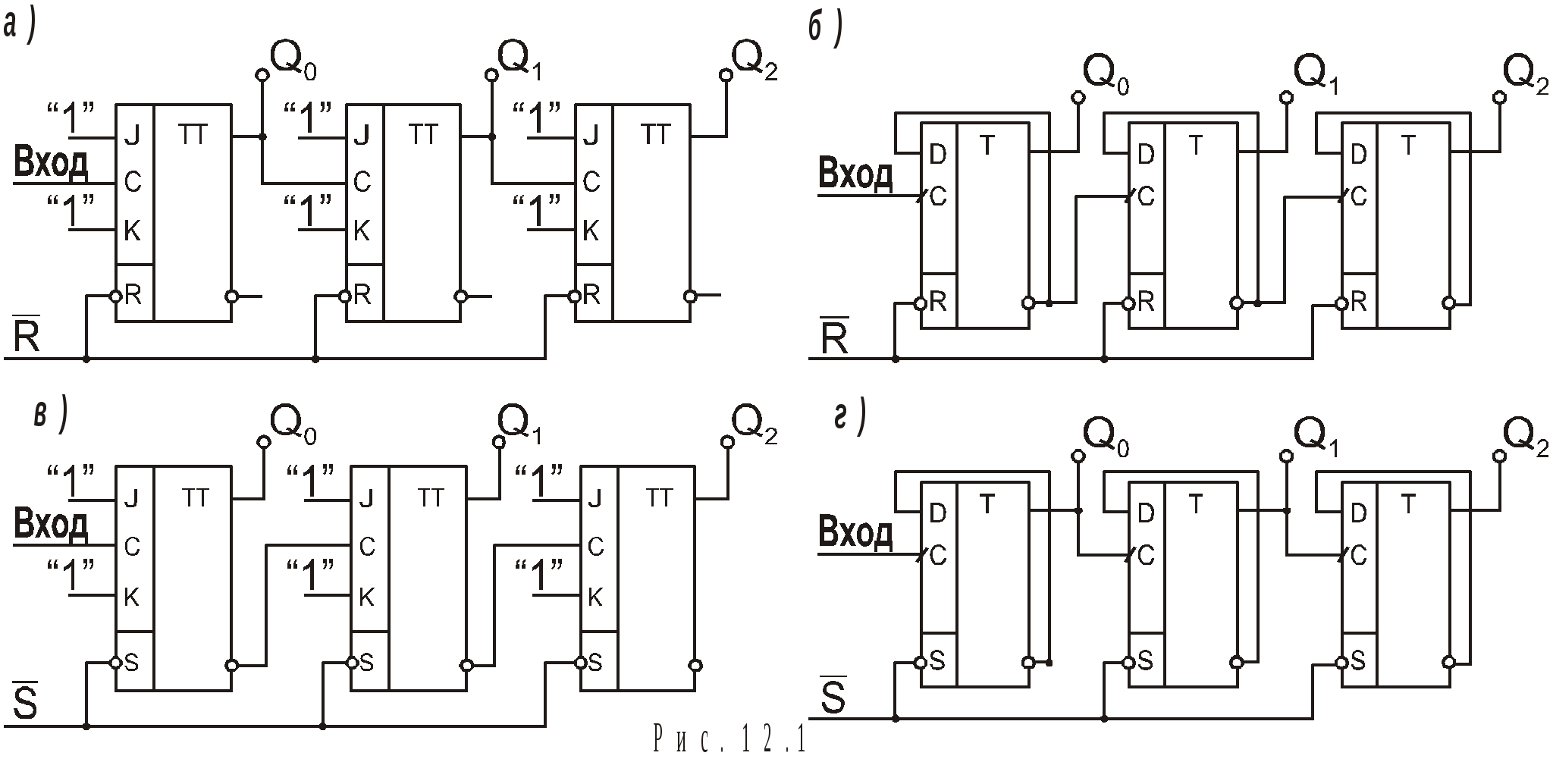



Параметр t_ТГ характеризует задержку переключения триггера при поступлении на его вход отрицательного перепада напряжения. Наличие этой задержки вызывает появление "ошибочных" результатов, не предусмотренных таблицей его функционирования (см. табл. 12.1). Так, например, после окончания действия второго входного импульса перед правильным состоянием Q₂Q₁Q₀=010 на некоторое время возникает неправильное состояние Q₂Q₁Q₀=000, соответствующее переходным процессам в триггерах нулевого и первого разрядов. Из-за переходных процессов при переключениях триггеров всех трех разрядов после окончания четвертого (а также восьмого) входного импульса установлению правильного состояния Q₂Q₁Q₀=100 предшествуют два неправильных: 010 и 000. Следовательно индикацию результата счета в таком счетчике (а значит, и интервал между входными импульсами) следует осуществлять не ранее, чем через время t=3t_ТГ. При этом максимальная частота следования входных импульсов определяется формулой:

,

где t_И - длительность импульса.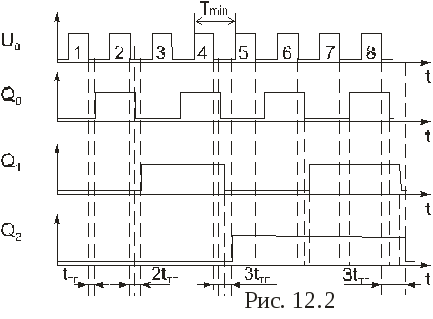



С увеличением разрядности счетчика увеличивается время задержки переключения триггера n-го разряда относительно среза входных импульсов, поэтому для n-разрядного счетчика с последовательным переносом максимальная частота входных импульсов будет равна:

.

На диаграммах виден и режим деления частоты: каждый последующий триггер переключается вдвое реже, чем предыдущий. Поскольку предыдущий триггер выполняет роль генератора импульсов для последующего, то максимальная частота входных импульсов в режиме деления частоты ограничивается возможностями триггера младшего разряда и равна 1/t_ТГ. Задержки переключения триггеров последующих разрядов вызовут лишь появление фазовых сдвигов между входной и выходной последовательностями импульсов.

Примером интегрального двоичного счетчика с непосредственными связями может служить микросхема К155ИЕ5 (рис.  12.3,  а). Она представляет собой 4-разрядный двоичный счетчик, выполненный на двухступенчатых JK-триггерах с двумя счетными входами С₁ и С₂ и двумя входами сброса в нуль R₁ и R₂. Выход Q₀ внутренне не соединен с последующими триггерами, что дает возможность использовать схему в качестве 3-разрядного или 4-разрядного двоичного счетчика. В первом случае счетные импульсы подают на вход С₂, а во втором – на вход С₁, предварительно объединив выход Q₀ со входом C₂. Входы сброса R₁ и R₂ обеспечивают сброс счетчика в нулевое состояние при R₁=R₂=1. При выполнении операции счета на одном из входов R₁ или R₂ ( или на обоих ) должен присутствовать потенциал низкого уровня.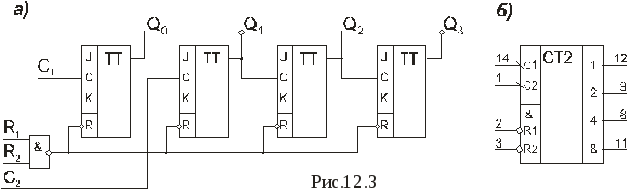



Условное обозначение счетчика дано на рис. 12.3, б.

4. Счётчики с параллельным переносом

Из табл. 12.1 видно, что в суммирующем счетчике при поступлении на вход очередного счетного импульса переключаются все те триггеры, перед которыми все более младшие триггеры находились в состоянии 1, а также первый, следующий за ними (старший) погашенный триггер. Это свойство лежит в основе построения многоразрядных счетчиков с параллельным переносом между разрядами. На входе каждого триггера, кроме первого, включается конъюнктор. На входы каждого конъюнктора подаются сигналы с прямых выходов всех предыдущих триггеров и счетные импульсы (рис. 12.4, а). Такой счетчик имеет один вход и является асинхронным. Его недостатком является задержка переключения триггеров относительно среза входного импульса, обусловленная задержкой, вносимой конъюнкторами. При совместной работе такого счетчика с другими синхронными устройствами эту задержку необходимо учитывать. От указанного недостатка свободен синхронный счетчик с параллельным переносом (рис. 12.4, б). Его можно выполнить на синхронных двухступенчатых JK-триггерах. Подготовка триггеров счетчика к переключению осуществляется потенциальным сигналом СЕ (count enable - разрешение счета), который может быть сформирован с любой задержкой в пределах такта синхронизации. Переключение триггеров будет проходить строго по отрицательному фронту синхроимпульса, поступающего на вход С. Выход переноса CR используется при наращивании разрядности счетчика. Если счетчик составляется из групп, показанных на рис. 12.4, б, то выход CR (выход схемы формирования сигнала переноса) одной группы объединяется со входом СЕ следующей, более старшей группой.

Некоторые счетчики (например, К155ИЕ9) имеют по два входа разрешения (рис. 12.4, в): СЕТ (count enable trickte - разрешение переноса) и СЕР ( count enable parallel - параллельное разрешение счета). Такой счетчик получается, если фрагмент схемы рис. 12.4, б, обведенный штриховой линией, заменить фрагментом, показанным на рис. 12.4, в. Вход СЕТ разрешает формирование переноса CR. При наращивании разрядности выход CR соединяется со входом СЕТ следующей более старшей группы. Вход СЕР при наличии сигнала СЕТ разрешает переключение триггеров при поступлении синхросигнала на их входы С, которые выполнены также, как и в схеме на рис. 12.4, б. Входы СЕР всех групп можно объединить и подключить к источнику внешнего разрешающего сигнала. Если этого не требуется, то входы СЕР второй и всех следующих групп подключаются к выходу CR первой (самой младшей) группы.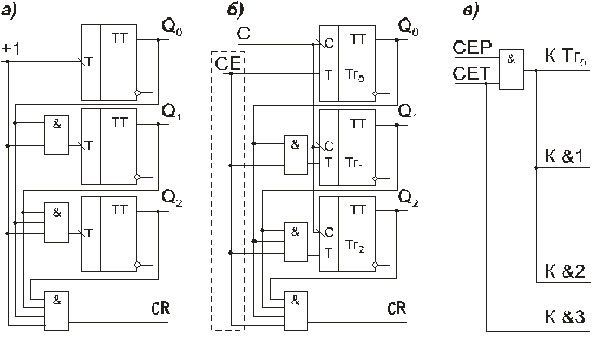



Для получения вычитающих счетчиков необходимо использовать не прямые, а инверсные выходы триггеров.

5. Счетчики с параллельным занесением информации

В таких счетчиках имеются дополнительные входы параллельного занесения (параллельной загрузки) D_i, сигналы с которых заносятся в триггеры при разрешающем сигнале на входе разрешения параллельной загрузки 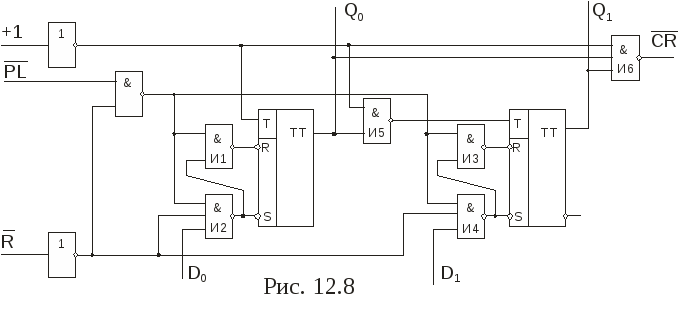. На рис. 12.8 приведена схема двухразрядного суммирующего счетчика с входами параллельной загрузки D₀ и D₁. При элементы И1...И4 закрыты, на установочных входах и триггеров действуют нейтральные комбинации сигналов и счетчик работает в режиме суммирования по сигналам, поступающим на вход "+1". Если на вход разрешения параллельной загрузки подать сигнал , то элементы И1...И4 откроются, на установочные входы первого триггера поступят сигналы =, =, а на входы второго- сигналы , , под действием которых счетчик примет состояние Q₁Q₀=D₁D₀.



Инверсный вход сброса R служит для перевода счетчика в нулевое состояние. При R=1 на выходах элемента И2 и И4 устанавливается уровень логической 1, а на выходах элементов И1 и И3 – уровень логического 0, вследствие чего на установочных входах обоих триггеров устанавливаются комбинации сигналов , переводящие триггеры в нулевое состояние.

По подобной схеме выполнен интегральный 4-разрядный счетчик ИЕ15, имеющийся в сериях 530, К555, КР531.

Наличие входов параллельной загрузки существенно расширяет функциональные возможности счетчика, поэтому такие входы имеются у большинства интегральных счетчиков.

7. Счетчики с произвольным модулем счета и управляемым сбросом

Все рассмотренные ранее счетчики имеют "жесткую" структуру, при которой изменение модуля счета Кcч связано с коммутационными изменениями всей схемы. Однако можно построить счетчики, в которых изменение модуля счета осуществляется более простым способом, практически не вносящим изменений в основную схему счетчика. Этого можно достигнуть, если осуществить управляемый сброс счетчика в нулевое состояние. Например, если имеется четырехразрядный двоичный счетчик с Ксч=16, то для его преобразования в счетчик с модулем счета Ксч=13 необходимо, чтобы после состояния 12 следующий входной импульс сбрасывал его в 0, возвращая к началу цикла счета. Если счетчик выполнен на JK-триггерах, то для сброса в 0 должен вырабатываться сигнал R, под действием которого на входах всех триггеров устанавливалась бы комбинация сигналов J=0, К=1. Следовательно, схемы управления на входах триггеров двоичного счетчика с параллельным переносом, формирующие сигналы



где: i = 1,2,... ,n-1; n — число разрядов счетчика, должны быть преобразованы в схемы управления, формирующие сигналы

.

Согласно этим выражениям схема i-го разряда счетчика будет иметь вид, показанный на рис. 12.11. Сигнал R сброса счетчика в 0 вырабатывается дополнительным конъюнктором при установке на его входах двоичного кода, равного значению Ксч -1. Это достигается подключением входов дополнительного конъюнктора к прямым выходам триггеров соответствующих разрядов.

В 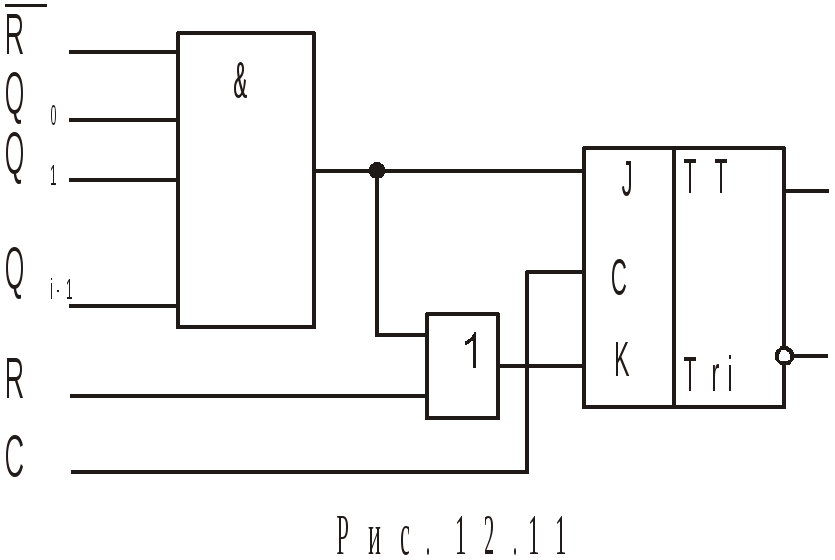качестве примера, иллюстрирующего рассмотренный способ, на рис. 12.12 показана схема параллельного суммирующего счетчика с модулем счета Ксч=6.

При достижении счетчиком состояния 5 (Q₂=1, Q₁=0, Q₀=1) на выходе конъюнктора ИЗ образуется сигнал R=1, который устанавливает на входах каждого триггера комбинацию сигналов J=0, К=1. Под действием этих комбинаций очередной импульс, поступивший на вход С, осуществляет установку всех триггеров счетчика в нулевое состояние.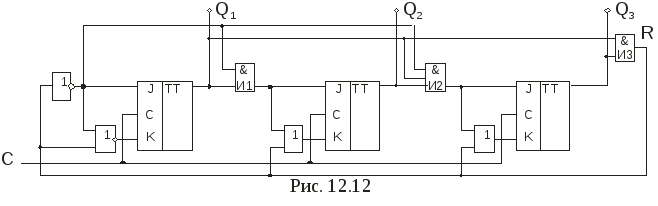



Схема счетчика с произвольным модулем счета может быть значительно упрощена, если в нем использовать триггеры с установочными входами. Примером может служить схема счетчика с модулем счета Кcч=11, выполненного на основе суммирующего 4-разрядного счетчика с параллельным переносом на двухступенчатых JK-триггерах с установочными входами (Рис. 12.13). На входы постоянно заведены уровни логической 1, а на входы R поступает сигнал с выхода дополнительного конъюнктора. При счете от 0 до 10 конъюнктор закрыт и сигнал с его выхода R=1 не оказывает влияния на работу счетчика. При поступлении очередного импульса на входы С триггеров счетчик устанавливается в состояние 11 (Q₃Q₂Q₁Q₀=1011). При этом на выходе конъюнктора образуется сигнал , который сбрасывает триггеры всех разрядов в нулевое состояние и одновременно служит сигналом переноса.



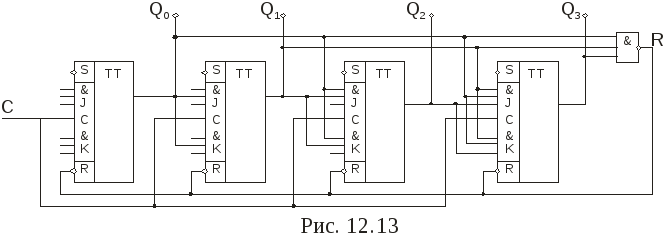Достоинством счетчиков с управляемым сбросом является естественная двоичная последовательность кодов.

8. Генераторы чисел на основе счетчиков

Такие последовательностные устройства называют также кольцевыми распределителями сигналов. Последовательность двоичных чисел, образуемая на их выходах, часто используется в цифровых системах как последовательность сигналов. управляющих работой других узлов. Число состояний, которое может принимать генератор, называется длиной последовательности чисел L. С этой точки зрения любой счетчик можно рассматривать как генератор определенной последовательности чисел, у которого L = Ксч. Например, счетчик с модулем счета Ксч=8 (рис. 12.12) является генератором последовательности чисел 0-1 -2-3-4-5-6-7.

Число разрядов счетчика, используемого в качестве генератора некоторой последовательности чисел, определяется либо числом разрядов двоичного кода генерируемых чисел, либо длиной последовательности этих чисел. В первом случае синтез счетчика осуществляется по методике, используемой при синтезе счетчика с произвольным модулем счета. При этом последовательно записываются состояния, принимаемые счетчиком, и для каждого перехода определеяются функции входов всех триггеров. Во втором случае счетчик рассматривается как двоичный (суммирующий или вычитающий), но к его выходам подключается комбинационная схема, пересчитывающая его состояния в состояния заданной последовательности.

В качестве примера рассмотрим генератор чисел 5-3-11-7. Так как L=4, то в качестве основы генератора используется 2-разрядный суммирующий счетчик с модулем счета Ксч=4. К выходам Q₁ и Q₀ подключим комбинационную схему, преобразующую состояния счетчика 0-1-2-3 в последовательность чисел 5-3-11-7. Поскольку наибольшее число последовательности 11 представляется четырехразрядным двоичным кодом, то комбинационная схема должна содержать четыре выхода А,В,С,D. Считая выход А младшим разрядом, а выход D- старшим, составим таблицу истинности комбинационной схемы (табл. 12.4), на основании которой, используя известные методы минимизации булевых функций, получим уравнения выходов:

.

Q1	Q0	D	C	B	A
0 0 1 1	0 1 0 1	0 0 1 0	1 0 0 1	0 1 1 1	1 1 1 1

Структура генератора последовательности чисел 5-3-11-7 с комбинационной схемой в базисе И-НЕ, синтезированного с использованием уравнений (12.2), показана на рис. 12.15.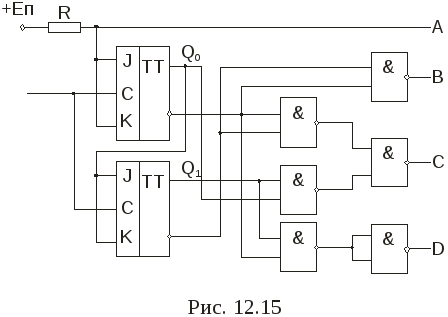