Шпоры по Схемоте. 1. счетчики основные параметры и классификация
 Скачать 8.5 Mb.
|
|
Линейные дешифраторы В линейных дешифраторах каждое уравнение системы (14.1) реализуется отдельным ЛЭ. В качестве примера рассмотрим линейный дешифратор 3-8, у которого функции выходов имеют вид: 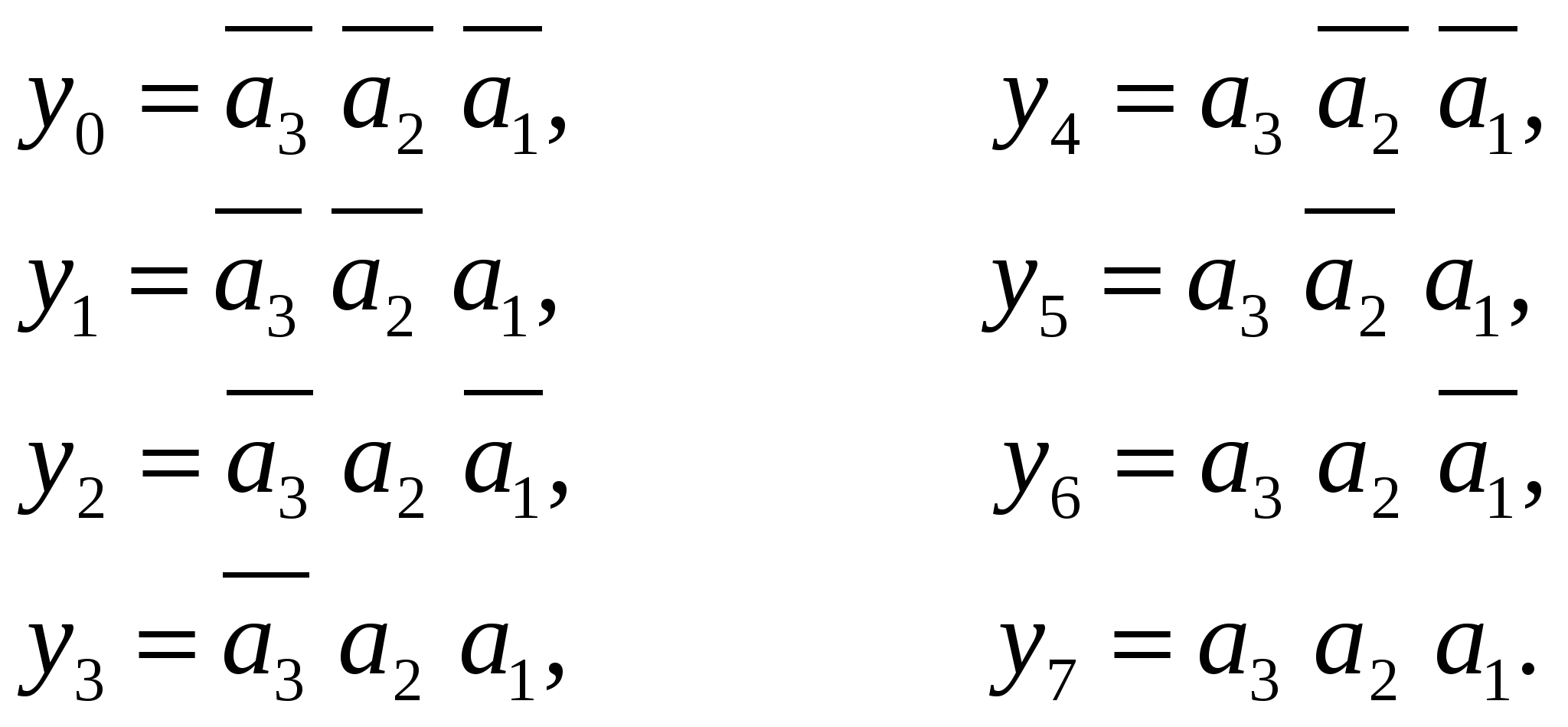 Эти уравнения могут быть реализованы с помощью восьми трехвходовых элементов И, как показано на рис.14.2. У такого дешифратора активным уровнем является высокий уровень. Именно такой уровень будет на одном из выходов, определяемом значением числа 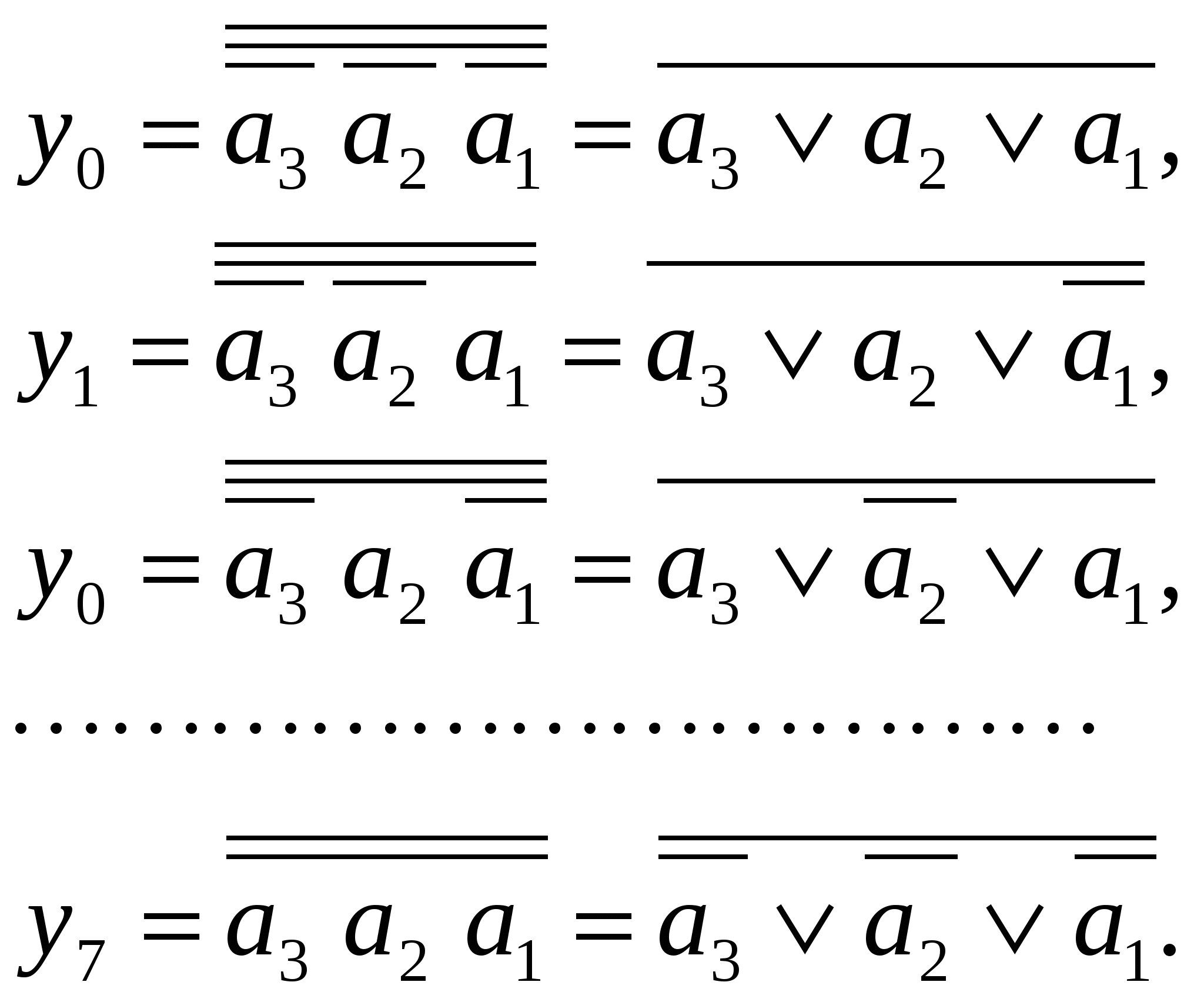 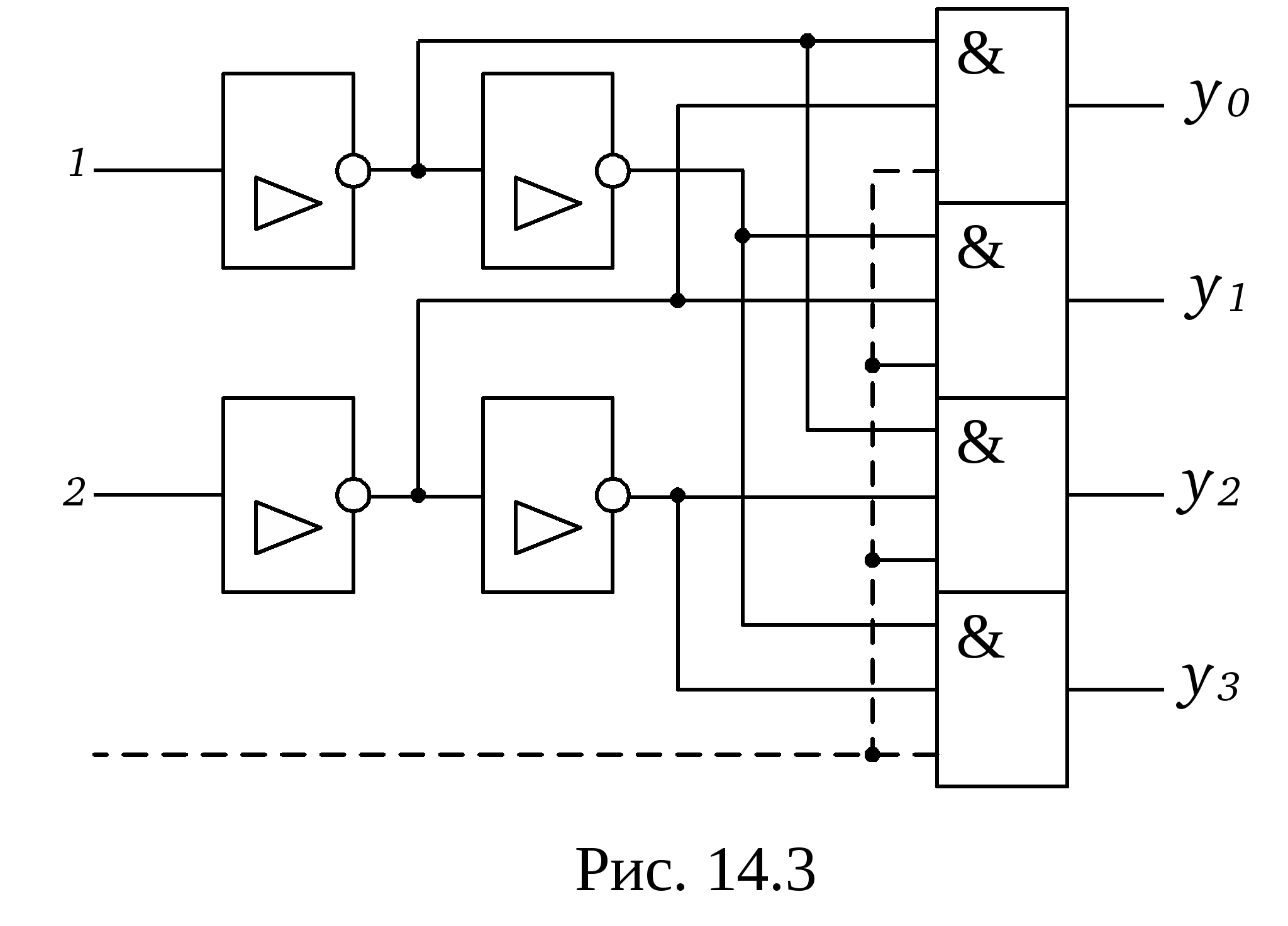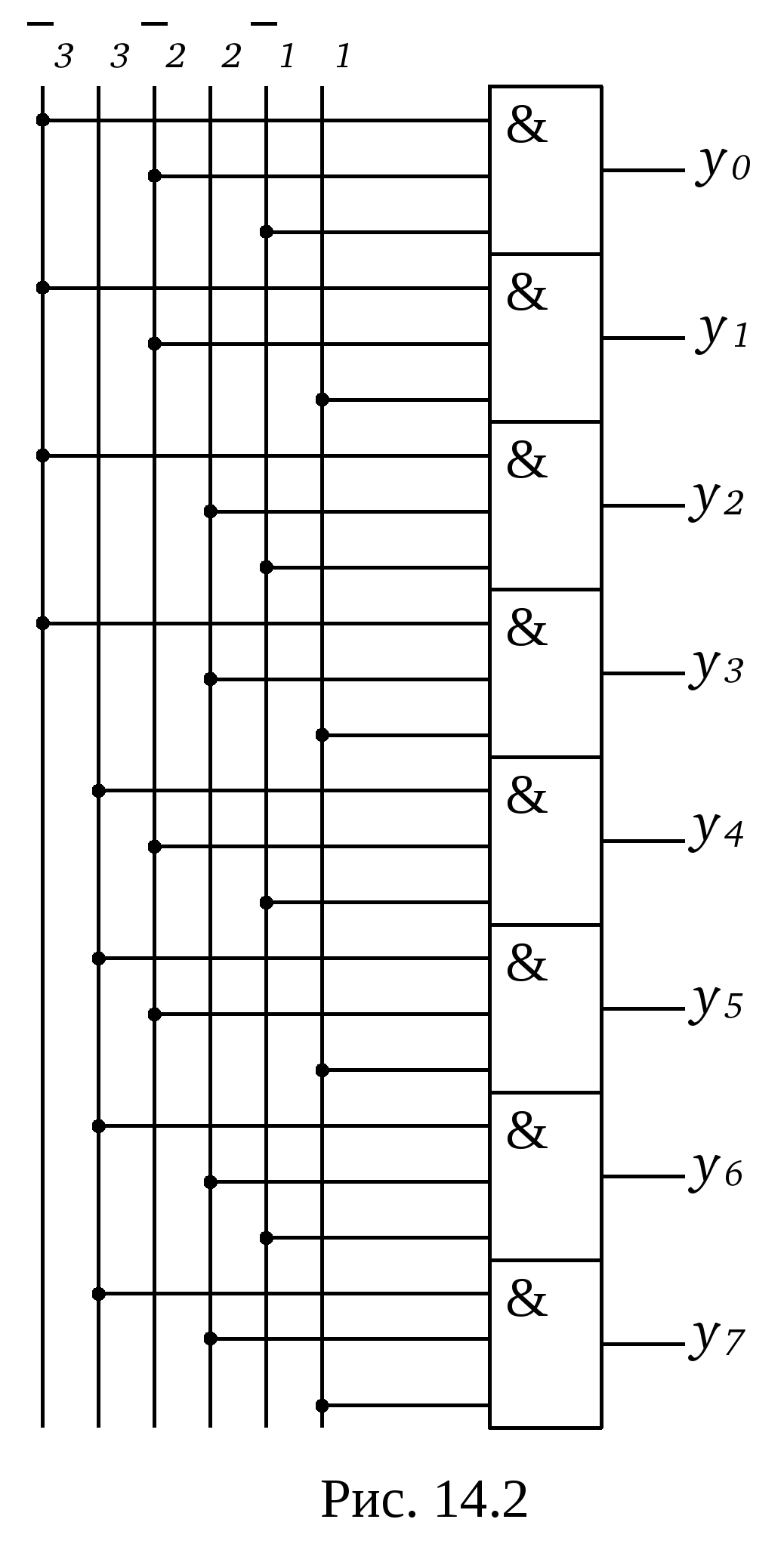, в то время как на всех остальных выходах будут напряжения низкого уровня. Линейный дешифратор может быть реализован на ЛЭ ИЛИ-НЕ. Для этого следует преобразовать уравнения (14.1), воспользовавшись, например, правилами де Моргана. Для дешифратора 3-8 эти преобразования дадут:   Достоинством линейного дешифратора является его высокое быстродействие, определяемое временем задержки tздр.р.ср. одного ЛЭ. Недостаток - увеличение числа входов каждого ЛЭ с ростом разрядности. Д 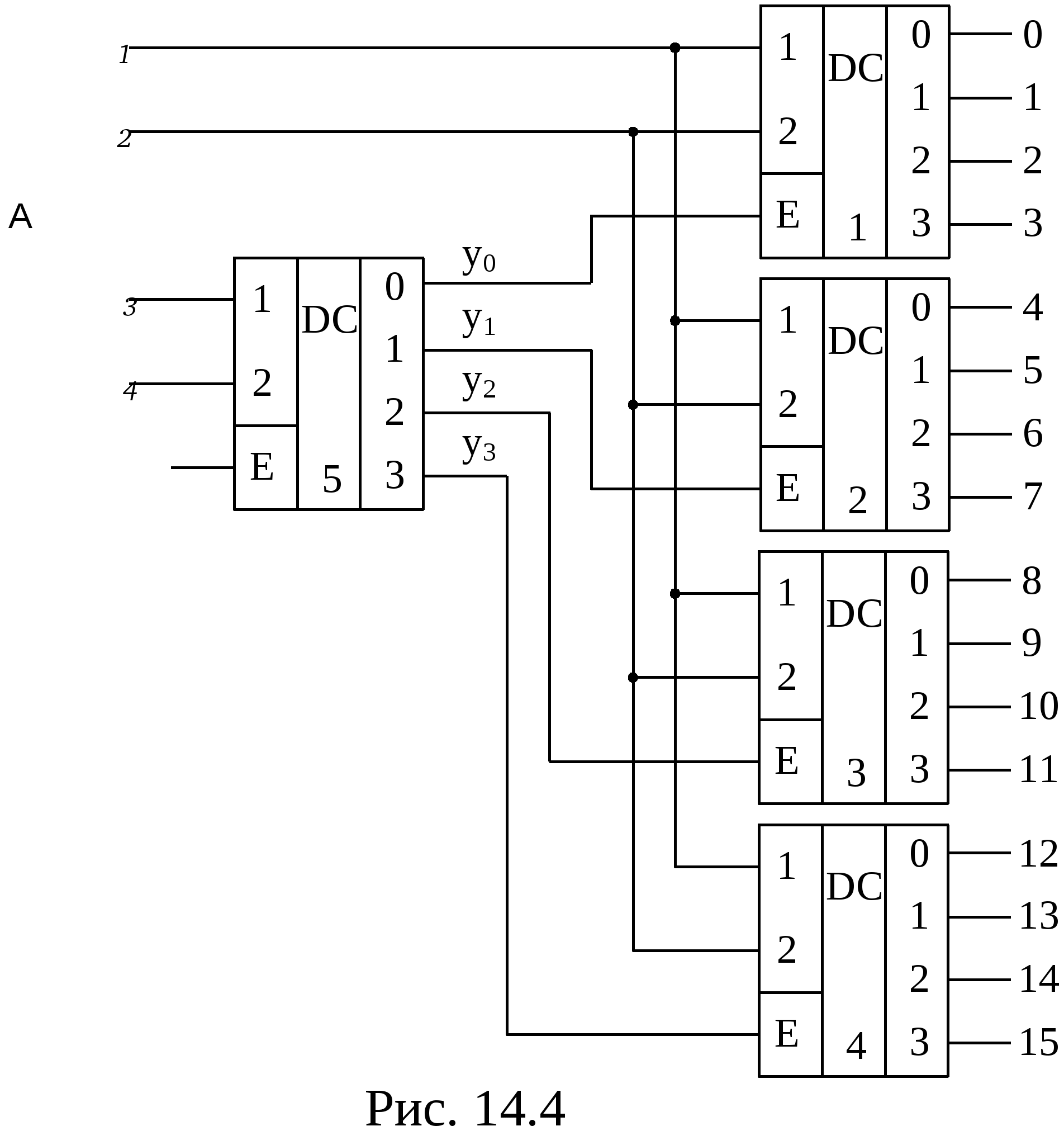 ешифратор чаще всего подключается к выходным разрядам счетчика или регистра. При этом, как это видно из рис. 14.2, каждый разряд источника сигнала нагружается на n2=2m/2 входов ЛЭ дешифратора, что может существенно повлиять на помехоустойчивость. Поэтому входы дешифратора обычно делаются единичными с последующим размножением внутри микросхемы, как показано на рис. 14.3 для дешифратора 2-4. Значок ▷ внутри УГО означает, что используются инверторы с умощенным выходом. Если использовать не двухвходовые, а трехвходовые ЛЭ И, то третьи входы можно объединить и использовать в качестве входа разрешения. Такие дешифраторы называются стробируемыми. Выполненный таким образом стробирующий вход обладает тем достоинством, что не вносит дополнительной задержки в дешифратор, т.е. не влияет на его быстродействие. Недостаток - требуется увеличение числа входов ЛЭ на 1. Работа стробируемых дешифраторов описывается логическими уравнениями, подобными уравнениям (14.1), но содержащими дополнительно сигнал разрешения Е: Для увеличения разрядности дешифраторов можно использовать их каскадное соединение. На рис. 14.4 показан дешифратор на 4 входа и 16 выходов, полученный каскадным соединением четырех стробируемых дешифраторов «2-4». Дешифрируемый двоичный код 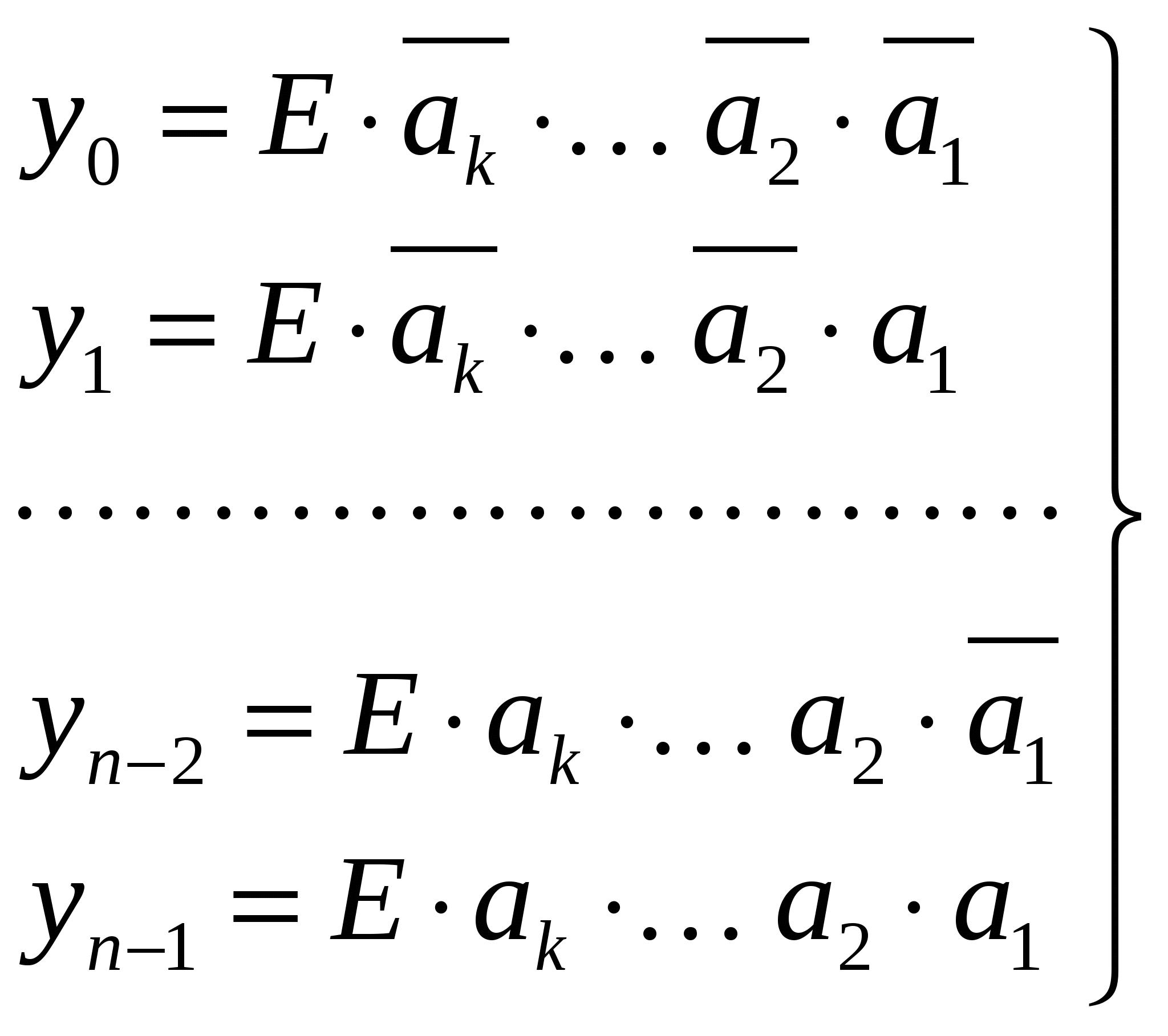 возбуждает один из выходов дешифратора. Если А ≤ 3, то работает DC1 (у0 = 1, y1 = у2 = у3 = 0 ). При 3 ≤ А ≤ 7 работает DC2 (y1 = 1, у0 = у2 = у3 = 0). При 7 ≤ А ≤ 11 работает DC3 (у2 = 1, у0 = у1, = у3 = 0), а при А > 11 - дешифратор DC4 (y3 = 1, y0 = y1 = y2 = 0). (14.2)В сериях ТТЛ и ТТЛШ дешифраторы обычно имеют инверсные выходы, поскольку их реализация осуществляется на элементах И-НЕ, являющихся наиболее технологичными в этих сериях. В КМДП-сериях, выполненных на инверторах, предпочтение имеют устройства, выполненные на элементах ИЛИ-НЕ, и дешифраторы чаще имеют прямые выходы. Многоступенчатые дешифраторы Если каскадное соединение дешифраторов не обеспечивает получение нужной разрядности дешифрируемого адресного кода, то дешифраторы строятся по многоступенчатой схеме. При этом различают прямоугольные и пирамидальные дешифраторы. Рассмотрим пример синтеза прямоугольного дешифратора 4-16, уравнения выходов которого имеют вид: 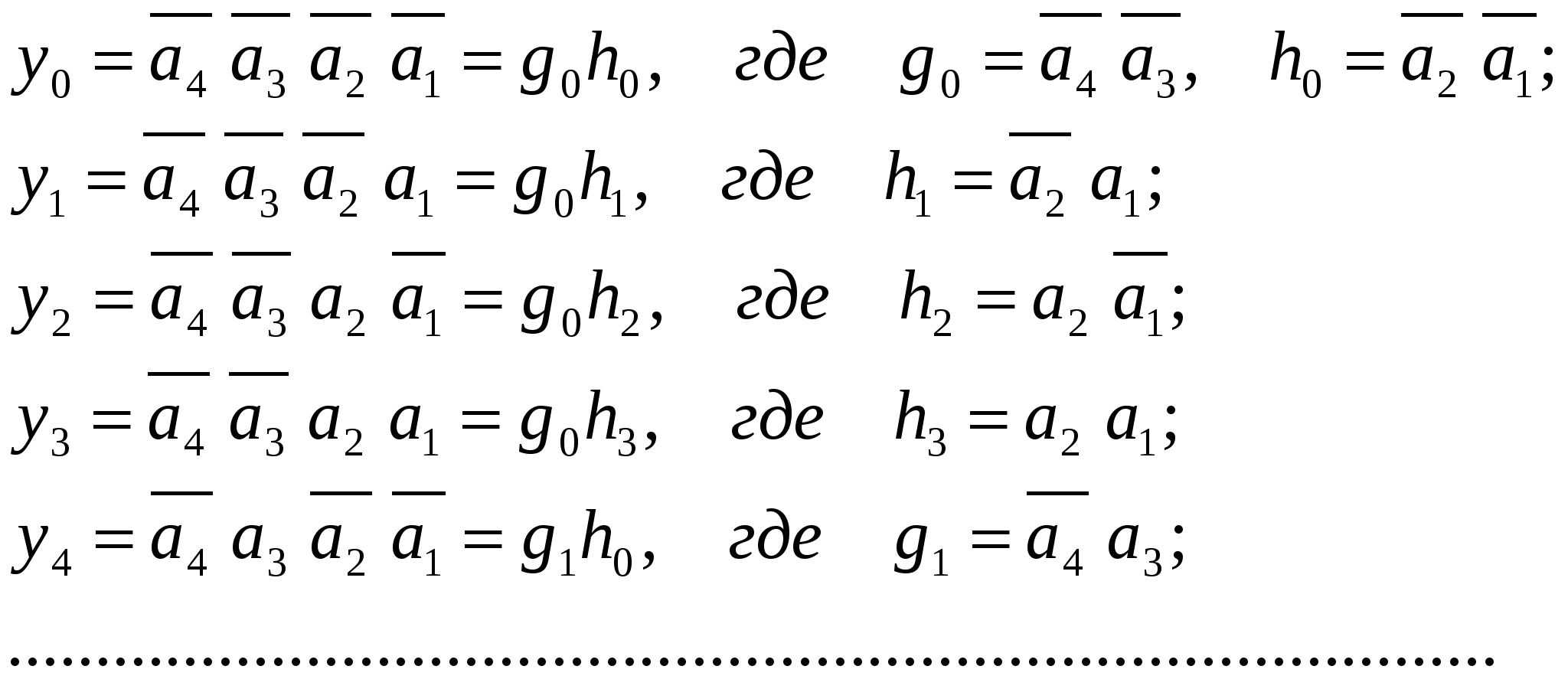 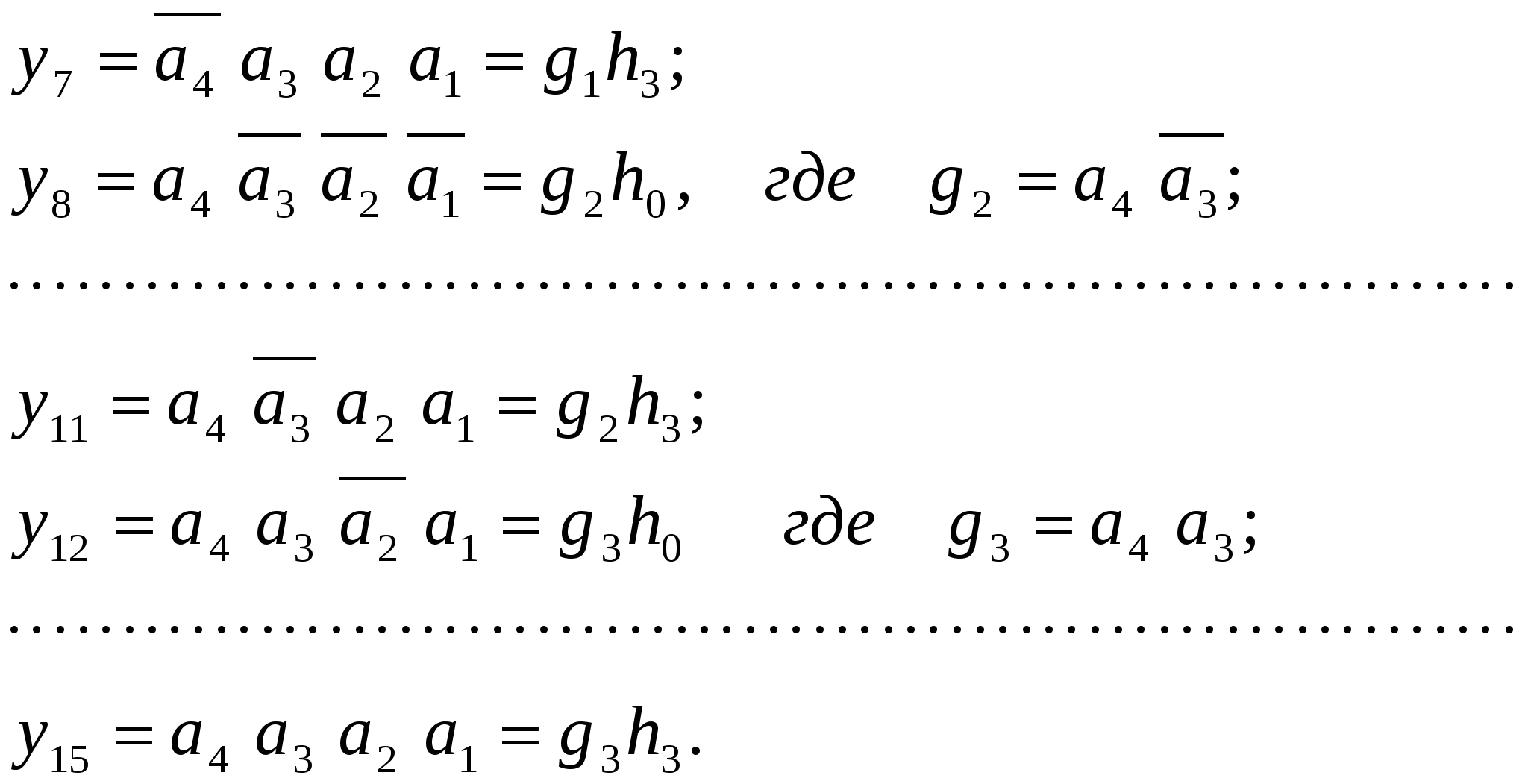 Таким образом, разряды адреса представлены двумя группами (g0…g3 и h0…h3), каждая из которых независимо от другой может расшифровываться своим линейным дешифратором 2-4. Эти дешифраторы образуют первую ступень дешифратора 4- 16. Вторую ступень образует матрица из двухвходовых элементов И , реализующих функции gi hj(рис. 14.5). Делить разряды адреса между дешифраторами первой ступени нужно по возможности поровну: чем ближе прямоугольная матрица к квадратной, тем при том же числе элементов И меньше сумма его строк и столбцов, т.е. меньше число выходов дешифраторов первой ступени. В качестве входа Е всего двухступенчатого дешифратора удобно использовать разрешающий вход одного из дешифраторов первой ступени. При этом запираются все строки или все с  толбцы. Число ступеней может быть больше двух. Но следует иметь в виду, что с ростом числа ступеней увеличивается время задержки дешифратора. Прямоугольные дешифраторы широко применяются в БИС памяти. При проектировании же блоков из готовых микросхем, когда затраты оборудования оцениваются не числом элементов, а числом корпусов, даже большие дешифраторы удобно строить по каскадному принципу. Демультиплексоры Демультиплексором называют комбинационный узел ЭВМ, осуществляющий операцию передачи сигнала с одного информационного входа на один из m=2n выходов, номер которого определяется двоичным кодом на n адресных (управляющих) входах. Работа демультиплексора может быть задана либо таблицей истинности, либо логическими уравнениями: 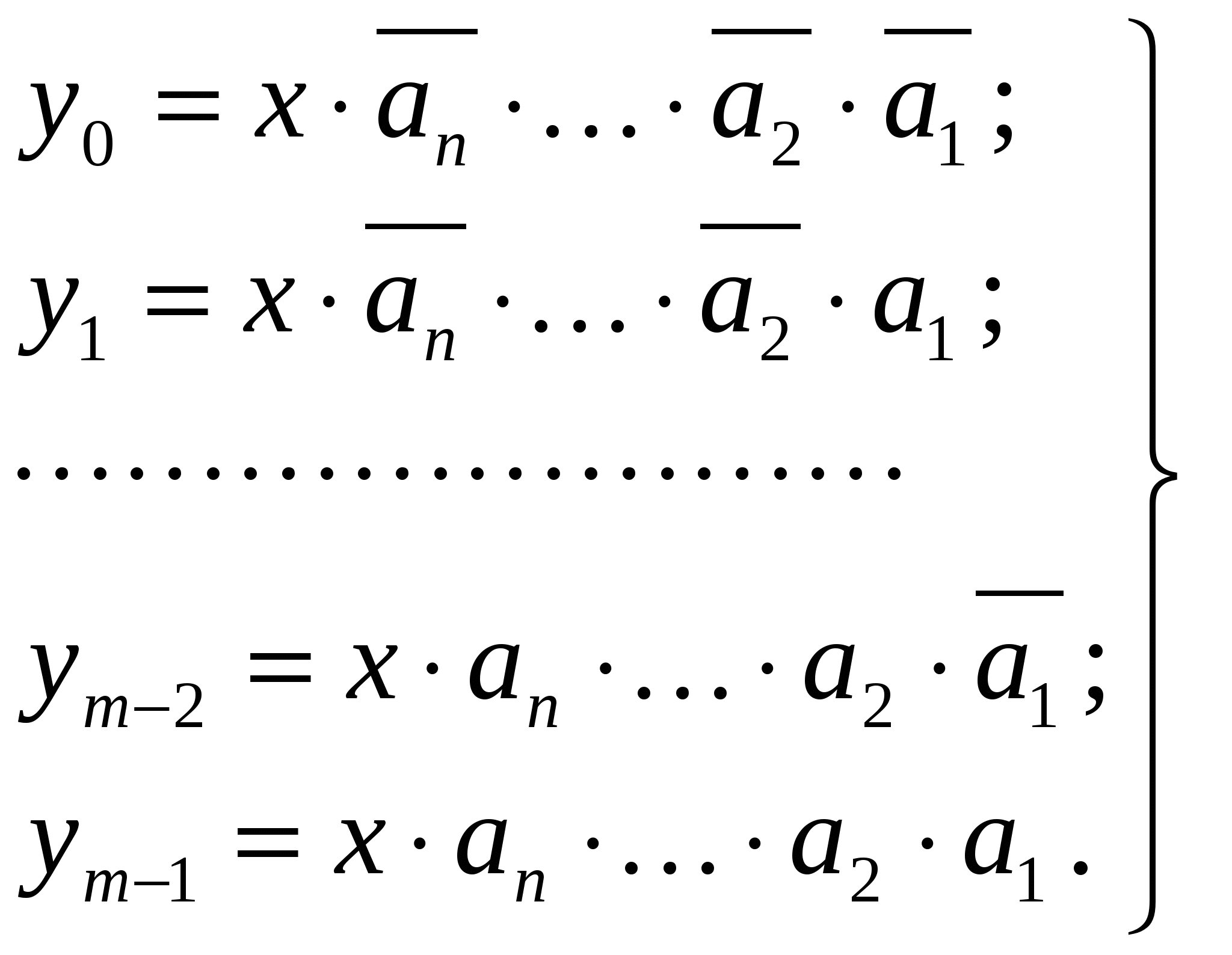 (14.3) в которых a1, a2 ,…, an – сигналы на адресных входах, ах – сигнал на информационном входе. Из сравнения уравнений (14.3) и (14.2) следует, что функцию демультиплексора может выполнять стробируемый дешифратор, если его вход разрешения использовать в качестве информационного. Поэтому как самостоятельные устройства демультиплексоры в интегральном исполнении не выпускаются, а все стробируемые дешифраторы, способные выполнять как функцию дешифрации двоичного кода, так и функцию демультиплексирования сигнала на тот или иной выход, обычно называют дешифраторами-демультиплексорами. На схемах в условном графическом обозначении (УГО) демультиплексор обозначается буквамиDMX в основном поле. В качестве демультиплексора можно использовать и нестробируемый дешифратор, приняв один из адресных входов за информационный (рис 14.6). 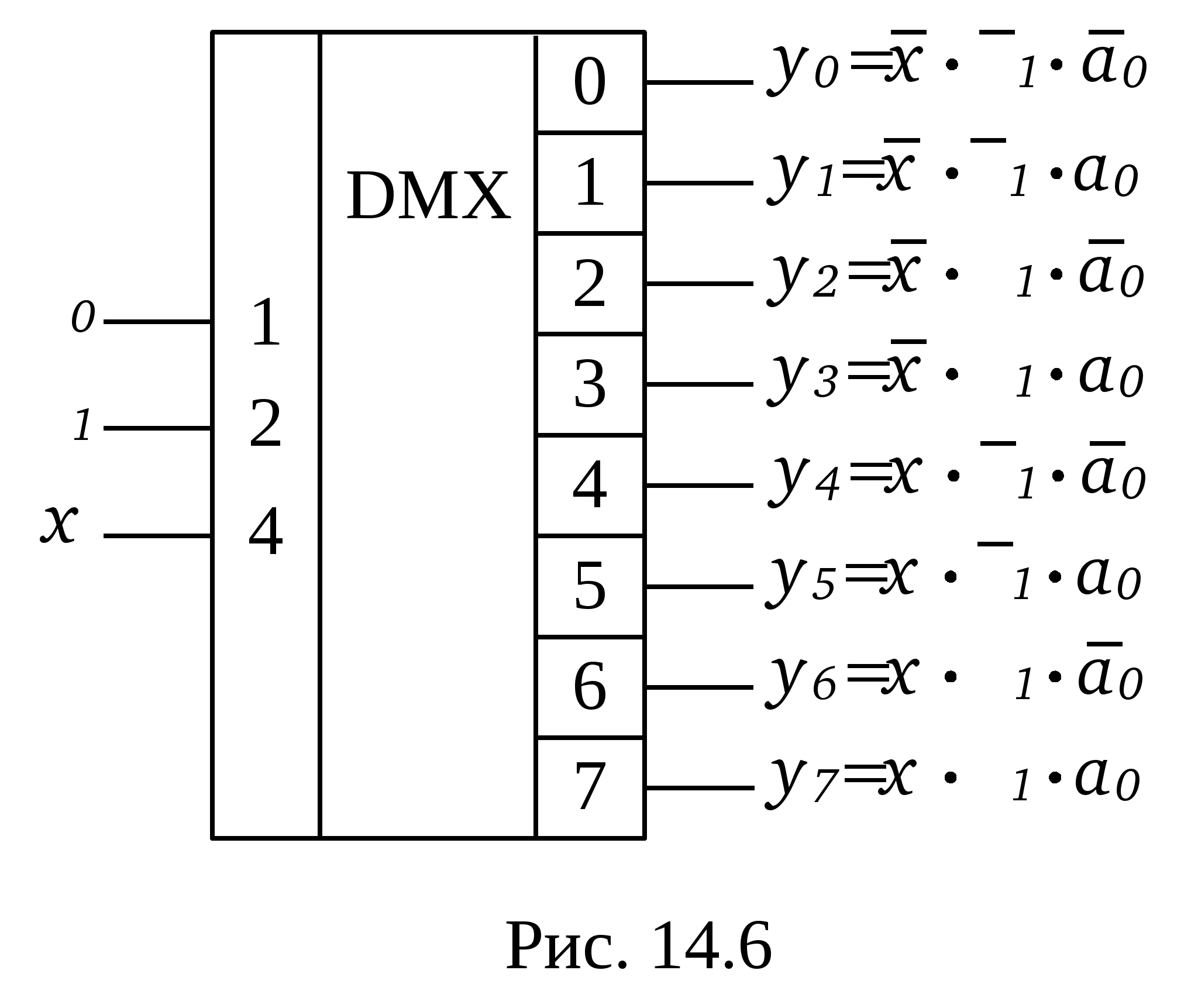 При этом на одной половине его выходов получается прямой входной сигнал x, а на второй - инверсный  .Помимо распределения входного сигнала по нескольким различным адресам демультиплексоры применяются для преобразования последовательного кода в параллельный. 19. Мультиплексоры Мультиплексор - это комбинационный многовходовый функциональный узел с одним выходом. Входы мультиплексора подразделяются на информационные х1, х2, ... хnи адресные, или управляющие а0, а1, а2, ... ak-1. Обычно n=  . Мультиплексор осуществляет функцию, обратную демультиплексору: на выход передается значение переменной того информационного входа, который определяется кодом на адресных входах.Переключательная функция и синтез мультиплексоров Н 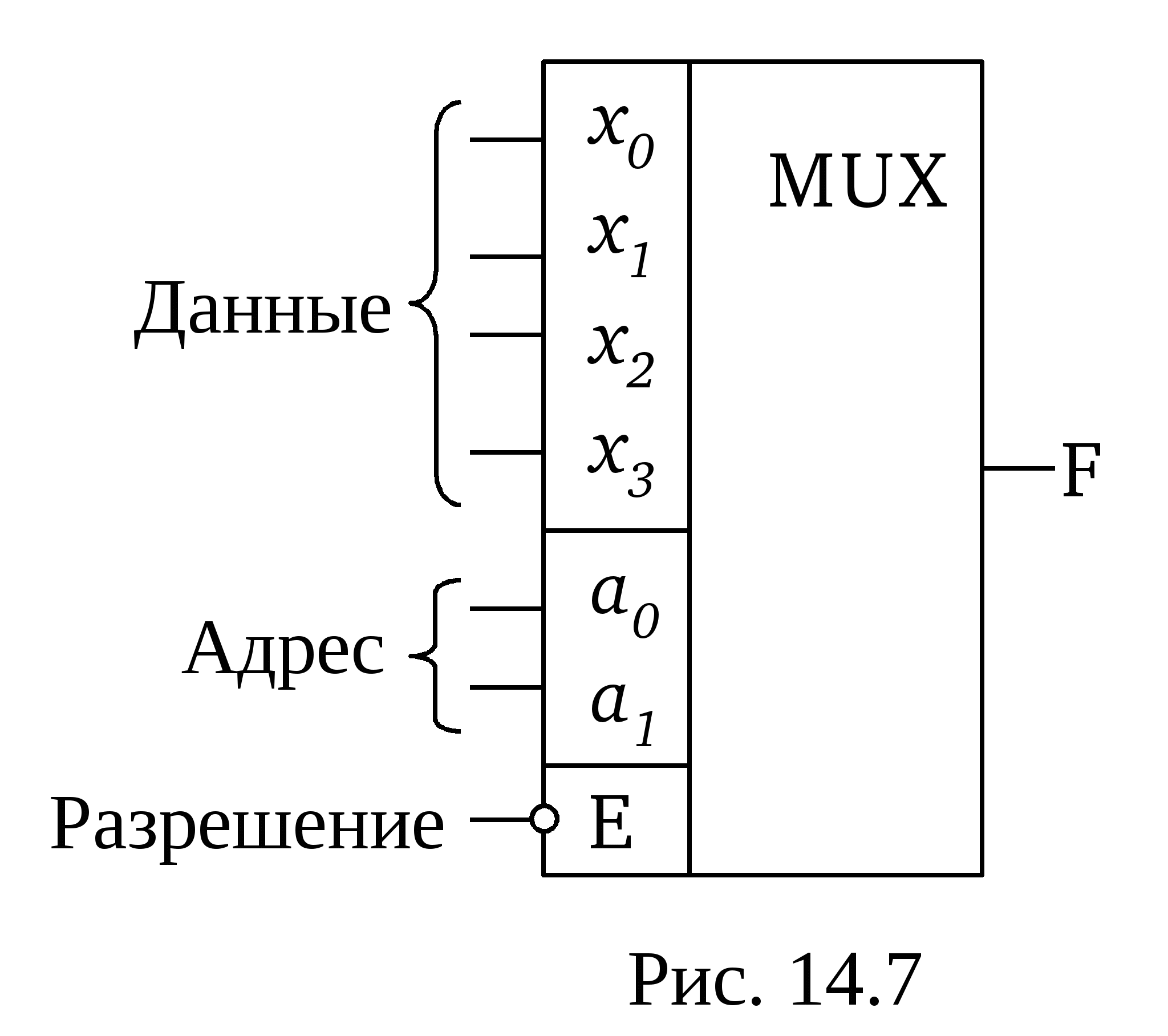 а рис. 14.7 приведено условное обозначение мультиплексора 4-1 (четыре в один, т.е. коммутирующего данные от четырех источников на одно направление). Вход  - разрешающий: при = 0 мультиплексор работает как обычно, а при = 1 его выход находится в неактивном состоянии (F=0), т.е. мультиплексор заперт. Переключательная функция (ПФ) данного мультиплексора с учетом входа разрешения имеет вид: (14.4)Один из возможных вариантов реализации этой ПФ приведен на рис. 14.8,а. Переключательную функцию (14.4) можно записать в виде:  (14.5)где :  Функции y0, y1, y2, y3 могут быть реализованы на стробируемом дешифраторе 2-4, и структурная схема мультиплексора может быть выполнена так, как показано на рис. 14.8,б. Помимо мультиплексирования сигналов (передачи их в линию друг за другом в темпе смены кодов на адресных входах) мультиплексор может осуществлять и выбор, или селекцию данных из определенного, указанного адресным кодом, источника. Поэтому за мультиплексором закрепилось и другое название - селектор. Мультиплексор иногда называют и коммутатором, поскольку он осуществляет коммутацию входных сигналов на единственный выход. Терминологичная многозначность повлекла и многозначность в условных обозначениях на функциональных схемах, на которых он обозначается MUX (мультиплексор), SL (селектор) и MS (мультиплексор-селектор). М 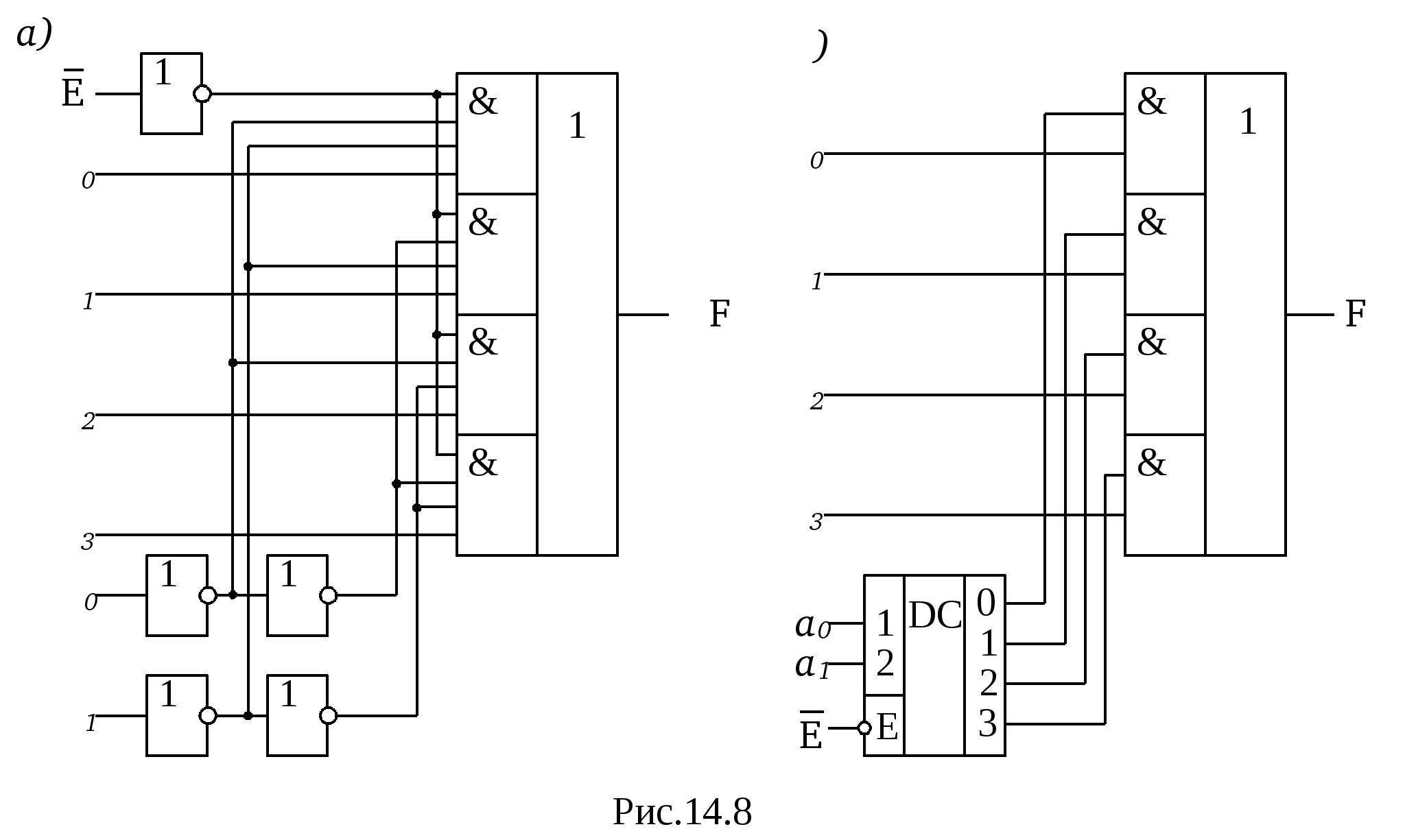 ультиплексоры 4-1, 8-1, 16-1 выпускаются в составе многих серий и имеют буквенный код КП. Их временные характеристики задаются задержками по трем трактам: вход адреса - выход, вход данных - выход, вход разрешения - выход. Для большинства серий эти задержки составляют (2…3) tзд.р.ср, где tзд.р.ср – задержка ЛЭ соответствующей серии. Другие области применения мультиплексоров П 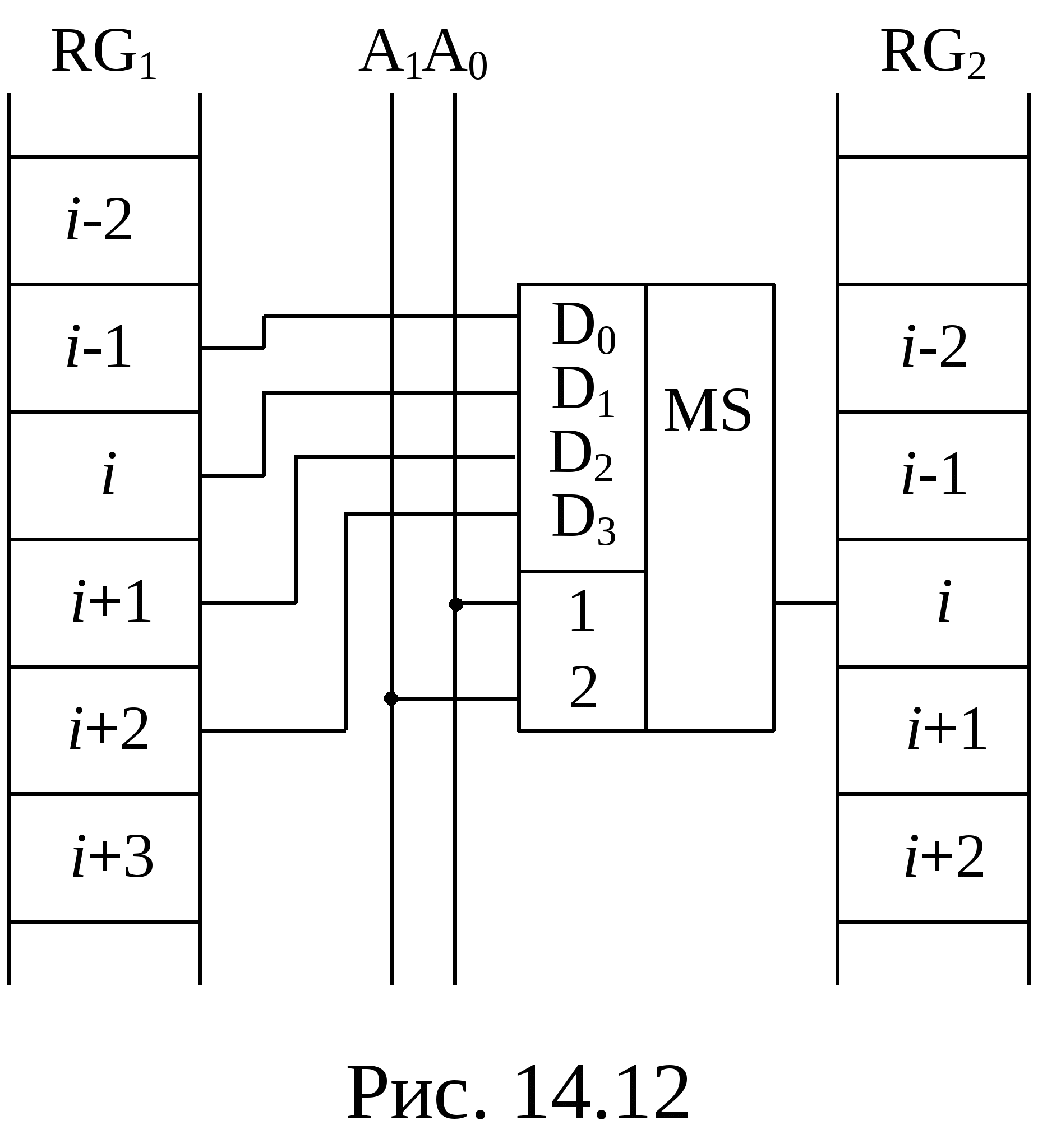 ри выполнении различных математических операций часто возникает необходимость сдвига кода числа вправо (в сторону младших разрядов) или влево (в сторону старших разрядов) на один или несколько разрядов. На рис.14.12 показан один, i-й разряд параллельного сдвигателя. В полной схеме сдвигателя ко входу каждого разряда регистра RG2 подключено по такому же мультиплексору, входы данных которого в свою очередь подключены к выходам нескольких разрядов регистра RG1. На адресные (управляющие) входы мультиплексоров всех разрядов подается один и тот же код А1А0, в зависимости от которого в i-й разряд RG2 будет переписываться содержимое различных разрядов RG1. При А1А0=01 данные регистры RG1 будут передаваться в одноименные разряды RG2 без сдвига. При коде А1А0=00 в i-й разряд регистра RG2 поступит содержимое соседнего младшего, (i-1)- разряда регистра RG1, т.е. передача информации произойдет со сдвигом на один разряд влево. При кодах А1А0=10 и А1А0=11 передача информации из регистра RG1 в регистр RG2 будет происходить со сдвигом справо соответственно на один или два разряда. Применяя мультиплексор с большим числом входов (8 – 1, 16 – 1), подключаемых к соответствующим разрядам регистра-передатчика, можно строить сдвигатели, способные очень быстро (за время, определяемое задержкой мультиплексора и регистра-приемника) сдвигать код числа в любую сторону на любое заданное число разрядов.М 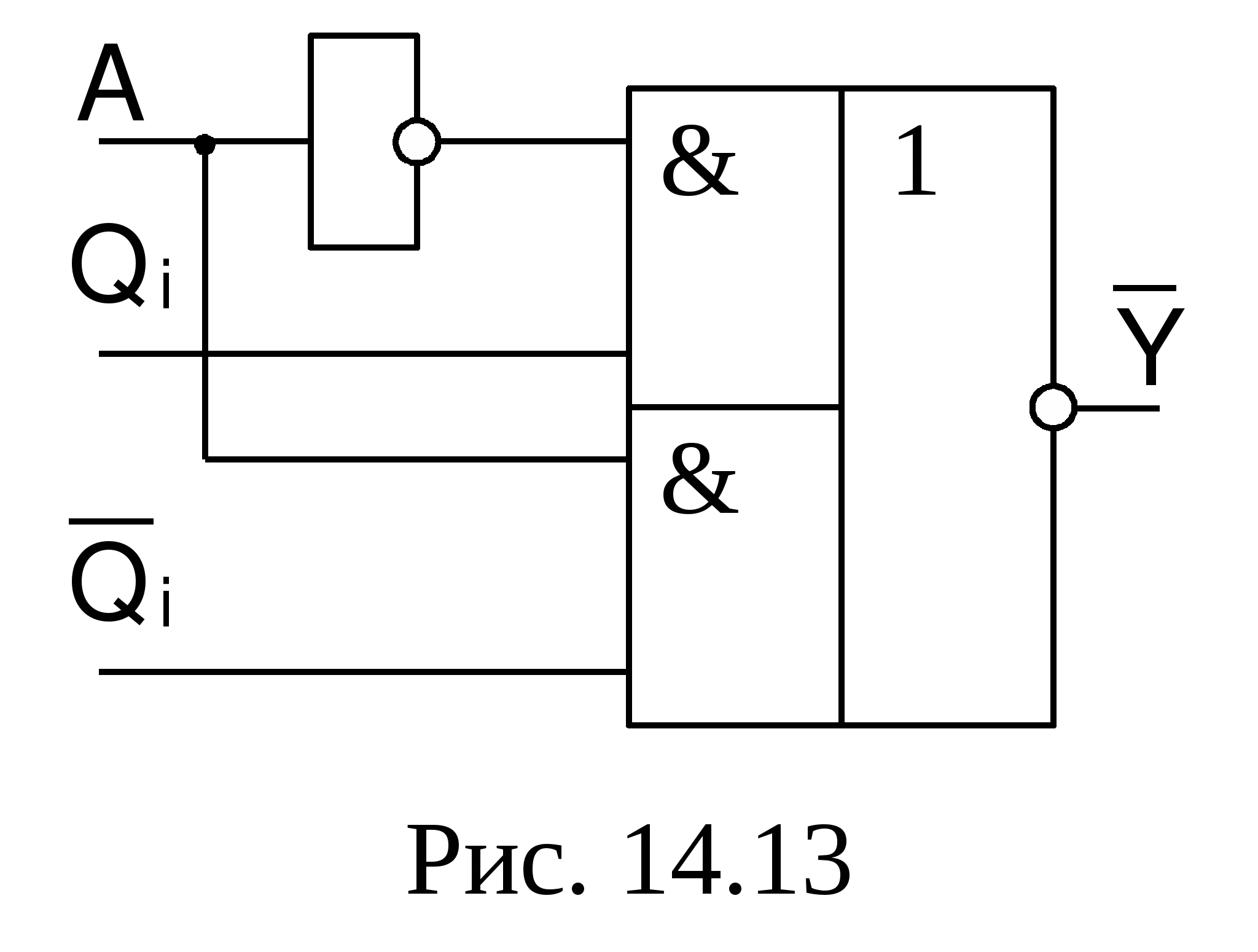 ультиплексоры удобно применять в устройствах используемых для передачи информации с регистра или другого устройства прямым или обратным кодом в зависимости от значения управляющего сигнала. С этой целью каждый разряд регистра дополняется мультиплексором 2-1, к одному входу которого подключается прямой выход разряда регистра, а ко второму – инверсный. При отсутствии мультиплексора 2-1 в используемой серии его можно построить по рис.14.13. В этом случае при А=0 на выходе мультиплексора получается обратный код сигнала от i-го разряда, а при А=1 –прямой.2  0. Мультиплексор как генератор логических функций Уравнение (14.4) для мультиплексора 4-1 без учета разрешающего сигнала  имеет вид: В этом уравнении переменные  и  представляют собой сигналы на управляющих (адресных) входах. Всегда и  могут быть выделены как множители из любой функции n переменных, после чего остаточные функции от n-2 переменных могут быть поданы на информационные входы. Например, если n=3, то при подаче на адресные входы двух переменных на информационные входы должны поступать функции третьей переменной. Если третья переменная есть х, то на информационные входы мультиплексора могут поступать сигналы  или 1 . В общей сложности существует  =256 возможных комбинаций четырех входных сигналов и мультиплексор «4-1» может сгенерировать любую из 256 возможных логических функций от трех переменных.Функции трех переменных F = f(x1, х2 , х3) соответствует карта Карно из восьми ячеек (рис. 14.10,а). Если на управляющие входы подать переменные х1, х2 , то на информационные входы возможно поступление сигналов D0, D1 D2 и D3 определяемых значениями третьей переменной х3 . При этом когда х1=0 и х2=0, то две верхние ячейки соответствуют значению D0. Значению D1 соответствуют две ячейки, у которых х1=1 и х2=0, ячейки, для которых х1=0 и х2=1 определяют значение D2, а ячейки, для которых х1=1 и х2=1- значение D3 (рис. 14.10,б). Таким образом, восьмиячеечная карта Карно для трех переменных оказалась разделенной на четыре двухъячеечные карты Карно для одной переменной, и каждой паре ячеек ставится в соответствие информационный вход. 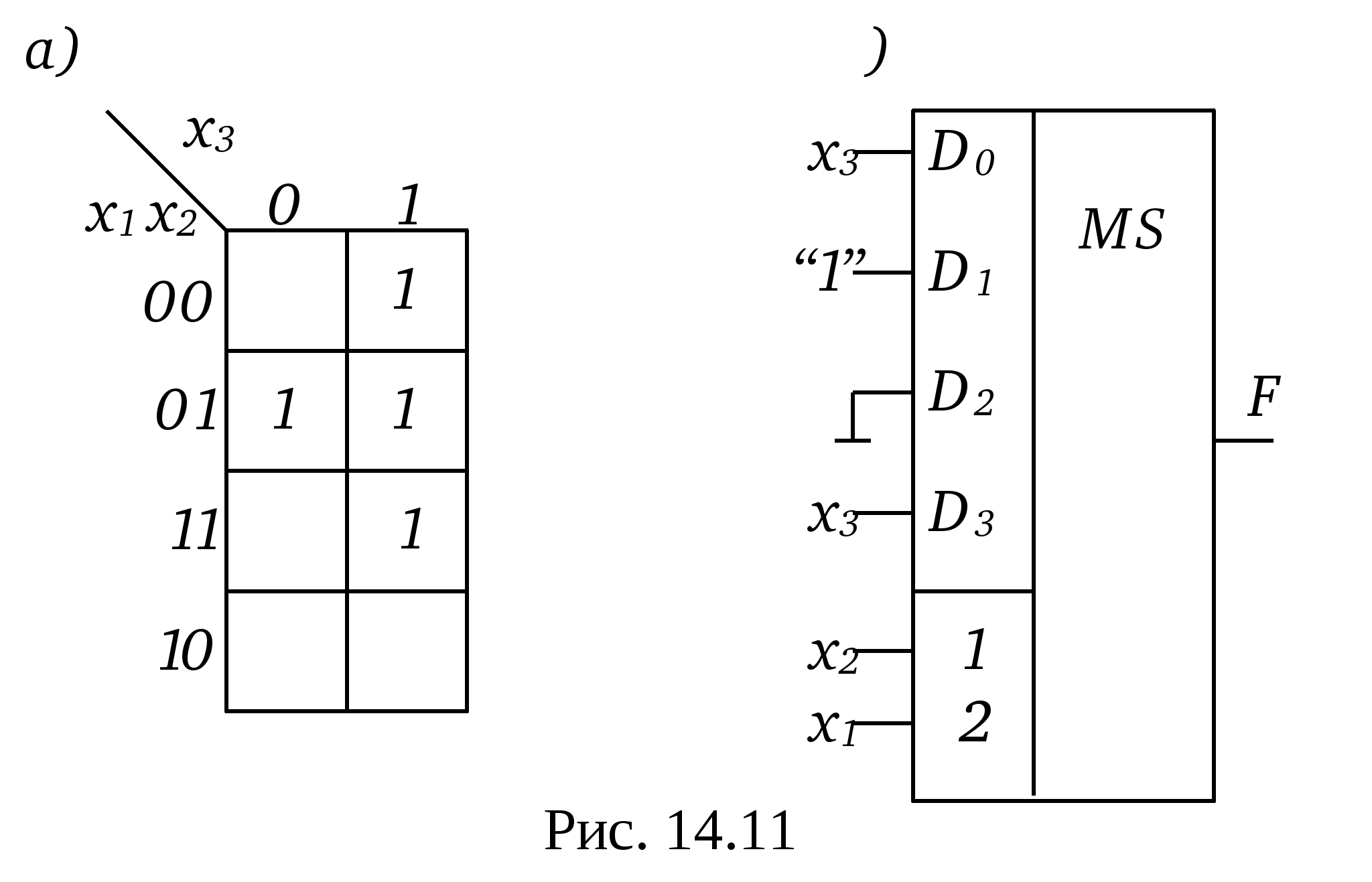 Вместо переменных х1 и х2на управляющие входы мультиплексора можно подавать переменные x1и х3 либо х2 и х3 . При подаче на управляющие входы переменных х1 и х3значения сигналов D0...D3 определятся парами ячеек, показанными на рис. 14.10,в. Если на управляющие входы подать переменные х2 и х3,то пары ячеек, определяющих сигналы D0...D3, определятся так, как показано на рис. 14.10,г. В качестве примера рассмотрим реализацию на мультиплексоре 4–1 функцию трех переменных  .Сначала эту функцию изображаем на карте Карно (рис. 14.11,а) и произвольно выбираем переменные, которые следует подать на управляющие входы мультиплексора. Пусть это будут переменные x1 и х2. Тогда сигналы D0...D3 , подаваемые на информационные входы, будут определяться парами ячеек, показанными на рис. 14.10,б. Минимизируя набор из четырех функций одной переменной х3, получим: D0 = x3, D1 = l, D2 = 0, D3 = x3. Реализация функции показана на рис. 14.11,б.Если в качестве управляющих переменных выбрать х1 и х3, то информационные сигналы D0...D3 будут определяться парами ячеек, показанными на рис. 14.10,в, минимизация которых дает: D0 = x2, D1 = l, D2 = 0, D3 = x2, а если бы управляющими переменными были x2 и х3 ,то в соответствии с рис. 14.10,г информационные сигналы имели бы следующий вид: D0=0, D1=  , D2=, D3=1. 21. Сумматоры Сумматором называют операционный узел ЭВМ, выполняющий операцию сложения двух чисел, представленных в двоичном коде. Известно, что все многообразие математических операций (сложение, вычитание, деление, возведение в степень, вычисление тригонометрических функций и т.п.) можно получить с помощью операций сложения прямых и обратных кодов чисел, сдвинутых влево или вправо на то или иное число разрядов. Поэтому скорость выполнения вычислительных процессов в ЭВМ существенно зависит от быстродействия сумматоров. По принятой в ЭВМ системе счисления и кодирования сумматоры подразделяются на двоичные, десятичные, двоично-десятичные и др. По способу организации суммирования чисел сумматоры могут быть комбинационными и накапливающими. В комбинационных сумматорах результат суммирования не запоминается. В накапливающих сумматорах, имеющих память, после добавления к содержимому сумматора очередного слагаемого происходит запоминание полученного результата. По способу организации межразрядных переносов сумматоры делятся на параллельные, последовательные и c групповой структурой. В параллельных сумматорах суммирование одноименных разрядов чисел осуществляется одновременно (параллельно), а в последовательных — последовательно от младших к старшим. В сумматорах с групповой структурой суммируемые числа разбиваются на группы, построенные как параллельные сумматоры, а полученные в группах переносы складываются затем последовательно (параллельно-последовательные сумматоры) или параллельно. В последнем случае сумматоры называют параллельными с параллельно-параллельным переносом. По способу тактирования различают синхронные и асинхронные сумматоры. В синхронных сумматорах для выполнения процесса суммирования отводится постоянное время независимо от разрядности суммируемых чисел, а в асинхронных после завершения процесса суммирования вырабатывается специальный сигнал (признак). Поэтому у асинхронных сумматоров среднее время суммирования меньше, чем у синхронных. Одноразрядные двоичные сумматоры В ЦВМ применяются одноразрядные двоичные сумматоры на два и три входа. Первые называются полусумматорами, вторые — полными одноразрядными сумматорами (ПОС). Работа полусумматора определяется табл. 15.1, из которой видно, что полусумматор должен иметь два выхода: s0 — выход частичной суммы и c1 —выход сигнала переноса. Логические функции по выходам s0 и c1 , полученные на основании этой таблицы, имеют вид:   (15.1)Реализованная по этим выражениям схема и ее УГО показаны на рис. 15.1а, б.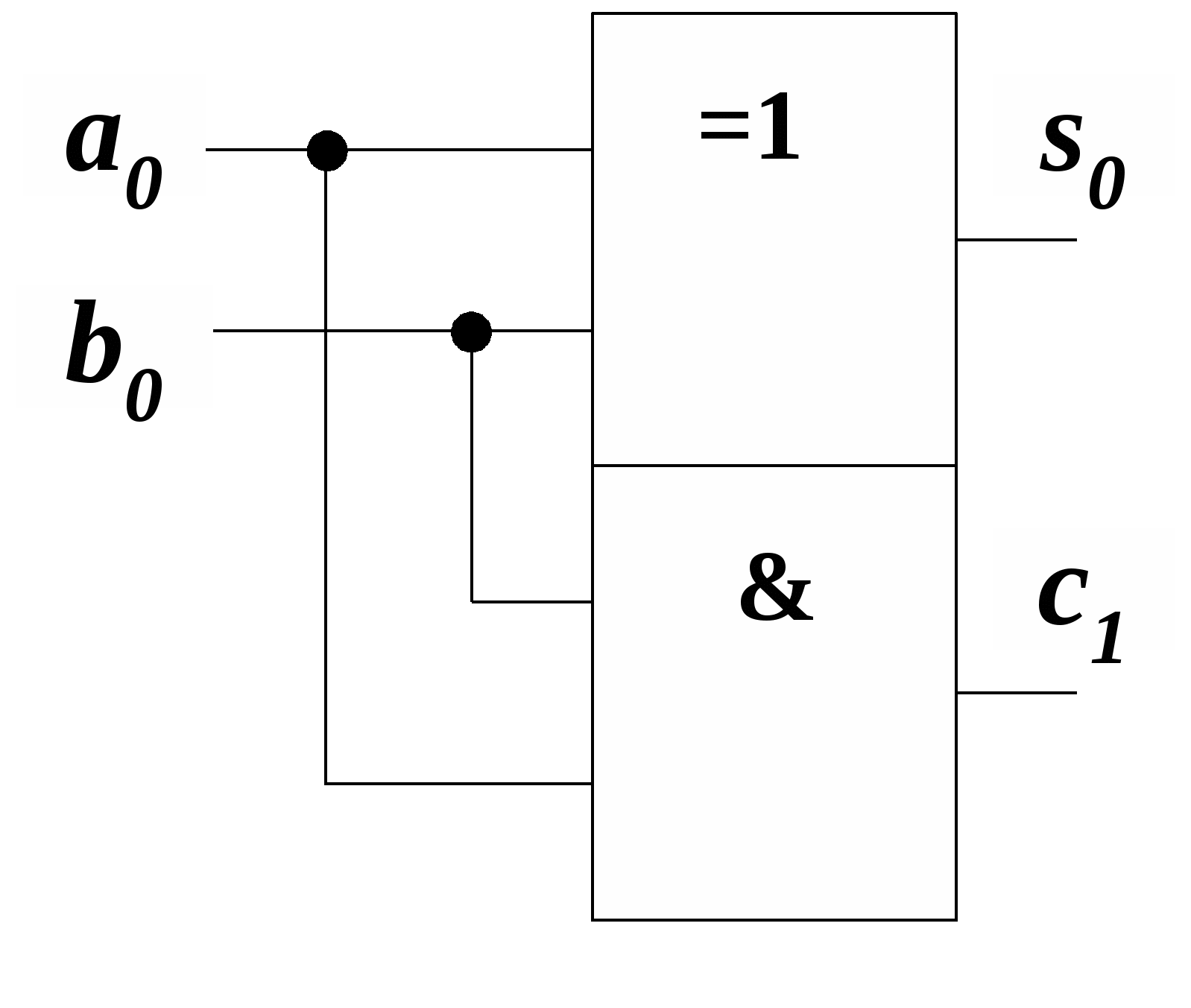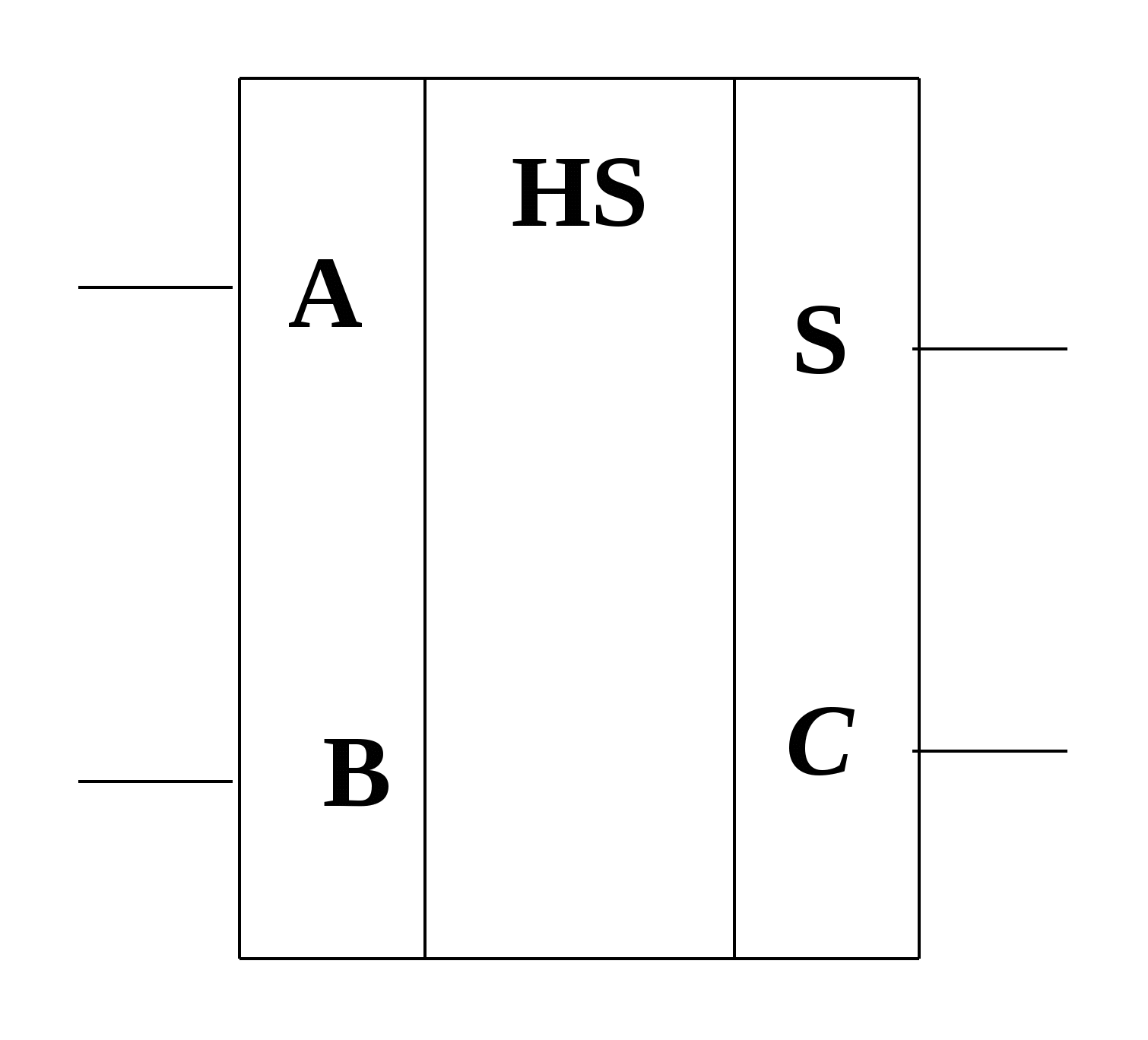    
Рис. 15.1 Входящий в нее элемент “ИСКЛЮЧАЮЩЕЕ ИЛИ” называют “сумматором по модулю 2” по той причине, что его выходная функция соответствует значению младшего разряда при суммировании двух одноразрядных двоичных чисел. На рис. 15.2 показаны варианты реализации сумматора по модулю 2 в различных базисах: И, ИЛИ, НЕ (рис.15.2, а), И-НЕ (рис. 15.2, б) и ИЛИ-НЕ (рис.15.2, в). Из рисунка видно, что минимальная задержка формирования выходов функции s0 составит 3tзд.р.ср, где tзд.р.ср — среднее время задержки распространения сигнала в одном ЛЭ. Из рис. 15.2, а, б, в также следует, что для реализации сумматора по модулю 2 в том или ином базисе потребуется не менее 5 ЛЭ, а полусумматора (с учетом формирования переноса с1) — не менее 7 ЛЭ. Из этого следует, что синтез полусумматора на основании соотношений (15.1) и (15.2) оказывается нерациональным. И (15.3, а) зобразим функцию (15.1) таким образом, чтобы в нее входили только п  рямые переменные a0 и b0: Д  (15.3, б) ля реализации в базисе И-НЕ функция (15.3,а) преобразуется к виду: 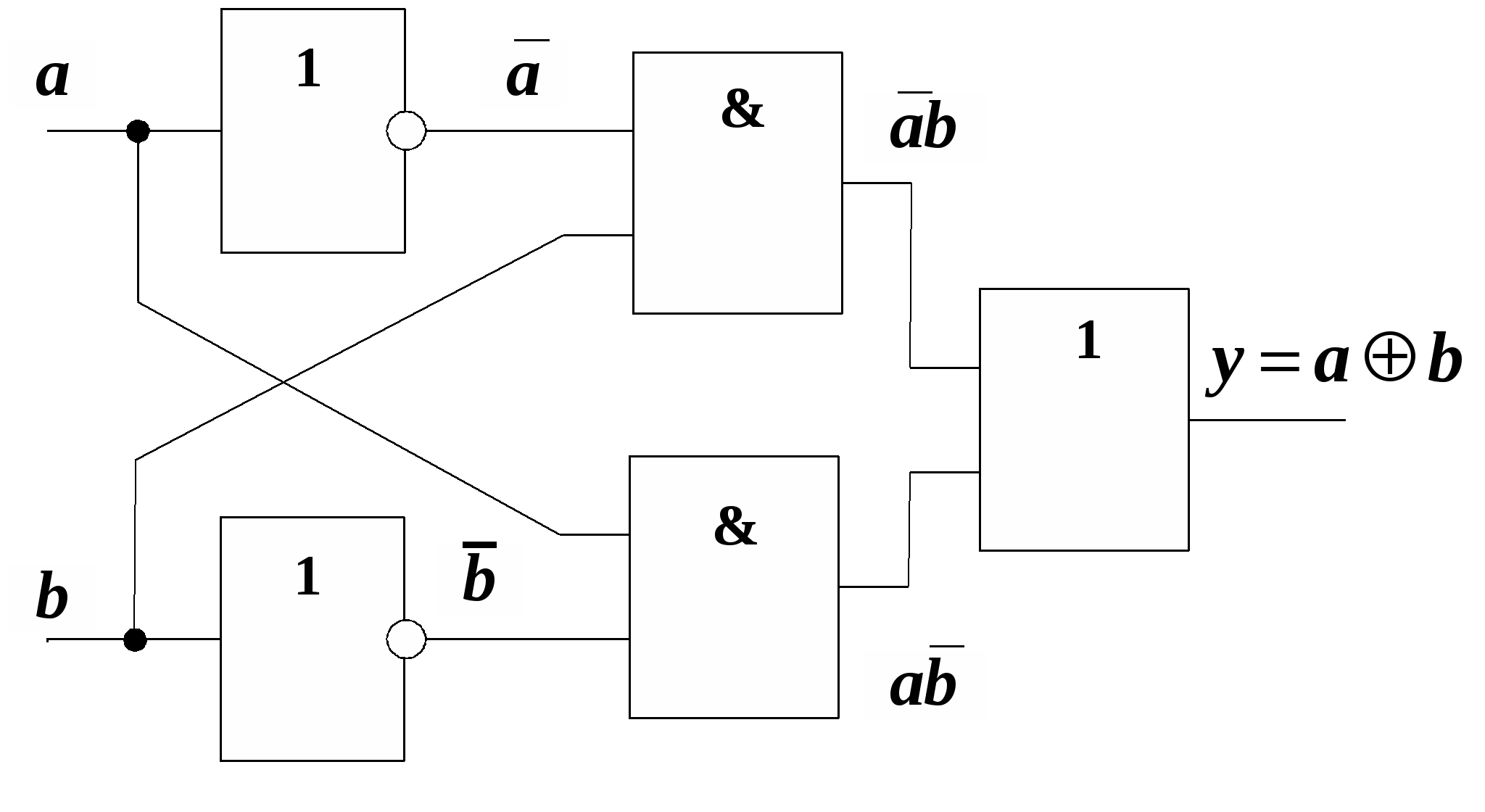 а) 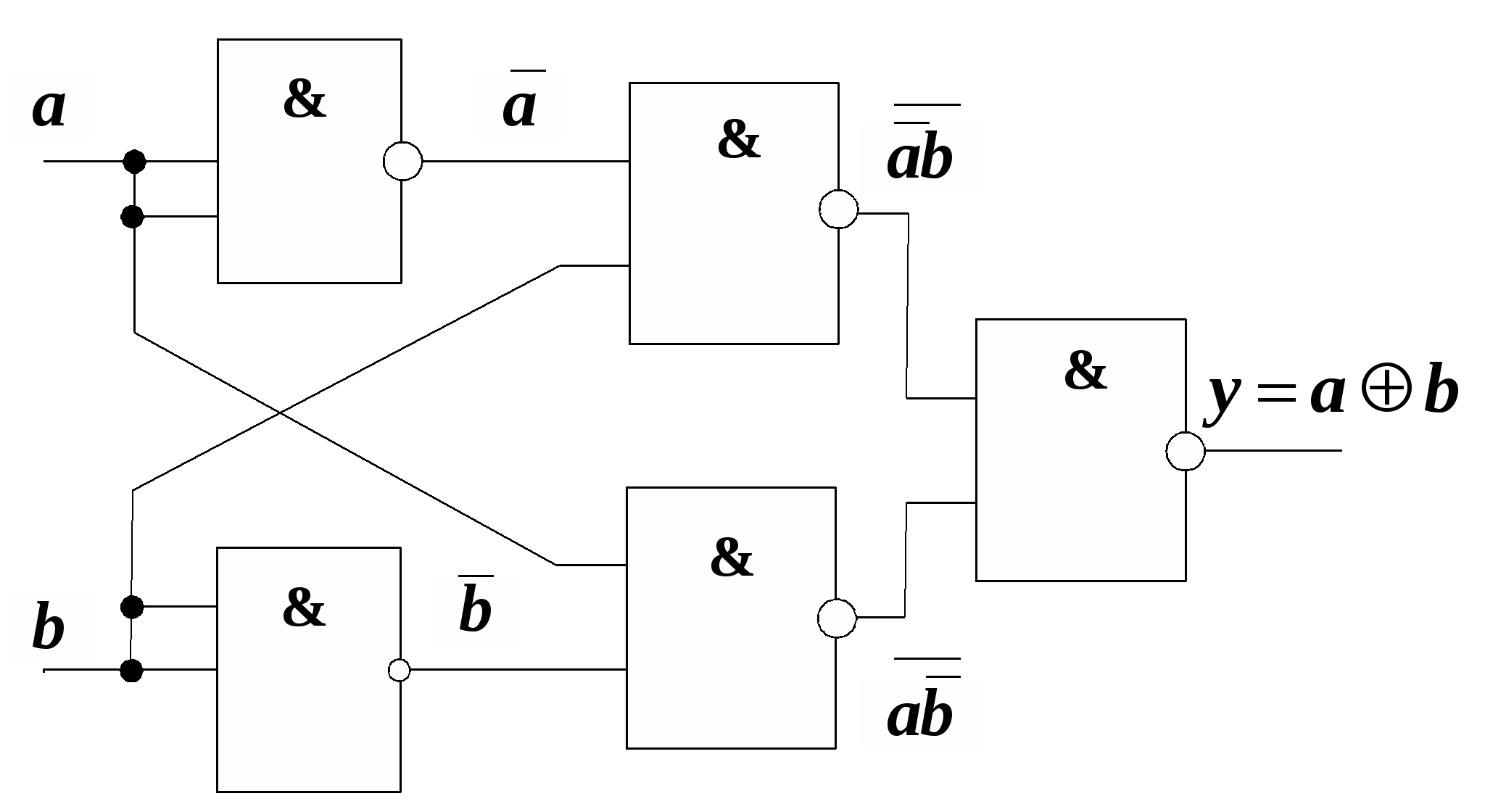 б) в) 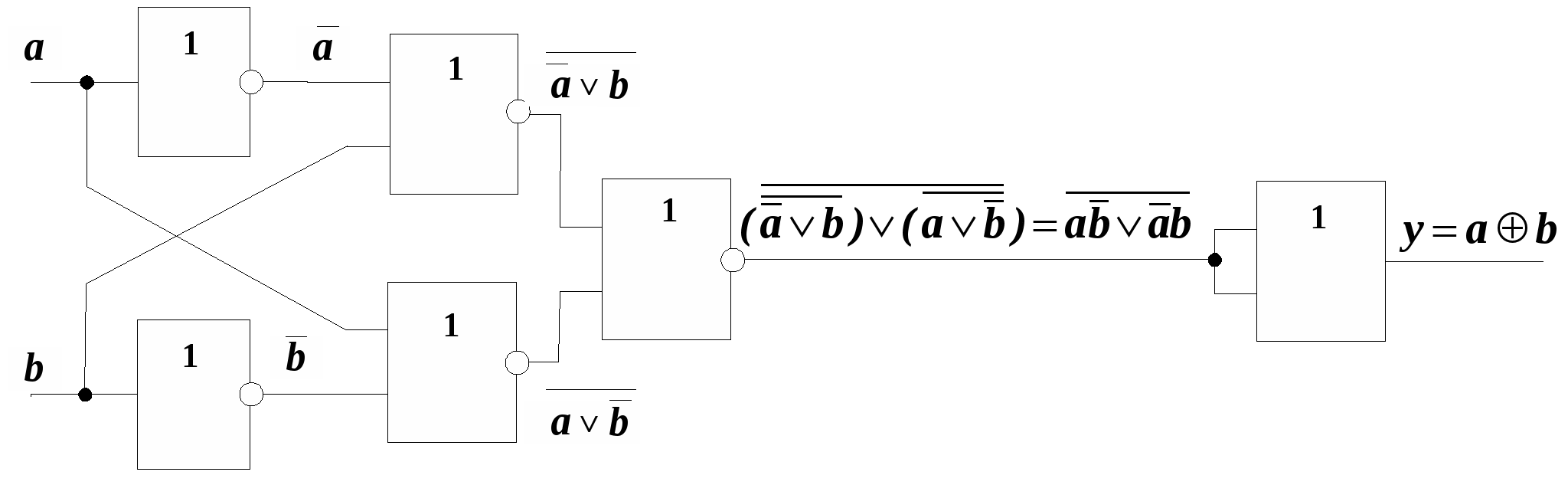 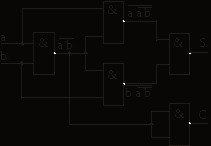 22. Полный одноразрядный сумматор В общих случаях работа ПОС определяется табл. 15.2, из которой следует: 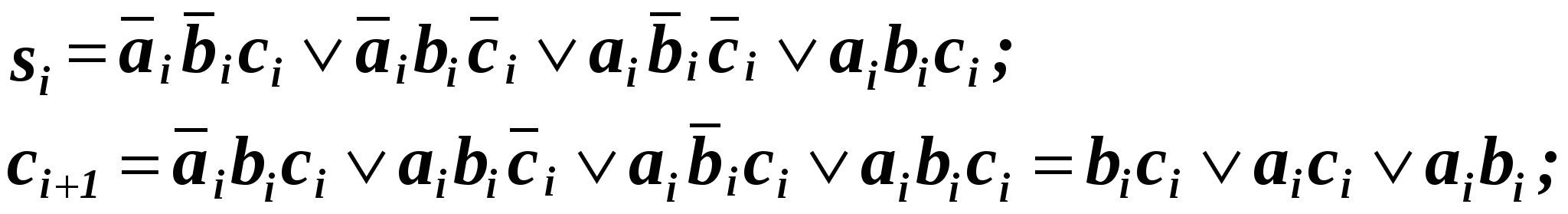 Таблица 15.2  Уравнения (15.4) и (15.5) можно преобразовать следующим образом :  (15.6) (15.7)Схема ПОС, построенная на основании уравнений (15.6) и (15.7), показана на рис. 15.3, а, а на рис. 15.3, б дано его условное обозначение. Недостатком такой схемы является большое время задержки формирования частичной суммы si (tсумм=6 tзд. р. ср ). 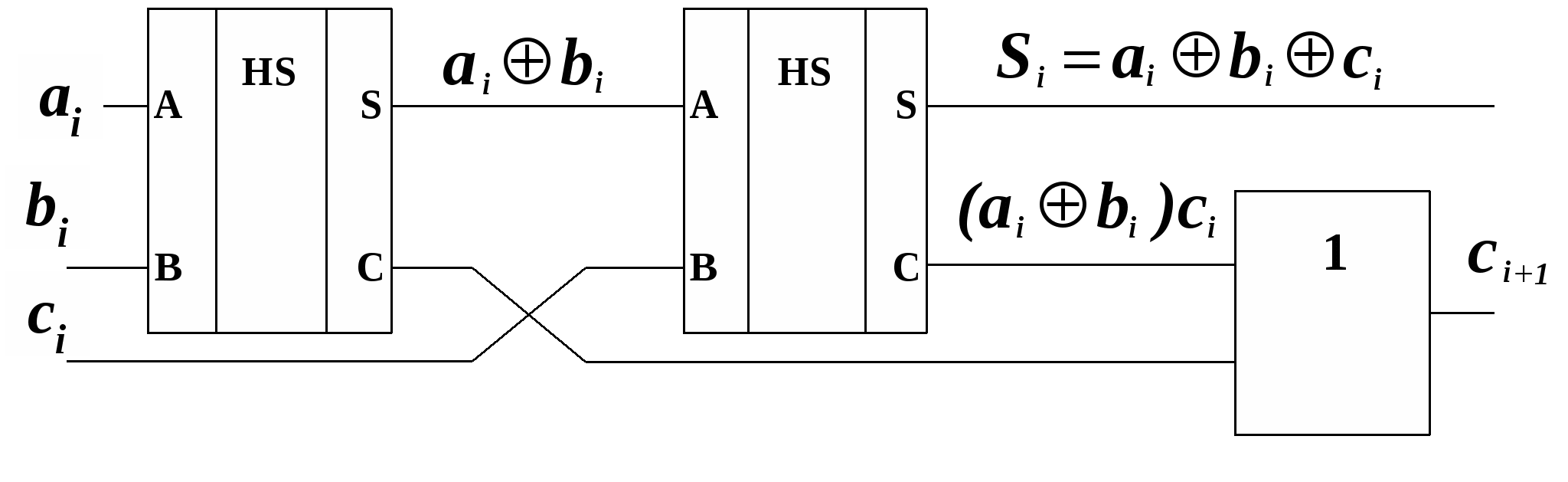  б) а) Рис. 15.3 Схему быстродействующего ПОС можно построить непосредственно по уравнениям (15.4) и (15.5), используя базис И-ИЛИ (рис.15.4, а). Недостатком этой схемы является необходимость ввода суммируемых чисел в парафазном коде либо включения дополнительных инверторов на входах ai , bi, ci. Можно построить и более экономичные схемы ПОС. Для этого необходимо преобразовать функцию si таким образом, чтобы в нее входила функция ci+1или ее инверсия, т.е. считать функцию si функцией не трех, а четырех переменных s i = f (ai , bi , ci , ci+1). а) б) Таблица 15.3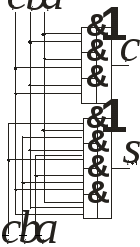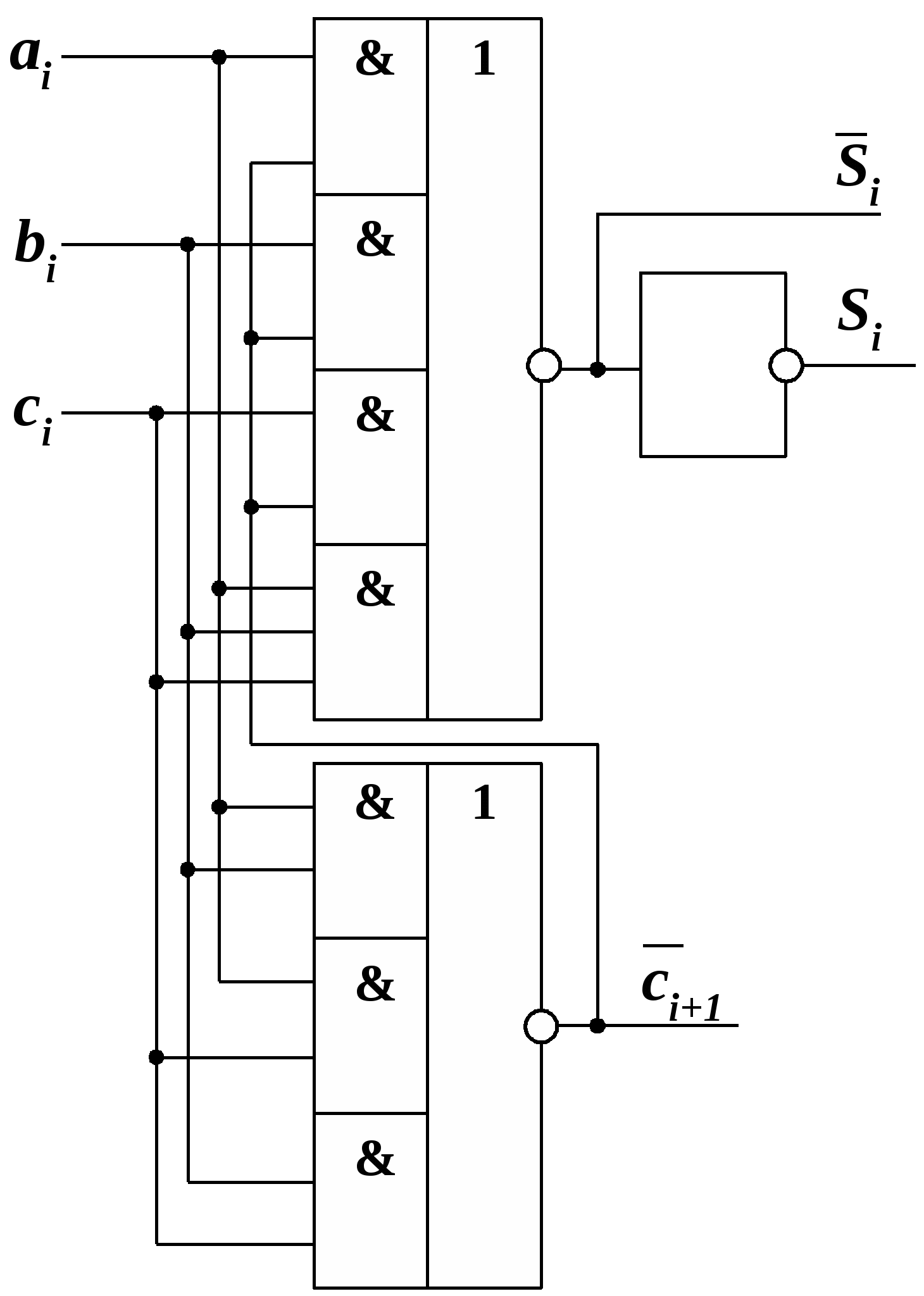  
Рис. 15.4 Значения этой функции при различных значениях переменных отображены в табл.15.3, причем, в этой таблице знаком «*» обозначены избыточные комбинации, которые не могут встретиться при работе сумматора . Минимизируя функцию с помощью диаграммы Вейча, получим:  . (15.8)Схема ПОС, построенная на основании уравнений (15.5) и (15.8) в базисе И-ИЛИ-НЕ, приведена на рис.15.4,б. В этой схеме выход переноса инверсный, частичная сумма реализуется как в прямом, так и инверсном виде. Такое выполнение ПОС упрощает построение многоразрядных сумматоров за счет использования свойств самодвойственности функций переноса и частичной суммы. Самодвойственными называются такие функции, инвертирование аргументов которых приводит к инвертированию самих функций, т.е. если вектор аргументов обозначить через X , то можно записать:  Свойство самодвойственности функций si и ci+1 наглядно отражено в табл. 15.2, в которой прямоугольными скобками объединены строки, отличающиеся между собой инвертированием аргументов. 23. Многоразрядные последовательные сумматоры Многоразрядный последовательный сумматор содержит полный одноразрядный сумматор (ПОС), три сдвиговых регистра и синхронный D-триггер (рис. 15.7). Для суммирования двух чисел, представленных в двоичных кодах, они предварительно записываются в регистр числа А и регистр числа В. Если регистры 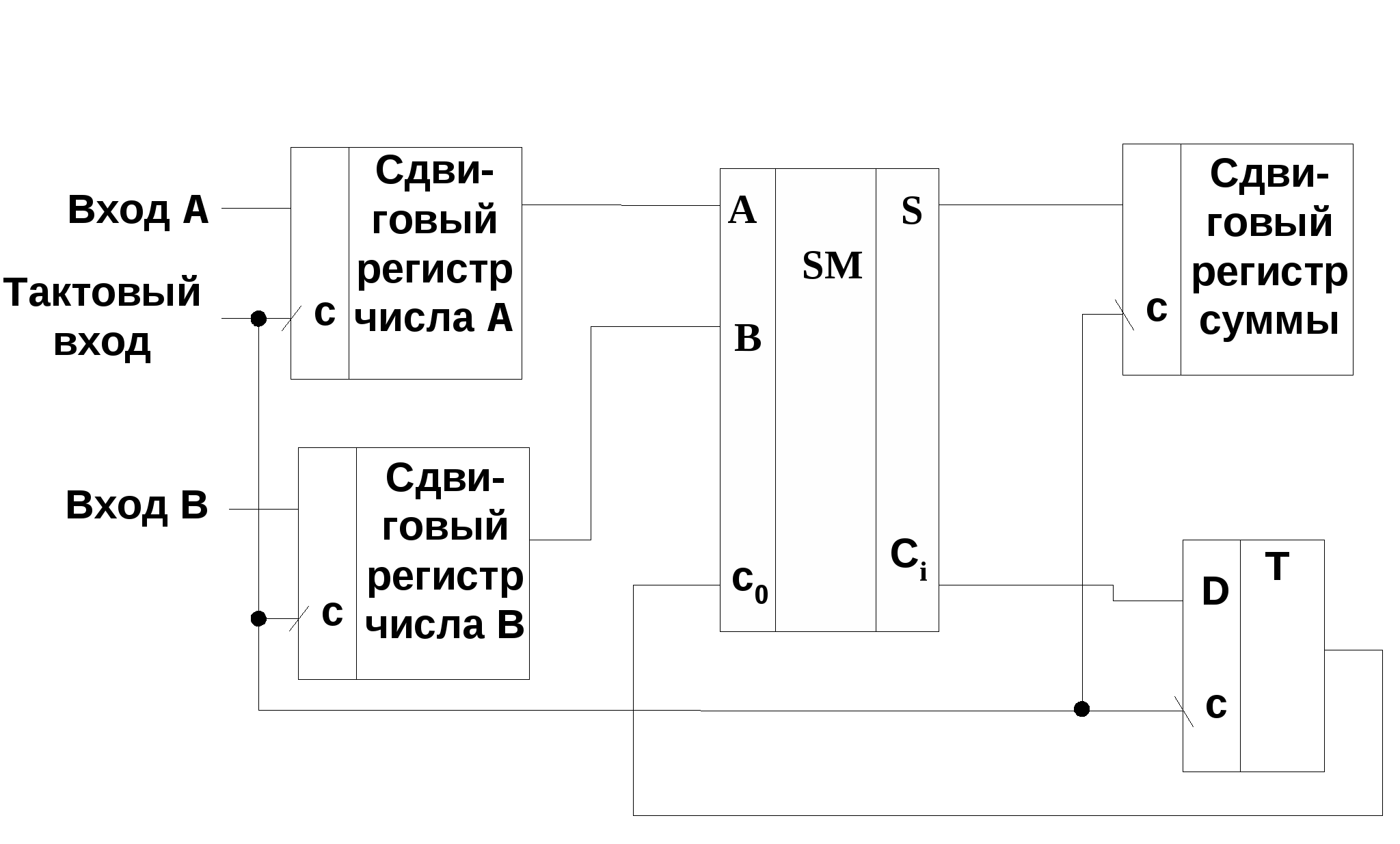 Рис.15.7
С приходом первого положительного тактового импульса открываются выходные конъюнкторы регистров чисел А и В и на входы ПОС поступают значения младших разрядов этих регистров Q0 = 0. Поскольку при этом перенос не возникает, то на входе D триггера образуется сигнал логического 0. По окончании первого тактового импульса его отрицательным фронтом значение полученной частичной суммы, определяемое первоначальным состоянием D-триггера, запишется в старший разряд n-разрядного сдвигового регистра суммы, а D-триггер установится в нулевое состояние. С приходом второго положительного тактового импульса на входы сумматора поступят разряды a0 и b0 суммируемых чисел и сигнал переноса c0=0, по которым будут вычислены значение частичной суммы s0 и перенос c1 в первый разряд. По отрицательному фронту тактового импульса эти значения будут переписаны в сдвиговый регистр суммы и D-триггер. Одновременно с этим прервутся связи регистров чисел А и В с ПОС. С приходом третьего тактового импульса на входы А и В ПОС поступят разряды a1 и b1 слагаемых и перенос c1, полученный в предыдущем такте. После (n+1)-го импульса в сдвиговом регистре суммы будет записан результат суммирования двух n-разрядных чисел, а состояние D-триггера определит сигнал переноса в (n+1)-ый разряд. Время суммирования в таком сумматоре с учетом операции обнуления D-триггера составляет tсумм = (n+1)T, где T – длительность периода тактовых импульсов. При этом длительность положительных тактовых импульсов должна быть не менее времени суммирования ПОС. 24. Многоразрядные параллельные сумматоры Параллельные многоразрядные сумматоры строятся на основе ПОС. На рис. 15.8 приведена схема параллельного n-разрядного сумматора с последовательным переносом, составленного из одноразрядных сумматоров. Правильные значения 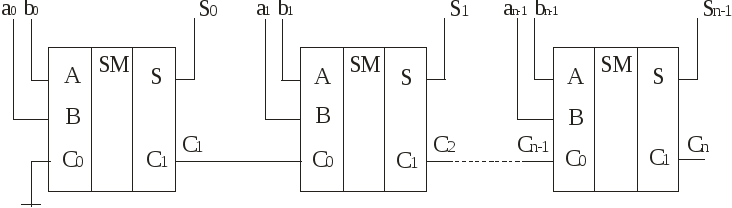 Рис.15.8 частичных сумм S0 … Sn-1 будут устанавливаться последовательно, начиная с младшего разряда. Самым последним устанавливается правильное значение частичной суммы Sn-1. Максимальное время суммирования в таком сумматоре составляет:  . (15.9)Примером интегрального параллельного сумматора с последовательным переносом является микросхема К564ИМ1. Это - четырёхразрядный сумматор, выполненный по КМДП-технологии. Его структурная схема и УГО показаны соответственно на рис.15.9,а и 15.9,б. Он отличается от схемы рис.15.8 наличием схемы ускоренного формирования выходного переноса c4 (подробно такая схема рассмотрена в п.15.1.4), подаваемого на вход переноса следующей микросхемы при наращивании разрядности. Благодаря наличию такой схемы удаётся увеличить быстродействие многоразрядных параллельных сумматоров с последовательным переносом. При напряжении источника питания Uп =10 В время задержки по трактам от входа c0 до выхода переноса c4 и от входов слагаемых младших разрядов до выхода суммы старшего разряда составляет 140 нc. При Uп = 5 В задержка сигналов увеличивается до 300 нc. 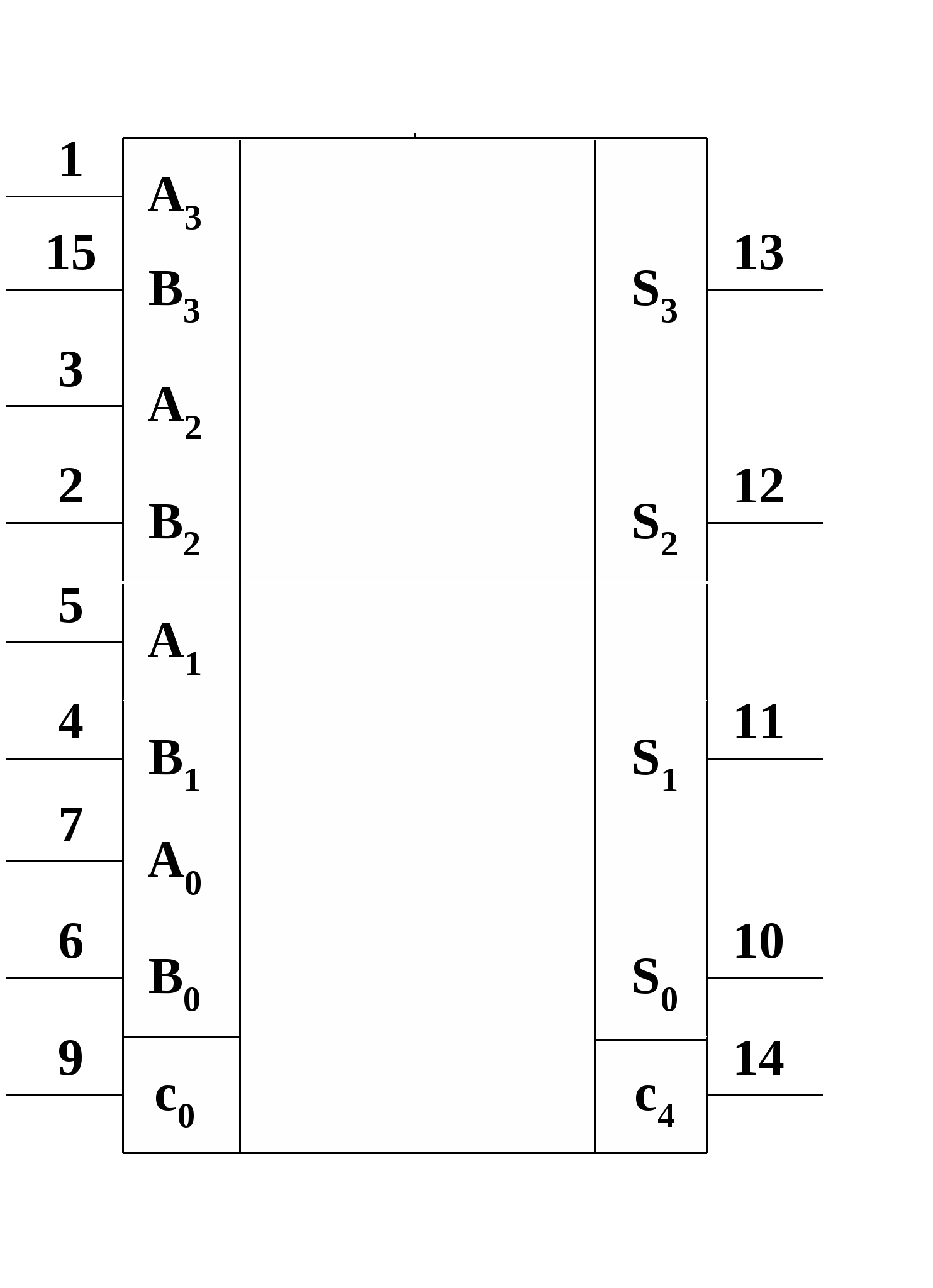 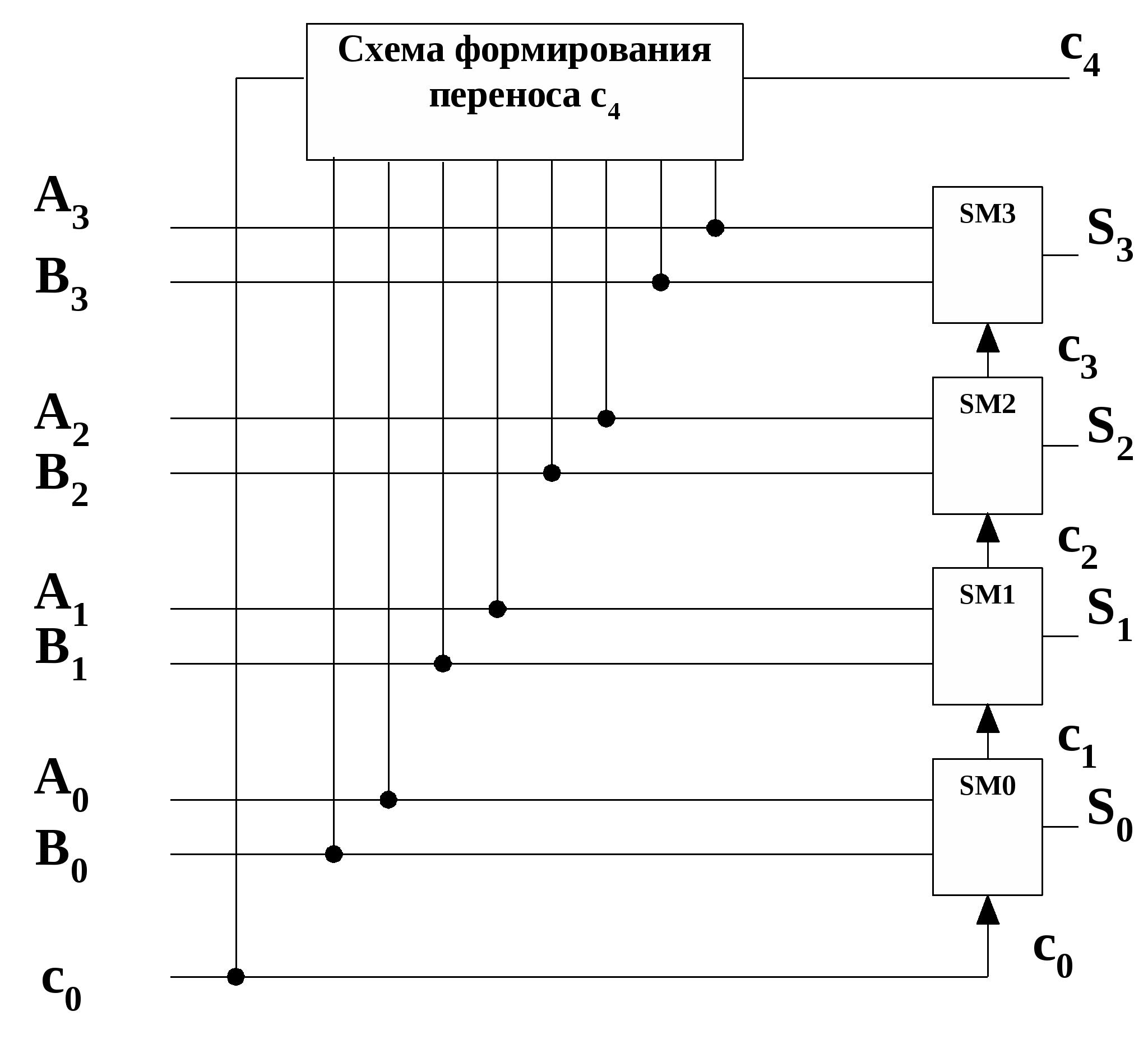 |