вариант6. 1. Сформулировать содержательную часть работы
 Скачать 344.5 Kb. Скачать 344.5 Kb.
|
|
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.…………..……………………………………………………..........3 1. Сформулировать содержательную часть работы …………………………........4 2. Сформулировать выборку из задания…………………………………………...8 2.1. Среднее значение……………………………………………………….8 2.2. Дисперсия и среднее отклонение……………………………………...8 2.3. Отсев грубых ошибок……………………………..……………………8 2.4. Законы распределения случайной величины........................................9 2.5. Нормальный закон распределения случайной величины…………..11 2.6. Доверительный интервал……………………………………………..12 2.7. Математическая модель……………………………………………....12 Заключение ……………………………………………………...………………..13 Библиографический список…………………………………………………….. 14 ВВЕДЕНИЕ Объекты исследований по любому из направлений, как правило, сложны и связаны со значительным количеством как управляемых, так и неуправляемых (независимых) факторов. На параметры их состояния могут существенно влиять элементы случайностей, имеющих сложную природу происхождения. Для установления закономерностей функционирования этих объектов в реальных условиях одних теоретических исследований недостаточно, так как аналитически описать изучаемый объект с достаточной точностью не всегда представляется возможным. Такие объекты характерны практически всем направлениям прикладных исследований, как в технологии, так и в технике и в области естественных наук. Экспериментальные данные могут быть использованы для проверки и уточнения рабочих гипотез, а также обоснования направления исследований в соответствующей области. Эффективность исследований в целом повышается, если теоретические предпосылки уточняются опытным путем, а экспериментальные данные анализируются и обобщаются на базе теоретических положений соответствующих отраслей наук.
Деталь изготавливают из стали 35Л ГОСТ 977-88 обычного качества, то деталь не испытывает значительных механических нагрузок и имеет достаточно несложную конфигурацию. Проанализировав чертеж детали можно сказать, что конструкция ее достаточно технологична для изготовления литьем. Деталь не имеет резких переходов толщин и конфигурации стенок, наружная поверхность проста в геометрии, деталь выполняет свою функциональную роль в узле, при этом обладает комплексом эксплуатационных свойств (прочностью, надежностью и т.д.). Технологические требования: * формовочные уклоны по ГОСТ 3212-92 * точность отливки 6-7-13-7 по ГОСТ Р 53464-2009 * литейная усадка 2%. 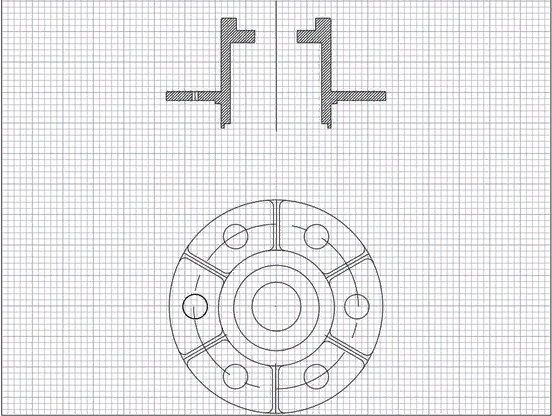 В технических условиях чертежа заданы класс размерной точности 8 и класс точности масс 7, определим степень коробления и степень точности поверхности необходимо задать с помощью табл. 1.9 (табл. Б.1 приложения Б ГОСТ Р 53464-2009) и из табл. 1.13( табл.В.1 приложения В ГОСТ Р 53464-2009) соответственно. Отношение наименьшего размера элемента к наибольшему в данной отливке составляет 0,028. Отливка из стали изготавливается в разовую форму и подвергается термообработке и ее степень коробления равна 7. Степень точности поверхности задаем, исходя из способа изготовления литейных форм (литье в песчано-глинистые сырые формы), наибольшего габаритного размера отливки 350 мм и термообрабатываемого стального сплава. В условиях массового производства и средней сложности отливки, степень точности поверхности составляет 13. Таким образом, точность отливки 6-7-13-7 ГОСТ Р 53464-2009. Основной допуск для 6 класса размерной точности для цилиндрических и плоских торцевых поверхностей составляет 0,9мм. Допуск формы поверхностей для 7 степени коробления 0,4 мм. Допуск неровностей поверхности для 12 степени поверхности составляет 0,64 мм. Общий допуск 2,14. Учитывая рекомендации табл.1.11 (табл. И.1 приложения И ГОСТ Р 53464-2009), для допуска размера 1,1 мм допуска формы и расположения поверхности 0,4 мм общий допуск элемента отливки должен быть не более 1,4 мм. В зависимости от степени точности поверхности определяем также ряд припуска на механическую обработку по табл. 4.1( табл. Е.1 приложения Е ГОСТ Р 53464-2009). Учитывая шероховатость обработанной поверхности, заданной на чертеже детали, определяем вид механической обработки по табл.4.3- чистовая. Отливка изготавливается в песчано-глинистой форме. Модели выполняются из алюминиевого сплава АК-12 (ГОСТ 1583-93). Формовочные уклоны, в соответствии с ГОСТ 3212-92, для отливки «шкиф», в зависимости от высоты формообразующей поверхности, составляет от 1̊10’. Для определения объема прибылей применим методику Й. Пржибыла. Объем прибыли согласно этой методике вычисляется по формуле: 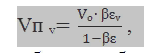 где β− отношение объема прибыли к объему усадочной раковины, для закрытой прибыли, работающей под давлением меньше атмосферного β= 10; εᵥ- часть объемной усадки, участвующая в образовании усадочной раковины, для углеродистой стали εᵥ= 0,045; Vₒ- объем питаемого узла. Объем питаемого узла составляет 1331,5 см3. По Пржибыла найдем объем прибыли: Vприб = 1331,5 * (10*0,045\10-10*0,045)=1089,449 см3 Наиболее экономичными способами подвода металла в полость формы и простым является подводом металла по разъему. Для определения форм из чайников ковша. Оптимальную продолжительность заливки формы определим по формуле: 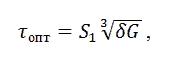 где ��опт− оптимальная продолжительность заливки, с; ��1− коэффициент продолжительности заливки, зависящий от температуры заливки, рода сплава, места подвода, материала формы и ряд других факторов; ��− преобладающая толщина стенки отливки, мм; G- масса жидкого металла, приходящегося на одну отливку в форме, кг. Вычислим массу жидкого металла: где ��отл− масса отливки; ��пр− масса прибыли, вычисляемая по формуле: ��пр=��пр∙��ме=7,8*1089,44=8.38кг ��л.с.− масса литниковой системы (примем 8% от массы отливки) G= 8,38+1,73+21,66=31,77 кг 2. Сформулировать выборку из задания 2.1. Среднее значение Рассчитаем среднее значение по формуле 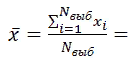 где ��выб – количество измерения; ���� – значение измерения. 2.2. Дисперсия и среднее отклонение Дисперсия - мера разброса случайной величины, то есть ее отклонения от математического ожидания. ��2=∑(����−��̅)��выб��\1��выб=0,0046 (2) Стандартное отклонение - оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии. ��=√��2= 0,067 (3) 2.3. Отсев грубых ошибок Исключение грубых ошибок проводится с использованием критерия Граббса. Для этого вычисляют критерии Граббса, предполагая, что наибольший или наименьший результат измерений вызван грубыми погрешностями.
(4)
(5) Где ��1 и ��2 критерии Граббса для наибольшего и наименьшего результатов измерения. ��������,��������- наименьший и наибольший результат измерений (0,15 и -0,45). Сравнивая G1 и G2 с теоретическим значением критерия Граббса Gt=3,286, при выбранном уровне значимости q=3% (Таблица критериев Граббса приведена в ГОСТ Р 8.736-2011.), делаем вывод что ��������,�������� не являются промахом , так как G1 Следовательно, грубых ошибок в исследуемой выборке нет. 2.4. Законы распределения случайной величины Переменная величина называется случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями. Наиболее полной, исчерпывающей характеристикой случайной величины является закон распределения. Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина x принимает определенное значение ���� или попадает в некоторый интервал. Если случайная величина имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения. Зависимость частот nx/n от интервалов определяет эмпирическое распределение вероятностей случайной величины x, графическое представление которой называется гистограммой. Чтобы узнать какой диаметр встречается чаще всего, построим гистограмму (рисунок 2). 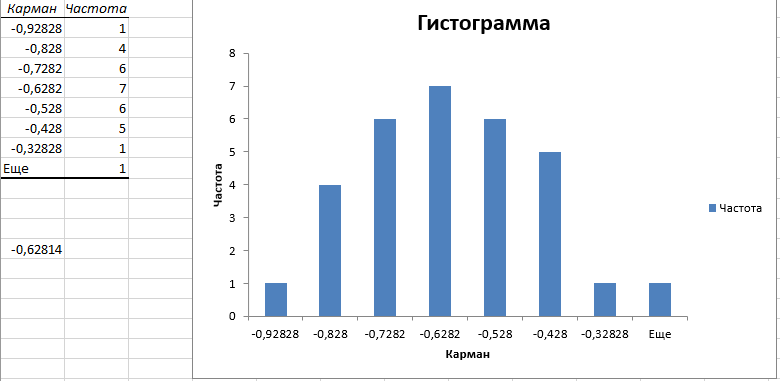 Как видно из гистограммы (рисунок 2) мы получили куполообразную зависимость, это свидетельствует о том, что наименьшие отклонения от среднего значения встречаются намного чаще, чем большие отклонения. 2.5. Нормальный закон распределения случайной величины. Нормальным законом называют распределение случайной величины, которая может принимать любые значения в интервале (a,b), причем вероятность попадания ее в любой отрезок внутри (a,b) пропорциональна длине отрезка и не зависит от его положения, а вероятность значений вне (a,b) равна 0. 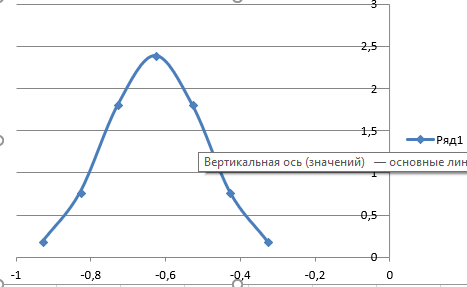 2.6. Доверительный интервал Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине), вы получите при повторении измерений (эксперимента). Для того чтобы проверить, входит ли наш показатель в доверительный интервал, определяется двухсторонний доверительный интервал для среднеарифметического значения по формуле: 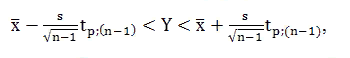 где tp;(n−1) – критерий Стьюдента при доверительной вероятности p и числе степеней свободы (n - 1) (tp;(n−1) 2,286380229); Y – квантиль случайной величины. Для расчета коэффициента Стьюдента используем в «Exel» функцию СТЬЮДРАСПОБР (α, КСС), где α = 0,03 (вероятность), КСС = 34 (степень свободы). КСС = N – 1; КСС=35-1=34, 21,40937 ≤ 21,46677 ≤ 21,52418 Полученное среднее значение отношения предела текучести к временному сопротивлению входит в доверительный интервал. Можно утверждать, что грубые ошибки отсутствуют. 2.7. Математическая модель Представим математическую модель процесса в виде зависимости плотности распределения случайной величины от измеряемых значений  ЗАКЛЮЧЕНИЕ В курсовой работе разработан технологический процесс изготовления отливки «Шкиф» из стали марки 35Л ГОСТ 977-88 в соответствии с техническими требованиями на литую деталь. В ходе работы был проведен анализ данных значений массы стали марки 35Л. В процессе обработки данных мы убедились, что брака в данном производстве нет, так как массы отливки находится в пределах доверительного интервала, что удовлетворяет производству и позволяет производить отливки из стали марки 35Л с высокой точностью.  |
