эконометрика. ммм вар 7. 1. Ситуационная (практическая) часть Предоставить подробное решение задачи 2 и задачи 3 с необходимыми чертежами. Задача 2
 Скачать 0.5 Mb.
|
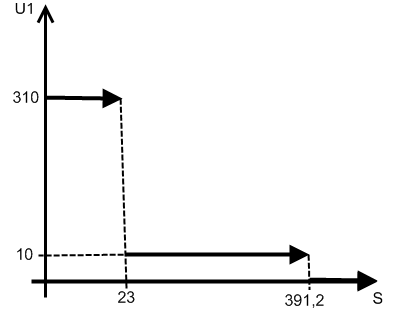
Содержание 1. Ситуационная (практическая) часть………………………………………………..3 2. Тестовая часть………………………………………………………………………14 Список литературы……………………………………………………………………16 1. Ситуационная (практическая) часть Предоставить подробное решение задачи 2 и задачи 3 с необходимыми чертежами. Задача 2 Применяя данные таблицы задачи 1, построить график функции предельной полезности сырья для данного предприятия. В задаче оптимизации выпуска продукции оптимальное решение достигается в точке В(45; 14), являющейся точкой пересечения прямых (1) и (2). Найдем интервал устойчивости изменения сырья.(см. рис.2.1) 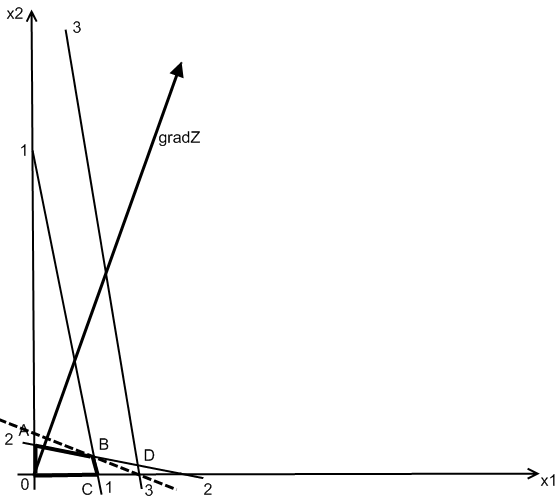 Рис. 2.1 Количество используемого сырья, соответствующего точке D (76,7 ; 7,7) (D – точка пересечения прямых (2) и (3)):  кгКоличество используемого сырья, соответствующего точке А (0 ; 23):  При изменении объема используемого сырья от 23 до 391,2 кг точка B оптимального решения будет перемещаться в пределах отрезка AD и будет соответствовать точке пересечения линий (1) и (2). Координаты этой точки можно найти из системы уравнений: 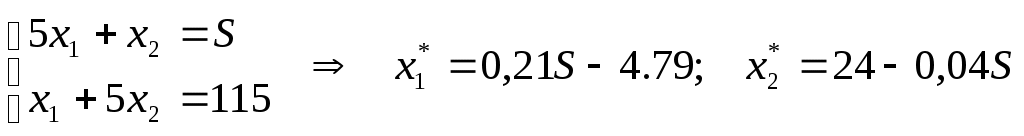 Используя условие дополняющей нежесткости, имеем: 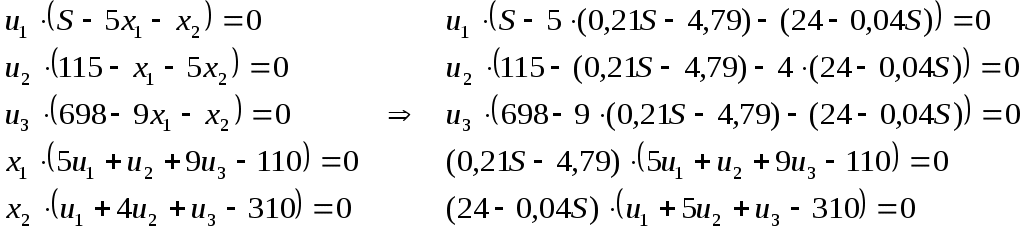 Таким образом, получаем (имея в виду, что 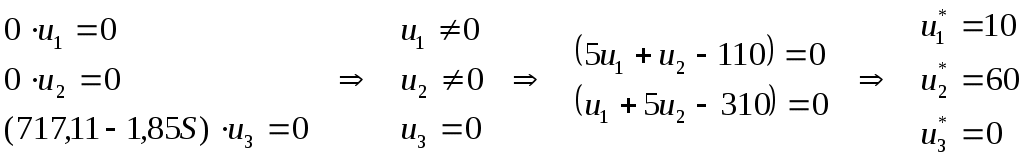 ): Тогда  Очевидно, что дальнейшее увеличение сырья не окажет никакого влияния на изменение оптимального решения, т.е. при  .Пусть S<23, тогда координаты точки В, соответствующей оптимальному решению находятся из уравнения  при условии х1 =0. Следовательно,  .При уменьшении S от 23 до 0 оптимальная точка В будет перемещаться вдоль отрезка АО, тогда оптимальное решение будет иметь вид:  Согласно условию дополняющей нежесткости имеем: 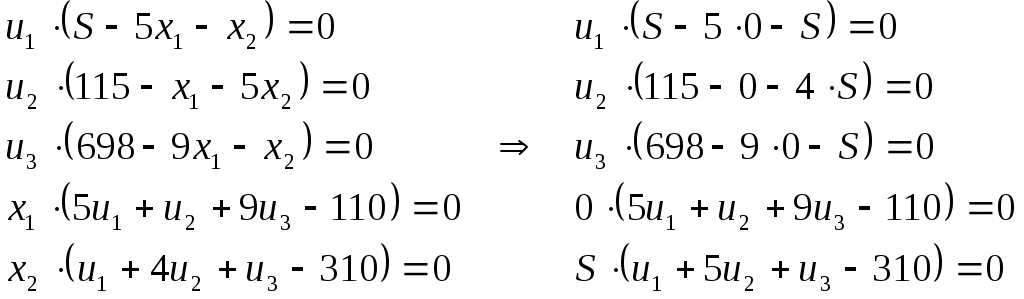 Так как  Так как  Так как  Имеем систему уравнений: 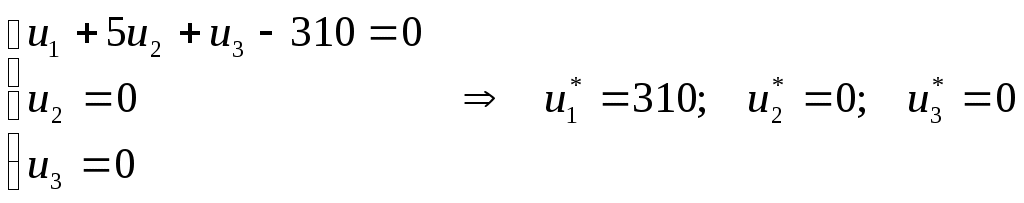 Следовательно,  .В итоге для всех возможных значений 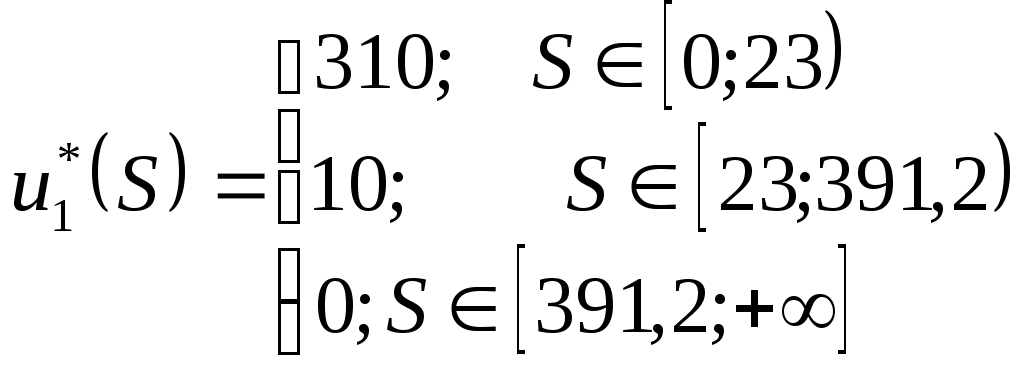 функция предельной полезности: График функции предельной полезности сырья изображен на рисунке 2.2. |
