1.Случайные события. Виды случайных событий.
Событие – это то, что наступает или не наступает в результате эксперимента.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно точно не произойдет в условиях данного опыта.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться.
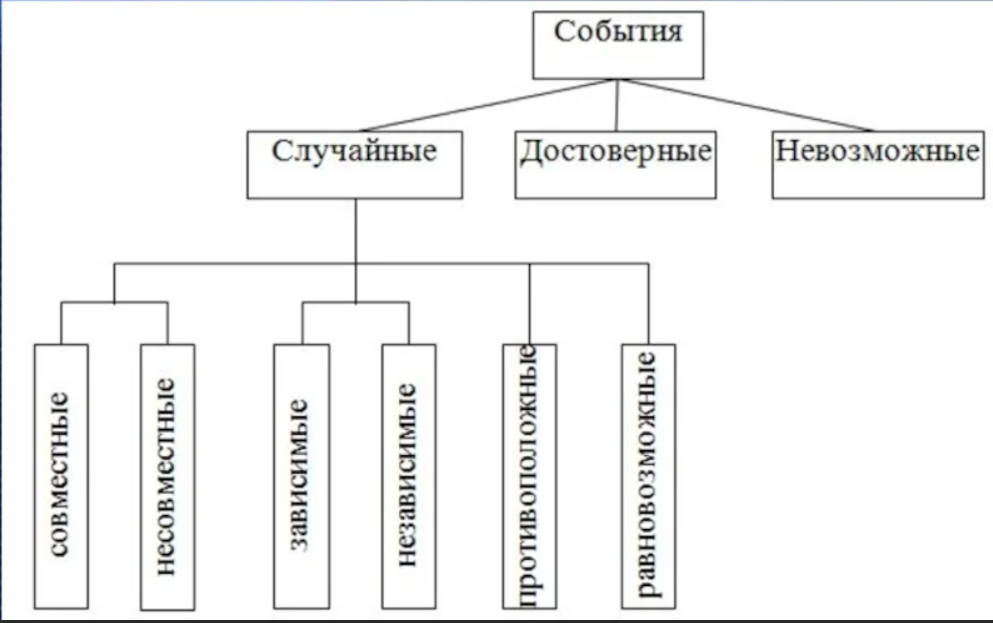
Несовместными называются события, которые в одном опыте не могут произойти одновременно. Два события называются совместными, если появление одного не исключает появления другого.
Два события называются Противоположным, если при наступлении одного, второе произойти не может. Два события наз-ся равновозможными, если нельзя считать, что одно из них более возможно, чем другое.
2. Операции над случайными событиями. 
3. Классическое определение вероятности.
Если эксперимент имеет n возможных исходов, и m из этих исходов благоприятствуют событию А, то вероятность события А
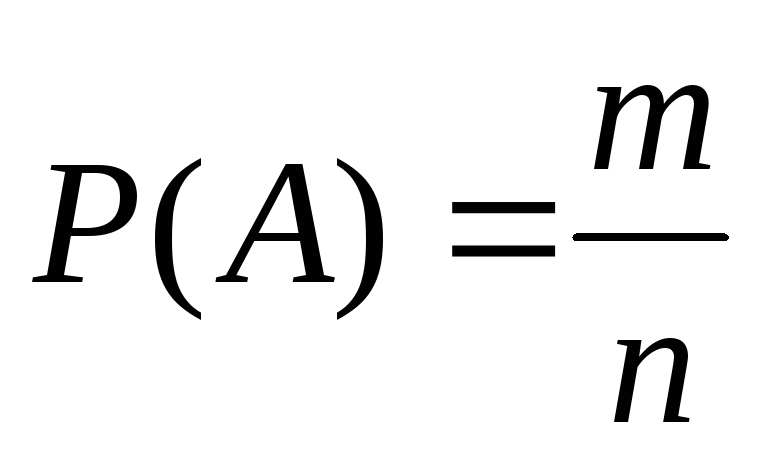 . .
4. Статистическое определение вероятности.
Проводится N опытов (число N должно быть достаточно большим); если в этих опытах событие А появилось M раз, то вероятность события А принимают равной
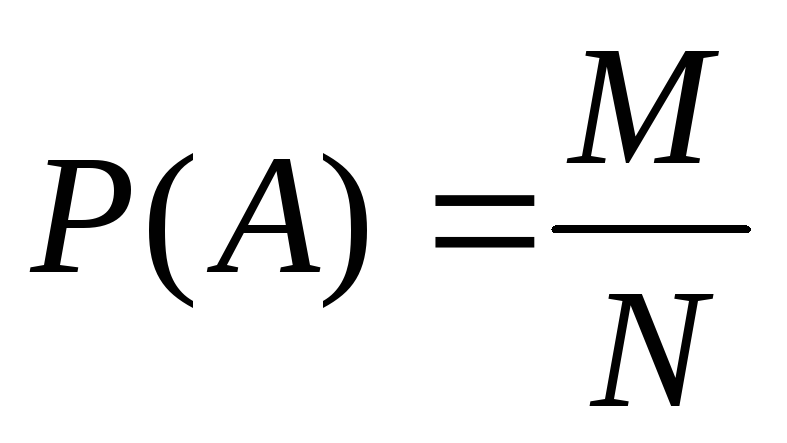
5. Геометрическое определение вероятности.
Пусть исследуются точки некоторого отрезка длины K; событие А заключается в том, что случайная точка попадает в отрезок длины k , содержащийся в исходном отрезке; в этом случае вероятность события А
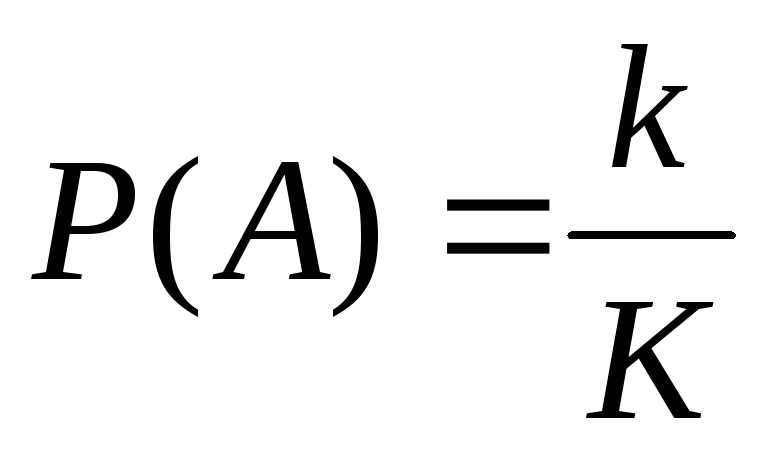 . .
6. Теоремы сложения вероятностей.
Р(А+В) = Р(А)+Р(В)–Р(АВ)-совместимы,
если события А и В несовместны, то Р(А+В) = Р(А)+Р(В).
Сумма вероятностей противоположных событий всегда равна единице:
Р(А)+Р( ) = 1. ) = 1.
7. Теоремы умножения вероятностей.

8. Формула полной вероятности. Формула Байеса.
Пусть имеется несколько предположений об условиях проведения опыта: Н1, …, Нn (гипотезы) с известными вероятностями Р(Н1), …, Р(Нn) (Р(Н1) + … + Р(Нn) = 1), и известны условные вероятности некоторого события А: Р(А/Н1), …, Р(А/Нn). Тогда вероятность события А вычисляется по формуле:
Р(А) = Р(Н1)Р(А/Н1)+…+ Р(Нn)Р(А/Нn) (формула полной вероятности).
Если опыт произведен, и событие А появилось, то новые вероятности гипотез вычисляются по формуле:
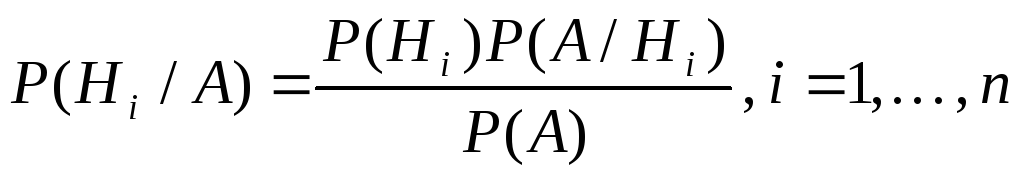 (формула Байеса). (формула Байеса).
9. Независимые испытания. Формула Бернулли.
Пусть проводится n независимых испытаний, в каждом из которых может появиться случайное событие А; вероятность появления события для каждого испытания равна p. Данную серию испытаний называют схемой Бернулли. Вероятность того, что в этой серии испытаний событие А произойдет ровно m раз, равна
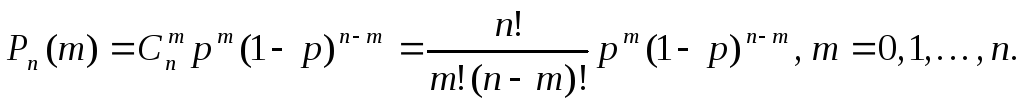
Вероятность того, что событие А появится хотя бы m раз (не менее m раз):
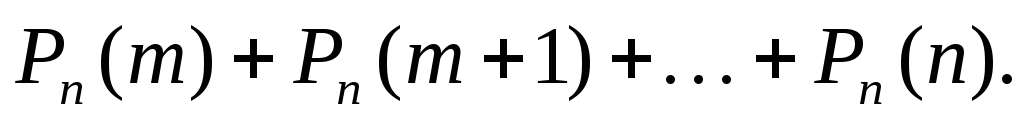
Вероятность того, что событие А появится не более m раз:
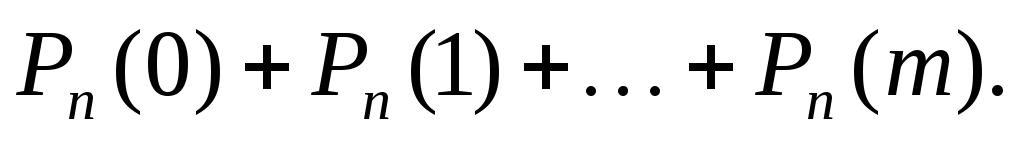
10. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.

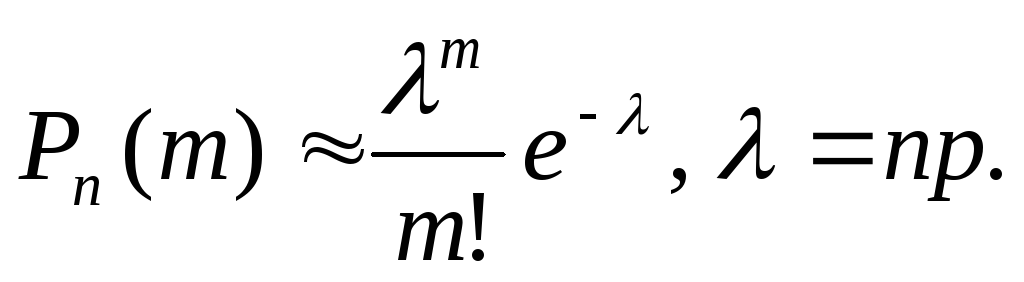
Теорема (локальная теорема Лапласа). Если вероятность появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность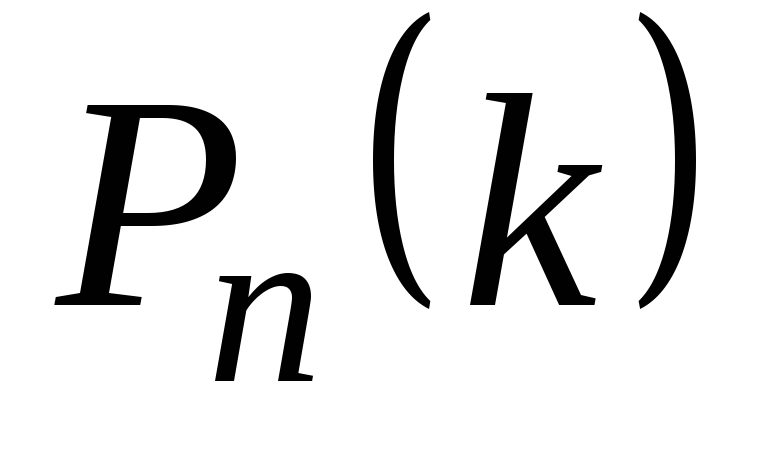 того, что событие А появится вnнезависимых испытаниях ровноkраз, приближенно равна значению функции: того, что событие А появится вnнезависимых испытаниях ровноkраз, приближенно равна значению функции:
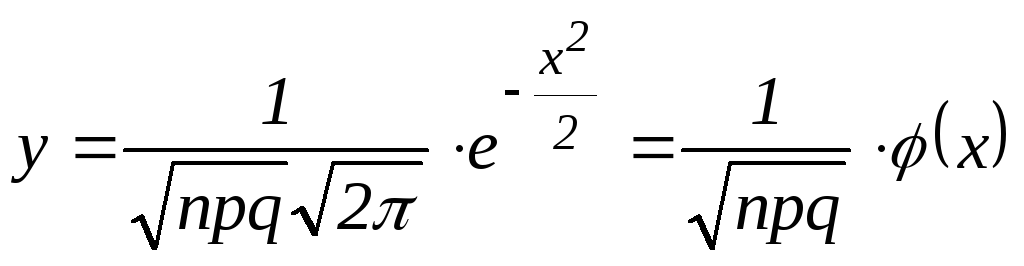 , ,
где
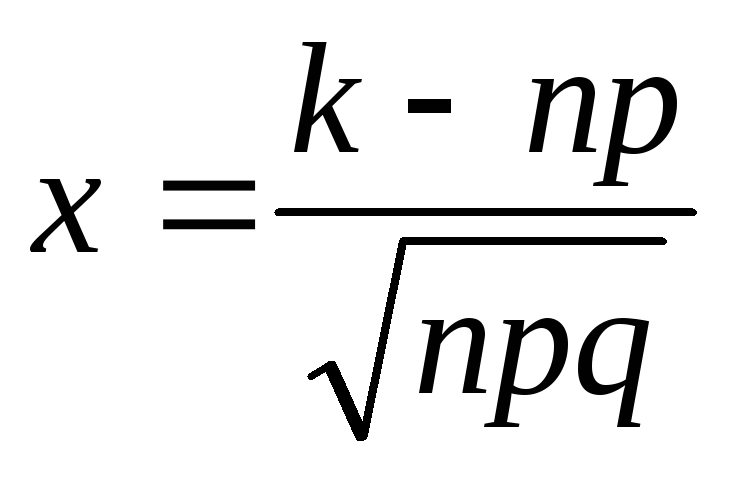 .. ..
Интегральная теорема Лапласа.
Вероятность того, что в nнезависимых испытаниях событие А появится не менее k1 раз и не более k2 раз вычисляется по интегральной теореме Лапласа.
Теорема (интегральная теорема Лапласа). Если вероятность р наступления события а в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А вnиспытаниях появится не менееk1раз и не болееk2раз приближенно равна значению определенного интеграла:
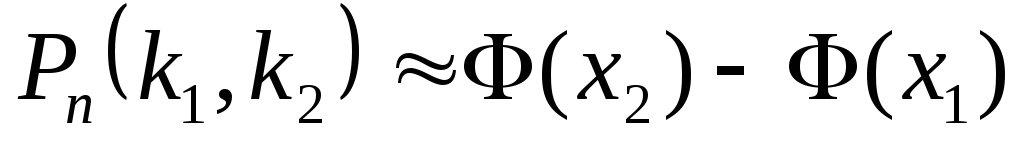 , ,
где
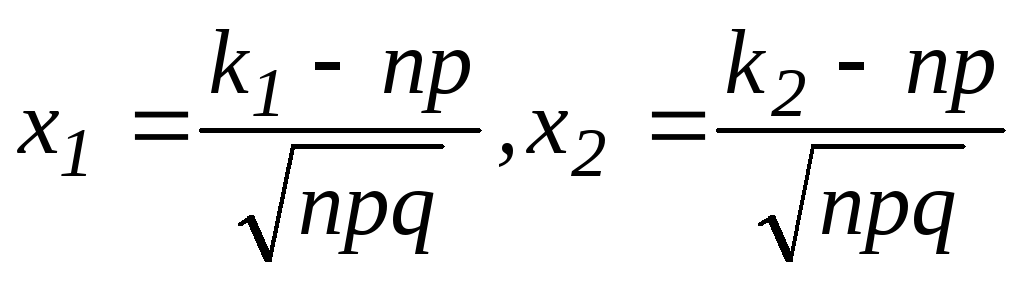 . .
11. Случайная величина. Закон распределения случайной величины.
Случайной называют величину, которая принимает свое значение в зависимости от результата опыта.
Дискретные случайные величины принимают отдельные (изолированные) значения, непрерывные случайные величины – все значения некоторого числового интервала.

12. Функция распределения случайной величины, ее свойства.

13. Плотность распределения случайной величины, ее свойства.
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.
Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:
P{x£X
Плотность вероятности на этом участке определяется отношением
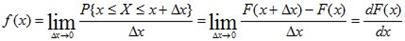
Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.
Основные свойства плотности распределения:
1. Плотность распределения неотрицательна: f(x) ³ 0.
Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.
2. Условие нормировки: 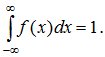 Это свойство следует из формулы, если положить в ней x=∞. Это свойство следует из формулы, если положить в ней x=∞.
Геометрически основные свойства плотности f(x) интерпретируются так:
-вся кривая распределения лежит не ниже оси абсцисс;
-полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
14. Математическое ожидание дискретной и непрерывной случайной величины, его свойства.
Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
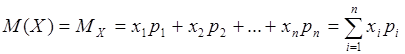 , ,
где 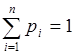
Математическое ожидание 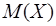 случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины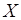 . .
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Это же справедливо и для непрерывных случайных величин.
Свойства математического ожидания.
Математическое ожидание постоянной равно самой постоянной:
М(С) =С. (7.2)
Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение Сс вероятностью р= 1, то М(С) =С·1 =С.
Постоянный множитель можно выносит за знак математического ожидания:
М(СХ) =С М(Х). (7.3)
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
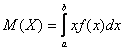
Замечание 1. Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной, а формула для ее вычисления имеет вид:
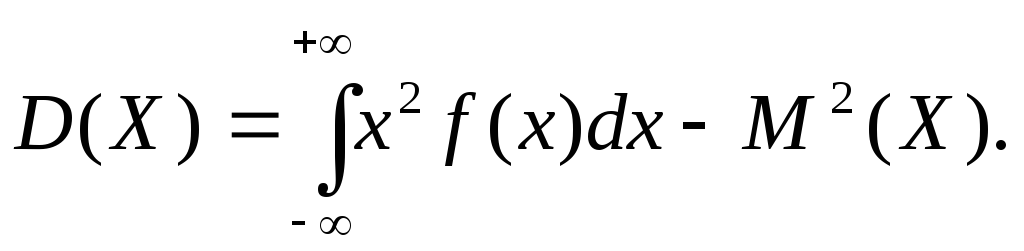
Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a, b], то интегралы в формулах вычисляются в этих пределах.

15. Дисперсия и среднее квадратическое отклонение дискретной и непрерывной
случайной величины, их свойства.
Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2


Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2· D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)
Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

16. Мода, медиана, асимметрия, эксцесс. Моменты случайной величины.

Мода – наиболее часто встречающееся в числовом ряду значение.
Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.

Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии дискретной случайной величины вычисляется по формуле. Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее.
Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада». Коэффициент эксцесса дискретной случайной величины вычисляется по формуле

Эксцесс характеризует "крутизну" подъема кривой распределения по сравнению с нормальной кривой: если эксцесс положителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину.

17. Биномиальный закон распределения дискретной случайной величины.
Дискретная случайная величина Х распределена по биномиальному закону, если она принимает значения 0,1,2…,m…,n… с вероятностями, которые находятся по формуле Бернулли:
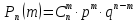
Теорема. Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равняется произведению числа всех испытаний на вероятность наступления события в отдельном испытании, то есть
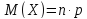 . .
Дисперсия равняется произведению числа всех испытаний на вероятность наступления и не наступления события в отдельном испытании, то есть
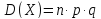 . .
18. Закон распределения Пуассона дискретной случайной величины.
Дискретная случайная величина распределена по закону Пуассона, если она принимает значения 0,1,2…m…n…, бесконечное, но счетное число раз, с вероятностями, определяемыми по формуле Пуассона:
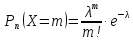
где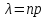 ,p ,p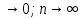 . .
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру Пуассона.
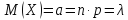
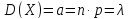
19. Геометрическое распределение дискретной случайной величины.
Дискретная случайная величина распределена геометрически, если она принимает значения 1,2,…m …(бесконечное, но счетное количество раз) с вероятностями, находящимися по формуле общего члена геометрической прогрессии:
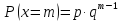
Случайная величина X = m, распределенная геометрически, представляет собой число испытаний (m) до первого положительного исхода.
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной геометрически, вычисляются по формулам:
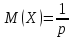
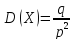
20. Равномерное распределение непрерывной случайной величины.
Равномерным распределением непрерывной случайной величины называется распределение, в котором значения случайной величины с двух сторон ограничены и в границах интервала имеют одинаковую вероятность. Это означает, что в в данном интервале плотность вероятности постоянна.
Таким образом, при равномерном распределении плотность вероятности имеет вид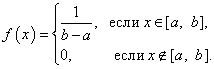
Значения f(x) в крайних точках a и b участка (a, b) не указываются, так как вероятность попадания в любую из этих точек для непрерывной случайной величины равна нулю.
Кривая равномерного распределения имеет вид прямоугольника, опирающегося на участок (a, b) (рисунок ниже), в связи с чем равномерное распределение иногда называют "прямоугольным".
Характеристики равномерного распределения:
среднее значение (математическое ожидание) 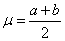 ; ;
дисперсия 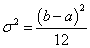 ;стандартное отклонение ;стандартное отклонение 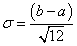 ; ;
равномерное распределение не имеет моды.
21. Показательное распределение непрерывной случайной величины.
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины 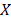 , которое описывается плотностью: , которое описывается плотностью:
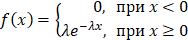
где 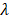 – постоянная положительная величина. – постоянная положительная величина.
Показательное распределение определяется одним параметром 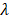 . Эта особенность распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Функция распределения показательного закона: . Эта особенность распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Функция распределения показательного закона:
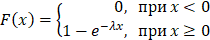
Вероятность попадания в интервал 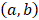 непрерывной случайной величины непрерывной случайной величины 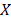 , распределенной по показательному закону: , распределенной по показательному закону:
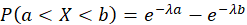
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
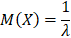
Дисперсия случайной величины, распределенной по показательному закону:
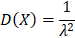
Среднее квадратическое отклонение случайной величины, распределенной по показательному закону:
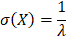
Таким образом, математическое ожидание и среднее квадратическое отклонение экспоненциального распределения равны между собой.
22. Нормальный закон распределения.
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
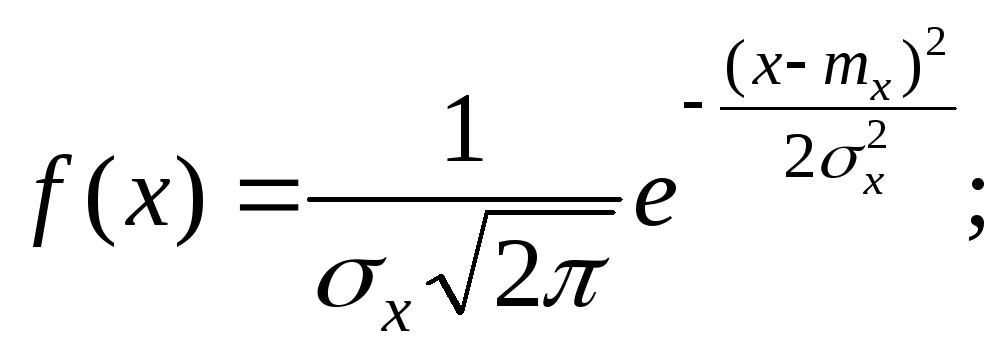
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
23. Генеральная и выборочная совокупности. Закон распределения выборочной
совокупности.
Рассмотрим n объектов, каждый из которых имеет свое значение измеряемого параметра. Общее количество объектов составляет генеральную совокупность. В некоторых случаях неудобно или невозможно получить результаты измерений на всех объектах и поэтому отбирают для проверки определенную часть из этой генеральной совокупности – выборку или выборочную совокупность. Объемом совокупности (выборочной или генеральной) называют число ее объектов. Повторной называют выборку, при которой объект перед отбором следующего возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект не возвращается в генеральную совокупность. В некоторых случаях результаты выборки зависят не только от ее объема, но и от способа отбора объектов. Иногда такой отбор отражает, а иногда не отражает соотношения в генеральной совокупности. Если выборка правильно отражает соотношения в генеральной совокупности, то ее называют репрезентативной (представительной).Общий объем выборки можно определить как 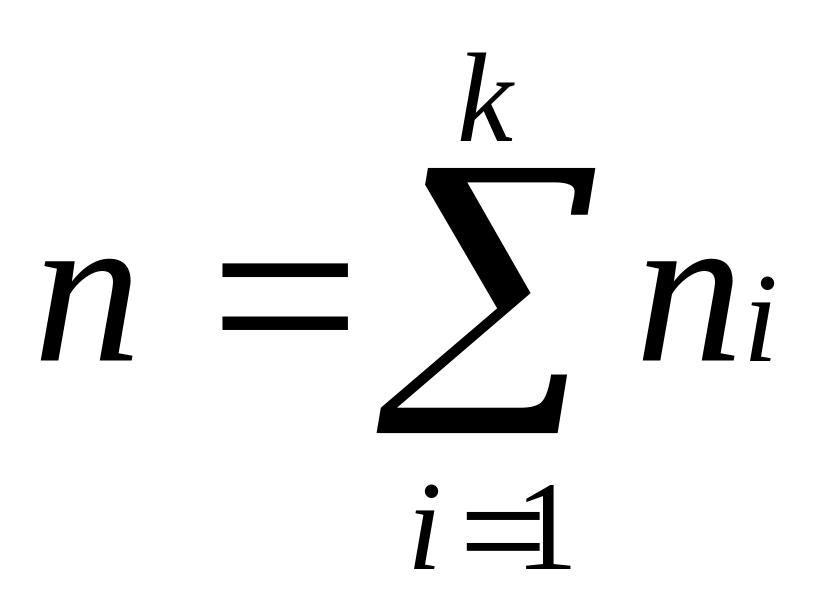
Для установления законов выборочных совокупностей необходимо:
сопоставить вид плотности эмпирического и теоретического распределения;
сравнить коэффициенты асимметрии, эксцессы и коэффициенты вариации статистического и теоретического распределений;
сформулировать нулевую гипотезу;
найти критическую точку;
вычислить наблюдаемое значение критерия Пирсона;
определить закон распределения выборочной совокупности.
Сравнительный анализ относительных частот исследуемых выборочных совокупностей с плотностями нормального, равномерного и показательного распределений позволяет выдвинуть нулевые гипотезы Н0:
выборочная совокупность 1 имеет нормальное распределение с параметрами а=15,87 и σ=4,71;
выборочная совокупность 2 имеет равномерное распределение с параметрами а = 7,16 и b = 32,30;
выборочная совокупность 3 имеет показательное распределение с параметром λ = 0,11.
24. Эмпирическая функция распределения.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию 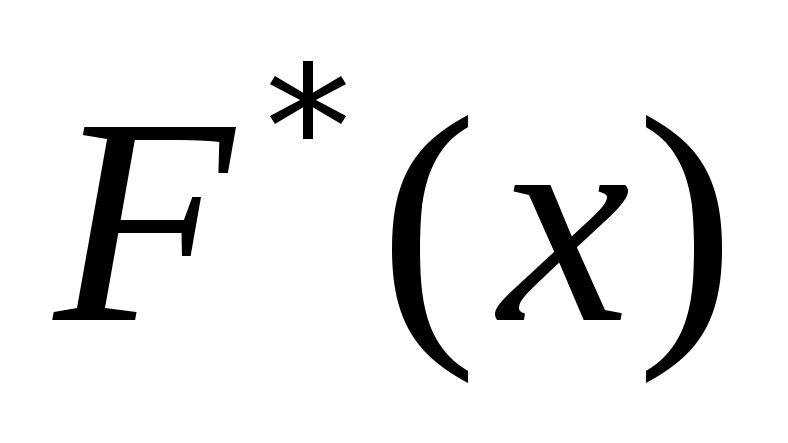 , определяющую для каждого значенияx относительную частоту события , определяющую для каждого значенияx относительную частоту события 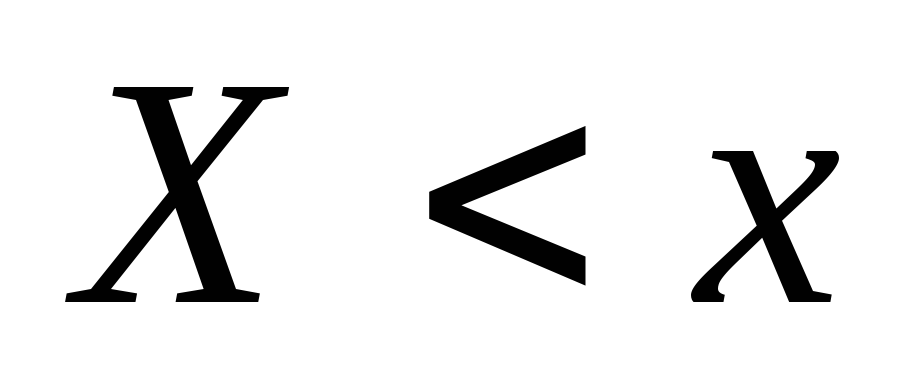 . .
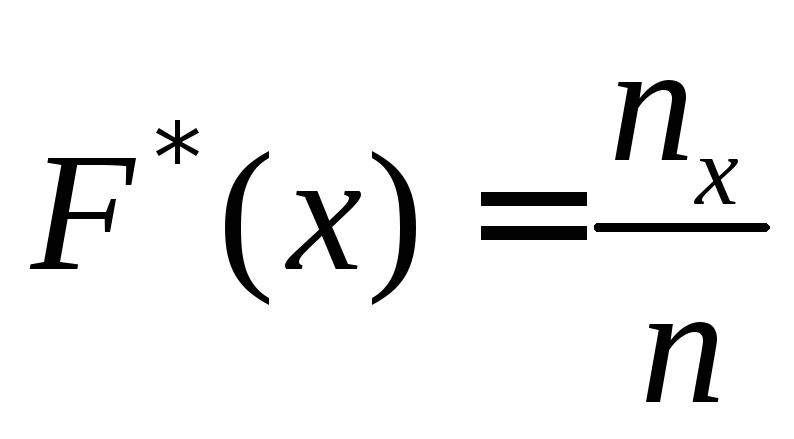

теоретическая функция F(x).
25. Графическое изображение распределения.
Графическое изображение рядов распределения дает наглядное представление о закономерностях распределения.
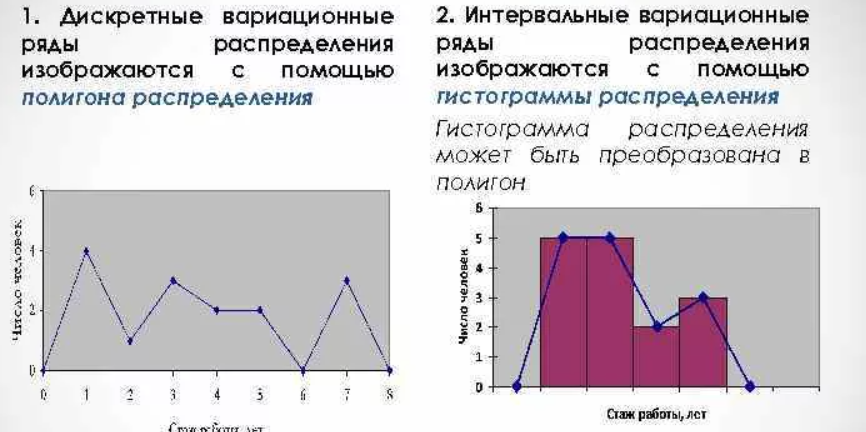
Дискретный ряд изображается на графике в виде ломаной линии – полигона распределения.
Интервальные ряды изображаются в виде гистограмм распределения (то есть столбиков диаграмм) при этом основанием каждого прямоугольника служит величина соответствующего интервала, а высотой его частотная характеристика.
Любая гистограмма может быть преобразована в полигон распределений, для этого необходимо соединить между собой отрезками прямой вершины ее прямоугольников.
При графическом изображении рядов с неравными интервалами по оси ординат
откладываются абсолютные или относительные плотности.
Для характеристики рядов распределения применяют так же графики накопленных частот или куммуляты. Накопленная частота – это сумма частот данного и всех предшествующих интервалов.
Куммулята позволяет определить, какая часть совокупности обладает значе-ниями изучаемого признака не превышающими заданного предела, а какая часть – наоборот – превышает этот предел.
26. Числовые характеристики распределения.
ВСЁ ЧТО БЫЛО ВЫШЕ!

27. Понятие оценки параметров распределения.
Статистической оценкой (в дальнейшем просто оценкой)  параметраθ теоретического распределения называется его приближённое значение, зависящего от данных выбора. параметраθ теоретического распределения называется его приближённое значение, зависящего от данных выбора.
Существует два вида оценок – точечные и интервальные.
Точечной называется оценка, определяемая одним числом. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки.
Интервальной называется оценка, которая определяется двумя числами – концами интервала, в котором с заданной вероятностью заключена оцениваемая величина θ.
28. Точечные оценки параметров распределения.
Точечной оценкой параметра распределения называется число, которое находится по данным выборки. 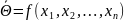 Задача точечной оценки состоит в том, чтобы подобрать функцию, которая на основании выборочных значений дала оценку неизвестного параметра. Точечной распределения оценкой может быть любое число. Задача точечной оценки состоит в том, чтобы подобрать функцию, которая на основании выборочных значений дала оценку неизвестного параметра. Точечной распределения оценкой может быть любое число.
Свойства точечных оценок
Для репрезентативности выборки, выборочные значения должны быть независимыми СВ. Значение независимых СВ, т.е значение точечной оценки будет также случайной величиной.
Точечная оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру. 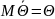
Точечная оценка называется эффективной, если ее дисперсия минимальна, по сравнению с дисперсиями других оценок, полученных на основании выборки того же объема. D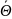 → min → min
Оценка называется состоятельной, если она по вероятности сходится к оцениваемому параметру P( → Θ) →1
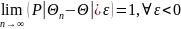
Таким образом формулы точечных оценок параметров распределения нужно выбирать чтобы эта оценка обладала 3-мя свойствами, т.е была не смещенной, эффективной и состоятельной.
29. Интервальные оценки математического ожидания и дисперсии.
Пусть для выборки объема 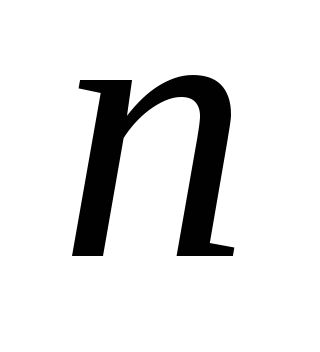 признака признака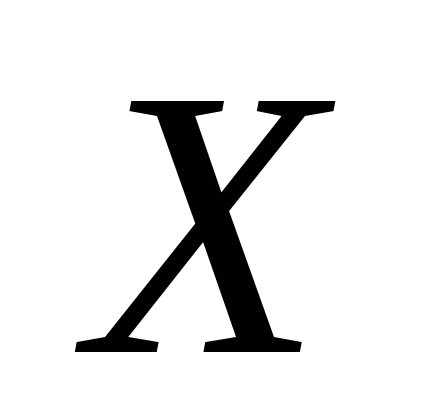 получены среднее арифметическое получены среднее арифметическое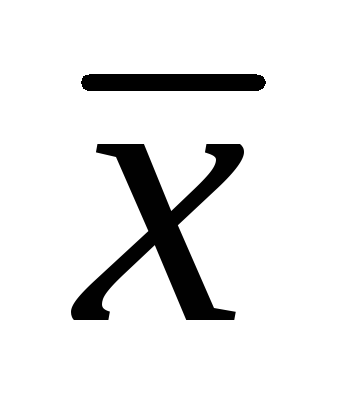 и статистическая дисперсия и статистическая дисперсия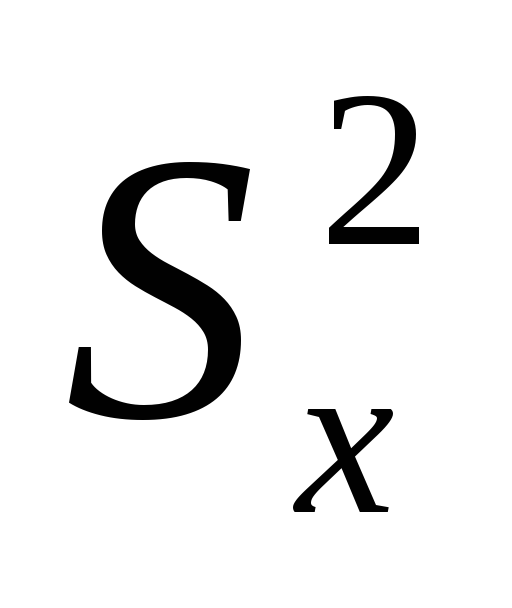 . Зададим промежуток длины . Зададим промежуток длины с серединой в точке с серединой в точке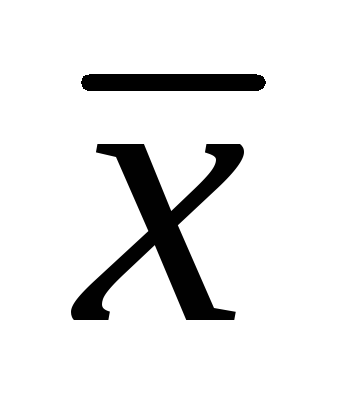 и найдем вероятность и найдем вероятность того, что неизвестное математическое ожидание того, что неизвестное математическое ожидание расположено внутри интервала расположено внутри интервала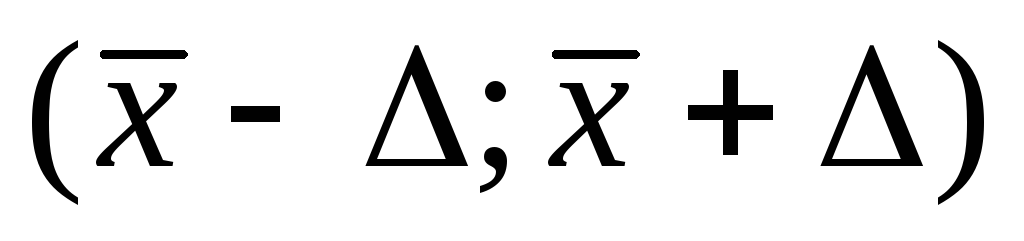 , т.е. найдем , т.е. найдем
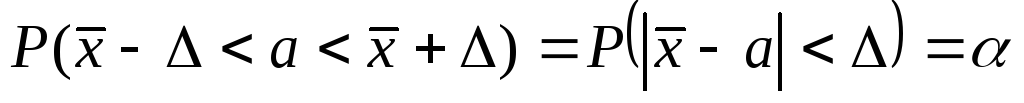 . (9) . (9)
Промежуток  называетсядоверительным интервалом. называетсядоверительным интервалом.
Промежуток  называетсяточностью среднего арифметического. называетсяточностью среднего арифметического.
Величина  называетсядоверительной вероятностью или надежностью среднего арифметического. называетсядоверительной вероятностью или надежностью среднего арифметического.
Здесь возникают три задачи в математической статистике
1)построение доверительного интервала для по заданной надёжности  : :
2) определение  – надёжности оценки математического ожидания – надёжности оценки математического ожидания при заданной точности при заданной точности , ,
3) определение минимального количество опытов 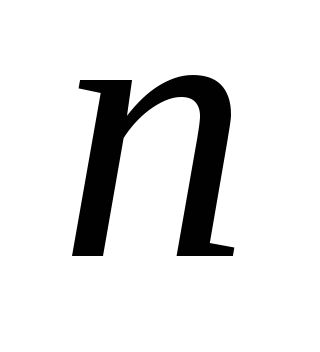 , обеспечивающих необходимые надёжность , обеспечивающих необходимые надёжность и точность и точность при оценке при оценке . .
Построим доверительный интервал для дисперсии D=σ2наблюдаемой случайной величины 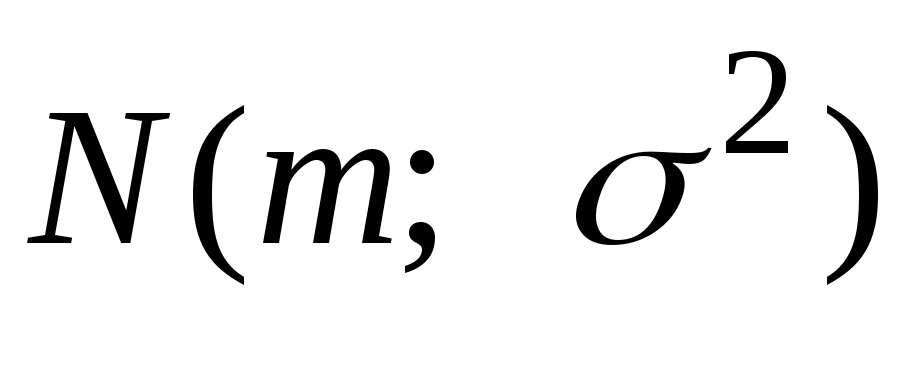 по случайной выборке по случайной выборке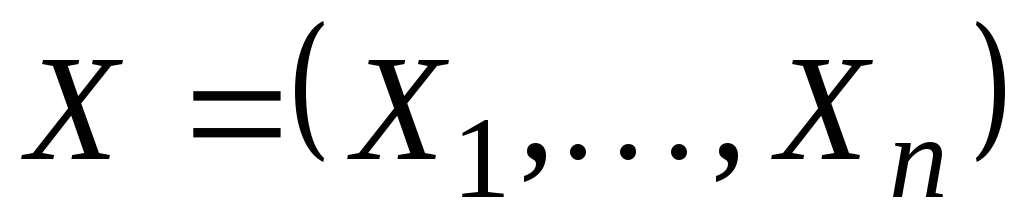 при неизвестном математическом ожидании. при неизвестном математическом ожидании.
Введем случайную величину (статистику) 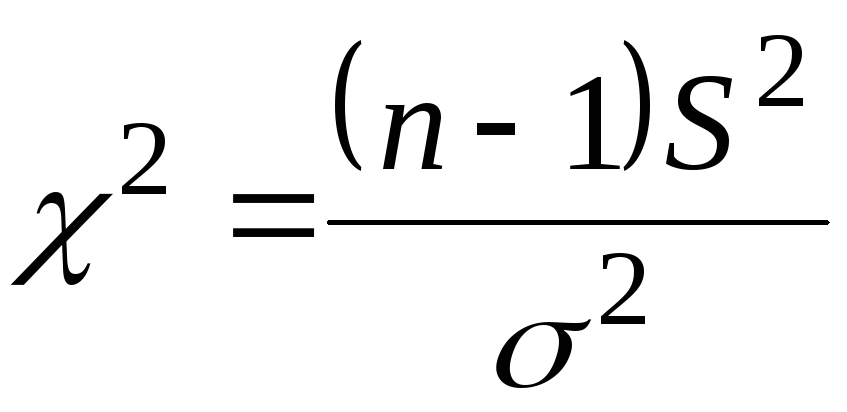 , (3.36) , (3.36)
которая согласно утверждению 2 теоремы Фишера имеет распределение 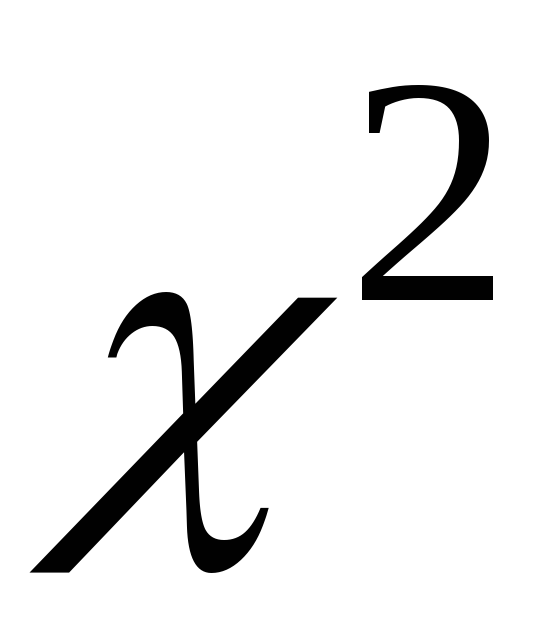 с с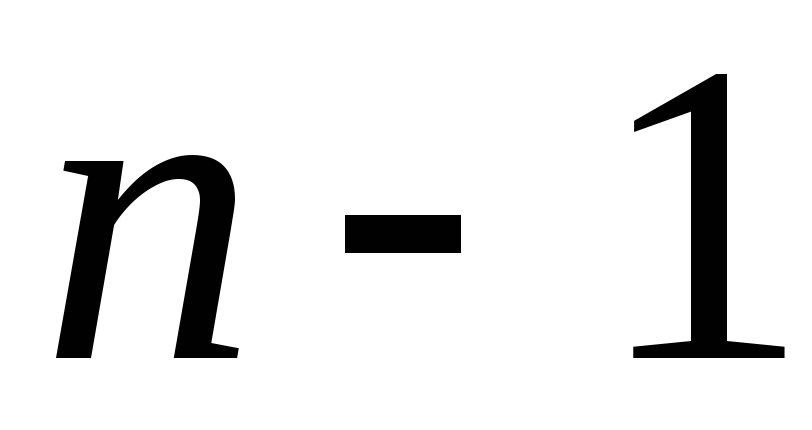 степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде: степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде:
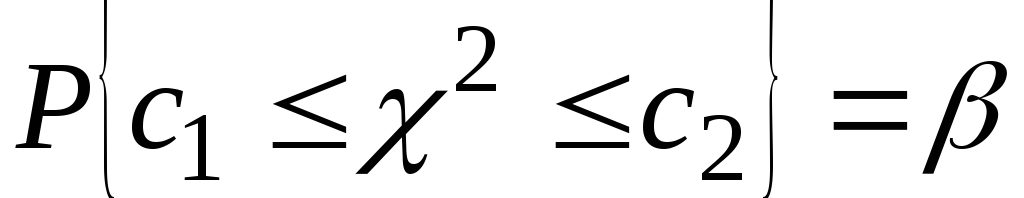 . (3.37) . (3.37)
Обычно доверительный интервал 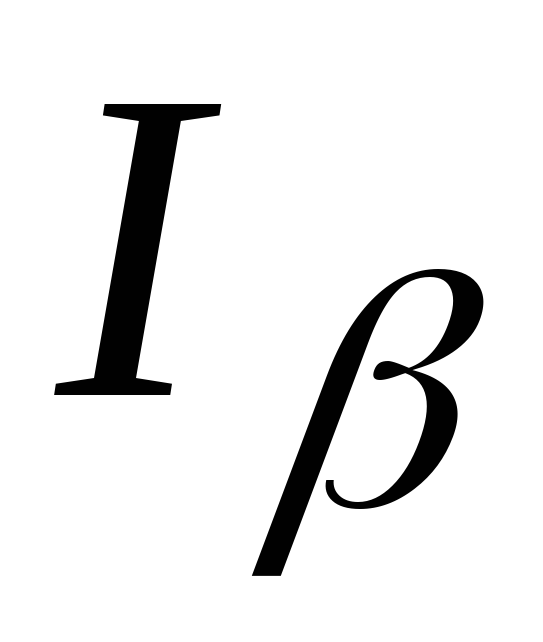 для случайной величины для случайной величины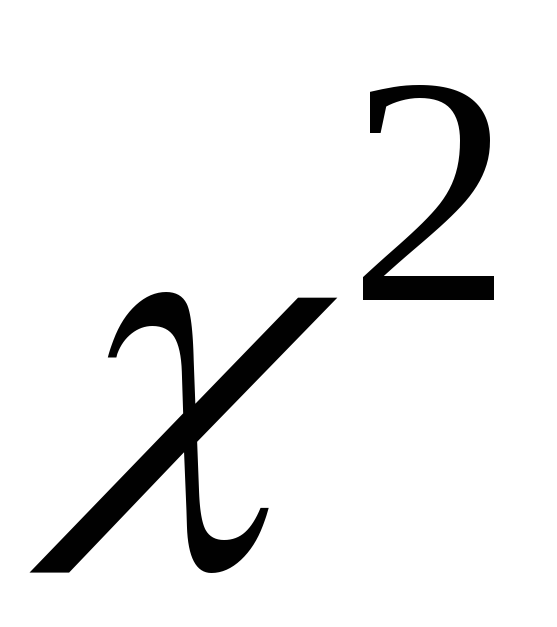 выбирают так, чтобы вероятность ее попадания за пределы этого интервала влево и вправо была одинаковой ( рис. 3.9): выбирают так, чтобы вероятность ее попадания за пределы этого интервала влево и вправо была одинаковой ( рис. 3.9):
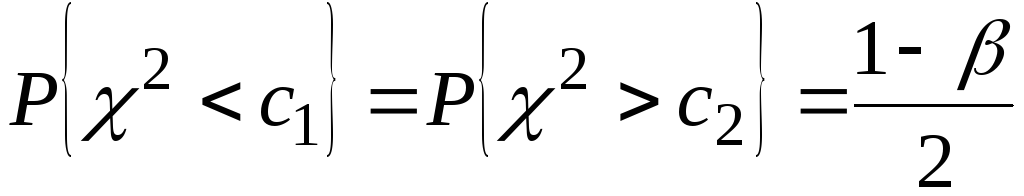 . .
Тогда условия для определения значений 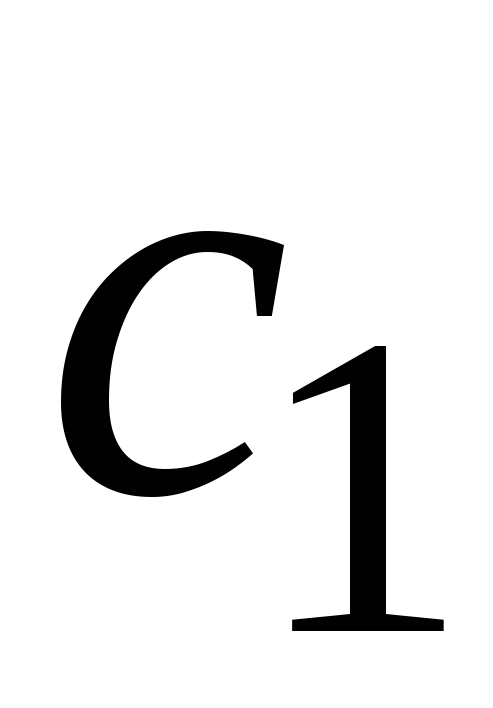 и и  будут иметь вид: будут иметь вид:
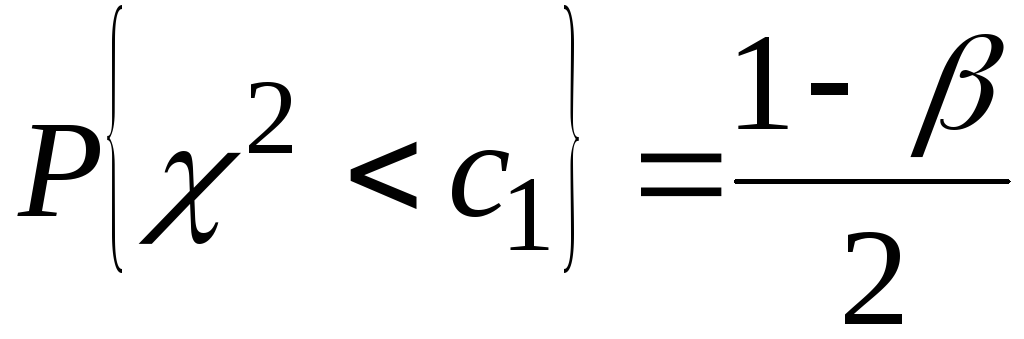 , , 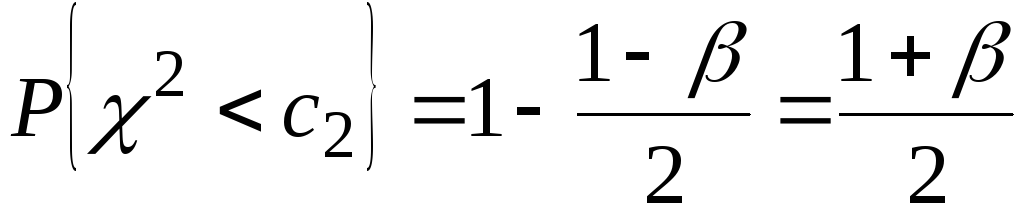 . (3.38) . (3.38)
По таблице квантилей 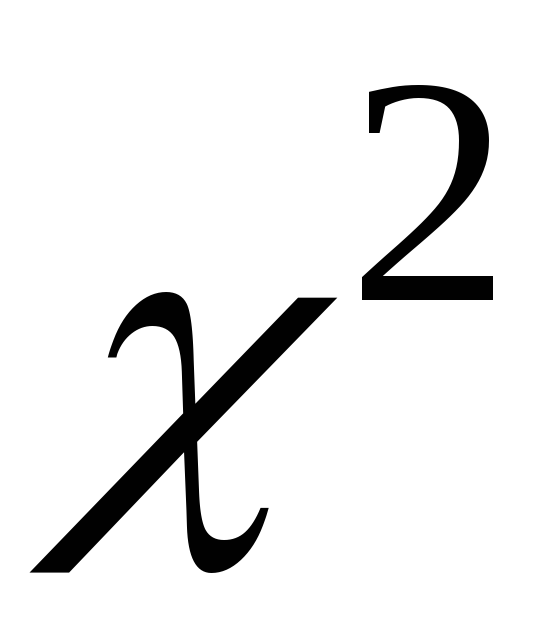 - распределения ( табл. С Приложения) найдем - распределения ( табл. С Приложения) найдем
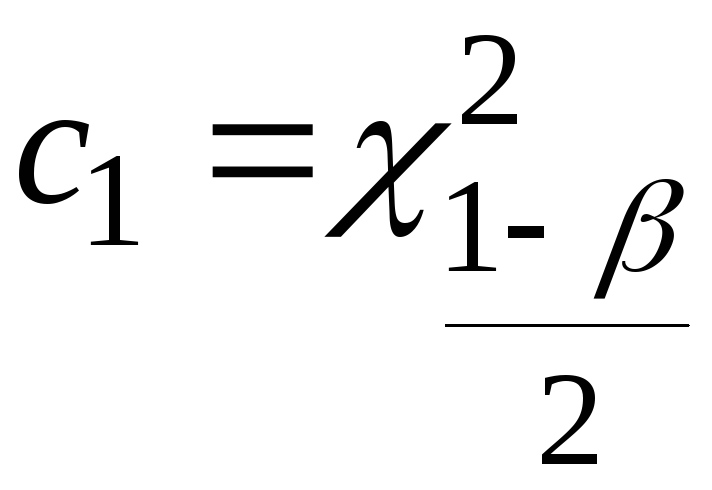 , , 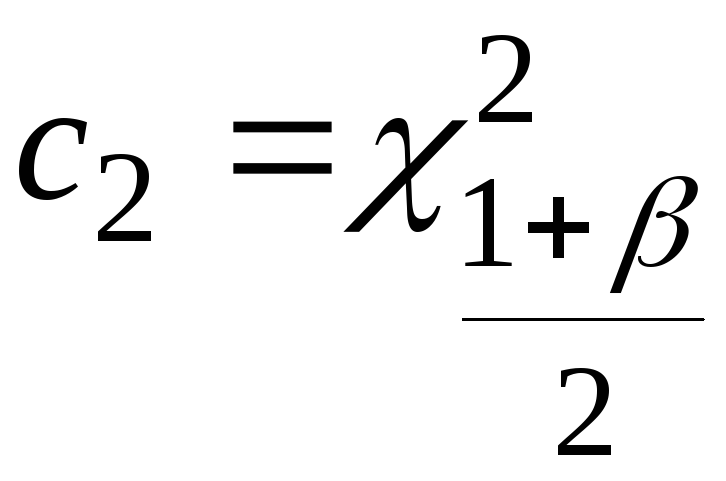 . (3.39) . (3.39)
Неравенства 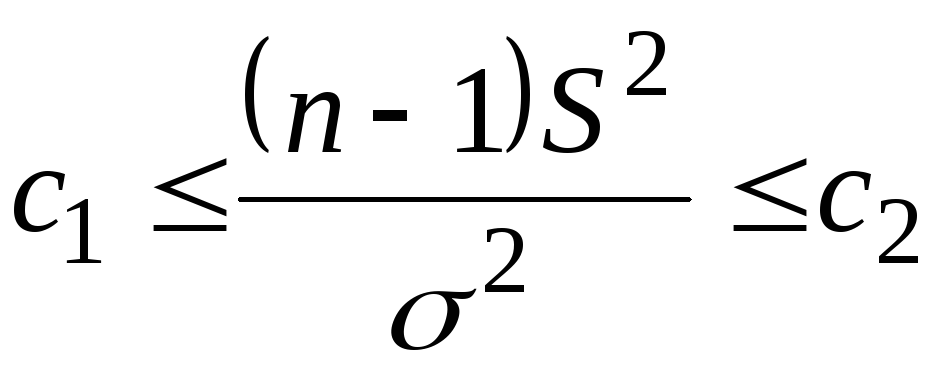 эквивалентны неравенствам эквивалентны неравенствам 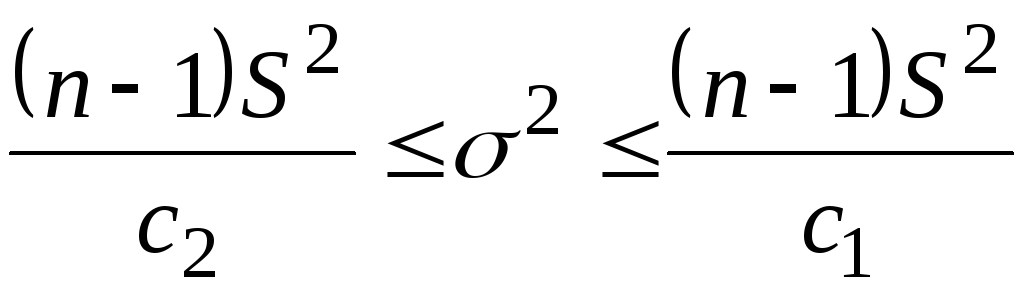 , поэтому , поэтому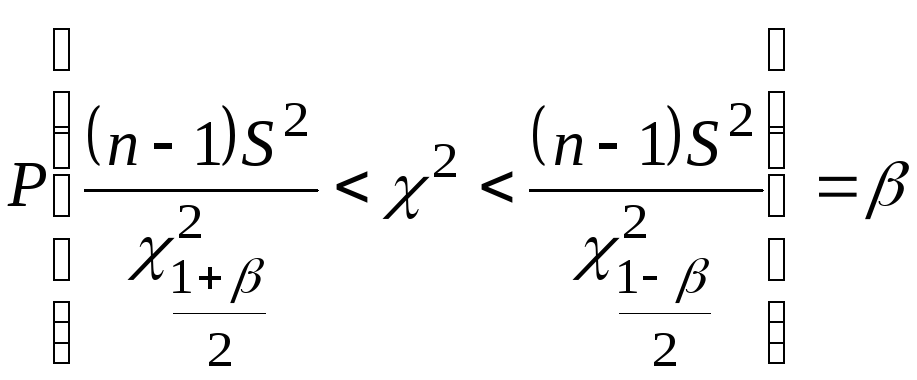 . .
Следовательно, интервал
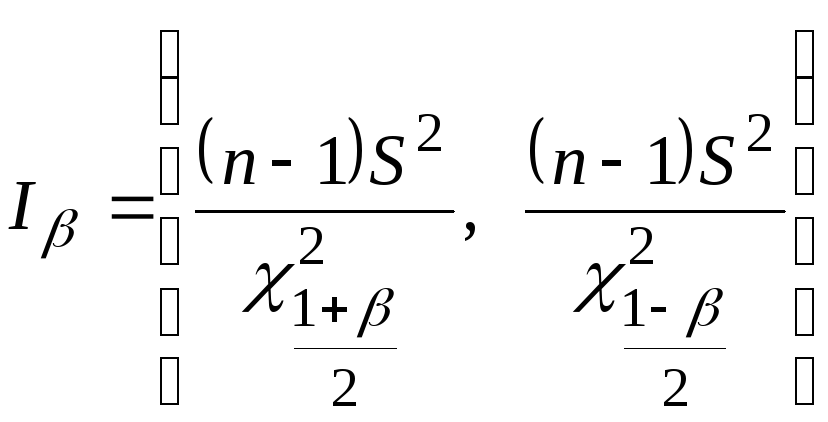 (3.40) (3.40)
является доверительным интервалом дисперсии, соответствующим доверительной вероятности β.
30. Понятие проверки гипотез. Статистическая гипотеза. Статистический критерий.
Проверка гипотез – это наблюдение и формирование предположений на основании полученных ранее данных с целью их подтверждения или опровержения научным методом.
Статистической гипотезой называется гипотеза, которая относится к виду функции распределения, к параметрам функции распределения, к числовым характеристикам случайной величины и т..д, и которую можно проверить на основе опытных данных.
Нулевая гипотеза (H0) – утверждение о параметре генеральной совокупности (параметрах генеральных совокупностей) или распределении, которое необходимо проверить.
Альтернативная гипотеза (HA) – утверждение, противоположное нулевой гипотезе. Выдвигается, но не проверяется. Все гипотезы можно разделить на двусторонние (ненаправленные) и односторонние (направленные). Двусторонние альтернативы (HA : p 6= 0.5) Односторонние альтернативы - левосторонние (HA : p < 0.5) - правосторонние (HA : p > 0.5)
Статистический критерий – правило, которое позволяет делать вывод о том, стоит ли на основе имеющихся данных отвергать нулевую гипотезу или нет. Обычно для критерия определяется соответствующая ему статистика – функция от наблюдений, которая имеет свое распределение. Для того чтобы понять, действительно ли разница между значением параметра в гипотезе и значением оценки, полученной по выборке, является существенной, необходимо сравнить два показателя: наблюдаемое значение статистики и критическое значение статистики
31. Сравнение двух дисперсий нормальных генеральных совокупностей.
При заданном уровне значимости 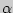 проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:
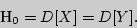
В качестве критерия проверки нулевой гипотезы принимают случайную величину отношения большей исправленной дисперсии к меньшей
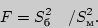
Величина 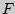 имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы 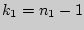 и и 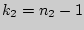 . .
32. Проверка гипотезы о нормальном распределении выборочной совокупности. Критерий
Пирсона.
Чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:
1) по данным выборки объема n найти теоретические частоты 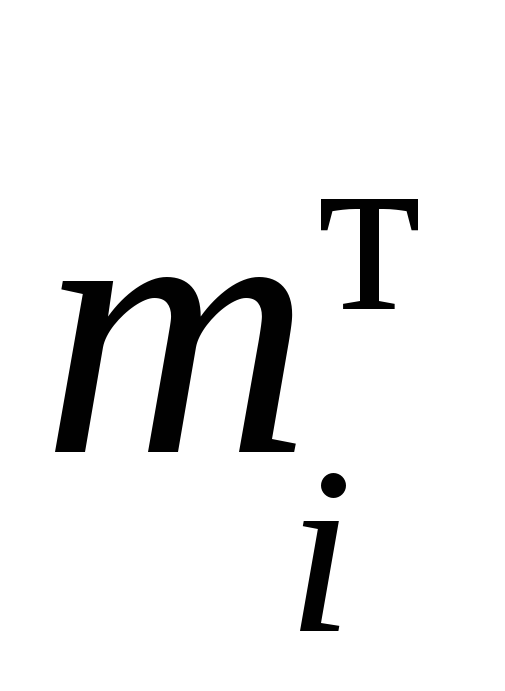 ; ;
2) найти наблюдаемое значение критерия 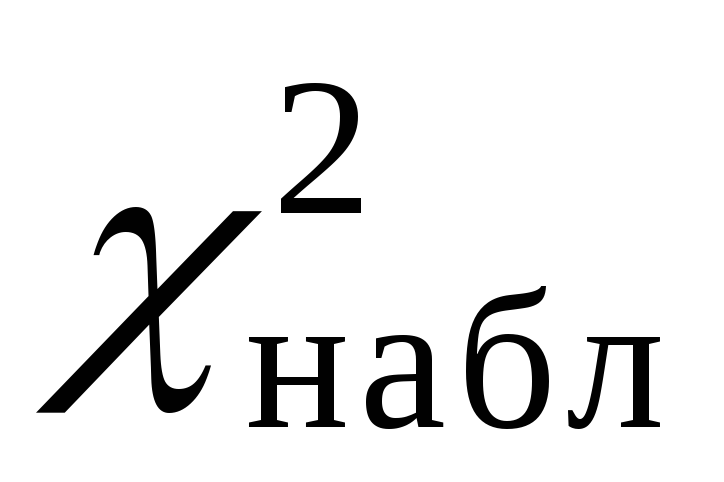 ; ;
3) из таблицы критических точек распределения c 2 (прил. 4 файла «Приложения») по заданному уровню значимости a и числу степеней свободы k=s-3 найти 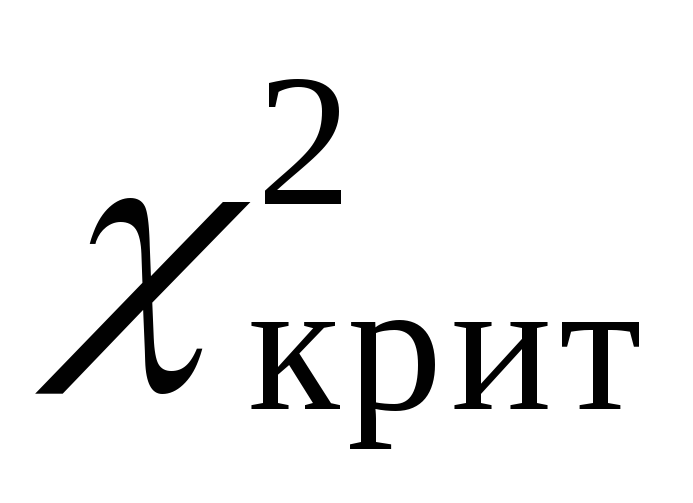 (a, k) - границу правосторонней критической области (a, k) - границу правосторонней критической области
4) сравнить 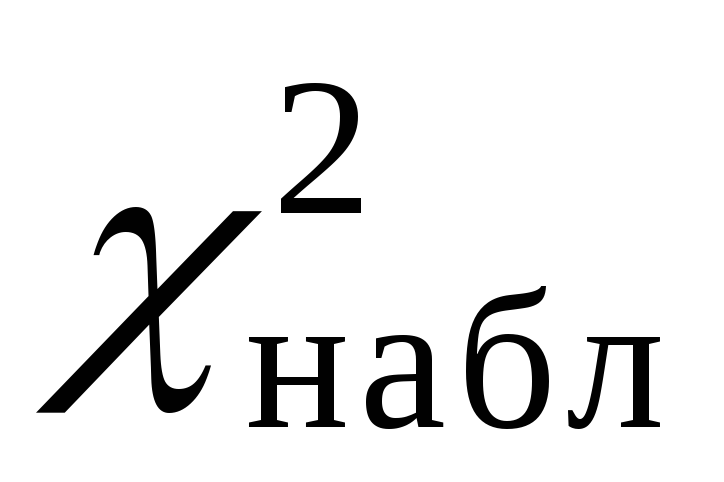 с с 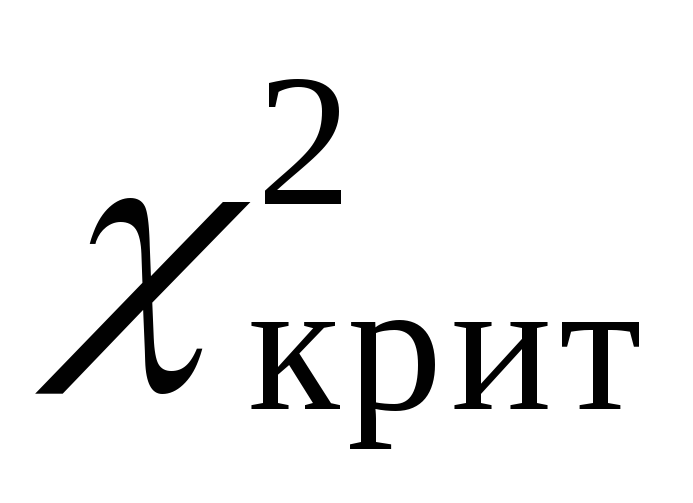 (a, k) и сделать вывод. (a, k) и сделать вывод.
Замечание 1. Необходимые условия применения критерия Пирсона:
1) объем выборки должен быть достаточно велик, по крайней мере не менее 50 наблюдений;
2) каждый частичный интервал должен содержать не менее пяти наблюдений. Если это количество в отдельных интервалах мало, то имеет смысл объединить некоторые интервалы, суммируя частоты.
Замечание 2. Очевидно, что при проверке гипотезы о законе распределения контролируется лишь ошибка первого рода.
 |
 Скачать 5.6 Mb.
Скачать 5.6 Mb.