1. События и операции над ними. Относительные частоты и их свойства
Событием называется произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А.
Все пространство элементарных исходов Ω, если взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
Пустое множество  называется невозможным событием, поскольку оно никогда не происходит. называется невозможным событием, поскольку оно никогда не происходит.
Все остальные события, кроме Ω и  , называются случайными. , называются случайными.
Операции над событиями: 1) Суммой событий А и В называется объединение этих множеств А B. B. 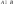 –событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В. –событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.
2) Произведением событий А и В называется пересечение множеств А и В, т.е. А В. Обозначается как АВ. АВ–событие, когда А и В происходят одновременно. 3) Разностью событий А и В называется разность множеств А\В. А\В–событие, которое происходит <=>, когда происходит А и не происходит В. В. Обозначается как АВ. АВ–событие, когда А и В происходят одновременно. 3) Разностью событий А и В называется разность множеств А\В. А\В–событие, которое происходит <=>, когда происходит А и не происходит В.
4) События А и В называются несовместимыми, если  . Если А и В несовместимы, то будем обозначать . Если А и В несовместимы, то будем обозначать  . .
5) Говорят, что событие А влечет событие В, если А является подмножеством В. 6) Событие Ā=Ω\A называется противоположным к событию А.
Пусть А—некоторое событие ( ), N(A)—число тех экспериментов, в которых произошло событие А. Тогда число ), N(A)—число тех экспериментов, в которых произошло событие А. Тогда число 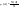 называется относительной частотой события А. Свойства относительных частот: называется относительной частотой события А. Свойства относительных частот:
1) Относительная частота произвольного события А.   . .
2) Относительная частота достоверного события равна 1. 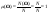
3) (Аддитивность) Относительная частота суммы несовместимых событий 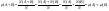
|
2. Аксиомы ТВ. Дискретные пространства элементарных исходов. Классическое определение вероятности.
Аксиомы теории вероятностей.
Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.
Событие—это подмножество Ω, принадлежащее классу F. Любому 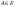 ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы: ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы:
1.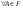 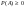
2.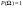 , ,
3.(счетной аддитивности) Если  и и 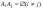 , то , то  . .
Дискретные пространства элементарных исходов.
Бесконечное множество называется счетным, если элементы этого множества можно занумеровать числами натурального ряда (натуральными числами).
Все другие бесконечные множества называются несчетными. Примером несчетного множества может служить [а,b], счетного N.
Пространство элементарных исходов называется дискретным, если оно конечно или счетно.
Вероятностью события А называется число 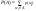 .Сделаем следующие предположения: .Сделаем следующие предположения:
Пространство элементарных исходов  —конечно. —конечно.
Все элементарные исходы равновозможны (равновероятны), т.е.  . .
Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятностью события А называется отношение числа элементарных исходов, благоприятствующих событию А к общему числу элементарных исходов: 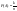 . Это классическое определение вероятности. . Это классическое определение вероятности.
|
3. Элементы комбинаторики. Число выборок
Лемма 1. Из m элементов а1,…,аm первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (аi, bj), содержащих по одному элементу из каждой группы.
Лемма 2. Из n1 элементов первой группы a1, а2,…, аn1,n2 элементов второй группы b1, b2,…,bn2,n3 элементов k-ой группы x1,x2,…,xnk можно составить ровно n1∙ n2∙…∙nk различных упорядоченных комбинаций вида 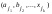 , содержащих по одному элементу из каждой группы. , содержащих по одному элементу из каждой группы.
Все выборки можно классифицировать по 2 признакам: 1) упорядоченные и неупорядоченные, 2) с возвращением и без возращения.
Упорядоченная выборка с возвращением 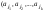 ). Каждый элемент выборки может принимать n значений, т.е. число выборок ). Каждый элемент выборки может принимать n значений, т.е. число выборок 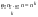 . Упорядоченная выборка без возвращения . Упорядоченная выборка без возвращения  . .
Упорядоченная выборка без возвращения называется размещением. Число размещений 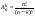 . .
Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке.
Pk-число перестановок из k элементов. 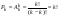 , поскольку 0!=1. , поскольку 0!=1.
Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через.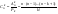 . . 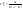 , где , где  . .
|
4. Размещения, перестановки, сочетания. Свойства сочетаний
Упорядоченная выборка без возвращения называется размещением. Число размещений 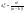 . .
Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке.
Pk - число перестановок из k элементов. 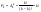 . Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через . Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через 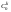 . .
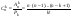 . .  , где , где 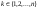 . .
Свойства сочетаний:
1. 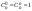 . .
2. 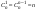 . .
3. 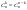 . .
4. 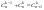 . .
|
5. Геометрические вероятности.
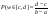 —геометрическая вероятность на прямой. —геометрическая вероятность на прямой.
 —геометрическая вероятность на плоскости. —геометрическая вероятность на плоскости.
 —геометрическая вероятность в пространстве. —геометрическая вероятность в пространстве.
Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности.
|
6. Свойства вероятности
Свойство 1. Вероятность невозможного события равна 0, т.е. P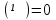 . .
P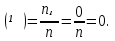
Свойство 2. Вероятность достоверного события равна 1, т.е. P . .
P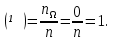
Свойство 3. Для любого события A:0≤P(A)≤1. P(A)= , т. к. 0≤ , т. к. 0≤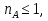 то 0≤ то 0≤ ≤1 и следовательно 0≤P(A)≤1. ≤1 и следовательно 0≤P(A)≤1.
Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
P(A+B)=P(A)+P(B)
P(A+B)=
Свойство 5. (обобщенная теорема сложения вероятностей)
P(A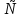 B)=P(A)+P(B)-P(AB). B)=P(A)+P(B)-P(AB).
P(A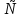 B)= B)=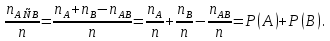
Свойство 6. (теорема сложения k слагаемых)
Если события  попарно несовместимы, то попарно несовместимы, то
P(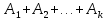 )= P( )= P( )+ P( )+ P(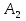 )+…+ P( )+…+ P( ). ).
Свойство 7. Если A B (A влечет B), то P(A)≤P(B). B (A влечет B), то P(A)≤P(B).
B=A+(B\A), тогда P(B)=P(A)+P(B\A)≥P(A).
Свойство 8. Если A B, то P(B\A)=P(B)-P(A). B=A+(B\A). Следовательно, B, то P(B\A)=P(B)-P(A). B=A+(B\A). Следовательно,
P(B)=P(A)+P(B\A). Тогда P(B\A)=P(B)-P(A).
Свойство 9. P(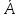 )=1-P(A). )=1-P(A). 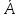 = =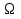 \A, P( \A, P(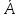 )=P( )=P(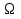 \A)=P( \A)=P(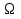 )-P(A)=1-P(A). )-P(A)=1-P(A).
Свойство 10. Если события 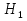 , , 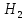 ,…, ,…,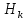 образуют полную группу, то P( образуют полную группу, то P(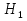 )+P( )+P(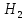 )+…+P( )+…+P(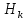 )=1. )=1.
Т.к. 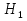 + + 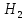 +…+ +…+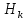 = =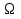 , то по свойству 6: , то по свойству 6:
P(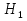 )+P( )+P(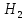 )+…+P( )+…+P(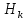 )=P( )=P(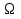 )=1. )=1.
|
7. Условная вероятность. Независимость, независимость в совокупности
Условной вероятностью события B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение 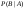 . .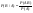 . .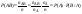 . .
Теорема (умножение вероятностей):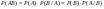 Теорема (обобщенная теорема умножения): Теорема (обобщенная теорема умножения):
События А и В называются независимыми, если 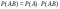 . .
События А и В независимы тогда и только тогда, когда P(B/A)=P(B).
События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если  (для i≠j; i,j (для i≠j; i,j {1,2,3,…,n})–попарная независимость событий; {1,2,3,…,n})–попарная независимость событий;
|
8. Формулы полной вероятности и Байеса
Формула полной вероятности – Если события 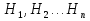 образуют полную группу, то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, равна: образуют полную группу, то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, равна:
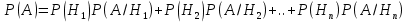

Замечание: При применении формулы полной вероятности, события 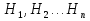 называют гипотезами. называют гипотезами.
Формула Байеса – Пусть события 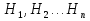 образуют полную группу. A – некоторое событие, которое может произойти совместно с любым из событий, образующих полную группу, причем то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, причем образуют полную группу. A – некоторое событие, которое может произойти совместно с любым из событий, образующих полную группу, причем то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, причем  , тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса: , тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса:
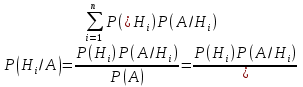
|
9. Испытания Бернулли. Формула Бернулли.
Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей.  , ,  , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
Элементарным исходом будет являться: (w1,w2,…,wn), 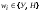 . .
Всего таких исходов 2n.
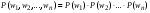 . (1) . (1)
Формула (1) показывает, что события независимы.
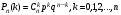 —формула Бернулли. —формула Бернулли.
|
11. Теорема Пуассона
Теорема(Пуассона): Пусть производятся n-независимых испытаний в каждом из которых событие А наступает с вероятностью p, тогда если число испытаний неограниченно возрастает, а вероятность стремится к 0 причем n=p=const , то вероятность того, что событие А появится к раз, в n независимых испытаниях находится по формуле:
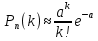 – формула Пуассона – формула Пуассона
Доказательство: По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
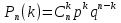 , где q=1-p. , где q=1-p.
Теоремой удобно использовать, когда p->0, a=np≤10.
|
12. Локальная и интегральная теоремы Муавра Лапласа.
Локальная теорема Лапласа
Если вероятность p появления случайного события в каждом испытании постоянна, то вероятность 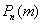 того, что в n испытаниях событие A наступит ровно m раз, приближённо равна: того, что в n испытаниях событие A наступит ровно m раз, приближённо равна:
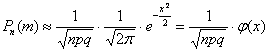 , где , где 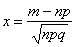
Интегральная теорема Лапласа
Если вероятность p появления случайного события A в каждом испытании постоянна, то вероятность 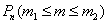 того, что в n испытаниях событие A наступит не менее того, что в n испытаниях событие A наступит не менее 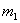 и не более и не более 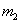 раз (от раз (от 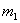 до до 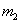 раз включительно), приближённо равна: раз включительно), приближённо равна:
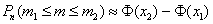
Кроме того, функция Лапласа нечётна: Ф(-х)=-Ф(х), и данное свойство активно эксплуатируется в задачах.
|
13. Случайные величины. Функция распределения и её свойства.
Случайной величиной Х наз. ф-ция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Функцией распределения случайной величины Х наз. функция F(x) действительной переменной х, определяющая вероятность того, что случ. величина Х примет значение, меньшее некоторого фиксированного числа х.
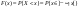 . .
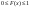 . .
Свойства функции распределения.
1)Функция распределения F(x)–неубывающая функция, т.е. для 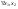 таких что x12 таких что x12 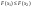 . .
2)Для любых  
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.
3) , , 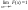 . .
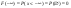 , ,  . .
4)Функция F(x) непрерывна слева. (т.е.  ). ).
5)Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
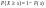 . .
|
14. Дискретные случайные величины. Закон распределения. Биномиальное, геометрическое и распределение Пуассона.
Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е. 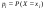 , причем , причем 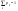 . .
Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения  с вероятностями с вероятностями 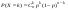
Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 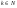 с вероятностями с вероятностями  , где q=1-p. , где q=1-p.
|
Математическое ожидание дискретной случайной величины и его свойства.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 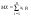 . .
Если случайная величина Х принимает счетное число значений, то 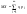 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Свойства математического ожидания:
1) Математическое ожидание постоянной величины равно самой постоянной:
M(C)=C.
2) Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CM(X).
Математическое ожидание случайной величины СХ
|
16. Дисперсия дискретной случайной величины и её свойства.
Дисперсией случайной величины называется число  . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
Дисперсия постоянной величины С равна 0. DC=0.
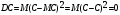 . .
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
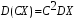 . .
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
|
17. Теоремы о математическом ожидании и дисперсии числа появлений события в независимых испытаниях. Начальные и центральные моменты.
Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события Х в каждом испытании:  . .
Дисперсией случайной величины называется число  . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. Средним квадратическим отклонением случайной величины Х называется число . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. Средним квадратическим отклонением случайной величины Х называется число  . .
Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: . .
Начальным моментом порядка к случайным величинам Х называют мат.ожид. случ. величины Хk:  . В частности, . В частности,  , , 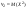 . .
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ)k.
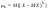 . В частности . В частности 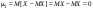 , ,
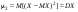 . .
|
18. Непрерывные случайные величины. Свойства плотности распределения.
Говорят, что случайная величина Х имеет плотность вероятности или плотность распределения вероятностей  , если существует функция p(x) такая, что функция распределения , если существует функция p(x) такая, что функция распределения 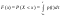
Случайная величина называется непрерывной, если она имеет плотность распределения.
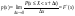 . .
Свойства плотности распределения.
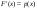 . .
Плотность распределения—неотрицательная функция: 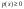 . .
Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:
 . .
Вероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения. 
|
22. Дискретный и непрерывный случайный вектор. Свойства плотности распределения случайного вектора.
Случайный вектор называется дискретным, если все его компоненты-дискретные случайные величины.
Случайный вектор ξ=( называется непрерывным, если существует неотрицательная функция p(x)= называется непрерывным, если существует неотрицательная функция p(x)= , называется плотностью распределения случайных величин , называется плотностью распределения случайных величин 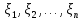 такая что функция распределения такая что функция распределения
Свойства плотности распределения случайного вектора.
Свойство 1. 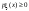
Свойство 2. 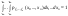 . .
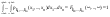
Теорема 1. Пусть ξ=( ) – непрерывный случайный вектор. Тогда случайные величины ) – непрерывный случайный вектор. Тогда случайные величины 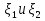 – непрерывны, причем – непрерывны, причем 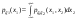 , ,  . .
Теорема 2. Пусть случайная величина Х непрерывна с плотностью 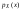 , а случайная величина , а случайная величина  , где , где  — монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность — монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность 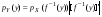 . .
|
23. Числовые характеристики системы двух случайных величин. Ковариация, коэффициент корреляции и его свойства. Асимметрия и эксцесс.
Ковариацией между случайными величинами Х и Y называется число . .
Для непрерывных случайных величин X и Y используют формулу 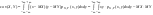
Коэффициентом корреляции между случайными величинами Х и Y называется число  . .
Свойства корреляции.
Абсолютная величина коэффициента корреляции не превосходит единицы, т.е.  . .
Для того чтобы  необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью.
Если случайные величины независимы, то они некоррелированы, т.е. r=0.
Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.
Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0.
Коэффициентом асимметрии случайной величины Х называется число 
Эксцессом случайной величины Х называется число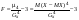 . Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения. . Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.
|
|
| |
 Скачать 195.59 Kb.
Скачать 195.59 Kb.