Метрология Шпоры. 1. Стандартизация, Основные цели, принципы, функции и задачи стандартизации
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
51. Точечные оценки законов распределения. Требования, предъявляемые к ним. Среднее-арифметическое значение измеряемой величины 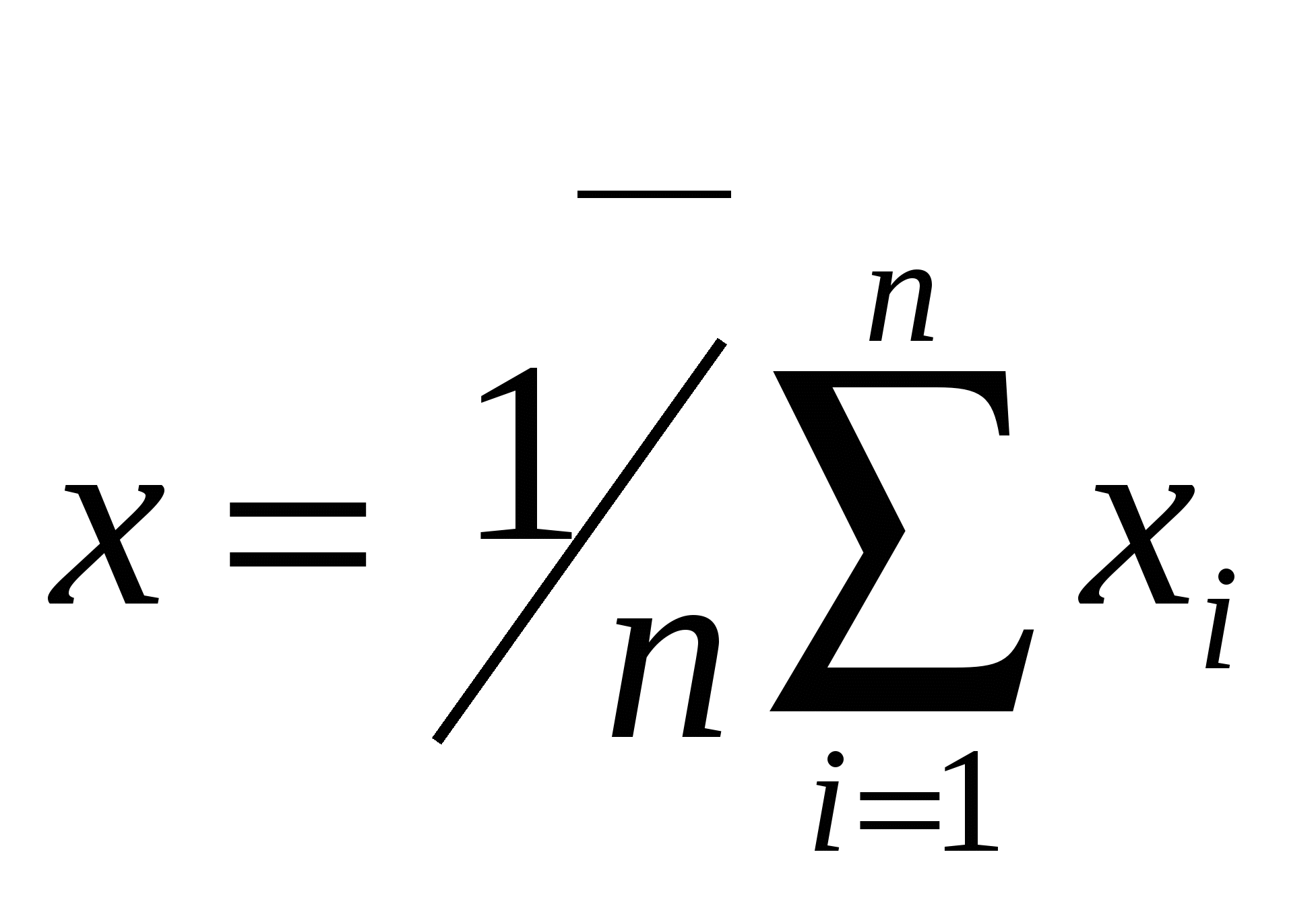 Точечная оценка дисперсии СКО случайной величины х определяется как корень квадратный из дисперсии. Оценка СКО среднего арифметического значения Оценка СКО среднего квадратического отклонения 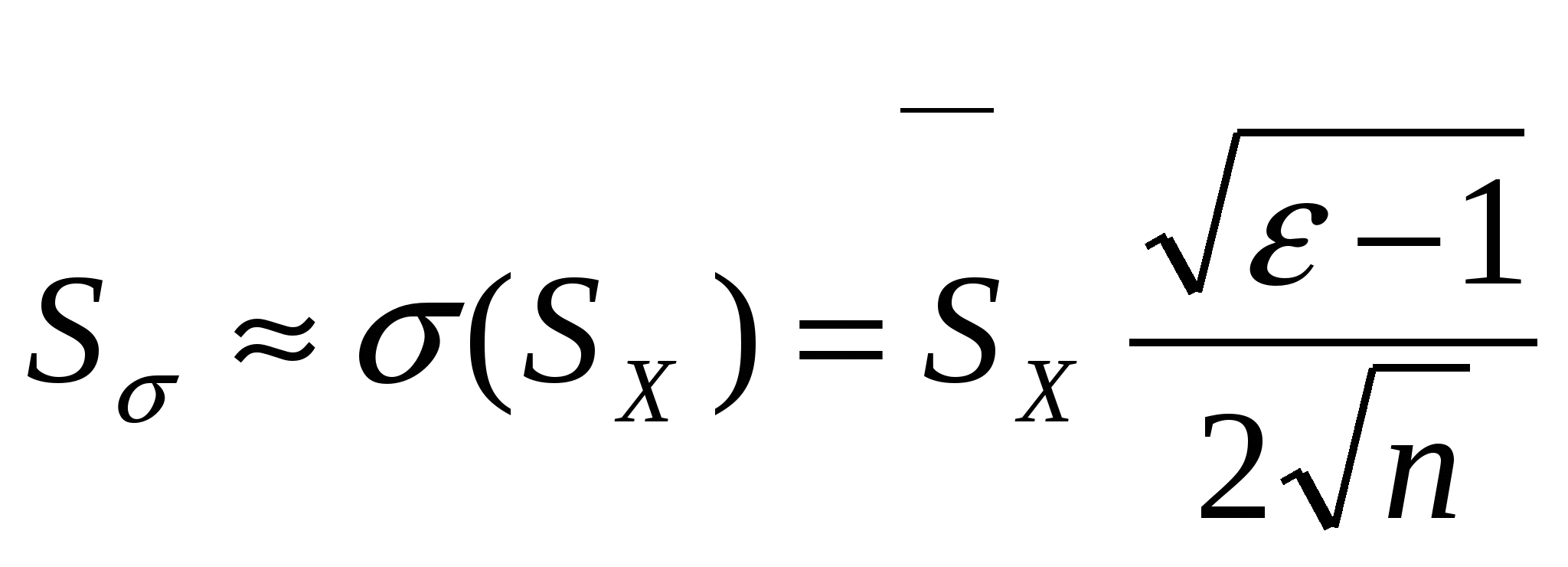 Оценки коэффициента асимметрии и эксцесса находятся по формулам | 53. Прямые многократные измер-ия. Идентиф-ия формы закона распред-ия. Задача обработки рез-ов многократных измер-ий заключ-ся в нахождении оценки измер-ой вел-ны и доверит-ого интервала, в кот-ом нах-ся ее истинное знач-ие. Исходной инфой для обработки явл-ся ряд из n (n>4). рез-ов измерений х1…хn из которых исключены известные систематич-ие погрешности, - выборка. Этапы: 1) определение точечных оценок закона распред-ия рез-ов измеренй (ср. арифм-ое знач. измер-ой вел-ны х, СКО рез-та измер-ия Sx и СКО ср. арифметич. знач-ия Sx). 2) определение закона распред-ия рез-ов измер-ий или случайных погрешностей измер-ий (построение гистограммы, полигона распредел-ия и кумулятивной кривой по которым оценивается закон распред-ия). 3) оценка закона распред-ия по статистич. критериям. При числе наблюдений n<15 принадлежность распред-ия к нормальному не проверяется; при 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52. Доверительный интервал, способы его задания. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, м/у границами кот-го с зад. доверит-ой вер-тью Р наход-ся истинное значение оценив-го параметра. Р{xН | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54. Алгоритм обработки результатов однократн. измер-ий с точным оцениванием. За рез-т прямого однократного измер-ия приним-ся получ-ая вел-на. До измер-ия д.б. проведена априорная оценка составляющих погрешности. При опред-ии доверит. границ погрешности доверит. вер-ть =0,95. Условия применения методики: составляющие погрешностей известны, случ-ые составл-ие рапред-ны по нормальн. закону, а неисключ-ые систематич-ие, заданные своими границами Θi – равномерно. Составляющие погрешности: погрешности ср-в измер-ий, погрешность метода измер-йй, погрешность оператора. Составляющие могут состоять из неисключ-ых систематич. и случайных погреш-ей. При наличии систематич. погрешности доверит. граница рез-та измер-ия: Θ(P)=k√(Σ{1,m} Θi^2) или Θ(P)=k√(Σ{1,m} [(Θi^2(Pj))/kj^2]), где Θi(Pj) – доверит. граница i-ой неисключ-ой систематич. погрешности, kj(=1,1) – коэф-т, зависящий от Pj(=0,95). Случайные составляющие выраж-ся СКО Sxi либо доверит. границами ±εi(P). Доверит. граница случ. составл-ей погрешности: ε(з)=zPSX=zP√[Σ{1,k}Sxi^2], где zP(=2 при Р=0,95) – точка нормир-ой ф-ии Лапласа. ε(з)=zPSX=zP√[Σ{1,k} (ε^2(Pi) /(z_Pi)^2]. Найденные значения Θ и ε(Р) используются для оценки погрешности рез-та прямых однократных измер-ий. В завис-ти от соотнош-ия Θ и Sx суммарная погрешность ΔР опред-ся ф-ми: если Θ/Sx<0.8, то ΔP=ε(Р), если 0.8<Θ/Sx<8 => ΔP=kP[ε(Р)+Θ(P)], где kP – коэф-нт, если Θ/Sx>8 => ΔP=Θ(P). Рез-т запис-ся в виде: x±ΔP при доверит. вер-ти P=P_д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59. Определение единицы и размера физической величины, размерность физической величины. Основные принципы построения систем единиц физической величины. Физическая величина – одно из свойств объекта, явления, процесса, общее в качественном отношении для многих объектов, но в количественном отношении индивидуально для каждого. Единица физической величины – это физическая величина фиксированного размера, которой условно присвоена величина, равная 1, и применяемая для количественного выражения однородных с ней физических величин. Размер физ. величины – количественное содержание в данном объекте св-ва соответствующего понятию физ. величины. Размерность физических величин – это выражение, отражающее связь величины с основными единицами величин системы, в котором коэффициент пропорциональности равен L. | 60. Международная система единиц. Система единиц физических величин – совокупность физических величин, образованная в соответствии с принципами, когда одни величины принимают за независимые, а другие определяются как функции независимых величин. В 1960 г. – на 11 конференции по мерам и весам принята международная система единиц физических величин – система СИ. ГОСТ 8.417-81 – международная система физических величин.
Производные единицы физических величин.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
