Метрология Шпоры. 1. Стандартизация, Основные цели, принципы, функции и задачи стандартизации

• Название: 1. Стандартизация, Основные цели, принципы, функции и задачи стандартизации
• Анкор: Метрология Шпоры.doc
• Дата: 26.04.2017
• Размер: 1.13 Mb.
• Имя файла: Метрология Шпоры.doc
• Тип: Документы; #5771
• страница: 4 из 7

38. Контроль, его отличие от измерения. Виды контроля. Вероятность ошибок 1 и 2 рода, что они характеризуют.
Контроль - - это процесс определения соответствия значения параметра изделия установленным требованиям или нормам.

Сущ­ность всякого контроля состоят в проведении двух основных эта­пов.

На первом из них получают информацию о фактическом со­стоянии некоторого объекта, о признаках и показателях его свойств. Эта информация называется первичной.

На втором — первичная информация сопоставляется с заранее установленными требования­ми, нормами, критериями. При этом выявляется соответствие или несоответствие фактических данных требуемым. Информация о их расхождении называется вторичной.
Измерения и контроль тесно связаны друг с другом, близки по своей информационной сущности и содержат ряд общих операций (например, сравнение, измерительное преобразование). В то же время их процедуры во многом различаются:

• результатом измерения является количественная характерис­тика, а контроля — качественная;

• измерение осуществляется в широком диапазоне значений измеряемой величины, а контроль — обычно в пределах небольшо­го числа возможных состояний;

• контрольные приборы, в отличие от измерительных, применя­ются для проверки состояния изделий, параметры которых заданы и изменяются в узких пределах;

• основной характеристикой качества процедуры измерения явля­ется точность, а процедуры контроля — достоверность.

Контроль может быть классифицирован по ряду признаков.
В зависимости от числа контролируемых параметров он под­разделяется на однопараметровый, при котором состояние объекта определяется по размеру одного параметра, и многопараметровый, при котором состояние объекта определяется размерами многих параметров.
По форме сравниваемых сигналов контроль подразделяется на аналоговый, при котором сравнению подвергаются аналоговые сиг­налы, и цифровой, при котором сравниваются цифровые сигналы.
В зависимости от вида воздействия на объект контроль под­разделяется на пассивный, при котором воздействие на объект не производится, и активный, при котором воздействие на объ­ект осуществляется посредством специального генератора тесто­вых сигналов.
В практике большое распространение получил так называемый допусковыи контроль, суть которого состоит в определении путем измерения или испытания значения контролируемого параметра объекта и сравнение полученного результата с заданными гранич­ными допустимыми значениями.

39. Классификация погрешностей
Истинное значение физической величины — это значение, идеальным образом отражающее свойст­во данного объекта как в количественном, так и в качественном от­ношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить ее в виде числовых значений.
Резуль­тат измерения представляет собой приближенную оценку истинно­го значения величины, найденную путем измерения.
Погрешность результата из­мерения — это разница между результатом измерения X и истин­ным (или действительным) значением измеряемой величины. Она указывает границы неопределенности значения измеряемой ве­личины.
Погрешность средства измерения — разность между по­казанием СИ и истинным (действительным) значением измеряемой ФВ.
Случайная погрешность — составляющая погрешности измере­ния, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, прове­денных с одинаковой тщательностью в одних и тех же условиях.
Систематическая погрешность — составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ.
Прогрессирующая (дрейфовая) погрешность — это непредска­зуемая погрешность, медленно меняющаяся во времени.
Грубая погрешность (промах) -- это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных ре­зультатов этого ряда.

Абсолютная погрешность выража­ется в единицах измеряемой величины.
Относи­тельная погрешность — это отношение абсолютной погрешности из­мерения к истинному значению измеряемой величины.
Приведенная погрешность — это относительная погрешность, в которой абсолютная погрешность СИ отнесена к условно принятому значению , постоянному во всем диапазоне измерений или его части.
Инструментальная погрешность обусловлена погрешностью при­меняемого СИ.
Методическая погрешность возникающая и зависящая от метода измерения.

40. Математические модели и характеристики погрешностей.
Случайным процессом Х(t) называется процесс (функция), зна­чение которого при любом фиксированном значении t = t₀ являет­ся случайной величиной Х(t₀).

Ошибка- Случайная величина.
Математическим ожиданием случайной, функции Х(t) назы­вается неслучайная функция



Здесь р(х,t) — одномерная плотность распределения случайной величины х в соответствую­щем сечении случайного процесса Х(t). Таким образом, математи­ческое ожидание в данном случае является средней функцией, во­круг которой группируются конкретные реализации.
Дисперсией случайной функции Х (t) называется неслучайная функция



значение которой для каждого момента времена равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно mx.
Корреляционная функция — не­случайная функция R(t, t') двух аргументов t и t', которая при каждой паре значений аргументов равна ковариации соответствую­щих сечений случайного процесса.
На практике часто используется нормированная корреляцион­ная функция



Она обладает следующими свойствами:

1. 
   при равенстве аргументов r(t,t) = 1;
   
2. 
   симметрична относительно своих аргументов: r(t,t') = r(t',t;);
   
3. 
   ее возможные значения лежат в диапазоне [-1; 1].
   

Нормированная корреляционная функция по смыслу аналогична коэффициенту корреляции между случайными величинами, но зависит от двух аргументов и не является постоян­ной величиной.

41. Погрешность и неопределенность.
Введен новый термин "неопределенность" — параметр, свя­занный с результатом измерения и характеризующий дисперсию значений, которые могут быть обоснованно приписаны измеряемой величине;

Разделяют неопределенности на два типа: А и В. Вновь вводимые группы неадекватны случайным и систематическим погрешностям. Разделение основано не на теоретических пред­посылках, а на практических соображениях.
Неопределенности типа А могут быть оценены статистически­ми методами на основе многократных измерений и описываются традиционными характеристиками центрированных случайных величин — дисперсией или СКО, Взаимодействие неопределенностей типа А описывается взаимным корреляционным моментом или коэффициентом взаимной корреляции.
Неопределенности типа В могут быть оценены любыми другими методами, кроме статистических. Они должны описываться величинами, аналогичными дисперсии или СКО, так как именно эти ха­рактеристики можно использовать для объединения неопределенностей типа В как между собой, так и с неопределенностями типа А.

42. Правила округления результатов измерений. Оценивание погрешности результата измерения по числу его значащих цифр.
правила округления

1. Погрешность результата измерения указывается двумя зна­чащими цифрами, если первая из них равна 1 или 2, и одной — если первая цифра равна 3 или более.

2. Результат измерения округляется до того же десятичного зна­ка, которым оканчивается округленное значение абсолютной погреш­ности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности,

3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.

4. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

5. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.

6. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.
Абсолютная погрешность, обусловленная округлением



А-первая значащая цифра, S число значащих разрядов.

43. Условия, при которых погрешность измерения может рассматриваться как случайная величина.
факторов:

1. Объект измерения. Перед измерением он должен быть достаточно хорошо изучен с целью корректного выбора его модели. Чем полнее модель соответствует исследуемому объекту, тем точнее могут быть получены результаты измерения. Например, кривизна зем­ной поверхности может не учитываться при измерении площади сельскохозяйственных угодий, так как она не вносит ощутимой погрешности, однако при измерении площади океанов ею пренеб­регать уже нельзя.

2. Субъект измерения. Его вклад в погрешность измерения не­обходимо уменьшать путем подбора операторов высокой квалификации и соблюдения требований эргономики при разработке СИ.

3. Метод и средство измерений. Важен их правильный выбор, который производится на основе априорной информации об объекте измерения. Чем больше априорной информации, тем точнее может быть проведено измерение. Основной вклад в систематиче­скую погрешность вносит, как правило, методическая погрешность.

4. Условия измерения. Обеспечение и стабилизация нормальных условий являются необходимыми требованиями для минимизации дополнительной погрешности, которая по своей природе является систематической.

44. Свойства интегральной и дифференциальной Функций распределения случайной величины.
Интегральной функцией распределения F(х) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина х, в i-м опыте принимает значение, меньшее х:

Свойства:

• неотрицательная, т.е. Р(х) > 0;

• неубывающая, т.е. Р(х_г) > К(х,), если х., > х^

• диапазон ее изменения простирается от 0 до 1, т.е. Р(-°°) => 0;

Р(+) = 1;

• вероятность нахождения случайной величины х в диапазоне от х, до х₂ Р{х₁ < х < х₂} = F(х₂) - P(х,).
дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х) = dF(х)/dх. Она всегда неотрицательна и подчиняется условию нормирования в виде: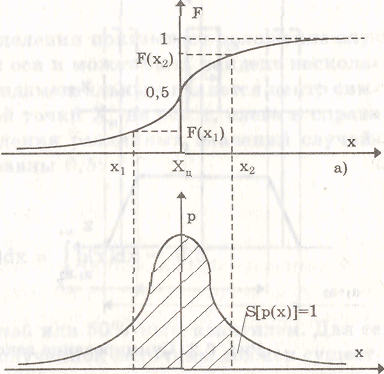

45. Числовые параметры законов распределения. Центр и моменты распределения.
Центр сим­метрии, т.е. нахождение такой точки Х_м на оси X, слева и справа от которой вероятности появления различных значений случай­ной величины одинаковы и равны 0,5. Точку Х_м называют медианой
При симметричной кривой р(х) в качестве центра может ис­пользоваться абсцисса моды., т.е. максимума распределения Х_м
центра сгибов:

Х_г = (х_с)+х_еа)/2,

где х_с], х_с2 — сгибы, т.е. абсциссы точек, в которых распределение достигает своих максимумов.
центра размаха

Х_г = (х+х_еа)/2,
моменты называют начальными, а если от центра рас­пределения, то центральными




Первый начальный момент — МО случайной величины.

Второй начальный момент -



третий начальный момент-

четвертый начальный момент-

эксцесс-

контрэксцесс-

46. Основные классы распределений, используемых в метрологии.

Трапецеидальные распределения

Экспоненциальные распределения

Нормальное распределение

Уплощенные распределения

Распределения Стьюдента

Двумодальные распределения.

47. Экспоненциальное распределение, его свойства и характеристики.
Описывается формулой


При α=1Лапласа, при α=2 Гаусса, при α=∞ Равномерное.

Интегральная функция


Эксцесс


Энтропийный коэффициент

48. Нормальное распределение, его роль в метрологии.
Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса: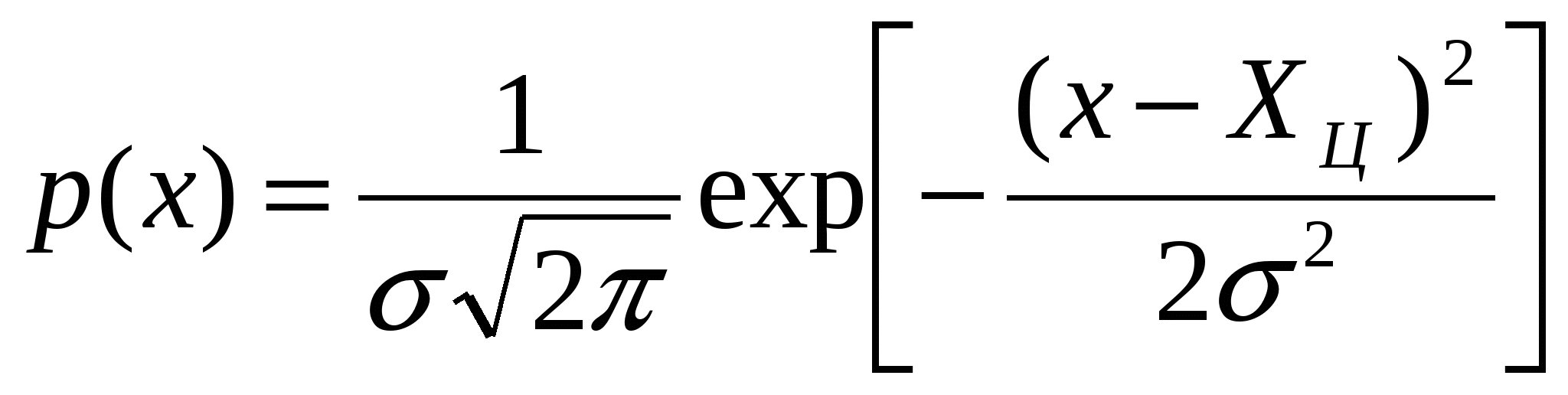



где σ — параметр рассеивания распределения, равный СКО; Хц -центр распределения, равный МО
Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей , утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

49. Функция Лапласа, ее описание и применение.

Определенный интеграл с переменным верхним пределом называют функцией Лапласа. Для нее справедливы следующие равенства: Ф(-∞) = -0,5; Ф(0) = 0; Ф(+∞) = 0,5; Ф(1) = -Ф(1). Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой Р(x) = 0,5+Ф(t). Поскольку интеграл в не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу.

50. Семейство распределений Стьюдента. Его описание и применение.
Распределения Стьюдента нашли широкое применение при статистической обработке результатов многократных

измерений.



где k — число степеней свободы, зависящее от числа п усредняющих отсчетов: k = п-1. При увеличении k с распределение Стьюдента переходит в распределение Гаусса.

При k>4


Свойства

• при п < 3 их СКО становится равным бесконечности, т.е. дисперсионная оценка ширины разброса не работает (перестает существовать);

• классический аппарат моментов для оценки формы и ширины распределения Стьюдента с малым числом степеней свободы оказывается не работоспособным, и их ширина и форма могут быть оценены лишь с использованием доверительных и энтропийных оценок.
Разновидностью распределения Стьюдента является распределение Коши. Оно важно тем, что ему подчиняется распределение отношения двух нормально распределенных центрированных случайных величин. Распределение Коши — это предельное распределение семейства законов Стьюдента с минимально возможным числом степеней свободы, равным К = 1



В общем виде (не нормированном и не центрированном) распре- деление Коши имеет вид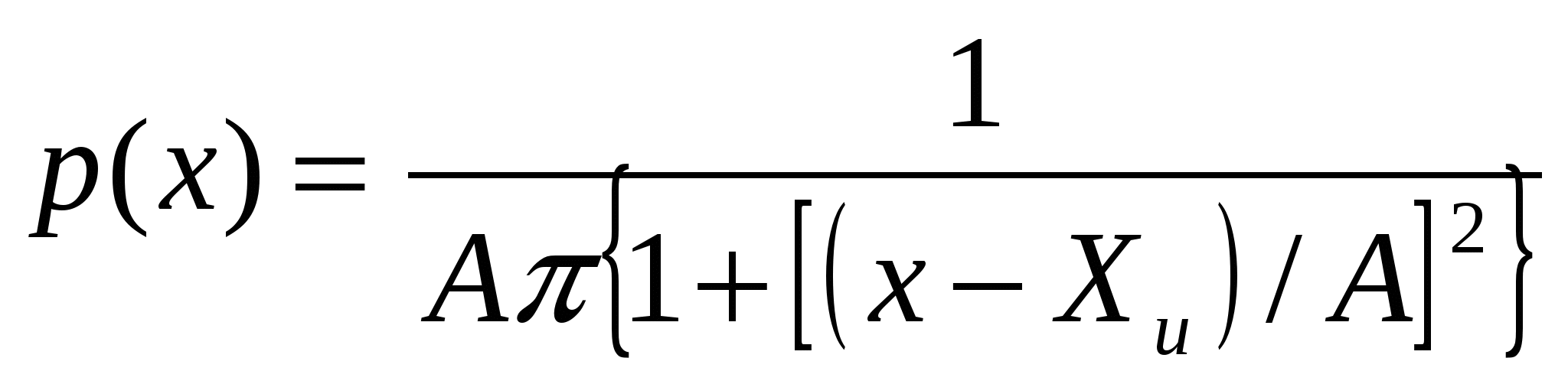



где А, Хц — параметры распределения.

Свойства распределения Коши резко отличаются от свойств экспоненциальных распределений, а именно:

• дисперсия и СКО не существуют, так как определяющий их интеграл расходится. Они будут бесконечно увеличиваться при росте числа экспериментальных данных. Оценка ширины распределения может быть произведена только на основе теории информации;

• оценка центра в виде среднего арифметического для распределения Коши неправомочна, так как ее рассеяние О/л/п равно бес­конечности;

• математическое ожидание не существует;

• для определения Х_ц необходимо использовать медиану;

• эксцесс равен бесконечности, а контрэксцесс равен нулю;

• энтропийное значение погрешности равно 2лА.