Экзаменационные билеты. Экзам. билеты с задачами 2011. Экзаменационный билет 21
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Экзаменационный билет № 21 Классификация движений твердого тела: названия, определения, число степеней свободы и обобщенные координаты, кинематические уравнения движения. Определение числа степеней свободы плоского рычажного механизма. Движение материальной точки под действием восстанавливающей силы, пропорциональной смещению точки от положения равновесия, и силы сопротивления, пропорциональной скорости точки. Построение общего решения дифференциального уравнения движения в зависимости от дискриминанта характеристического уравнения. Исследование свободных затухающих колебаний. Фазовый «портрет» осциллятора с демпфером. Задачи к билету № 21  3. Найти положение центра тяжести снаряда, осевое сечение которого изображено на рисунке справа. 4 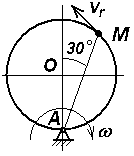 . Диск диаметром 8 см вращается вокруг оси, . Диск диаметром 8 см вращается вокруг оси,перпендикулярной его плоскости и проходящей через точку А, с постоянной угловой скоростью точка М с постоянной относительной скоростью точки М в указанном положении. 5 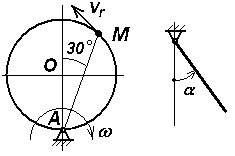 . Однородный тонкий стержень массой 2 кг и длиной . Однородный тонкий стержень массой 2 кг и длиной0,4 м отпускают без начальной угловой скорости из положения, при котором тическую энергию, количество движения стержня и кинетический момент его относительно оси вращения в момент прохождения положения равновесия. 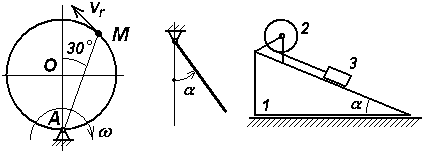 6. Пренебрегая массой нити и трением скольжения, найти ускорение призмы 1 и относительное ускорение тела 3. Массы тел равны призмы равен однородный цилиндр. Экзаменационный билет № 3 Движение свободного твердого тела как результат сложения поступательного и сфериче- ского движений. Мгновенная угловая скорость и мгновенная ось вращения. Скорость точки тела. Вектор бесконечно малого поворота. Вектор бесконечно малого перемещения точки тела. Движение свободного тела как винтовое движение. Интегрирование дифференциального уравнения движения материальной точки в случае, когда сила зависит от времени или постоянна. Задача о прицельном бомбометании. Оп- 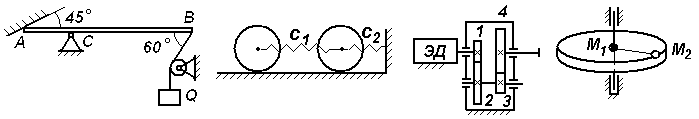 ределение угла вертикальной наводки орудия по координатам цели. ределение угла вертикальной наводки орудия по координатам цели.Задачи к билету № 3 Однородный брус весом равновесии под действием груза весом Найти реакцию опоры А при условии, что АС = 0,2 м, СВ = 0,4 м.  Вал электродвигателя (ЭД) вращается со скоростью 1200 об/мин. Зубчатые колеса имеют соответственно и 5  . Однородный сплошной горизонтальный диск массой . Однородный сплошной горизонтальный диск массой сом диска, когда материальная точка, двигаясь по его радиусу, достигнет положения  Составить дифференциальные уравнения движения колебатель- ной системы, состоящей из двух одинаковых катков, движущих- ся по опорной поверхности без скольжения. Катки представляют собой однородные сплошные диски массой 2 кг. Жесткости пружин Найти также собственные частоты системы. Экзаменационный билет № 20 Вращение твердого тела вокруг неподвижной оси. Кинематическое уравнение движения тела. Определения векторов угловой скорости и углового ускорения. Формулы для расчета векторов скорости, нормального и касательного ускорений точки вращающегося тела в виде векторных произведений. Формулы для расчета модулей этих векторов. Способы интегрирования дифференциального уравнения движения материальной точки в случае, когда сила зависит от скорости точки. Задачи к билету № 20 Тело, подвешенное на пружине, совершает колебания с частотой 10 рад/с. Какой будет частота колебаний, если тело подвесить на трех таких же последовательно соединенных пружинах? 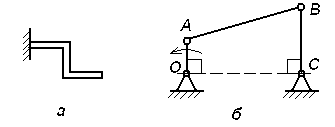 Трехколенный брус заделан в вертикальную стену. Длина каждого колена 2 м. Вес одного погонного метра бруса 1 кН. Найти момент заделки.  Радиусы шестерен 1, 2 и 3 равны соответственно 12 см, 8 см и 4 см. Водило вращается с угловой скоростью низма. Масса водила 3 кг, массы шестерен дисками, водило – однородным стержнем. С оставить, пренебрегая трением скольжения, дифференциальные уравнения движения системы двух тел массами Экзаменационный билет № 8 Законы «сухого» трения Амонтона-Кулона. Задача о страгивании тела с шероховатой поверхности. Угол трения, конус трения. Задача о теле на наклонной шероховатой плоскости. Трение тонкой гибкой нити о шероховатый цилиндр: формула Эйлера. Потенциальное силовое поле: определение и свойства его. Циркуляция и ротор вектора силы. Формулировка свойств поля с использованием символического оператора Гамильтона Задачи к билету № 8  Скорость ползуна А равна 20 см/с и направлена влево. АВ = 10 см, ОВ = ВС. Найти величину и направление скорости точки С рычага ОС. К нижнему концу пружины жесткостью 2000 Н/м, сжатой на 2 см, подвешивают груз массой 2 кг и отпускают его без начальной скорости. Определить движение груза. 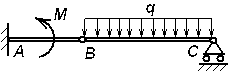 Пренебрегая весом составной балки, определить момент заделки А. Момент активной пары нагрузки 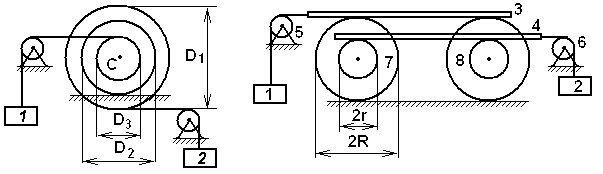 6. Найти ускорение центра масс С катка, катящегося без скольжения по направляющей. Массы грузов равны Масса катка относительно центральной оси равен 12 см. Экзаменационный билет № 7 Центр тяжести (ЦТ) тела: определение ЦТ, формулы для расчета радиус-вектора и декартовых координат ЦТ. ЦТ однородного симметричного тела. ЦТ однородного трехмерного тела, плоской фигуры, нити. Метод отрицательных объемов. Теремы Гюльдена. Элементарная работа силы. Работа силы на «конечном» перемещении как криволинейный интеграл. Выражение для элементарной работы в декартовой системе координат. Мощность силы. Мощность сил, приложенных к вращающемуся твердому телу. Расчет работы по известной мощности сил. Задачи к билету № 7 П 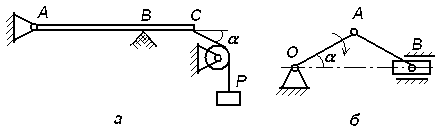 ренебрегая весом балки, найти реакцию ренебрегая весом балки, найти реакцию опоры В. Заданы: вес груза Р, угол α, расстояния Т  рубка в виде кольца радиуса 0,2 м вращается вокруг вертикальной оси АВ с постоянной угловой скоростью 2 рад/с. Внутри трубки движется точка М с постоянной относительной скоростью, равной 0,4 м/с. Найти абсолютное ускорение точки М в позициях рубка в виде кольца радиуса 0,2 м вращается вокруг вертикальной оси АВ с постоянной угловой скоростью 2 рад/с. Внутри трубки движется точка М с постоянной относительной скоростью, равной 0,4 м/с. Найти абсолютное ускорение точки М в позицияхВ и С. 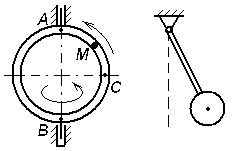 Определить период малых колебаний маятника, состоящего из однородного стержня длиной и массой С  оставить дифференциальные уравнения оставить дифференциальные уравнения движения системы тел и найти ускорения грузов 4 и 5. Катки 3 считать однородными сплошными цилиндрами, качение которых происходит без скольжения. Массы тел: Экзаменационный билет № 16 Вынужденные колебания материальной точки под действием гармонической вынуждающей силы. Построение общего и частного решения. Свободные, сопровождающие и чисто вынужденные колебания. Коэффициент динамичности. АЧХ и ФЧХ колебательного звена системы управления. Вывод формул для моментов инерции однородного стержня (пластины) относительно центральной оси и оси, проходящей через конец стержня. 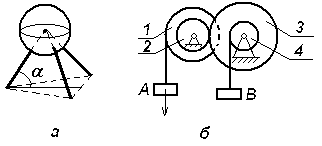 Задачи к билету № 16 Сферическая цистерна весом Р опирается на три стержня, образующие ребра правильной пирамиды. Угол наклона каждого ребра к горизонту равен 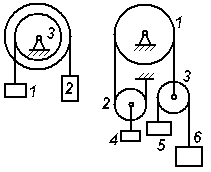 4. Тело массой 0,2 кг бросают со скоростью 4 м/с под углом 4. Тело массой 0,2 кг бросают со скоростью 4 м/с под углом к горизонту. Сила сопротивления меняется по закону где шей точки? Массы тел равны  Ввести обобщенные координаты и составить дифференциальные уравнения движения системы, состоящей из 6 тел. Блоки 1, 2, 3 считать однородными сплошными дисками. Массы тел: Экзаменационный билет № 12 Сила инерции, действующая на материальную точку. Принцип Даламбера. Уравнение кинетостатики. Основное уравнение динамики относительного движения материальной точки. Переносная и кориолисова сила инерции. Исследование малых колебаний физического маятника вблизи положения устойчивого равновесия. Приведенная длина маятника. Центр удара. |
