Экзаменационные билеты. Экзам. билеты с задачами 2011. Экзаменационный билет 21
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
Задачи к билету № 12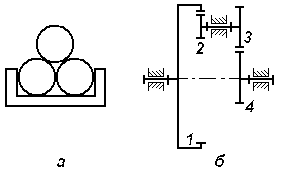 Три одинаковые трубы весом Р каждая уложены в ящик. Найти силы давления верхней трубы на нижние. Из миномета, ствол которого составляет Определить момент инерции однородного сплошного конуса массой С 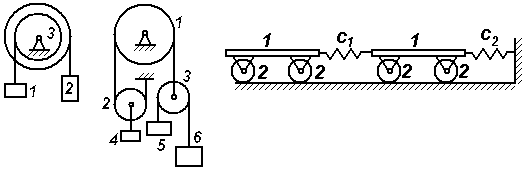 оставить дифференциальные уравнения движения колебательной системы и определить ее собственные частоты. Коэффициенты упругости пружин оставить дифференциальные уравнения движения колебательной системы и определить ее собственные частоты. Коэффициенты упругости пружин Экзаменационный билет № 5 Главный вектор системы сил. Главный момент системы сил относительно заданного полюса. Доказательство равенства нулю главного вектора и главного момента внутренних сил. Равнодействующая системы сил, приложенных к твердому телу. Равновесие материальной точки, механической системы, твердого тела. Вывод уравнений равновесия твердого тела из теорем динамики механической системы. Работа постоянной силы тяжести. Работа силы тяжести, изменяющейся по закону обратных квадратов. Потенциальная энергия тяжелого тела. 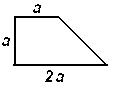 Задачи к билету № 5 Определить положение центра тяжести однородной тонкой пластины в форме трапеции. С  корость ползуна А равна 20 см/с и направлена влево, корость ползуна А равна 20 см/с и направлена влево, АВ = 10 см и ОВ = ВС. Найти величину и направление скорости точки С. Груз массой 2 кг подвешен к нити длиной 2 м, отклоненной на угол груз проходит положение равновесия. 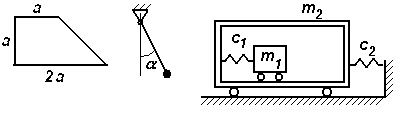 Составить, пренебрегая массами катков, дифференциальные уравнения движения колебательной системы и определить ее собственные частоты. Массы тел Экзаменационный билет № 15 Упругая сила, подчиняющаяся закону Гука. Коэффициенты жесткости и податливости упругих элементов Гука. Расчет эквивалентной жесткости системы элементов Гука при их параллельном и последовательном соединениях. Элементарная работа сил, действующих на твердое тело. Элементарная работа при поступательном и мгновенно-вращательном движениях тела. Работа и мощность сил, приложенных к вращающемуся вокруг неподвижной оси телу. Задачи к билету № 15 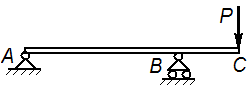 Пренебрегая весом балки, найти реакции опор бруса, если Р=120 Н, Д 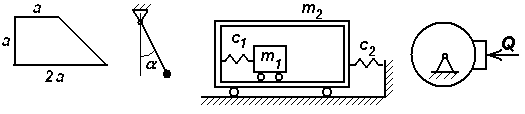 ва груза массами 1 кг и 2 кг висели на пружине неподвижно; при этом пружина была растянута на 10 см по сравнению с ее естественной длиной. В некоторый момент нижний груз массой 2 кг отрывается. Определить движение оставшегося груза. ва груза массами 1 кг и 2 кг висели на пружине неподвижно; при этом пружина была растянута на 10 см по сравнению с ее естественной длиной. В некоторый момент нижний груз массой 2 кг отрывается. Определить движение оставшегося груза.М  аховик в виде сплошного однородного диска массой 6 кг и радиусом 0,2 м вращался с угловой скоростью 20 рад/с. Благодаря прижатию к нему тормозной колодки постоянной силой аховик в виде сплошного однородного диска массой 6 кг и радиусом 0,2 м вращался с угловой скоростью 20 рад/с. Благодаря прижатию к нему тормозной колодки постоянной силой Пренебрегая массами катков и блока, а также силами сопротивления движению, составить дифференциальные уравнения движения механической системы, состоящей из трех тел массами Экзаменационный билет № 22 Основные понятия теоретической механики: материальная точка, механическая система, твердое тело, система отсчета. Свойства пространства и времени, характерные для классической механики. Механическое взаимодействие. Сила; характеристики ее действия. Проявления действия силы. Три раздела теоретической механики. Инерциальные системы отсчета. Акселерометры и гироскопы в летательных аппаратах. Обобщенные активные (задаваемые) силы и обобщенные силы инерции. Общее уравнение динамики механической системы в терминах обобщенных сил. Представление обобщенных сил инерции через производные от кинетической энергии системы. Вывод уравнений Лагранжа второго рода. Задачи к билету № 22 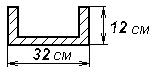 Определить положение центра тяжести сечения швеллера, изготовленного из профиля толщиной 1 см. Т 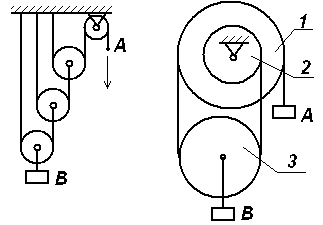 рос, на котором подвешен груз А, охватывает блоки 1 и 3 и намотан на барабан 2, закрепленный на одном валу с блоком 1. Груз А опускается со скоростью 12 см/с. Найти скорость груза В, если диаметр барабана 2 вдвое меньше диаметра блока 1. рос, на котором подвешен груз А, охватывает блоки 1 и 3 и намотан на барабан 2, закрепленный на одном валу с блоком 1. Груз А опускается со скоростью 12 см/с. Найти скорость груза В, если диаметр барабана 2 вдвое меньше диаметра блока 1.Колесо в виде однородного сплошного диска радиусом 20 см катится по горизонтальной направляющей без скольжения, имея в начале движения скорость центра, равную 10 м/с. Какой путь пройдет центр до остановки колеса, если коэффициент сопротивления качению 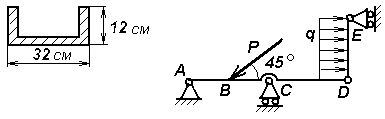 Определить составляющие реакции опоры А. Величина силы Экзаменационный билет № 19 Плоскопараллельное движение твердого тела. Скорость точки плоской фигуры как скорость точки при сложном ее движении. Мгновенный центр скоростей точек плоской фигуры и способы определения его положения. Расчет скорости точки плоской фигуры с помощью построения МЦС. Две основные задачи динамики материальной точки. Описание процесса решения обратной (второй) задачи. Общее и частное решение системы дифференциальных уравнений движения. Определение постоянных интегрирования. Корректность постановки задачи Коши.  Задачи к билету № 19 Однородная балка АВ весом Р = 24 кН закреплена концом В шарнирно, а концом А опирается на гладкую наклонную плоскость. Веревка, привязанная к балке в точке С, несет груз весом  Статическая осадка пружины с чашкой под действием груза М  асса груза 1 равна 2 кг, масса груза 2 равна 1 кг. Масса блока 3, являющегося однородным сплошным цилиндром, равна 6 кг. Определить силы натяжения нитей. асса груза 1 равна 2 кг, масса груза 2 равна 1 кг. Масса блока 3, являющегося однородным сплошным цилиндром, равна 6 кг. Определить силы натяжения нитей.Н  азначить обобщенные координаты и составить дифференциальные уравнения движения механической системы, состоящей из тележек 1 и 2 массами азначить обобщенные координаты и составить дифференциальные уравнения движения механической системы, состоящей из тележек 1 и 2 массами Экзаменационный билет № 23 Векторный способ задания движения точки. Уравнение движения, векторы перемещения, средней и мгновенной скорости, среднего и мгновенного ускорения точки. Направление мгновенной скорости в данной точке траектории. Путь, пройденный точкой за заданный промежуток времени. Связи стационарные и реономные, позиционные и дифференциальные. Голономные механические системы. Обобщенные координаты и обобщенные скорости. Обобщенные задаваемые силы. Обобщенные потенциальные силы. Условия равновесия механической системы в терминах обобщенных сил. Задачи к билету № 23 О  днородный цилиндр весом днородный цилиндр весом  Определить угол вертикальной наводки О   пределить ускорение груза 1 и силу натяжения нити, на которой он подвешен к барабану, закрепленном на одном валу с ведущим шкивом ременной передачи. Барабан считать однородным сплошным цилиндром радиуса пределить ускорение груза 1 и силу натяжения нити, на которой он подвешен к барабану, закрепленном на одном валу с ведущим шкивом ременной передачи. Барабан считать однородным сплошным цилиндром радиуса  Определить опорные реакции составной балки. 2AB = 2BC = 2CD = 2DE = EF = FG. Экзаменационный билет № 24 Естественный способ задания движения материальной точки. Векторное уравнение линии в пространстве. Орты касательной, нормали и бинормали. Соприкасающаяся плоскость. Кривизна и радиус кривизны линии. Эволюта и эвольвента. Естественный трехгранник. Уравнение движения точки по заданной траектории. Проекции скорости и ускорения точки на оси трехгранника. Консервативная механическая система. Функция Лагранжа. Уравнения Лагранжа второго рода для консервативной системы. Консервативные (потенциальные), диссипативные и гироскопические силы. Задачи к билету № 24 О  днородный стержень АВ весом Р = 200 Н закреплен шарнирно в точке А и опирается свободно на опору С. Оттяжка, привязанная к стержню в точке В, несет груз весом Q = 500 Н. На стержень действует пара сил с моментом m = 50 Нм. Определить реакции опор А и В, если АВ = 2 м, ВС = 40 см. днородный стержень АВ весом Р = 200 Н закреплен шарнирно в точке А и опирается свободно на опору С. Оттяжка, привязанная к стержню в точке В, несет груз весом Q = 500 Н. На стержень действует пара сил с моментом m = 50 Нм. Определить реакции опор А и В, если АВ = 2 м, ВС = 40 см.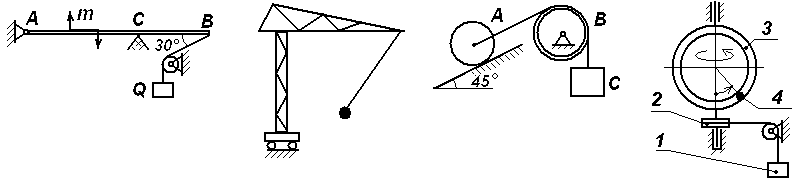 Мостовой кран движется равноускоренно и достигает скорости 2 м/с через 3 с после начала движения. Определить угол отклонения троса, несущего груз, от вертикали при установившемся движении, пренебрегая весом троса. К 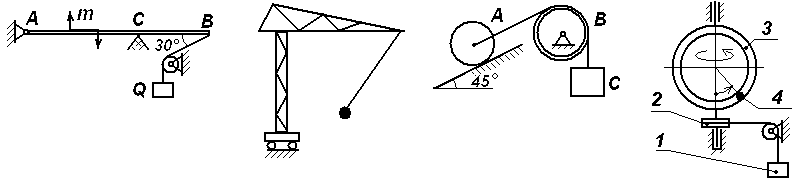 аток А массой аток А массой 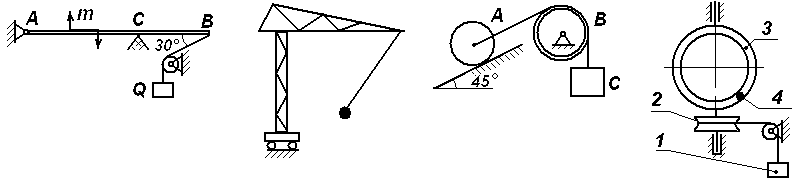 Груз 1 массой |
