Экзаменационные билеты. Экзам. билеты с задачами 2011. Экзаменационный билет 21
 Скачать 0.73 Mb.
|
|
Задачи к билету № 9 Т 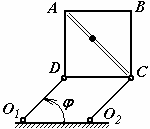 очка М движется по диагонали квадратной плиты АВСDсогласно уравнению  (м). Кривошип  вращается согласно уравнению  . Н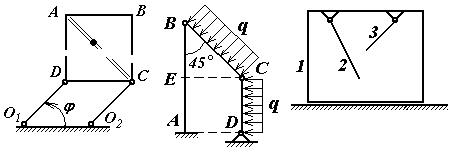айти абсолютное ускорение точки М в момент времени  .  .Г  руз весом 2 кН поднимается вертикально вверх равноускоренно посредством троса. Определить натяжение троса, если известно, что за первые 10 с движения груз поднялся на 8 м.Определить опорные реакции  и  составной балки при условии, что интенсивность распределенной нагрузки  . При этом  . Т ележка 1 массой  скользит по столу без трения. Внутри тележки качаются два однородных стержня 2 и 3 массами  и  , имеющие длину  и  соответственно. Определить собственные частоты малых колебаний системы. Экзаменационный билет № 6 Простейшие передаточные механизмы (зубчатая передача, ременная, цепная передача, передача винт-гайка). Передаточные соотношения между скоростями. Многоступенчатые редукторы угловой скорости. Передаточное число редуктора. Кинематическая схема нереверсивного коаксиального двухступенчатого редуктора. Расчет угловой скорости и вращающего момента на выходном валу при установившемся движении. М 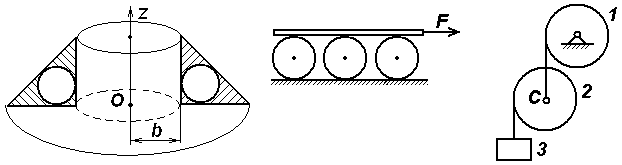 оменты инерции твердого тела относительно полюса, оси и плоскости. Связь между моментами инерции относительно начала декартовой системы координат, координатных осей и плоскостей.Задачи к билету № 6 Найти положение центра тяжести прямоугольного равнобедренного треугольника с круговым вырезом, если длина катета a = 6 см. Найти также объем тела, образованного вращением треугольника вокруг оси  , если  .Начальная скорость камня  . Под каким углом к горизонту следует бросить камень, чтобы он упал на землю на расстоянии 40 м от точки бросания?С тержень массой  лежит на трех одинаковых катках массой  каждый. К стержню приложена постоянная сила  , приводящая в движение стержень и катки. Скольжение между стержнем и катками, а также между катками и опорной плоскостью отсутствует. Определить ускорение стержня. Катки считать однородными сплошными цилиндрами.Определить ускорения центра С тяжести барабана 2 и груза 3. Барабаны 1 и 2 – сплошные диски массой 2 кг каждый. Масса груза 4 кг. Экзаменационный билет № 4 Момент вектора относительно оси, проходящей через заданный полюс. Графоаналитический способ его расчета. Случаи равенства этого момента нулю. Принцип виртуальных (возможных) перемещений для механической системы, подчиненной идеальным связям. Пример. Задачи к билету № 4 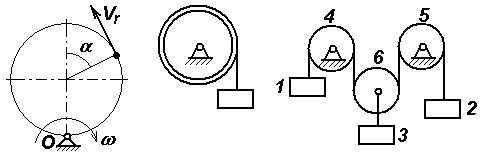 Диск радиуса  вращается вокруг неподвижной оси, проходящей через точку О перпендикулярно плоскости рисунка, с угловой скоростью  . По ободу диска движется точка М с относительной скоростью  . Определить абсолютные скорость и ускорение точки М в момент  , считая угол  .И з пушки, стоящей на башне высотой 50,2 м, вылетает снаряд со скоростью 200 м/с под углом 30º к горизонту. Через какое время и на каком расстоянии от башни снаряд упадет на землю? Сопротивление воздуха в расчет не принимается.На шкив намотана нить, к концу которой прикреплен груз 15 кг. Масса шкива, равная 5 кг, равномерно распределена по его ободу. Радиус шкива 0,95 м. Пренебрегая трением в подшипниках, определить угловое ускорение шкива и натяжение нити. Грузы массами  ,  ,  движутся вертикально. Блоки 4,5,6 – сплошные однородные диски массой 0,5 кг каждый. Определить ускорения грузов.Экзаменационный билет № 2 Момент вектора (например, вектора силы) относительно полюса как векторное произведение. Величина и направление момента. Плечо вектора относительно полюса. Расчет момента вектора относительно начала декартовой системы координат по правилу символического определителя. Моменты относительно координатных осей. Доказательство теоремы об изменении кинетической энергии материальной точки и механической системы. Дифференциальные и интегральная формы записи теоремы.  Задачи к билету № 2 К олесо катится без скольжения по горизонтальной направляющей MN, увлекая стержень АВ, который скользит концом В по той же направляющей. Зная, что в рассматриваемом положении механизма  ,  и , найти скорость точки В, а также угловые скорости звеньев CDи DE . Известно, что  ,  ; соединения A, CиD – шарнирные.К кривошипу приложен вращающий момент М. Какую силу Q надо приложить к ползуну, чтобы уравновесить механизм? ОА = АВ=l;  . Силами трения пренебречь.Три груза соединены нерастяжимой невесомой нитью, причем грузы А и В скользят по гладкой наклонной плоскости, расположенной под углом к горизонту. Определить ускорение грузов и натяжение нити в сечении а – а, если веса грузов  ,  ,  . Одинаковые брусья массой  опираются на катки, представляющие собой однородные сплошные цилиндры. Катки также одинаковы и имеют массу  каждый. Коэффициенты упругости пружин равны  и  . Составить дифференциальные уравнения движения механической системы. Качение брусьев по каткам и катков по опорной плоскости происходит без скольжения. Экзаменационный билет № 1 К 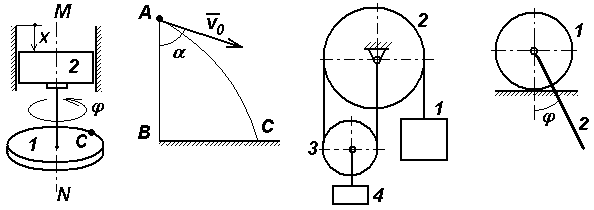 лассификация сил. Внешние и внутренние силы. Главный вектор и главный момент внутренних сил. Понятие о связях в теоретической механике. Активные силы и реакции связей. Примеры реакций отдельных видов связей. Общее уравнение динамики системы. Пример применения для решения задачи №5. Задачи к билету № 1 Горизонтально расположенный диск 1 радиусом  совершает крутильные колебания вокруг вертикальной оси MN по закону  . Плита 2, на которой закреплен верхний конец упругой проволоки, движется между вертикальными направляющими по закону  . Определить абсолютную скорость и абсолютное ускорение точки С диска в момент . (24) Груз, сброшенный с пикирующего самолета в точке А на высоте АВ = h, имеет начальную скорость  , составляющую угол  с вертикалью. На каком расстоянии S = BC груз упадет на землю? Сопротивлением воздуха пренебречь. (14) Массы грузов 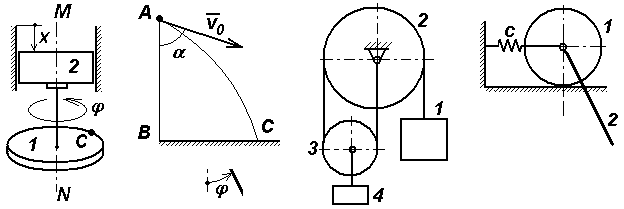 ,  ; массы блоков  и . Блоки представляют собой однородные сплошные диски. Определить ускорения грузов и натяжения нитей, несущих эти грузы. (23) Каток 1 массой , соединенный со стенкой пружиной жесткостью с = 400 Н/м, движется без скольжения по неподвижной направляющей. С катком шарнирно связан однородный стержень 2 массой  и длиной  . Определить собственные частоты малых колебаний системы. (34)Экзаменационный билет № 26 Доказательство теоремы Гюйгенса-Штейнера о моментах инерции тела относительно двух параллельных осей, одна из которых – центральная. Функциональные пространства. Примеры. Нормы в функциональных пространствах. Скалярное произведение элементов пространства. Функционал; условие стационарности функционала. Вариационный принцип Гамильтона-Остроградского. Вывод уравнений Лагранжа второго рода из принципа Гамильтона. 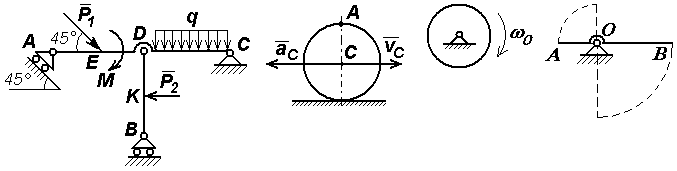 Задачи к билету № 26 Колесо радиуса 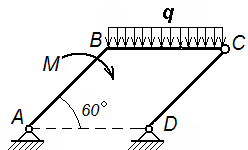 катится без скольжения, имея в некоторый момент времени скорость центра  и ускорение центра  . Определить в этот момент ускорение точки А. О  днородный стержень начинает вращаться вокруг оси О из состояния покоя из горизонтального положения. Найти его угловую скорость в вертикальном положении. OB = 2OA = 2l.На составную балку действует распределенная нагрузка интенсивностью  и пара сил с моментом  . Определить реакцию опоры А, если АB = BC =CD = DA = l.Н  айти собственные частоты механической системы, содержащей грузы массами m=1кг , связанные друг с другом и со стойкой элементами Гука, имеющими жесткость с=400Н/м. Трением скольжения пренебречь. В положении равновесия пружины не деформированы. Экзаменационный билет № 27 Главный вектор и главный момент плоской системы сил. Система уравнений равновесия (три её формы). Графо-аналитический расчет момента силы относительно полюса в плоской задаче статики. Статически определенные и статически неопределенные задачи. Структура выражения для кинетической энергии как функции обобщенных координат и скоростей при стационарных связях. Разложение в ряд Тейлора кинетической и потенциальной энергии в окрестности положения устойчивого равновесия консервативной механической системы. Составление дифференциальных уравнений малых колебаний системы вблизи этого положения. Матричная запись системы уравнений. Вековое (частотное) уравнение. |