Экзаменационные билеты. Экзам. билеты с задачами 2011. Экзаменационный билет 21
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Экзаменационный билет №17 Решение задачи о теле, брошенном под углом к горизонту. Определение угла вертикальной наводки орудия по координатам цели. Центр масс механической системы: определение, формулы для расчета его декартовых координат. Выражение количества движения механической системы через скорость центра масс. Задачи к билету № 17 Г 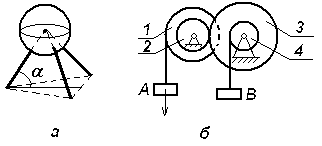 руз А опускается со скоростью руз А опускается со скоростью равны 4. Материальная точка массой к центру О силой момент находилась в покое на расстоянии 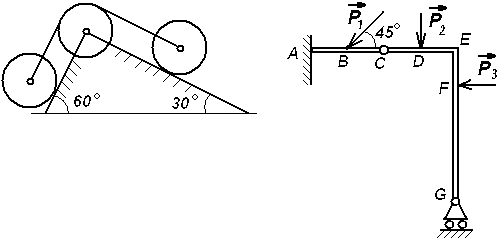 нии нии К  атки и блок представляют собой одинаковые сплошные однородные цилиндры массой атки и блок представляют собой одинаковые сплошные однородные цилиндры массой Определить момент заделки А и реакию опоры G, если Экзаменационный билет №18 Вывод формул моментов инерции однородного тонкого обруча (трубы) и однородного диска (цилиндра) относительно центральных осей инерции. К 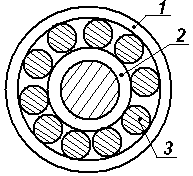 оличество движения материальной точки и механической системы. Теорема об изменении количества движения точки и системы в дифференциальной и интегральной форме. Закон движения центра масс. оличество движения материальной точки и механической системы. Теорема об изменении количества движения точки и системы в дифференциальной и интегральной форме. Закон движения центра масс.Задачи к билету № 18 Кольцо 1, внутренний диаметр которого 8 см, вращается по часовой стрелке с угловой скоростью 20 рад/с. Кольцо 2, имеющее наружный диаметр 4 см, вращается на валу против часовой стрелки с угловой скоростью 10 рад/с. Найти скорость центра сечения ролика 3, а также угловую скорость ролика. В результате обрыва минрепа морская мина начинает всплывать с глубины 90 м. Сила сопротивления воды равна П 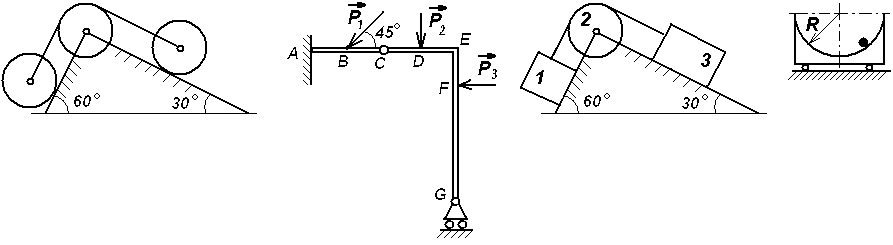 ренебрегая силами трения грузов 1 и 2 о наклонные плоскости и считая блок 3 однородным диском, определить силы натяжения нитей. Массы тел равны ренебрегая силами трения грузов 1 и 2 о наклонные плоскости и считая блок 3 однородным диском, определить силы натяжения нитей. Массы тел равны С  оставить дифференциальные уравнения движения механической системы, состоящей из тележки массой оставить дифференциальные уравнения движения механической системы, состоящей из тележки массой Экзаменационный билет №14 Явление резонанса в вынужденных колебаниях. Построение резонансного решения дифференциального уравнения вынужденных колебаний при гармонической вынуждающей силе. Биения. Кинетический момент материальной точки и механической системы относительно полюса и относительно оси. Доказательство теоремы об изменении кинетического момента материальной точки. 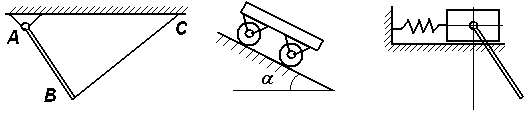 Задачи к билету № 14 Однородный брус АВ весом 600 Н закреплен шарнирно в токе А и подвешен на веревке ВС . Найти реакцию опоры А и силу натяжения веревки, если АВ = 3м, ВС = 4м, АС = 5м. 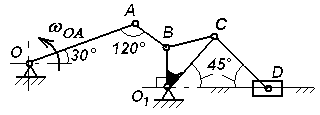 Рычаг ОА длиной 20 см имеет угловую скорость 3 рад/с. Определить величину и направление скорости точки D, если  Определить ускорение шасси тележки, имеющей четыре колеса и скатывающейся по наклонной плоскости, которая составляет угол  Составить дифференциальные уравнения малых колебаний механической системы, включающей в себя ползун массой 4 кг и однородный стержень массой 6 кг, закрепленный шарнирно на ползуне. Жесткость пружины составляет 600 Н/м. Длина стержня 0,6 м. Экзаменационный билет № 13 Прямолинейное движение материальной точки под действием восстанавливающей силы, пропорциональной смещению из положения равновесия. Общее и частное решения дифференциального уравнения свободных незатухающих гармонических колебаний. Круговая частота и период колебаний. Амплитуда и начальный сдвиг по фазе колебаний; их определение из начальных условий. График движения. Фазовый «портрет» гармонического осциллятора без демпфера. Кинетический момент вращающегося твердого тела относительно оси вращения. Динамическое уравнение вращательного движения. Задачи к билету № 13 О 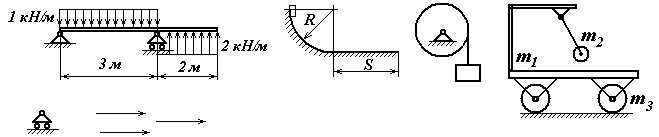 пределить опорные реакции, действующие пределить опорные реакции, действующие на невесомый брус. Т  ело малых размеров спускается без начальной скорости по глад- ело малых размеров спускается без начальной скорости по глад-  кой цилиндрической поверхности, представленной на рис.в виде четверти окружности радиуса кой цилиндрической поверхности, представленной на рис.в виде четверти окружности радиуса На барабан радиуса Т  ележка массой ележка массой Экзаменационный билет № 11 Интегрирование дифференциального уравнения движения материальной точки в случае действия силы, зависящей от положения точки. Интеграл энергии. Кинетический момент твердого тела, совершающего сферическое движение. Понятие о тензоре (матрице) инерции тела. Осевые и центробежные моменты инерции. Главные и центральные оси инерции.  Задачи к билету № 11 Задачи к билету № 11Определить реакции заделки, если интенсивность распределенной нагрузки, действующей на невесомый брус, равна 2 кН/м, а величина сосредоточенной силы  В положении механизма, изображенном на рис., скорость крайней справа точки колеса О  пределить закон колебаний груза по гладкой плоскости, наклоненной к горизонту под углом пределить закон колебаний груза по гладкой плоскости, наклоненной к горизонту под углом О  пределить ускорения грузов и натяжение нити в сечении а-а, если массы тел равны пределить ускорения грузов и натяжение нити в сечении а-а, если массы тел равны Экзаменационный билет № 10 Сложение вращений твердого тела вокруг пересекающихся осей. Теорема о сложении угловых скоростей. Мгновенная ось вращения. Сферическое движение тела как сложное вращение. Углы Эйлера. Скорость и ускорение точки тела при его сферическом движении. Обобщенные координаты и обобщенные скорости голономной мех. системы. Обобщенные задаваемые силы. Обобщенные потенциальные силы. Принцип виртуальных перемещений в терминах обобщенных сил. 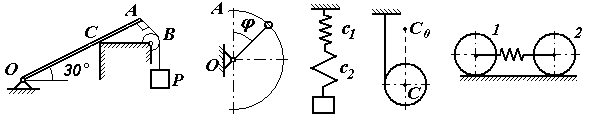 Задачи к билету № 10 Задачи к билету № 10О 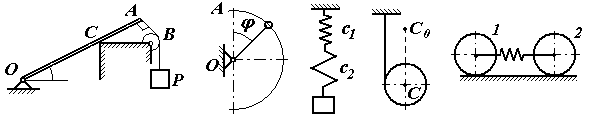 днородная балка ОА весом днородная балка ОА весом Тяжелая отливка малого размера прикреплена к невесомому стержню, который может вращаться вокруг неподвижной оси О. Отливка падает с ничтожно малой скоростью из положения А. Определить величину угла 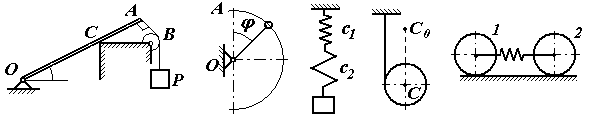 Барабан с намотанной на него нитью опускается из состояния покоя, раз- матывая нить. Считая барабан однородным сплошным цилиндром, опре- делить скорость его оси С в зависимости от пути точками оси с начала движения. Д 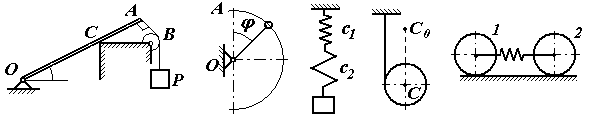 ва одинаковых колеса массами ва одинаковых колеса массами Экзаменационный билет № 9 Сопротивление качению колеса по неподвижной направляющей. Приведение множества сил реакций направляющей к основанию вертикального диаметра и к равнодействующей. Момент сопротивления качению. Геометрическая интерпретация коэффициента сопротивления качению. Теоремы Кёнига о кинетической энергии и кинетическом моменте. |
