Экзаменационные билеты. Экзам. билеты с задачами 2011. Экзаменационный билет 21

• Название: Экзаменационный билет 21
• Анкор: Экзаменационные билеты
• Дата: 14.06.2022
• Размер: 0.73 Mb.
• Имя файла: Экзам. билеты с задачами 2011.doc
• Тип: Документы; #591025
• страница: 5 из 5

Задачи к билету № 27

3. 
   К олесо радиуса катится без скольжения по горизонтальной плоскости. Стержень АВ соединен шарнирно с колесом в точке В и движется так, что его конец А скользит по плоскости. Определить угловую стержня и скорость его конца А в положении, изображенном на рис., если в этом положении скорость центра равна и направлена вправо, АС = 30 см.
   
4. 
   К концу пружины жесткостью 0,1 Н/см подвешен груз весом 2 Н. В начальный момент времени груз находился в положении равновесия и получил некоторую начальную скорость . Зная, что амплитуда колебаний груза равна 2 см, определить величину начальной скорости.
   
5. 
   С оставная балка находится в равновесии под действием пары сил с моментом М = 2 кНм, сосредоточенной силы Р = 4 кН и распределенной нагрузки с интенсивностью q = 1 кН/м. ОА = ВС =4 м, , .Определить реакцию опоры С.
   

6. 
   К атки 2 и 4 катятся без скольжения по клину 1. Клин скользит, не испытывая сопротивления, по горизонтальной поверхности. Масса клина , массы катков и блоков, представляющих собой однородные сплошные цилиндры, одинаковы: . Найти ускорение клина.
   

Экзаменационный билет № 28

1. 
   Вывод формул для кинетической энергии твердого тела при его поступательном, вращательном и плоскопараллельном движениях. Кинетическая энергия тела при сферическом движении. Кинетическая энергия свободного твердого тела.
   
2. 
   Устойчивость положения равновесия и движения механической системы. Асимптотически устойчивое положение равновесия. Теорема Лагранжа-Дирихле об устойчивости изолированного положения равновесия.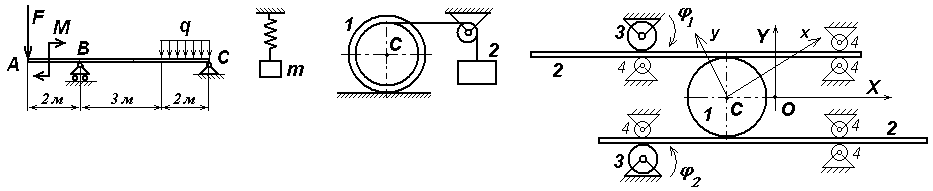
   

Задачи к билету № 28

3. 
   Однородная балка АС весом Р = 4 кН лежит на двух опорах. На балку действует сила F = 8 кН, пара сил с моментом М = 6 кНм и распределенная нагрузка интенсивностью q = 1 кН/м. Определить реакции опор В и С.
   
4. 
   В ерхний конец пружины прикреплен к потолку, а к нижнему концу прикреплен груз массой . Пружина такова, что ее длина в недеформированном состоянии равна 0,2 м, а при равновесии груза составляет 0,24 м. В начальный момент времени пружина была растянута до длины 0,22 м, и груз был отпущен без начальной скорости. Определить движение груза.
   

5. 
   На вал катка 1 массой н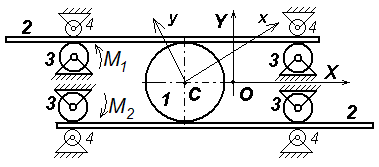амотана нить, переброшенная через небольшой блок и несущая на конце груз 2 массой . Радиус вала , радиус катка . Радиус инерции катка с валом относительно центральной оси, перпендикулярной плоскости рисунка, равен . В начальный момент система покоилась. Определить скорость центра С катка в тот момент, когда груз опустился на высоту , а также ускорение груза.
   
6. 
   П яльцы вышивального автомата крепятся к колесу 1, которое приводится в движение благодаря фрикционной связи с зубчатыми рейками 2. Рейкам движение сообщается от ведущих зубчатых колес 3, которым от шаговых электродвигателей (ШД) сообщаются вращающие моменты M₁ и M₂. Масса колеса 1 вместе с пяльцами равна , центр масс этого тела находится в точке С, момент инерции этого тела относительно оси Cz равен . Приведенная масса каждой рейки равна (с учетом инерционности направляющих роликов 4, зубчатых колес 3, соединительной муфты и вала ШД). Радиусы колес 1 и 3 равны соответственно Rи r. Составить дифференциальные уравнения движения механизма.
   

Экзаменационный билет № 25

1. 
   Сложное движение точки. Абсолютная, переносная и относительная скорость (и ускорение) точки. Доказательство теорем о сложении скоростей и ускорений при поступательном и вращательном движении подвижной системы отсчета.
   
2. 
   Принцип Даламбера для механической системы. Главный вектор и главный момент сил инерции, приложенных к твердому телу. Уравнения кинетостатики твердого тела.
   

Задачи к билету № 25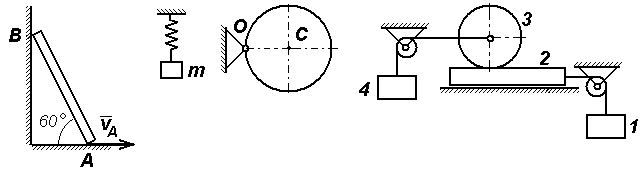

3. 
   Стержень АВ длиной 0,5 м движется, скользя концом А по полу, а концом В – по столу. Определить скорость и ускорение точки В, если точка А движется с постоянной скоростью .
   

4. 
   Г руз массой подвешен на пружине, которая в естественном состоянии имеет длину 40 см. Статическое удлинение пружины под действием данного груза равно 4 см. Груз подвесили к пружине, сжатой до длины 12 см и отпустили без начальной скорости. Определить движение груза.
   

5. 
   О днородный сплошной диск радиуса Rможет вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рис. Диск отпускают из состояния покоя из положения, в котором отрезок ОС горизонтален. Найти скорость центра С диска в тот момент, когда он проходит положение равновесия.
   

6. 
   Груз 1 приводит в движение брус 2, который скользит без трения по горизонтальной плоскости. По брусу катится без скольжения каток 3, связанный нитью с грузом 4. Найти ускорения грузов, если массы тел соответственно равны .
   

Экзаменационный билет № 29

1. 
   Виртуальные (возможные) перемещения точек голономной механической системы. Понятие о вариации функции (функционала). Идеальные связи.
   
2.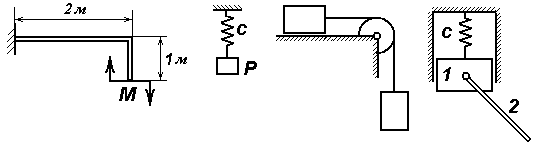 
   У дар материальной точки о неподвижную преграду. Коэффициент восстановления. Абсолютно упругий и абсолютно неупругий удар. Прямой удар двух тел. Расчет скоростей тел после удара.
   

Задачи к билету № 29

3. 
   Балка сварена из двух кусков однородного стержня. Погонный вес одного метра стержня равен 2 кН. Определить реакцию заделки.
   

4. 
   Гиря весом Р = 10 Н подвешена на пружине, верхний конец которой закреплен. Коэффициент упругости пружины с = 100 Н/м. Определить движение гири, если ее подвесили к пружине, сжатой на 5 см, и отпустили без начальной скорости.
   

5. 
   Два груза весом Р = 50 Н каждый соединены нитью, переброшенной через невесомый блок. Коэффициент трения верхнего груза о горизонтальную опорную плоскость . В начале движения грузы находятся в покое. Определить скорость г рузов в тот момент, когда нижний груз опустится на высоту . Найти также их ускорение и натяжение нити.
   

6. 
   М асса ползуна 1 , масса однородного стержня 2 , длина стержня . Жесткость пружины . Определить собственные частоты малых колебаний системы.
   

Экзаменационный билет № 30

1. 
   Вариационные и невариационные принципы механики. Дифференциальные и интегральные принципы. Принципы Лагранжа, Гаусса, Журдена.
   
2. 
   Расчет ударных реакций вращающегося тела на ось вращения. Центр удара.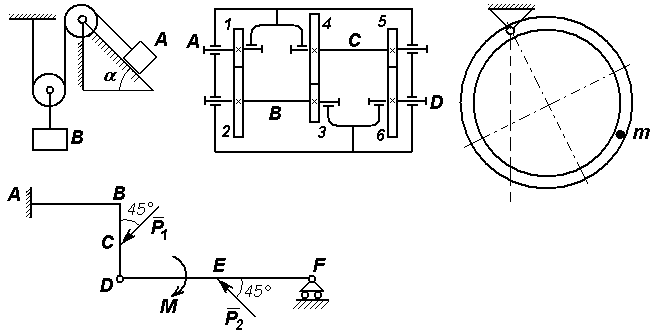
   

Задачи к билету № 30

3. 
   Определить опорные реакции составной балки при следующих условиях: AB = BD = DE = EF = 2 м; ВС = CD; М = 6 кНм; .
   

4. 
   З убчатые колеса редуктора имеют следующие числа зубцов: , . Быстроходный вал А вращается равномерно с угловой скоростью под действием приложенного к нему вращающего момента Определить угловую скорость тихоходного вала В и вращающий момент на этом валу, если к.п.д. зубчатых передач .
   
5. 
   Тело А массой движется по наклонной плоскости, поднимая при этом груз В массой . Коэффициент трения тела А о наклонную плоскость f = 0,2. Каждый блок представляет собой сплошной диск массой Угол наклона плоскости к горизонту . Определить ускорение тела А.
   

6. 
   В нутри тонкого кольца массой М и радиусом R, качающегося вокруг горизонтальной оси, движется маленький шарик массой m. Определить собственные частоты малых колебаний системы.