Правовая статистика. ПС зачет. 1. Статистика как отрасль науки. Ее предмет, задачи, система. Статистика отрасль
 Скачать 186.07 Kb. Скачать 186.07 Kb.
|
|
31. основные правила построения группировок. Вторичная группировка Построение статистических группировок осуществляется по следующим этапам: 1. Определение группировочного признака. 2. Определение числа групп. 3. Расчёт ширины интервала группировки. 4. Определение признаков, которые в комбинации друг с другом будут характеризовать каждую выделенную группу. Построение группировки начинается с определения группировочного признака. Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования. В качестве основания группировки необходимо использовать существенные, теоретически обоснованные признаки. В основание группировки могут быть положены как количественные, так и качественные признаки. Количественные признаки – это признаки, которые имеют числовое выражение (объём выпускаемой продукции, возраст человека, доход сотрудника фирмы и т. д.). Качественные признаки отражают состояние единицы совокупности (пол, отраслевая принадлежность предприятия, форма собственности фирмы и т.д.). Вторичная группировка — образование новых групп на основе ранее осуществленной группировки. Получение новых групп на основе имеющихся возможно двумя способами: объединением первоначальных интервалов (путем их укрупнения) и долевой перегруппировкой (на основе закрепления за каждой группой определенной доли единиц совокупности). Вторичные группировки используют, когда имеющиеся группировки не удовлетворяют требованиям анализа — несопоставимы из-за различного числа выделенных групп или неодинаковых границ интервалов. К этому методу прибегают также в тех случаях, когда в результате первоначальной группировки нечетко проявился характер распределения изучаемой совокупности. 32. Классификация преступлений по уголовно-правовым признакам -преступлениями небольшой тяжести признаются умышленные и неосторожные деяния, за совершение которых максимальное наказание, предусмотренное настоящим Кодексом, не превышает трех лет лишения свободы. -средней тяжести признаются умышленные деяния, за совершение которых максимальное наказание, предусмотренное настоящим Кодексом, не превышает пяти лет лишения свободы, и неосторожные деяния, за совершение которых максимальное наказание, предусмотренное настоящим Кодексом, не превышает десяти лет лишения свободы. -тяжкими преступлениями признаются умышленные деяния, за совершение которых максимальное наказание, предусмотренное настоящим Кодексом, не превышает десяти лет лишения свободы, и неосторожные деяния, за совершение которых максимальное наказание, предусмотренное настоящим Кодексом, не превышает пятнадцати лет лишения свободы. -особо тяжкими преступлениями признаются умышленные деяния, за совершение которых настоящим Кодексом предусмотрено наказание в виде лишения свободы на срок свыше десяти лет или более строгое наказание. В Особенной части УК РФ преступления распределяются в зависимости от объекта посягательства — родового (деление Особенной части УК РФ на разделы) и видового (деление разделов Особенной части УК РФ на главы). В зависимости от формы вины все преступления подразделяются на умышленные и неосторожные. 33. Классификация личности преступника по уголовно-правовым и демографическим признакам - социологических (социально-демографических) - правовых. К первой из них относятся: *пол. Среди преступников значительно больше мужчин, чем женщин. Однако в некоторых видах преступлений доля женщин выше. *Возраст. Лица молодежного возраста чаще совершают преступления агрессивного, импульсного характера. Возраст во многом определяет потребности, жизненные цели людей, круг их интересов, образ жизни, что не может не сказываться на противоправных действиях. Часто совершают преступления лица в возрасте 14–24 лет, в целом же преступники чаще всего принадлежат к возрастной группе до 29 лет. 30–39 лет, а затем преступная активность значительно спадает. Основная масса таких преступлений, как убийства, нанесение тяжких телесных повреждений, кражи, грабежи, разбои, хулиганство, изнасилования, совершается лицами до 30 лет. *уровень образования. Уровень образования лиц, совершающих преступления, ниже, чем у других граждан, причем особенно низка доля лиц, имеющих высшее и среднее специальное образование. Самый низкий уровень образования у лиц, совершающих насильственные, корыстно-насильственные преступления и кражи личного имущества. Выше уровень образования у тех лиц, совершающих хищения путём присвоения и растрат, злоупотребление служебным положением, должностные и экономические преступления. *социальное положение. Данные о социальном положении и роде занятий лиц, совершивших преступления, позволяют сделать выводы о том, в каких социальных слоях и группах, в каких сферах жизнедеятельности наиболее распространены те или иные преступления. *наличие семьи. Половина преступников к моменту совершения преступления не состояла в браке, что значительно выше доли не состоявших в браке среди всего населения. Около половины всех преступников холостые (не замужем). Брак, семья являются значительным моральным и социальным стабилизирующим фактором. Напротив, распад семьи, разлука с детьми вследствие осуждения женщин к лишению свободы приводит к безнадзорности детей. *уровень материальной обеспеченности, социальное происхождение, занятость общественно полезным трудом, род занятий, наличие специальности, место жительства. Ко вторым - характер, степень тяжести совершенных преступлений, совершение преступлений впервые или повторно, в группе или в одиночку, длительность преступной деятельности, объект преступного посягательства, форма вины. 34. Вариация статистических признаков: понятие, виды Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Виды вариаций: 1. Альтернативная - это вариация, при которой изучаемый признак принимает только одно из двух значений, противоположных по своей сути. 2. Систематическая - это изменение признака в определенном направлении. 3. Случайная - вариация, не имеющая явно выраженного направления, т.е. изменчивость признака непредсказуема. 35. ряды распределения: понятие, виды, элементы ряда распределения Ряд распределения – это ряд чисел, характеризующий распределение единиц изучаемой совокупности по какому-либо признаку, причем значения признака расположены упорядоченно – в порядке возрастания либо убывания. Ряды распределения подразделяются на следующие виды: · атрибутивные ряды распределения; · вариационные ряды распределения. Атрибутивные ряды распределения образованы по атрибутивным, то есть качественным, признакам. Например, распределение населения по полу, по образованию и т.д. В атрибутивном ряду образуется столько групп, сколько наименований имеет данный атрибутивный признак. Например, в распределении населения по полу возможны только два типа признака: мужской и женский пол. Вариационные ряды распределения образуются по количественному признаку. В вариационном ряду различают два элемента: варианты и частоты. Варианта – это отдельное значение признака в вариационном ряду. Варианты показываются в первой графе таблицы. Частота – это число, показывающее, как часто повторяется та или иная варианта. Значений частот столько, сколько вариант в данном ряду. Каждой варианте соответствует своя частота. Различают такие вариационные ряды распределения: · дискретные; · интервальные. В дискретных вариационных рядах признак изменяется прерывно, принимает отдельные целые значения. В интервальных вариационных рядах значения вариант задаются в виде интервалов 36. Характеристика ряда распределения Ряд распределения — группировка, в которой для характеристики групп применяется один показатель — численность группы, т.е. это ряд чисел, показывающий, как распределяются единицы совокупности по изучаемому признаку. Атрибутивные ряды распределения — ряды, построенные по атрибутивному признаку. Атрибутивный ряд распределения содержит три элемента: разновидности атрибутивного признака; численность единиц в каждой группе — частоты ряда распределения; численности групп, выраженные в долях (процентах) от общей численности единиц, — частости. Сумма частостей равна единице, если они выражены в долях единицы, и 100%, если они выражены в процентах. Вариационные ряды распределения — ряды, построенные по количественному признаку. Числовые значения количественного признака в вариационном ряду распределения называются вариантами и располагаются в определенной последовательности. Варианты могут выражаться числами — положительными и отрицательными, абсолютными и относительными. Вариационные ряды делятся на дискретные и интервальные. Дискретные вариационные ряды характеризуют распределение единиц совокупности по дискретному (прерывному) признаку, т.е. принимающему целые значения. Частоты в дискретном вариационном ряду, как и в атрибутивном, могут быть заменены частостями. В случае непрерывной вариации величина признака может принимать любые значения в определенном интервале. Интервальные (непрерывные) вариационные ряды строятся на принципах статистической группировки. При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала. 37. показатели вариации и способы их вычисления Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям относятся: ─ размах вариации, Размах вариации (R) вычисляется как разность между наибольшим и наименьшим значениями варьирующего признака Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое (хmin) и самое большое значение признака (хmax). Например, различие между максимальной и минимальной пенсией отдельных групп населения, уровнем дохода различных категорий работающих или нормами выработки у рабочих определенной специальности или квалификации. Размах является важной характеристикой вариации, он дает первое общее представление о различии единиц внутри совокупности. Размах вариации выражается в тех именованных числах, в каких выражены значения признака. ─ среднее линейное отклонение, Показатель размаха вариации дает обобщающую характеристику только границам (амплитуде) значений признака, но не дает характеристики вариации распределению отклонений 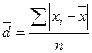 ─ дисперсия ─ среднее квадратическое отклонение. К относительным показателям вариации относятся: ─ коэффициент вариации, ─ относительное линейное отклонение и др. 38. приемы анализа вариационных рядов Закономерные изменения частот за счет изменения варьирующего признака в вариационных рядах называется закономерностями распределения. Главной задачей анализа вариационных рядов является выявление закономерностей распределения и характера распределения. Например, распределение рабочих по уровню заработной платы зависит от условий: - квалификации; - нормы выработки; - расценок; - условий труда – это общее условие. Тип закономерности распределения – это отражение в вариационных рядах общих условий, определяющих распределение в однородной совокупности. Общие условия, определяющие тип закономерностей, познаются анализом сущности явления тех его свойств и условий, которые определяют изменчивость вариационного признака. Следовательно, должна быть построена кривая распределения. Кривая распределения – это графическое изображение частот варьирующего ряда в виде непрерывной линии, где частоты связаны с вариантами функционально. Существует теоретическая кривая распределения и фактическая. Теоретическая кривая выражает общую закономерность данного распределения в чистом виде исключающую влияния случайных условий. Рис. 4. Полигон распределения Полигон распределения – непрерывная линия, характеризующая фактическую кривую распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение. В экономической статистике кривая нормального распределения (рис. 5) встречается достаточно редко, но нормальное распределение может служить моделью для выяснения степени и характера отклонения от нее фактического распределения.  Рис. 5. Кривая нормального распределения Выравнивание фактического распределения по кривой нормального распределения. Cостоит из нескольких этапов: - сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения; - проверяют на сколько распределение признака соответствует нормальному.  39. графическое представление ряда распределения Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения. Для графического изображения дискретного вариационного ряда используется полигон частот (или полигон относительных частот). Для его построения в прямоугольной системе координат на оси абсцисс отмечают точки, соответствующие величине вариантов значений признака, а на оси ординат соответствующие этим вариантам частоты (относительные частоты). Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот (полигоном относительных частот) (рис. 11). Пример. Построить полигон частот, используя данные табл. 3. 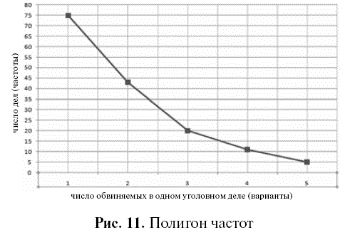 Для графического изображения интервальных вариационных рядов применяется гистограмма. Гистограммой называют графическое изображение зависимости частоты вариантов значений признака от соответствующего интервала группировки. Подчеркнем, что в качестве ординаты здесь берется не сама частота, а частота, деленная на длину интервала группировки. Если все интервалы группировки имеют одинаковую длину, деление на длину интервала обычно опускают и частоты используют как ординаты. 40. абсолютные величины Абсолютные величины- исходная, первичная общая форма выражения статистических показателей характеризующая объем совокупности, т.е. число единиц Виды: Индивидуальные – отражают размеры количественных признаков у отдельных единиц изучаемой совокупности. Общие – выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом. Абсолютные величины являются основой для расчета разных относительных статистических показателей. Абсолютные статистические величины показывают объем, размеры, уровни различных социально-экономических явлений и процессов. Они отражают уровни в физических мерах объема, веса и т.п. В общем абсолютные статистические величины – это именованные числа. 41. Относительные величины, их виды и применение в правовой статистике. Относительная величина (показатель) представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Относительными величинами в статистике называются обобщающие показатели. В статистике относительные показатели используют в сравнительном анализе, в обобщении. Относительные показатели могут выражаться в коэффициентах, процентах, милле, промилле, продецимилле или быть именованными числами. Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000, то относительный показатель соответственно выражается в процентах (%), промилле (‰) и т.д. В зависимости от целей статистического анализа различают следующие виды показателей в форме относительных величин: 1. относительный показатель плана характеризует относительную высоту планового уровня, т.е. во сколько раз, намечаемый объемный показатель превысит достигнутый уровень или сколько процентов от этого уровня составит; 2. относительный показатель выполнения плана отражает фактический объем производства или реализации в процентах или коэффициентах по сравнению с плановым уровнем; 3. относительный показатель динамики отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом; 4. относительный показатель структуры - соотношение структурных частей изучаемого объекта и их целого; 5. относительный показатель координации отношение одной части совокупности к другой части этой же совокупности; 6. относительный показатель интенсивности - арактеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды; 7. относительный показатель сравнения - соотношение одноименных абсолютных показателей, характеризующих разные объекты. 42. Понятие средней величины. Значение метода средних величин. Средняя величина – обобщенная количественная характеристика признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Метод средних – это метод исследования статистической совокупности путем измерения ее средних величин (мер постоянства) Идея метода средних – вместо исходной совокупности рассматривают ее заменяющую совокупность, в которой все единицы одинаковы количественного группировочного признака). Этим достигается сопоставимость разных совокупностей (сравниваются не сами совокупности, а эти обобщающие показатели) 43. Виды средних величин и техника их вычисления. Вопрос полная херня, ничего непонятно Выделяются следующие основные виды средних величин: средняя арифметическая; средняя гармоническая; средняя квадратическая; средняя геометрическая. 1) варианты — это ряд числовых значений количественного признака (например, стаж, заработная плата, возраст). Варианты могут быть как абсолютными, так и относительными величинами; 2) частоты — это числа, показывающие, сколько раз повторяются соответствующие варианты (например, число рабочих). Частоты, как правило, обозначаются абсолютным числом Средняя арифметическая простая (невзвешенная) – вычисляется, когда каждый вариант совокупности встречается только один раз. Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле: 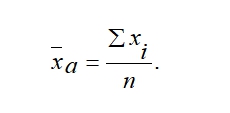 где хi – вариант, а n – количество единиц совокупности. где хi – вариант, а n – количество единиц совокупности.Средняя гармоническая применяется в тех случаях, когда требуется исчислить среднюю из величин, обратно пропорциональных изучаемому явлению, т.е. из относительных величин. Средняя гармоническая простая представлена ниже: 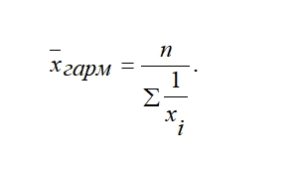 где xi – вариант, n – количество вариантов, где xi – вариант, n – количество вариантов,Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. Средняя геометрическая простая рассчитывается по формуле 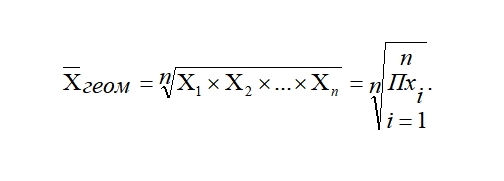 Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.Для несгруппированных данных используют формулу средней квадратической простой Средняя квадратическая простая 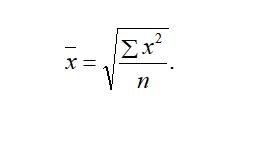 44. Понятие индексов и их значение. Виды индексов, используемых в уголовно-правовой статистике. Индекс – это показатель сравнений двух состояний одного и того же явления. Каждый индекс включает два вида данных: 1. оцениваемые данные, которые принято называть отчетными и обозначать значком «1»; 2. данные, которые используются в качестве базы сравнения, - базисные, обозначаются значком «0». Индекс чаще всего выражается как отношение, но может быть выражен в разностной форме, как разность между числителем и знаменателем отношения: Отношения = Отчетные данные: Базисные данные Индекс как отношение может быть выражен в виде: коэффициентов (когда базисный уровень принят за 1); процентов (когда базисный уровень принят за 100). Если индекс больше 1 (100%) – уровень изучаемого явления растёт. Если индекс меньше 1 (100%) – уровень изучаемого явления снижается. На практике индексный метод применяют для соизмерения сложных явлений, для выявления роли отдельных факторов в формировании какой-либо величины, для сравнения уровня явления не только с прошлым периодом, но и с другой территорией или нормативом.
Индивидуальный индекс – даёт сравнительную оценку отдельных элементов той или иной совокупности (или отдельной единицы совокупности). Общие (сводные) индексы – характеризуют изменение совокупности в целом по какому-либо признаку. Цепные индексы представляют собой сравнения текущих уровней с предшествующими или непрерывно меняющейся базой сравнения. Отношение базисного индекса к базисному индексу предшествующего периода: Базисные индексы имеют постоянную базу сравнения, в качестве которой принимаются данные какого-то одного периода (при анализе динамики), определенной территории (при территориальных сравнениях). 45. Понятие, виды и классификация рядов динамики. Ряд динамики - это ряд числовых значений статистического показателя расположенных в хронологической последовательности. Ряд динамики состоит из двух элементов (граф): 1. время (t) – это моменты (даты) или периоды (годы, кварталы, месяцы, сутки) времени, к которым относятся статистические показатели (уровни ряда). 2. уровень ряда (y) – значения статистического показателя, характеризующие состояние явления на указанный момент времени или за период времени. По времени: А) интервальные– ряды, уровни которых характеризуют размер явления за период времени (сутки, месяц, квартал, год). Б) моментные – ряды, уровни которых характеризуют размер явления на дату (момент) времени. По форме представления (способу выражения) уровней: А) ряды абсолютных величин. Б) ряды относительных величин. В) ряды средних величин. По расстоянию между датами или интервалам времени: А) полные (равные, равностоящие) – даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Б) неполные (неравные, неравностоящие) – даты регистрации или окончания периодов следуют друг за другом с неравными интервалами. По числу показателей: А) изолированные – во времени ведется анализ одного показателя. Б) комплексные – во времени ведется анализ системы показателей, связанных между собой единством процесса или явления. Для характеристики интенсивности изменения уровня ряда во времени такими показателями будут: 1) абсолютный прирост; 2) темпы роста; 3) темпы прироста. 46. Условия построения рядов динамики. При построении ряда динамики уровни ряда должны быть сопоставимы между собой: А) по территории, т.е. предполагаются одни и те же границы территории. Б) по кругу охватываемых объектов, т.е. предполагается сравнение совокупностей с равным числом элементов. В) по единицам измерения. Г) по времени регистрации. Д) по ценам. Е) по методологии расчета. 47. Характеристики ряда динамики. Для характеристики интенсивности изменения явления во времени рассчитываются показатели абсолютного прироста, коэффициента роста, темпа роста, темпа прироста, абсолютного значения одного процента прироста Коэффициент роста показывает, во сколько раз данный уровень превышает уровень, принятый за базу сравнения. Темп роста показывает, сколько процентов составляет данный уровень по сравнению с уровнем принятым за базу сравнения. Темп прироста показывает, на сколько процентов определенный уровень ряда больше (меньше) уровня, принятого за базу сравнения. Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах. для характеристики ряда динамики используют систему средних показателей динамики: средний уровень ряда; средний абсолютный прирост; средний темп роста; средний темп прироста. Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал (момент) из имеющейся временной последовательности. Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим в среднем за единицу времени. Средний темп роста показывает во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. 48. Сопоставимость уровней динамического ряда. Причины несопоставимости. Сопоставимость – это сравнимость показателей во времени. Основная причина несопоставимости рядов динамики заключается в том, что ряды динамики охватывают значительные периоды времени, за которые могут произойти изменения и привести к несопоставимости статистических данных. Несопоставимость данных во времени может быть вызвана следующими причинами: 1) территориальными изменениями; 2) изменением единиц счета; 3) изменением методологии расчетов; 4) изменением круга охвата объектов. 49. Методы приведения рядов динамики к сопоставимому виду. Методы приведение уровней рядов к сопоставимому виду: Метод смыкания рядов динамики – объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам (для осуществления смыкания необходимо, чтобы для одного из периодов, переходного, имелись данные, исчисляемые по разной методологии (или в разных границах)); Метод приведения рядов динамики к одному (общему или единому) основанию – приведение к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему (применяется, таким образом, для определения сравнительных характеристик направления и интенсивности роста одновременно развивающихся во времени явлений). Метод вычисления коэффициента опережения (замедления), то есть вычисление величины для сравнения базисных коэффициентов роста (или коэффициентов прироста) за изучаемый период 50. Тренд и методы выявления тренда в рядах динамики. Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия. Задача статистики – выявить общую тенденцию в изменении уровней ряда, освобождённую от действия различных случайных факторов. Изучение тренда включает два основных этапа: 1) ряд динамики проверяется на наличие тренда; 2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов. Методы выявления тренда (выравнивания, сглаживания ряда динамики): 1). Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупнённым интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т. е. укрупнить интервалы, то решение задачи упрощается. 2).Метод скользящей средней заключается в том, что исчисляется средний уровень из определенного числа (обычно нечётного) первых по счёту уровней ряда, затем – из такого же числа уровней, но начиная со второго по счёту, далее – начиная с третьего и т. д. Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобождённую от случайных или волнообразных колебаний. 3). Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов 51. Регрессионный анализ. Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. По сути, регрессионные методы показывают, как по изменениям «независимых переменных» можно зафиксировать изменение «зависимой переменной». Главной задачей регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием для выбора уравнения регрессии должен служить содержательный анализ природы изучаемой зависимости, её механизма. Помогает и графическое изображение корреляционного поля, задающего эмпирическую линию регрессии. Графически регрессия представляет собой теоретическую линию, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию корреляционной связи Требования к построению регрессионной модели: 1) совокупность исследуемых данных должна быть однородной и описываться непрерывными функциями; 2) все факторные признаки должны иметь количественное выражение; 3) объём исследуемой статистической совокупности должен быть достаточно большим; 4) должна прослеживаться причинно-следственная связь между изучаемыми явлениями или процессами; 5) территориальная и временная структура статистической совокупности должна быть постоянной. Этапы регрессионного анализа: 1) построение поля корреляции и выдвижение гипотезы о форме связи; 2) расчёт параметров предполагаемого уравнения регрессии; 3) интерпретация полученных результатов; 4) оценка статистической значимости уравнения регрессии. 52. Сезонные колебания в динамическом ряду. Сезонность- колебания показателя внутри года. Для годовых данных сезонность не определяется по сколько внутри она не вуалируется + и – отклонениями. Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (не менее трех) используют для того, чтобы выявить устойчивую сезонную волну, которая бы не отражала случайные условия одного года. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития. Индексы сезонности это процентные отношения фактических внутригодовых уровней к постоянной или переменной средней. При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период: Is=(yᵢ/yt)*100 В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев: Is=(yᵢ‾/ŷt)*100. 53. Понятие взаимосвязи явлений и процессов. Причинно-следственные отношения. Функциональная, статистическая и корреляционная виды связи. Причинно-следственные отношения - это связь явлений и процессов, при которой изменение одного из них - причины - ведет к изменению другого - следствия. Причина - это совокупность условий, обстоятельств, действие которых приводит к появлению следствия. Причинные связи носят всеобщий и многообразный характер, и для обнаружения причинно-следственных связей необходимо отбирать отдельные явления и изучать их изолированно. Особое значение при исследовании причинно-следственных связей имеет выявление временной последовательности: причина всегда должна предшествовать следствию, однако не каждое предшествующее событие следует считать причиной, а последующее - следствием. Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное (причем единственное!) значение другой. Например, между радиусом круга При статистическойзависимости изменение одной переменной приводит к изменению распределения другой. Например, статистической является связь между урожайностью и количеством внесенных удобрений, между ростом и весом человека и др. Корреляционная связь не является точной зависимостью одного признака от другого: она может иметь различную степень: от полной независимости до очень сильной связи. Кроме того, характер связи между разными признаками может быть различен по форме и направлению. 54. Основные приемы установления и измерения связи. 55. Коэффициент корреляции и его расчет. Коэффициент корреляции – это статистическая мера силы взаимосвязи между относительными движениями двух переменных. Диапазон значений от -1,0 до 1,0. Расчетное число больше 1,0 или меньше -1,0 означает, что при измерении корреляции произошла ошибка. Корреляция -1,0 показывает идеальную отрицательную корреляцию, а корреляция 1,0 показывает идеальную положительную корреляцию. Корреляция 0,0 показывает отсутствие линейной зависимости между движением двух переменных. Ключевые моменты Коэффициенты корреляции используются для измерения силы взаимосвязи между двумя переменными. Корреляция Пирсона – одна из наиболее часто используемых в статистике. Это измеряет силу и направление линейной зависимости между двумя переменными. Значения всегда находятся в диапазоне от -1 (сильная отрицательная связь) до +1 (сильная положительная связь). Значения, равные нулю или близкие к нему, означают слабую линейную зависимость или ее отсутствие. Значения коэффициента корреляции меньше +0,8 или больше -0,8 не считаются значимыми. Линейный коэффициент корреляции вычислим по формуле:  56. Статистический анализ, его цели, задачи и приемы. анализ статистических данных — это процесс изучения, сопоставления, сравнения полученных цифровых данных (между собой и с данными других отраслей социально-экономической статистики), их обобщения, истолкования и формулирования научных и практических выводов. Цели статистического анализа состоят в том, чтобы путём обработки, сравнения и сопоставления данных выяснить особенности изучаемых явлений, определить закономерности их развития и по результатам анализа сформулировать соответствующие выводы. Задачей анализа является раскрытие и изучение причин (факторов) изменения показателей, входящих в систему. Выявить все причины затруднительно и практически нецелесообразно Приемы статистического анализа: Прием сводки и группировки. Сводка предполагает подведение общего результата действия различных факторов на обобщающий показатель производственно-хозяйственной деятельности предприятия. Группировка заключается в выделении среди изучаемых явлений характерных групп по тем или иным признакам. Прием абсолютных и относительных величин. Абсолютные величины характеризуют размеры (величины, объемы) экономических явлений. Относительные величины отражают уровень выполнения плановых заданий, соблюдение норм, темпы роста и прироста, структуру, удельный вес или показатели интенсивности. Прием средних величин используется для обобщающей характеристики массовых, качественно однородных экономических явлений. Прием динамических рядов предполагает характеристику изменений показателей во времени, представление последовательных значений показателей, вскрытие закономерностей и тенденций развития. Прием сплошных и выборочных наблюдений. Сплошные наблюдения предполагают изучение всей совокупности явлений, характеризующих какую-либо одну сторону производственно-хозяйственной деятельности предприятия. Выборочные наблюдения имеют целью изучение хозяйственной деятельности предприятия на основе типовых представителей всей совокупности явлений или процессов. Прием детализации и обобщения. Детализация проводится путем разложения обобщающего (конечного) показателя на частные. Обобщения раскрывают связь между частями целого (объекта, явления, процесса), итогами деятельности отдельных подразделений и определяют степень их влияния на общее 57. Факторы, способствующие искажению криминологических показателей. 58. Правила статистических сравнений. Сущность сравнения – сопоставление однородных объектов с целью выявления сходства либо различий между ними. Технология сравнения: выбор сравниваемых объектов выбор вида сравнения выбор базы сравнения выбор числа показателей, по которым будут сравниваться объекты, выбор шкалы сравнения В экономическом анализе различают следующие виды сравнительного анализа: 1) горизонтальный - используется для определения абсолютных и относительных отклонений фактического уровня исследуемых показателей от базового; 2) вертикальный (структурный) -- используется для изучения структуры экономических явлений и процессов путем расчета: 3) трендовый -- используется для определения относительных темпов роста и прироста показателей за ряд лет по сравнению с уровнем базисного года; 4) одномерный -- сопоставления делаются по одному или нескольким показателям одного объекта или по одному показателю сопоставляются несколько объектов; 5) многомерный -- производится сопоставление результатов деятельности нескольких предприятий (объединений) по широкому спектру показателей для комплексной оценки хозяйственной деятельности 59. Определение типа сравнения данных: покомпонентное сравнение, позиционное сравнение, временное сравнение, частотное сравнение, корреляционное отношение. Выбор графика в зависимости от вида сравнения. Покомпонентное сравнение При покомпонентном сравнении мы прежде всего показываем размер каждого компонента в процентах от некоего целого. Увидев слова «доля», «проценты от целого», «составило Х%», вы можете быть уверены, что имеете дело с покомпонентным сравнением. 2. Позиционное сравнение При позиционном сравнении мы выявляем, как объекты соотносятся друг с другом: одинаковы ли они, больше или меньше других. (> Выручка клиента от продаж находится на четвертом месте.) Ключевыми словами для позиционного сравнения являются следующие: «больше чем», «меньше чем», «равно». 3. Временное сравнение В данном случае нас интересует не размер каждой доли в сравнении с целым, не соотношение долей, а то, как они изменяются во времени — что происходит с определенными показателями на протяжении недель, месяцев, кварталов, лет: возрастают ли они, снижаются, колеблются или остаются неизменными. (> Продажи в январе неуклонно росли.) Ключевые слова в данном случае: «изменяться», «расти», «убывать», «возрастать», «снижаться», «колебаться» и т. д. 4. Частотное сравнение Данный вид сравнения помогает определить, сколько объектов попадает в определенные последовательные области числовых значений. (> В мае сделки в основном заключались в диапазоне от одной до двух тысяч долларов.) Термины, характерные для этого вида сравнения, – «в диапазоне от х до у», «концентрация», «частотность» и «распределение». 5. Корреляционное сравнение Корреляционное сравнение показывает наличие (или отсутствие) зависимости между двумя переменными. Например, обычно ожидается, что при увеличении объемов продаж возрастает прибыль или что при увеличении скидок возрастают объемы продаж. Если формулировка вашей идеи содержит такие слова, как «относится к», «возрастает при (в случае)», «снижается при (в случае)», «меняется при (в случае)» или, наоборот, «не возрастает при (в случае)» и т. д., это указывает на применение корреляционного сравнения. Любая сформулированная вами идея всегда может быть выражена с помощью одного из пяти типов сравнения. Каждому из этих типов сравнения соответствует один из пяти основных типов диаграмм: круговая, линейчатая, точечная диаграммы, гистограмма или график. 60. Понятие, основные задачи и правила обобщения (синтеза) статистических данных о социально-правовых явлениях. Статистическое обобщение — это умозаключение неполной индукции, в котором установленная в посылках количественная информация о частоте определенного признака в исследуемой группе (образце) переносится в заключении на все множество явлений этого рода. Задачи: выделение в совокупности изучаемых явлений их социально-экономических типов; изучение структуры общественных явлений; выявление связей и зависимостей между общественными явлениями | |||||||||||||||
