1. Сущность проблемы автоматического управления. Принципы и алгоритмы управления. Примеры систем автоматич. Управления(сау). Основные понятия и определения
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
1. Сущность проблемы автоматического управления. Принципы и алгоритмы управления. Примеры систем автоматич. Управления(сау). Основные понятия и определения. Управление – такая организация того или иного процесса, который обеспечивает достижение определенных целей.Автоматическое управление – управление осуществляемое без участия человека. Автоматизированное управление- управление с участием человека. Этапы процесса управления:1.Сбор и обработка информации о положении объекта в целях оценки сложившейся ситуации. 2. Принятие решения о целесообразности действий 3. Исполнение принятого решения. ОУ – объект управления. Фактическое состояние ОУ определяется 1 или несколькими рабочими параметрами:  - физ. величины: t,v,u и т.д. - физ. величины: t,v,u и т.д.В реальных условиях на ОУ оказывают влияние внешние воздействия – возмущающие z(t). Они вызывают отклонение (изменение) внутреннего состояния ОУ и, как следствие, рабочих параметров. В связи с этим, для выполнения работы по заданным алгоритмам, необходимо на ОУ организовывать подачу управляющих воздействий U(t). Если это представить в виде схемы: Заданный алгоритм обычно предусматривает поддержание раб параметра постоянным во времени или изменение по известному или неизвестному знаку.  Задача управления заключается в формировании такого закона изменения управления воздействия, при котором обеспечивает заданный алгоритм при наличии возмущающего воздействия. Для решения задач используются 3 фундаментальных принципа управления: 1.Разомкнутое управление 2.Управление по возмущению 3.Замкнутое управление (принцип обратной связи) Схематично эти принципы выглядят так: , где УУ управляющие устройства; И –измеритель возмущения, К – корректирующее устройство. 
УУ в зависимости от величины и знака ошибки вырабатывает сигнал V, т.о. принцип замкнутого управления учитывает не только задание, но и фактическое значение параметра ОУ и действующих возмущений. Наиболее универсальный метод. Класс автоматических систем, построенных на основе 3-го принципа получил название систем автоматического регулирования (САР). 2. Виды задающих и возмущающих воздействий. Методика расчета характеристик линейных стационарных Сау. Они представляют собой непрерывные функции времени с различными значениями изменения. В качестве типовых используют воздействия полиномиального вида:  , где n=0,1,2… ; fn – постоянные величины; 1(t) – единичная ступенчатая функция. 1(t) = 0, при t<0 и 1(t)=1, при t>=0. , где n=0,1,2… ; fn – постоянные величины; 1(t) – единичная ступенчатая функция. 1(t) = 0, при t<0 и 1(t)=1, при t>=0.При n=0 полиномиальное выражение определяет ступенчатое воздействие:  При n=1 получим меньшее значение с постоянной скоростью:   При n=2 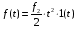 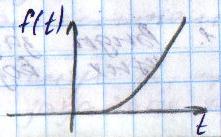 Единичная дельта функция (единичный импульс) – представляет собой математическую идеализацию импульса бесконечно малой длительности и бесконечно большой амплитуды и имеющего конечную площадь равную 1.  Связь между 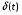 и 1(t): и 1(t): 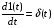 Гармонически типовые воздействия:  , где , где k-const,  - частота, - частота,  - фаза. - фаза. 3. Математическое описание САУ. Основы теории преобразования Лапласа. Поведение САУ в процессе функционирования представляет собой сочетание статистических и динамических режимов. Для проведения теоритических исследований необходимо иметь уравнение, описывающее поведение отдельных элементов при изменяющихся внешних воздействиях. Эти выражения в математической форме – соотношение, связывающее входной и выходной сигналы и воздействия. С целью упрощения математического отношения вводим допущение:
Рисунок 1 САУ - обобщенный вид. Действие непрерывной линейной САУ описывается (не)?однородным дифференциальным уравнением:  (1) (1)А, б, С – постоянные координаты, зависящие от параметров системы 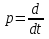 - Оператор дифференцирования - Оператор дифференцирования Операторный вид дифференциального уравнения  ( ( )x= )x= (2) (2) - полином при y - Собственный оператор Q(t) - полином при y - Собственный оператор Q(t) - полином при x - Оператор управляющего воздействия R1(p) - полином при x - Оператор управляющего воздействия R1(p) - полином при z - Оператор возмущающего воздействия R2(p) - полином при z - Оператор возмущающего воздействия R2(p) (3) (3)Если рассмотрим только установившийся режим, то 2 принимает вид:  (4) (4)Уравнение 2 описывает как динамику так и статику САУ, а 4 – только статику. Операторный вид дифф/ уравнение 2го порядка:  (5) (5) (6) (6) - Постоянные времени; - Постоянные времени; 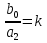 – (безразмерный коэффициент) – (безразмерный коэффициент) Q(p)- Принимает вид алгебраического уравнения:  (Оператор Р – оператор преобразования Лапласа.) Для линейных дифференциальных уравнений с постоянными параметрами при нулевых начальных условиях с точностью до обозначения оператор P соответствует оператору S: P≡S. Это обстоятельство позволяет использовать для решения 1 интегральное преобразование Лапласа: (Отображение функции f(t): )  ; ;  f(t)- оригинал; f(s) - изображение f(t)- оригинал; f(s) - изображениеОбратное преобразование Лапласа: 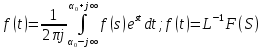 4. Передаточные функции. Передаточная функция (ПФ) является моделью САР, т.к. полностью характеризует динамические свойства системы. ПФ – представляет собой отношение изображения по выходной величине Y(S) к изображению входной величине Х(S).  Учитывая  , можно для линейной системы записать уравнение в вида: , можно для линейной системы записать уравнение в вида:Q(S)*Y(S)= R1(S)*X(S)+R2(S)*Z(S) Поскольку для линейной системы можно применить принцип наложения, то будет справедливо выделить 2 случая:
Q(S)*Y(S)=R1(S)*X(S)
Q(S)*Y(S)=R2(S)*Z(S) Тогда для любой САР, имеющей входы по управлению и возмущению можно записать: ПФ по управлению: 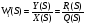 ПФ по возмущению: 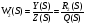 Так как    Тогда  ; ;  Для физической реализации системы необходимо, чтобы выполнялось условие: n>m; n>k. 5. Структурные схемы линейных Сау и их преобразования. Система состоит из элементов которые соединяются последовательно, параллельно или с помощью обратной связи. Каждый элемент имеет 1 вход и 1 выход и заданную ПФ. Есть правила, которые позволяют по отдельным ПФ элементов получить ПФ всей системы.
1) 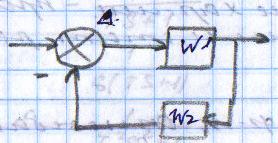 обратная связь может быть “–“ обратная связь может быть “–“ 2) Если обратная связь “+“, то   Пусть нам задана в общем виде структура САР:  По управлению: 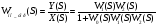 По возмущению:  По ошибке:  6. Системные характеристики САУ (временная, переходная, импульсная). Временные характеристики САУ:
Графическое представление этих функций называется временными характеристиками, процессы, проходящие в динамических и статических режимах. Переходной функцией H(t) – называется функция описывающая сигнал на выходе, при условии, что на вход подана единичное ступенчатое воздействие при нулевых начальных условиях. График H(t) называется переходной характеристикой. Весовой (импульсной) функцией W(t) называют функцию описывающую реакцию на единичное импульсное воздействие при нулевых начальных условиях. График называется импульсной характеристикой. Аналитическое определение переходных функций и характеристик основано на следующих положениях:
Где Т- постоянная времени. Так как изображение единичного ступенчатого воздействия равно 1/S, то изображение переходной функции определяется соотношением:  . .Для нахождения переходной функции необходимо передаточную функцию разделить на S и выполнить преобразование Лапласа(переход от изображения к оригиналу). (изображение единичного импульса =1, тогда)Изображение импульсной функции:  . ( переходная ф. явл. Изображением импульсной ф.) . ( переходная ф. явл. Изображением импульсной ф.) ; ; 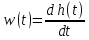 Две рассмотренные характеристики являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях. 7. Системный характеристики Сау(частотная, передаточная) Частотные характеристики (ЧХ) могут быть получены экспериментально и аналитически. Если задана ПФ W(S), то путем подстановки  получаем частотную ПФ получаем частотную ПФ  которая является комплексным выражением состоящим из действительной части которая является комплексным выражением состоящим из действительной части  и мнимой и мнимой  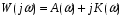 Показательная форма частотной ПФ (ЧПФ):    Функция 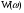 , представленная при изменении частоты от нуля до бесконечности получила название АЧХ. , представленная при изменении частоты от нуля до бесконечности получила название АЧХ.Функция  , полученная таким же образом, называется ФЧХ. , полученная таким же образом, называется ФЧХ.ЧПФ  можно представить на комплексной плоскости, в этом случае для каждой из частот в диапазоне от нуля до бесконечности производится определение вектора на комплексной плоскости и строится годограф вектора. Годограф будет представлять собой АФЧХ. можно представить на комплексной плоскости, в этом случае для каждой из частот в диапазоне от нуля до бесконечности производится определение вектора на комплексной плоскости и строится годограф вектора. Годограф будет представлять собой АФЧХ. Для определенной частоты имеем вектор на комплексной плоскости который характеризуется модулем и аргументом. Модуль – отношение амплитуды выходного гармонического сигнала к амплитуде входного. Аргумент – сдвиг по фазе выходного сигнала по отношению к входному. При этом “–” фазовый сдвиг отображается вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси и наоборот. Для упрощения графического представления ЧХ используются логарифмические ЧХ: ЛАЧХ и ЛФЧХ. На шкале частот вместо  откладывают lg( откладывают lg( ) и единицой измерения является декада – интервал частот, соответствующий изменению частоты в 10 раз. ) и единицой измерения является декада – интервал частот, соответствующий изменению частоты в 10 раз.На оси ординат при построении ЛАЧХ единицей измерения является децибел. 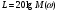 8. Типовые динамические звенья. Типовые звенья – составная часть системы, в которая описывается дифференциальным уравнением не выше 2-го порядка. Делятся на: позиционные(П), дифференцирующие(Д), интегральные(И) П – такие, у которых в установившемся режиме наблюдается линейная зависимость между входными и выходными сигналами. Д – такие, у которых выходной сигнал пропорционален производной по времени от входного сигнала. И – такие, у которых выходной сигнал пропорционален интегралу входного сигнала. Звено считается заданным, если известна его ПФ или дифференциальное уравнение. Звенья имеют временные и частотные характеристики. ПФ любой САР можно представить как произведение передаточных функций. Виды звеньев:
|

 - ошибка, отклонение; которая является разностью между заданным и фактическим значением параметра:
- ошибка, отклонение; которая является разностью между заданным и фактическим значением параметра: 
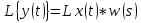 . Изображение выходного сигнала – это произведение изображения входного сигнала на переходную функцию. Сигнал y(t) можно получить как обратное преобразование Лапласа для простых звеньев.
. Изображение выходного сигнала – это произведение изображения входного сигнала на переходную функцию. Сигнал y(t) можно получить как обратное преобразование Лапласа для простых звеньев. 
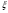 <
< )
) , где
, где  - время запаздывания.
- время запаздывания.