1. Сущность проблемы автоматического управления. Принципы и алгоритмы управления. Примеры систем автоматич. Управления(сау). Основные понятия и определения
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
9) Понятие устойчивости. Постановка задачи устойчивости. Устойчивость – важнейшая качественная характеристика динамических свойств САУ. Устойчивость САУ связана с поведением системы после прекращения внешнего воздействия. Устойчивость системы – затухание ее переходных процессов. Если система представлена в виде переходной функции, то для анализа устойчивости используется знаменатель переходной функции, ее собственный оператор. 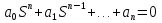 (1) n – порядок полинома (1) n – порядок полиномаКорни характеристического уравнения можно разместить на комплексной плоскости. Для устойчивой системы необходимым и достаточным условием является: Все корни должны находится слева от (мнимой) оси. Если хотя бы один корень или пара комплексно сопряженных находится справа, то система неустойчива. Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной, находится на границе устойчивости и не устойчивости. Мнимая ось – граница устойчивости. С целью Упрощения анализа разработан ряд (математических) критериев устойчивости: Алгебраический (Аналитические характеристики); Частотный(Графо-аналитические хар.). 10. Алгебраические критерии устойчивости линейных САУ. Алгебраический критерий устойчивости Гурвица. Матрица Гурвица:  По диагонали матрицы от верхнего левого угла записываются все коэффициенты начиная с a1. Затем каждый столбец дополняется таким образом, чтобы вверх от диагонали индексы при коэффициентах увеличивались, а вниз – уменьшались. Все остальные позиции заполняются нулями. Для устойчивой системы необходимым и достаточным является то, чтобы при a0>0 все диагональные определители были также положительными, т.е. 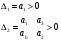 и т.д. и т.д.Система будет нейтральной, если все определители положительны, а последний равен нулю. 11. Частотные критерии устойчивых линейных САУ. Частотный критерий Михайлова предполагает построение годографа на комплексной плоскости.    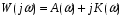 АФЧХ – при сканировании частоты от нуля до бесконечности. Аналитическое представление вектора: 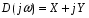 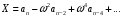 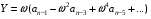 Построение годографа производится по уровню вектора 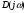 при изменении от 0 до бесконечности. Для устойчивой системы n-го порядка необходимо и достаточно, чтобы при при изменении от 0 до бесконечности. Для устойчивой системы n-го порядка необходимо и достаточно, чтобы при 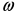 =0 годограф начинался на вещественной положительной оси и проходил против часовой стрелки n квадрантов, нигде не обращаясь в 0. Если годограф начался в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной, т.е. находится на границе устойчивости и неустойчивости. =0 годограф начинался на вещественной положительной оси и проходил против часовой стрелки n квадрантов, нигде не обращаясь в 0. Если годограф начался в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной, т.е. находится на границе устойчивости и неустойчивости.12) Оценка качества регулирования. Коррекция САУ. Оценки качества могут быть прямыми и косвенные, и те и другие могут быть статическими(установившийся) и динамическими(переходный процесс). (Прямые оценки качества - определяются по переходной характеристике, каналу управления, возмущения) Если характеристика представляет собой затухающие колебания, то система устойчива.( При этом допускается не более двух колебаний. )К прямым относятся: 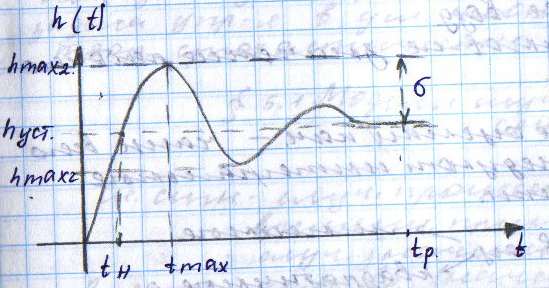 σ- Перерегулирования tp- Время регулирований w- Чaстота колебаний n- Число колебаний за время tn- Время нарастания переходного процесса tmax- Время достижения первого максимума tp- Характеризует длительность переходного процесса. 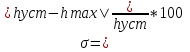 : : 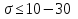 Переходная характеристика не должна выходить за область допустимых отклонений. В статическом режиме САУ оценивается коэффициентом статизма или астатизма. 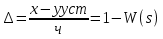 Yуст- Установившиеся значения рабочего параметра; Х- Задающее воздействие Косвенные оценки качества. Наиболее распространены интегральные: линейные, квадратичные. Численно – интегральная оценка равна площади ограниченной кривой ошибке или разности (х-у). 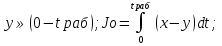 Может применяться при монотонных переходных процессах, при отсутствии коллебаний. Может применяться при монотонных переходных процессах, при отсутствии коллебаний. Квадратичная интегральная оценка применяется как при монотонных так и при колебательных процессах. 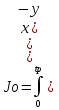 Коррекция САУ.В этом случае если необходимые параметры качества не могут быть достигнуты, то применяется коррекция. Корректирующие элементы могут быть включены различными способами: 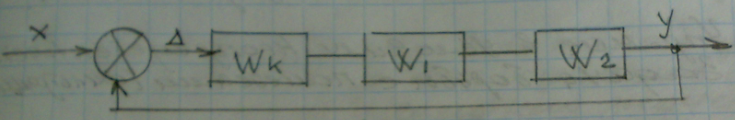 Если корректирующие устройства вводят производную, то происходит повышение качества переходного процесса. 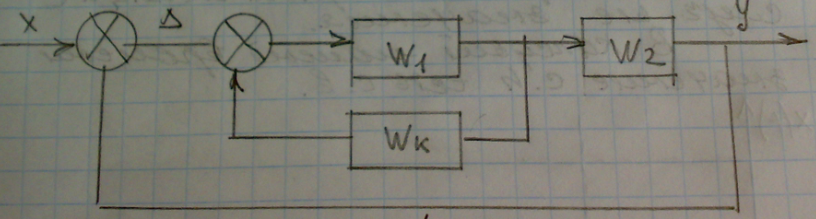 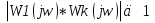 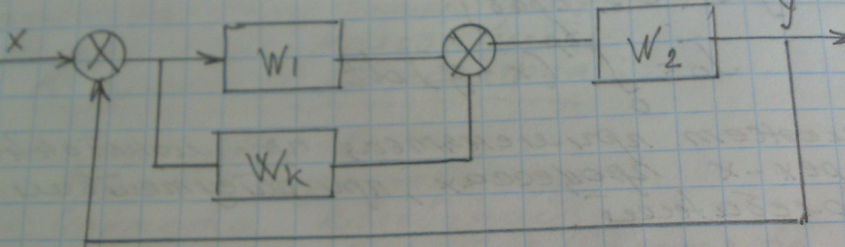 13. Основы теории случайных процессов. Корреляционный и спектральный анализ. Примеры расчета. Случайные процессы (СП) В реальных системах имеются помехи, действующие в каналах передачи информации, к этому добавляются неточные значения параметров САУ, часто не имеется никакой, кроме статистической информации об этих процессах – это заставляет считать эти параметры случайными величинами, так возникают задачи управления в условиях неопределенности, т.е. теория стохастических САУ. Случайные сигналы – случайные процессы, т.е. функции времени принимающие случайные значения.В каждый момент времени значение случайного процесса есть случайная величина. 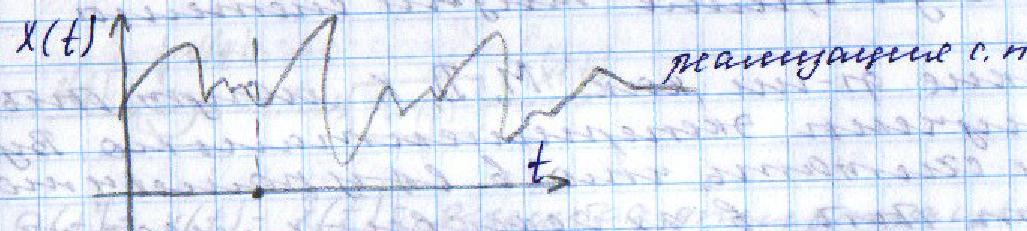 P(x,t) – плотность вероятности в момент t. 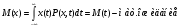 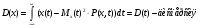 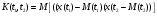 - корреляционная функция, показывающая корреляцию процесса в 2 разных момента времени. - корреляционная функция, показывающая корреляцию процесса в 2 разных момента времени.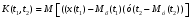 - взаимная корреляционная функция сигналов х и у. - взаимная корреляционная функция сигналов х и у.Корреляционная функция описывает связь значений процессов в разный момент времени. Стационарный – такой СП, для которого корреляционная функция зависит не от значений t1 и t2, а только от их разностей. 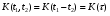 . Для стационарных СП мат.ожидание и дисперсия могут быть получены экспериментально. Будем считать, что в САУ помехи могут быть в 2х основных местах – в канале управления и измерителе. . Для стационарных СП мат.ожидание и дисперсия могут быть получены экспериментально. Будем считать, что в САУ помехи могут быть в 2х основных местах – в канале управления и измерителе.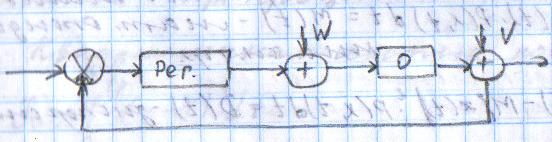 W – помеха в канале управления.V – помеха в измерителе.О – объект управления. Спектральная плотность стационарных СП: 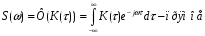 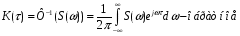 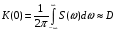 Взаимная спектральная плотность 2х процессов x и y: 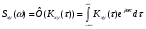 Задача фильтрации позволяет построить фильтрацию которая max убирает помехи. Полезный сигнал – также случайный сигнал с известной случайной плотностью. 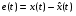 - ошибка фиильтрации - ошибка фиильтрации Необходимо определить W(p), чтобы 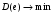 при известных x(t) и v(t). при известных x(t) и v(t).14. Нелинейные САУ. Типовые нелинейные звенья. С т.зр. мат описания САУ делятся на линейные и нелинейные. Нелинейные САУ – сис-мы содержащие хотя бы 1 нелинейный элемент (звено), к-ый описывается нелинейным ур-нием.
15) Стационарные режимы нелинейных систем при случайных воздействиях. Cтатистическая линеаризация. В случае нелинейных систем не применим принцип супер позиции. Специально создан метод статистической линеаризации, который заключается в замене нелинейной системы – линейной – эквивалентной исходной системе в отношении реакции на заданное случайное воздействие. Идея статистической линеаризации: рассмотрим не линейное звено с характеристикой: 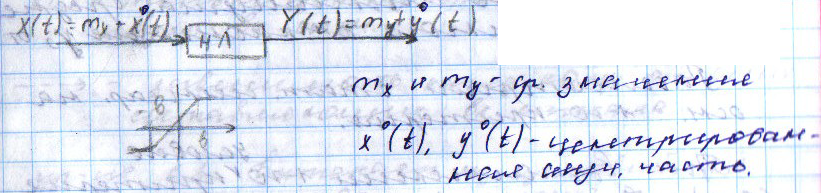 Hа входе и выходе: стационарный случайный сигнал. Задача статистической линеаризации состоит в том, чтобы найти линейное звено, дающее при том же входном сигнале х(t), выходной сигнал У эквивалентный от t: 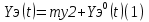 с достаточной точностью приближающейся к сигналу y(t) на выходе нелинейного звена: Yэ(t)≈Y(t). Точность линеаризации зависит от критерия выбранного для сравнения. с достаточной точностью приближающейся к сигналу y(t) на выходе нелинейного звена: Yэ(t)≈Y(t). Точность линеаризации зависит от критерия выбранного для сравнения.Критерии:
Статистическая линеаризация на основе первого критерия. При выполнении первого условия уравнения 2 линейное звено будет полностью эквивалентно не линейному в отношении пропускания заданной детерминированной составляющей входного сигнала. Второе условие 2 является условием эквивалентности в отношении пропускания центрированной случайной составляющей, в этом случае не линейное звено может быть заменено линейным эквивалентом, которое описывается уравнением: 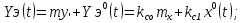 идеальным статистическим звеном с разными коэффициентами передачи, для детерминированной ( идеальным статистическим звеном с разными коэффициентами передачи, для детерминированной (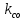 ) и случайной ( ) и случайной (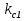 ) составляющей сигнала. ) составляющей сигнала. Эквивалентно линейное звено полученное при статистической линеаризации. 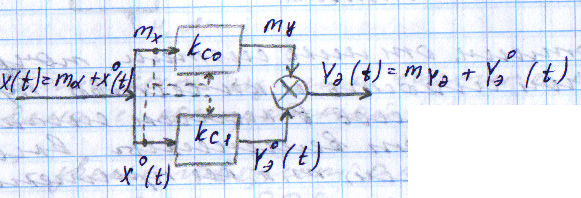 Штрих – стрелками показано условная зависимость каждого коэффициента от обеих составляющих входного сигнала. 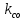 - пропускает ср.знач, а звено - пропускает ср.знач, а звено 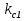 – только центрированную составляющую вх.сигнала. – только центрированную составляющую вх.сигнала.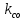 =my/mx; =my/mx; 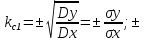 - определяется возрастанием или убыванием линеаризуемой функции. Коэффициенты статистической линеаризации – - определяется возрастанием или убыванием линеаризуемой функции. Коэффициенты статистической линеаризации –16. Особенности динамики нелинейных систем. Гармоническая линеаризация. Из-за отсутствия принципа суперпозиции в нелинейных системах после прекращения воздействия вх сигнала возникают собственные колебания. Такие устойчивые собственные колебания с постоянной амплитудой определяемой нелинейностями системы наз автоколебаниями. 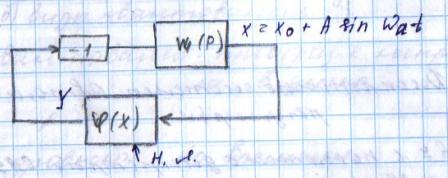 Система состоит из линейной части Wл и нелинейного звена φ(x). Полагаем,что в системе есть автоколебания, амплитуду и частоту которых хотим найти. Х,У – периодические функции времени. Метод основан на предположении, что колебания на входе НЛ звена явл синусоидальными. А – амплитуда, wa - частота автоколебаний, х0 – постоянная составляющая. Идея: в замене НЛ звена эквивалентным линейным, это линейное звено состоит из 2х параллельных подзвеньев, одно из к-ых пропускает постоянную составляющую, а другое только синусоидальную составляющую автоколебаний. 17. Понятие о дискретных системах. Классификация. В САУ непрерывного действия все сигналы непрерывны во времени. В дискретных САУ хотя бы 1 величина представляет собой дискретный сигнал, к-ый изменяется дискретно, скачками. 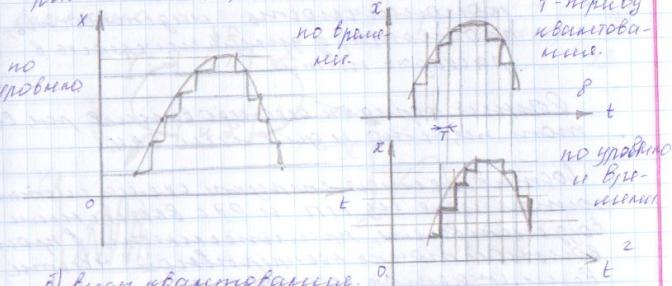 Дискретные системы: чисто дискретные (только диск-е сигналы), смешанные В соответствии с видами дискретных сигналов: релейные, импульсные, цифровые. 18) Релейные САУ. Осуществляется квантование сигнала по уровню напрерывного сигнала Х в дискретный У. НП – непрерывная часть. F – внешнее воздействие. Ре – Релейный элемент, который осуществляет квантование сигнала х по уровню в дискретный сигнал у. 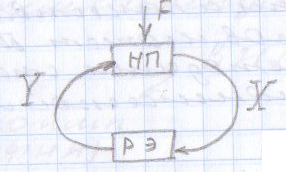 Основное достоинство: простота, надежность, экономичность. Общий порядок исследования, как и для линейных САУ : (математическое описание, исследование устойчивости, характеристики переходного процесса,) составляется структурная схема системы состоящая из НП и РЭ с внешним воздействием F, приложенным в произвольной точке непрерывной части. Если участок от места приложения внешнего воздействия, непрерывной части до релейного элемента – линейный, то воздействие может быть перенесено на вход РЭ. 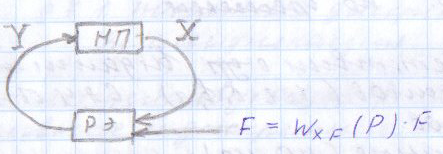 Исследование устойчивости и качество релейной САУ можно осуществлять на базе методов гармонической и статистической линеаризации. 19. Импульсные САУ. Системы в которых действуют сигналы квантованные по времени. Большинство САУ можно представить следующим рисунком: 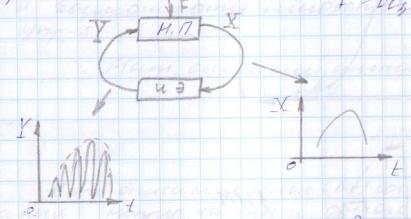 Преобразование непрерывного сигнала Х в дискретный У – импульсная модуляция, заключается в изменении одного из параметров вых импульсов в функции величины вх сигнала. Импульсные модуляции: 1. Амплитудо-импульсная (АИМ) 2. Широтно-имп-я (ШИМ) 3. Время-имп-я (ВИМ): частотно-имп-я, фазо-имп-я Мат. Описание Состоит из описания НП и ИЭ, для описания ИЭ необходимо знать форму вых импульса, статическую хар-ку элемента и его время запаздывания, если оно существенно. Статич-я хар-ка – зависимость модулируемого параметра от вх модулирующего сигнала. Вып-ся 3 преобразования структ-й схемы САУ: 1. Разлагаем реальный ИЭ на идеальный и формирующий элементы 2. Переносим внешнее воздействие на вход ИЭ 3. Заменяем в действующей системе реальные непрерывные сигналы на фиктивные дискретные. 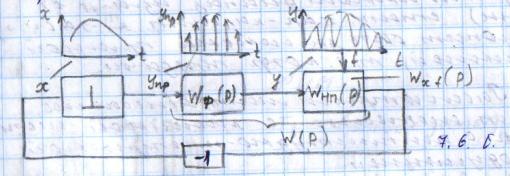 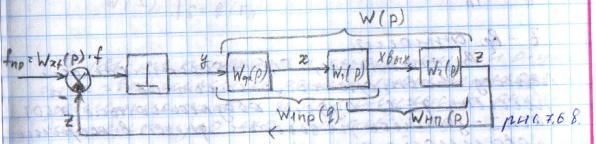 Реальный ИЭ представляется в виде последовательного соединения идеального ИЭ и формирующего элемента. Сигнал на вых формирователя наз идеальной импульсной функцией. Перенос внешнего воздействия на вход ИЭ осуществляется обычным пересчётом через передаточную ф-цию.В результате 3-го преобразования мы получаем сис-му в к-ой сущ-ют только дискретные переменные, при этом мы переходим от обычных диф уравнений к разностным Ур-ниям и соответственно от обычного преобразования Лапласа к дискретному. Непрерывная ф-ция x(t) ИЭ заменяется на дискретную ф-цию значения к-ой в начале каждого периода, те в моменты nTn, где n=1,2… совпадают со значенияминепрерывной функции, а в остальное время =0, такая дискретная ф-ция решётчатая (x[nTn]). Непрерывная функция x(t) огибающая для дискретной функции.Переход к изображению Лапласа сводится к нахождению по оригиналу внешнего воздействия его изображения и замене в передаточной функции оператора дифференцирования р на комплексную переменную S, переход далее к относительному времени заключается в замене S→q/Tn, где q – комплексная переменная в относительном времени. Разделить это изображение Fпр(S) на Tn, при S=q/Tn;Fпр(S)*1/ Tn| S=q/Tn x(at)=1/a*x(-S/a) 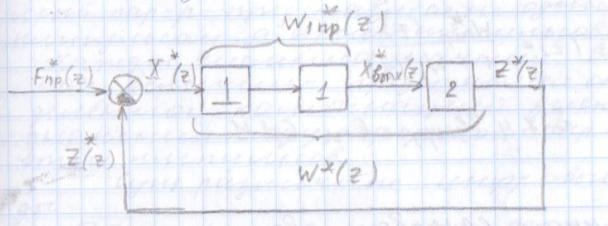 Соответственно осущ-ся переход к относительному времени для передаточной функции W(S)| S=q/Tn |