1. Сущность проблемы автоматического управления. Принципы и алгоритмы управления. Примеры систем автоматич. Управления(сау). Основные понятия и определения
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
20, Цифровые САУ В цифровых САУ квантование и по уровню и по времени. Это системы в которых существуют дискретные сигналы в виде цифрового кода. В качестве преимущества в цифровых САУ отличаются наиболее совершенными алгоритмическими возможностями. Характерная особенность: в состав управляющего устройства входит ЦВМ. Тогда схема САУ будет выглядеть так: 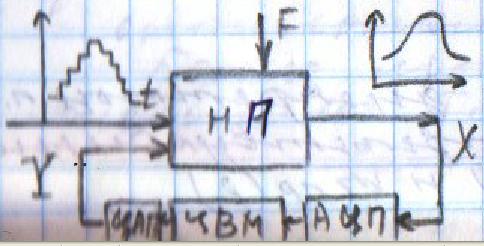 Цифровая САУ Цифровая САУМП – непрерывная часть САУ, объект управления. 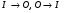 - преобразование непрерывной величины в цифровую и наоборот. - преобразование непрерывной величины в цифровую и наоборот.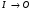 - кодирование - кодирование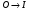 - декодирование. - декодирование.В отличие от импульсных САУ, модулируемый параметр представляется не одним импульсом, а серией импульсов. Каждое численное значение входной величины представляется определенной комбинацией дискретных значений модулируемого параметра этих импульсов. Существуют различные цифровые коды. Простейший из них – единичный код. Каждое значение дискретной величины = числу импульсов. Наибольшее распространение получил двоичный код. Модулируемому параметру каждого импульса, представляющего значение одного из разрядов передается одно из 2х крайних значений. Знак передается с помощью отдельного импульса с двумя возможными значениями. Преобразование 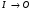 содержит погрешность из-за квантования по уровню, т.е. округление численного значения до целого числа, соответствует уровню квантования. Абсолютное значение погрешности квантования определяется длиной шага квантования. содержит погрешность из-за квантования по уровню, т.е. округление численного значения до целого числа, соответствует уровню квантования. Абсолютное значение погрешности квантования определяется длиной шага квантования.Во всех цифровых САУ преобразование 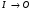 осуществляется путем квантования численного значения до ближайшего уровня. осуществляется путем квантования численного значения до ближайшего уровня.Дает: высокую точность(определяется числом разрядов цифрового кода), помехозащищенность(Ц САУ > чем у импульсных из-за кодов представления информации, она практически не ограничена за счет введения избыточности), возможность реализовывать сложные алгоритмы. Основная область применения: где требуются системы со сложными алгоритмами – САУ самолетами и т.д. При уменьшении шага квантования, т.е. при увеличении числа уровней квантования цифровых систем приближается по свойствам к импульсным. Особенностью динамики Ц САУ по сравнению с импульсными является наличие фиксированного временного запаздывания в управляющем устройстве – это длительность 1го цикла обработки информации в ЦВМ. Мат описание цифрового САУ. Математическое описание осуществляется как для импульсных САУ с помехами разностных уравнений и дискретного преобразования Лапласа путем замены, действующих в МП части системы непрерывной величин фективными дискретными в виде решетчатых функций. Однако, в связи с тем, что имеется ещё и квантование по уровню, структурная схема Ц САУ содержит помимо импульсных элементов нелинейные звенья – квантователи, описываемые многоступенчатой релейной статической характеристикой. Структурная схема 1 Ц САУ: 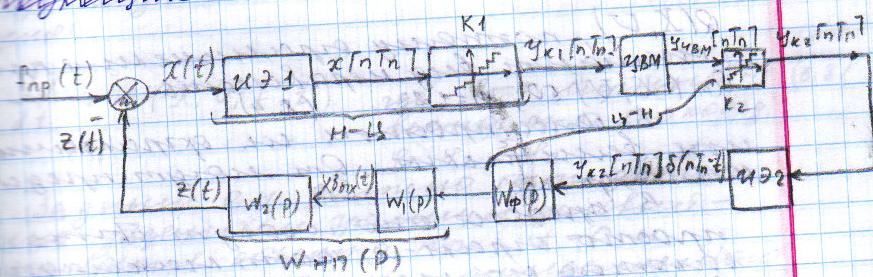 Преобразователь 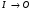 представлен последовательным соединением ИЭ1 и квантователя К1 представлен последовательным соединением ИЭ1 и квантователя К1ИЭ1 – квантов, по времени осуществляет преобразуя входную функцию x(t) в последовательность её дискретных значений через период квантования Tn, т.е. в решетчатую функцию. К1 – осуществляет квантование по уровню Структурная схема 2 Ц САУ: 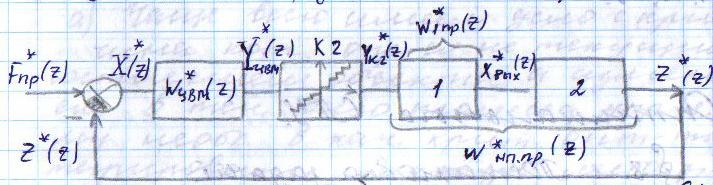 Квантование не учитывается Переменные записаны решетчатыми функциями Выходная величина (X*вых(z)) показана в общем случае в промежуточной точке непрерывнолй части системы. Внешнее воздействие F*пр(z) приведено ко входу ЦВМ. Дискретная ПФ W*цвм(z) описывает ЦВМ со входным импульсом ИЭ1. Дискретная ПФ W*пр(z) описывает участки системы от входа ИЭ2(схема 1) соответственно до места нахождения выходной величины X*вых(z) и до выхода z*(z) непрерывной части системы. Если выберем малый шаг квантования, то можно принебречь K2 и тогда получим предельную импульсную систему:  21. Оптимальные Сау. Постановка задачи, критерии оптимальности, обзор методов решения. Оптимальные САУ – система в которой обеспечено оптимальное значение какого-либо основного показателя качественной работы системы. Оптимальные показатели качества – критерии оптимальности (эффективности целевой функции). Для САУ критерием оптимальности могут быть: показатели качества переходных процессов (длительность, точность, время перерегулирования). Задача синтеза оптимальных САУ: глобальная проблема: есть несколько показателей которые противоречивы. Обычно обеспечивают оптимальность одного из показателей качества системы при учете требований к остальным показателям в виде ограничений на их значения. Чтобы корректно составить задачу синтеза оптимальных САУ остановимся на математическом описании: а) критерии оптимальности, б) ограничения, в) объекты управления. А) Чаще всего имеет дело с критерием величина которого определяется не текущим состоянием объекта, а изменением его в течении всего процесса управления. Поэтому необходимо в качестве критерия оптимальности интегрировать какую-либо функцию величина которой зависит от текущего состояния объекта. Функция выхода величины объекта Х и управляющего воздействия V которые являются векторами содержащими произвольное число составляющих. – длительность процесса управления. Обычно Q составляется так, чтобы его значение стремилось к минимуму. Функционалы: 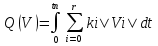 - Применяются при минимизации расходов рабочего тела (топлива) и это определяется величиной управляющего этим расходом воздействием I. Такая задача характерна для систем управления полетами. - Применяются при минимизации расходов рабочего тела (топлива) и это определяется величиной управляющего этим расходом воздействием I. Такая задача характерна для систем управления полетами.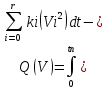 Применимо в задачах на мин. Энергии, когда величина квадрата управляющего воздействия определяет мощность расходуемую при управлении объектом. Применимо в задачах на мин. Энергии, когда величина квадрата управляющего воздействия определяет мощность расходуемую при управлении объектом.ki- Коэффициент пропорциональности Общими математическим аппаратом является вариационное исчисление (метод динамического программирование Р.Беллмана, принцип максимуму Л.С.Понтрягина) 22. Принцип максимума Л.С.Понтрягина 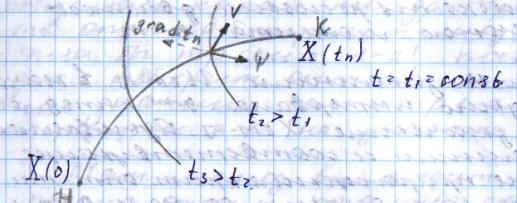 Пусть стоит задача о переводе за минимальное время изображающей точки из положения Н в положение К. Вокруг конечной точки можно построить поверхности являющиеся геометрическим местом точек с одинаковым минимальным временем ti перехода в эту точку, такие поверхности называются изокронами. Очевидно, что оптимизированная по быстродействию траектория из т.Н в т.К должна быть макс-но близка нормалям к изокронам. Математически это условие оптим-ной траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости V=dx/dt на вектор обратный градиенту времени перехода в точку К должно быть макс-но. Если обозначить это произведение через Н, а вектор обратный градиенту времени перехода ψ=-grad tn, то H= ψV=Σ(i=1 n) ψiVi=max ψi и Vi – координаты векторов Многовекторность фазового пространства Каждой точке фазового пространства окружающего т.К соответствует определённая оптимальная траектория и отвечающее ей миним-е время перехода в эту точку. Условием мксим-ти явл-ся максим-м проекции вектора V на направление ψ 23. Метод динамического программирования Р.Беллмана  Любой конечный участок оптимальной траектории явл тоже оптимальной траекторией. Этот принцип опт-ти справедлив для сис-м у к-ых опт-ная траектория не зависит от предистории системы, а целиком определяется исходным её состоянием. Предположим, что речь идёт о цифровой сис-ме с квантованием по уровню и по времени. Требуется найти закон управления U(t) с учётом ряда ограничений, переводящий объект из состояния х(0) в с. Х(tn) при условии обеспечения минимума критерия оптимальности в виде функционала. Для дискретной системы с квантованием по времени Q=∫0tn G(X,U)dt можно записать в виде Q=Σ (n=0 m)G{X[n],U[n]} (1) Введено относительное время n – текущий № шага во времени, к-ый = периоду квантования. Задача заключается в опред-нии управления U[n] в виде последовательности значений U[0], U[1]… U[m-1], каждое из которых может имеет 1 из l дискретных значений. Это управление U[n] должно минимизировать сумму (1). Должны быть заданы ограничения на U и X, входе и выходе Будем искать решение двигаясь с конечного момента времени t=tn, n=m Найдём и запомним оптимальное значение управляющего воздействия U[m-1] в начале последнего интервала для каждого возможного дискретного значения Х [m-1]. Одновременно запоминаем и соответствующее значение приращения ∆Qm-1 – критерий оптимальности. В рез-те нах опт-ное значение ∆Qm-1 и U[m-1] и запоминаем, как функции. Переходим к началу [m-2] шага, нах ∆Qm-2 за 2 последних шага и соотв-щее опт-ное значение U[m-2], как ф-цию вых величины системы Х [m-2]. Для каждого значения U[m-2] сперва нах приращение критерия за 2-й шаг и значение Х [m-1] в конце 2го шага. После этого опред-ем полное приращение ∆Q[m-2] за 2 шага. Переходя далее к началу [m-3] шага и тд попадаем в начальную точку x[0].Опред-в при этом оптим-е управление U[n] и сам оптим-ый процесс x[n] и суммарную величину критерия оптимальности Q. Оптимизация функционала зависящего от искомой ф-ции U[n] заменяется последовательностью n-оптимизаций, значительно более простой функции ∆Q[m-i] одной переменной U[m-i] 24. Синтез оптимальных САУ. Оптимальные САУ могут быть 2ух типов: Разомкнутые и замкнутые. В простейшем случае когда внешнее воздействие известно можно построить оптимальное САУ в виде разомкнутой системы. ПУ – программное устройство.ИУ – исполнительное устройство.О – объект управления. Пример: вывод (калич.) объекта на орбиту. Синтез таких САУ сводится к синтезу оптимальной программы управления v(t), которое заранее вводится в ПУ. Если внешнее воздействие неизвестно, но их можно оперативно измерить, то оптимальный процесс может быть реализован в виде системы: F попадает не только на О но и измеряется чувствительным устройством.  Штрих пунктиром показаны данные о состоянии объекта до начала очередного процесса управления (ввода начальных условий). Штрих пунктиром показаны данные о состоянии объекта до начала очередного процесса управления (ввода начальных условий).Пример: САУ курса самолета или корабля, где в качестве ВУ используется бортовая ЦВМ. Синтез оптимальной замкнутой САУ заключается в нахождении оператора управляющего воздействия в виде зависимости v(t), обеспечивающее оптимальный процесс х(t) на выходе при заданных внешних воздействиях и начальных условиях.  В таких системах осуществляется оптимальное управление вне зависимости от характера изменения воздействия во времени. В общем случае зависимость v(x), является нелинейной. 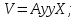 Ayy – оператор (нелинейной) УУ.В наиболее общих случаях, является комбинир. Системами, в которых управление осуществляется как функция от Х, так и от внешних воздействий. V=V(X,F,G) Ayy – оператор (нелинейной) УУ.В наиболее общих случаях, является комбинир. Системами, в которых управление осуществляется как функция от Х, так и от внешних воздействий. V=V(X,F,G)Такие системы состоят из разомкнутой системы оптимального программного управления и замкнутой САУ, устраняющей отклонения от прописанного программой оптимального режима работы объекта, вызвана различными причинами. Критерии оптимальности для синтеза программы разомкнутого и замкнутого управления могут быть различными. Например в случае синтеза автопилота летающего аппарата, программа управления может быть оптимизирована по условию минимальности топлива, а замкнутой системы по критерию качества переходного процесса. 25. Оптимальные САУ при случайных воздействиях. Так как информация о состоянии объекта и внешних воздействиях не всегда доступна, приходится переходить к статистическому представлению воздействий. Отсюда, управление в статистическом смысле, т.е. не для каждого процесса управления отдельно, а в среднем для всего множества его реализаций. В таких САУ качество управления хуже. Часто в качестве критериев берут среднее значение – мат.ожидание M[tn]. Если требуется минимизировать ошибку управления, в качестве статистического критерия оптимальности берут среднее значение квадрата отклонения X(G), т.е. дисперсию. M{[X(t)-G(t)]2} В задачах подобных задаче обнаружения сигнала, т.е. определения факта его наличия. В качестве минимизирующего критерия применяется вероятность ошибочного решения. Тогда условие оптимальности: Рош=Рлс+Рпс=min (1) Рлс – вероятность обнаружения ложного сигнала Рпс – вероятность потери сигнала Критерий Котельникова (идеального наблюдателя). Применяется при решении задачи на поражение цели, если существенен только факт попадания, а не величина ошибки (в виде отклонения от центра цели). В ряде случаев 2 составляющие формулы (1) представляют собой существенно не одинаковую опасность, при чём ЛО более нежелательна, тогда критерий дополняют условием, что Рло д.б. снижена до определённого допустимого уровня. Рло=С Он превращается в условную вероятность оптимального решения. Рпс=min Рло=С (2) – Критерий Неймана-Пирсона Перечисленные критерии м.б. объединены в критерий среднего риска: ρ(А)=M[l(G,X)] – min ρ(А) – средний риск, l(G,X) – некоторая функция (G – задание, X – реализация на выходе системы – функция потерь), А-некоторый оператор системы, связывающий G и X. Такие задачи получили название Байесовских. Минимаксный критерий оптимальности. Подход основан на критерии в виде максимального условного риска, т.е. max ρ(А/G)=min – условие минимизации максимального риска G Максимальное значение по G от ρ(А/G), из всех его значений соответствующих всем возможным значениям G. Минимизация максимального значения условного риска из всех значений соответствующих различным G. Получение наилучшего результата в наихудшей ситуации. 26. Классификация адаптивных систем. Самонастраивающиеся САУ. Ад-ные (приспосабливающиеся) системы – сис-мы, к-ые автоматически приспосабливаются к изменению внешних условий и свойств объекта управления. Обеспечивая при этом необходимое качество управления, путём изменения структуры, и параметров управляющего устройства. Качество управления численно определяется критерием качества I – оценивает наиболее важный показатель САУ. I – функционал зависящий от входных и выходных величин системы. В отдельных случаях I – функция. Примеры: самолёт, ракета  Q - Объект управления, УУ - управляющее устройство (УУо основное у-во, УУа у-во адаптации), УУа управляет УУо изменяя его оператор, т.е. схему и значение параметров, в соответствии с изменением внешних условий работы и св-в объекта, для этого УУа измеряет в самом общем случае внешние воздействия F и G и вых и вх величины объекта, вырабатывается сигнал У, определяется критерий качества управления I от функции этих 4-х параметров I(X,U,G,F) В зависимости от алгоритма работы УУа определяет отклонение критерия качества I от заданного или от экстремального его значения и воздействует на УУо макс-но, чтобы ликвидировать это отклонение. Выделяется 2 контура управления: основной и адаптации. Автоматическая адаптация выполняемая УУа может осуществляться в виде разомкнутой, замкнутой и комбинированной системы. Система адаптации может работать постоянно, периодически и однократно. Адаптивные САУ: со стабилизацией, с оптимизацией качества управления. Самонастраивающиеся САУ со стабилизацией качества управления. Адаптация заключается в стабилизации заданного критерия качества I путём изменения настройки УУо. Служат для стабилизации динамических св-в системы. Критерии кач-ва в этом случае косвенные (корневые, частотные, интегральные) Используются и статистические критерии качества в виде средне квадратического отклонения. Непосредственно динамические характеристики объекта (частотные, переходные хар-ки) Самонастраивающиеся САУ с оптимизацией качества управления. САУ экстремальные самонастраивающиеся. В отличии от САУ со стабилизацией, в этих САУ з-чей самонастройки явл-ся поддержание оптимального значения критерия качества управления I. Т.о. УУа будет решать задачу оптимизации автоматич-ки, к-ую однократно решает конструктор неадаптивной опт-ой сис-мы, при её конструировании, или периодически оператор-настройщик в ходе эксплуатации системы. Основой такой автоматич-й оптим-ции явл-сяавтоматич-й поиск оптимального оператора УУо, но сущ-ют и безпоисковые САУ с автомат-й оптимизацией. Принцип действия таких САУ зависит от того какой режим сис-мы хар-ся принятым критерием кач-ва: динамич-м или статич-м. Различают САУ с оптим-цией динамических режимов и статических. 27. Самоорганизующиеся Сау. Адаптивные Сау – системы, которые автоматически приспосабливаться к изменения внешних условий и свойств объекта управления, обеспечивая при этом необходимое качество управления путем изменения структуры и параметров УУ. Это адаптивный САУ, в которых адаптация осуществляется путем изменения оператора, т.е структурной схемы (УУОсновной). Эту САУ можно представить такой же схемой как и самонастраивающийся, однако здесь воздействие y на стороны УУадаптации на УУосновные вызывает изменение не численного значения параметров, а изменение структурной схемы УУосновные, поэтому их еще называют системы с переменной структурой.  У них сигнал У является дискретным сигналом, каждому значению которого соответствует определенный оператор т.е определенный алгоритм управления объектом. Пример: система управления противовоздушной обороны, робот |
