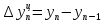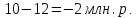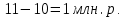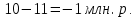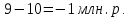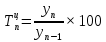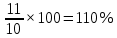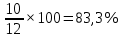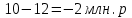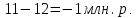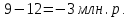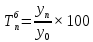СТОХАСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ. 1 Теоретические основы моделей временных рядов
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
1 2 Содержание
Введение Моделирование в научных исследованиях стало использоваться еще в глубокой древности и постепенно захватывало все новые области научных знаний. В современном мире на помощь пришли компьютерные технологии, а именно компьютерное моделирование, позволяющее создать и увидеть «виртуальные» эксперименты, модели, а также и стохастические процессы. Методы численного моделирования случайных процессов и полей находят широкое применение при решении теоретических и прикладных задач в различных областях науки и техники, причем область применения этих методов и сложность решаемых на их основе задач постоянно увеличиваются. В статистической метеорологии, климатологии, океанологии, гидрологии применение этих методов показало их высокую эффективность при решении широкого класса задач, включающего задачи усвоения гидрометеорологической информации, задачи, связанные с исследованием вероятностных свойств реально наблюдаемых процессов, вероятностным прогнозированием, исследованием свойств статистических оценок, синтезом динамических и вероятностных методов описания реальных процессов и т.д. Исходным пунктом для решения этих задач является построение вероятностных моделей реальных процессов и полей. Под численной вероятностной моделью реального временного ряда обычно понимают искусственную случайную последовательность, которая по некоторому набору заранее выбранных вероятностных характеристик совпадает с наблюдаемой. Аналогично определяется вероятностная модель реального поля на регулярной или нерегулярной сетке либо в произвольной точке заданной области. Теория стохастических или случайных процессов является одной из немногих специализированных математических теорий, востребованной и общей в различных науках. В тоже время не все явления и процессы можно представить с помощью функциональных зависимостей. В таких случаях моделируются и изучаются стохастические связи. Целью данной работы является изучение стохастического моделирования и прогнозирования временных рядов. Для достижения данной цели можно выделить ряд задач: 1. Рассмотрение понятия временного ряда; 2. Изучение методов обработки временных рядов; 3. Описание основных методов анализа и прогнозирования временных рядов; 4. Изучение стохастического прогнозирования временных рядов. В ходе исследования применялись следующие методы: анализ, моделирование, изучение научной литературы и ее обобщение. 1 Теоретические основы моделей временных рядов 1.1 Понятие временного ряда В настоящее время для изучения свойств сложных систем, в том числе и при экспериментальных исследованиях, широко используется подход, основанный на анализе сигналов, произведенных системой. Это очень актуально в тех случаях, когда математически описать изучаемый процесс практически невозможно, но в нашем распоряжении имеется некоторая характерная наблюдаемая величина. Поэтому анализ систем, особенно при экспериментальных исследованиях, часто реализуется посредством обработки регистрируемых сигналов. Например, в аритмологии в качестве такого сигнала используется электрокардиограмма, в метеорологии – данные метеонаблюдений и т.п. Обычно такой сигнал называется наблюдаемой, а метод исследования – реконструкцией динамических систем. Этот раздел теории динамических систем называется анализом временных рядов. Наблюдаемая – это последовательность значений некоторой переменной (или переменных), регистрируемых непрерывно или через некоторые промежутки времени. Часто вместо термина наблюдаемая используется понятие временной ряд. Ясно, что наличие только лишь временного ряда вместо полного решения уравнений сильно ограничивает наши знания об изучаемой системе. Это налагает большие ограничения на возможности метода реконструкции. Задача идентификации при анализе наблюдаемых предполагает ответ на вопрос, каковы параметры системы, породившей данный временной ряд – размерность вложения, корреляционная размерность, энтропия и др. Размерность вложения – это минимальное число динамических переменных, однозначно описывающих наблюдаемый процесс. Корреляционная размерность является оценкой фрактальной размерности аттрактора системы и частным случаем обобщенной вероятностной размерности. Понятие энтропии связано с предсказуемостью значений ряда и всей системы. Задача прогноза имеет целью по данным наблюдений предсказать будущие значения измеряемых характеристик изучаемого объекта, т.е. составить прогноз на некоторый отрезок времени вперед. Сейчас разработано и обосновано несколько различных методов прогноза. Однако все они подразделяются на на два основных класса: локальные и глобальные. Такое деление проводится по области определения параметров аппроксимирующей функции, рекуррентно устанавливающей следующее значение временного ряда по нескольким предыдущим. Многочисленные приложения анализа временных рядов составляет в настоящее время бурно развивающуюся область науки. Временной ряд — последовательность регистрируемого сигнала (наблюдаемая). Такой подход используется, когда нет возможности построить уравнения движения. Примеры: солнечная активность, землетрясения, ЭЭГ, ЭКГ, биржевой курс и т.п. Рассмотрим задачи, которые здесь возникают. Физика солнца: а) скрытые периодичности; б) прогноз активности. Электрокардиограммы (ЭКГ): а) природа наблюдающихся аритмий; б) прогноз развития состояния. Экономические ряды: а) задача сегментации; б) задача прогноза. Химическая кинетика: а) анализ динамики; б) построение модели. Рассмотрим возможность прогнозирования динамики изучаемой системы по порождаемому временному ряду и на основе этого возможность предложения модели. Теория Такенса: 1) Определить, динамическая ли система (конечность степеней свободы системы, порождающей ряд) → размерность вложения. 2) Горизонт прогноза: энтропия временного ряда. 3) Точность прогноза. Рассмотрим описание процессов временными рядами. Аттрактор — «притягатель». Странный аттрактор — не многообразие (отличен от конечного объединения подмногообразий). Отсюда название «странный». Характеристики «странности»: те же, что для канторовых множеств. Фрактальные множества в природе: медицина (капилляры, бронхи); осаждение ионов металла на затравочном образце; электрический разряд (фигура Лихтенберга); самоподобные явления на бирже. Основной вывод: существует универсальность в описании многих явлений, хотя, конечно, при помощи фрактального подхода описать можно далеко не все. Анализ рядов, порожденных системами, на основе спектров → «спад» сглаженных спектров. Тогда можно обнаружить аналогии с шумами: шум белый шум розовый шум коричневый шум черный Это поясняет приведенный ниже рисунок. Хорошо видно, что наблюдаемые значения группируются. Иными словами, в белом шуме за определенный (небольшой) интервал времени имеется примерно одинаковое количество положительных и отрицательных значений. Для коричневого процесса это не так: значения, если они положительные, некоторое время и останутся таковыми (они кластеризуются), т.е. не следует быстро ожидать, что они станут отрицательными. Вероятность этого для коричневого и черного шумов мала. 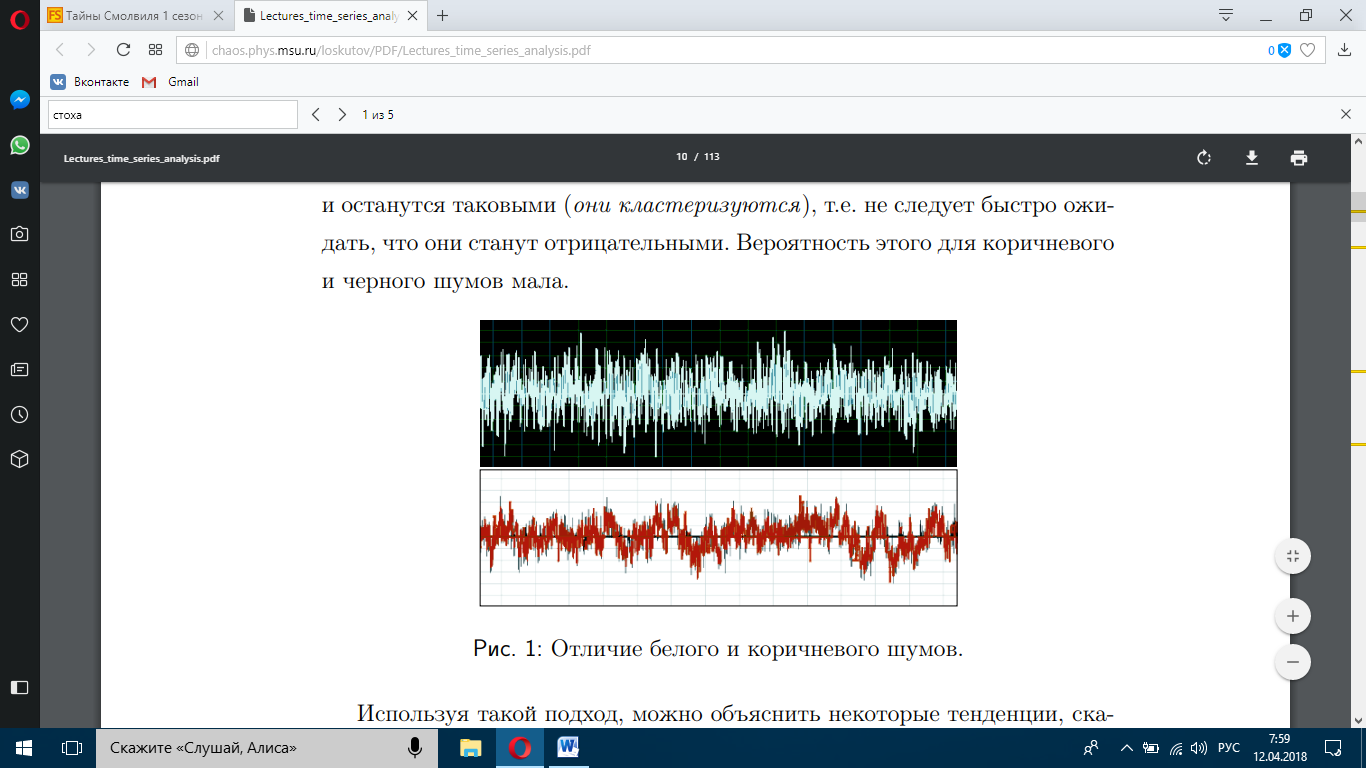 Рис. 1: Отличие белого и коричневого шумов. Используя такой подход, можно объяснить некоторые тенденции, скажем, в экономике и на биржах. Например, попав в какой-либо из кластеров, практически невозможно выйти из него быстро ⇒ после спада не следует ожидать быстрого подъема . В азартных играх: если капитал упал до нуля, то вероятность того, что он в течение короткого промежутка времени восстановится, практически нулевая. Отсюда можно строго обосновать стратегии: жадного игрока (быстро получить прибыль); беспечного игрока (ставить почти все деньги); робкого игрока (играет по маленькой); опытного игрока (использует побочные сведения). Кроме того, в случае действия группы фирм на рынке, можно обосновать: стратегию разорения конкурентов (это может быть не очень выгодно, т.к. останешься один); стабилизация прибыли варьированием инвестиций. Это все существует в условиях хаотического развития ситуации. Поэтому сначала уместно напомнить основные положения теории хаоса. 1.2 Методы обработки временных рядов Несмотря на то, что нелинейные системы могут значительно отличаться в конкретных проявлениях и деталях, существуют глубокие аналогии в их организации и функционировании. Это предопределило интерес к методам, которые развиваются в рамках теории динамических систем, как универсальному инструменту исследования объектов самой различной природы. Наиболее явно такой объединяющий подход проявляется при анализе временных рядов. В настоящее время существует два качественно различных подхода к исследованию временных рядов: статистические динамические К статистическим подходам относятся вероятностные модели. К динамическим – теория Такенса (Такенса-Мане). Современно представление о возможности описания наблюдаемых дает т.н. эмбедология (от англ. embedding – вложение), объединяющая элементы теории размерности, теории информации, топологии, дифференциальной динамики и теории динамических систем. Рассмотрим подробнее статистические методы обработки временных рядов. Основа: имеется ряд yn и шум — последовательность некоррелирующих и одинаково распределенных случайных величин ξi с нулевым средним. Тогда можно записать, что 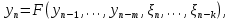 где k и m — некоторые конечные числа. Основные модели здесь – модели типа ARMA (Auto Regression Moving Average — авторегрессия скользящего среднего): 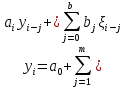 Нахождение искомых коэффициентов — это возможное решение задачи идентификации, а само соотношение для yi можно использовать для прогноза по m предыдущим. Это все линейные модели. В качестве прогнозируемой величины обычно используют среднее значение: 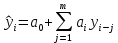 и предшествующие значения известны точно. Следует подчеркнуть, что шум является неотъемлемой частью модели; в его отсутствие поведение абсолютно непохоже на исследуемый ряд. Модели типа ARMA — это линейные модели. Часто строят нелинейные статистические модели (NARMA). Они делятся на параметрические и непараметрические. Параметрические модели: функция F 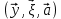 одна и та же для всех одна и та же для всех 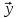 и и 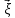 . Несколько параметров . Несколько параметров 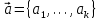 необходимо найти по временному ряду. Непараметрические модели: набор { необходимо найти по временному ряду. Непараметрические модели: набор {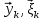 } в окрестности которого ис- пользуется локальная аппроксимация. Таким образом, при данных подходах часто используется интуиция, на основе которой тем или иным уравнением ставятся в соответствие определенные ситуации, а параметры неизвестны. } в окрестности которого ис- пользуется локальная аппроксимация. Таким образом, при данных подходах часто используется интуиция, на основе которой тем или иным уравнением ставятся в соответствие определенные ситуации, а параметры неизвестны.Следующая задача – выписать детерминированные уравнения для средних. Это – типичная теория случайных процессов. Основная трудность – удаление тренда (средние не зануляются, когда есть тренд), получение статистических оценок, фильтрация шума. Если случайный процесс не стационарен – используются ARCH-модели. В случаях, требующих быстрого обновления прогноза на основе вновь поступивших данных, используются адаптивные методы прогноза. К ним относится, например, метод экспоненциального сглаживания (метод Брауна). Следуя ему, каждому значению ряда в процессе идентификации модели присваивается весовой коэффициент, экспоненциально убывающий со временем, отделяющим это значение от последнего известного значения ряда. Таким образом, самые «старые» значения ряда практически не влияют на результаты прогноза, тогда как последние известные величины имеют наибольший вес. Тем самым этот метод приближается к локальным методам, так как основной вклад при прогнозе дает лишь небольшая часть самых последних по времени значений ряда. Методы авторегрессии разработаны наиболее тщательно и применяются, как правило, в прикладных задачах. Они реализованы практически во всех программных пакетах статистической обработки данных. Рассмотрим динамические методы обработки временных рядов. В статистических методах обработки используется допущение, что всегда имеется шум. Это довольно сильное условие. Поэтому мы должны априори полагать, что изучаемый ряд – стохастический. Возникает вопрос, допустим ли такой подход, если это детерминированный хаос и может в этом случае лучше работают другие методы. Здесь надо очень хорошо себе представлять отличие стохастичности от хаоса. Статистические методы не позволяют отличить конечномерный процесс от бесконечномерного, но это вполне можно сделать динамическими методами. Для многих систем конечномерное описание вполне допустимо. Так, в финансовых рядах число спекулянтов всегда конечно, другое дело, как те или иные их них влияют на процесс (сильно, слабо). Дискретное (конечномерное) описание здесь подразумевает выявление числа крупных спекулянтов. Тогда присутствие остальных можно рассматривать как влияние некоторого шума (его можно оценить, выявив попутно скрытые динамические процессы, ответственные за крупных игроков). Отсюда – смешанное описание: статистическое и динамическое. Первый вопрос, которым мы задаем, – определение возможности конечномерного описания, т.е. в приложении к конкретным рядам – вопрос о количестве факторов, влияющих на динамику. Это можно сделать посредством нахождения размерности вложения – минимального числа динамических переменных, однозначно описывающих поведение исследуемой системы. 2 Стохастическое моделирование и прогнозирование временных рядов 2.1 Основные методы анализа и прогнозирования временных рядов Основными статистическими методами исследования временных рядов являются: метод выделения тренда (временного сглаживания), регрессионный, автокорреляционный, адаптивный (скользящих средних), метод гармонического анализа, сингулярного спектрального анализа, бутстрепа (численного размножения выборок) и нейросетевой. Ниже кратко описывается идеология этих методов, даются основные определения из математической статистики и приводятся базовые уравнения соответствующих моделей. Случайным процессом на некотором вероятностном пространстве называется семейство случайных величин x(t), принимающих значения из множества, называемого областью определения процесса. Если параметр t принимает дискретные значения, то процесс называется временным рядом. Временной ряд называется стационарным в широком смысле, если его математическое ожидание не зависит от времени t, а корреляционная функция, являющаяся математическим ожиданием произведения отклонений значений ряда от среднего в различные моменты времени t1 и t2 зависит только от разности t1-t2. Более общее определение предполагает независимость от времени центральных моментов ряда вплоть до некоторого конечного порядка. Временной ряд x(t) называется стационарным в узком смысле, если при любых t и τ случайная величина x(t) распределена одинаково с величиной 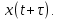 В настоящей работе используется определение стационарности в широком смысле, если речь идет о моментах ряда, и в узком смысле, если о его распределении. Рассмотрение существующих подходов к анализу временных рядов начнем с метода временного сглаживания или выделения тренда. При исследовании временных рядов принято выделять несколько составляющих: В настоящей работе используется определение стационарности в широком смысле, если речь идет о моментах ряда, и в узком смысле, если о его распределении. Рассмотрение существующих подходов к анализу временных рядов начнем с метода временного сглаживания или выделения тренда. При исследовании временных рядов принято выделять несколько составляющих: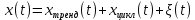 где 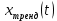 – плавно меняющаяся компонента, определяемая долговременной тенденцией (трендом) изменения ряда признаков, – плавно меняющаяся компонента, определяемая долговременной тенденцией (трендом) изменения ряда признаков, 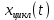 - циклическая или сезонная компонента, которая отражает повторяемость процессов на определенных промежутках времени, a - циклическая или сезонная компонента, которая отражает повторяемость процессов на определенных промежутках времени, a 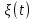 - случайная компонента, содержащая влияние прочих факторов, механизм которого (влияния) скрыт от наблюдателя. Первые две составляющих (тренд и цикл) в идеале должны быть описаны точно, т.к., это закономерные факторы, изучаемые в рамках детерминистских моделей. Однако следует заметить, что сами детерминистские модели представляют определенную идеализацию описываемых закономерностей, поэтому им также присуща некоторая неточность. В этом смысле представление (1) несколько условно, но оно бывает полезно на практике для интерпретации результатов статистического анализа данных. - случайная компонента, содержащая влияние прочих факторов, механизм которого (влияния) скрыт от наблюдателя. Первые две составляющих (тренд и цикл) в идеале должны быть описаны точно, т.к., это закономерные факторы, изучаемые в рамках детерминистских моделей. Однако следует заметить, что сами детерминистские модели представляют определенную идеализацию описываемых закономерностей, поэтому им также присуща некоторая неточность. В этом смысле представление (1) несколько условно, но оно бывает полезно на практике для интерпретации результатов статистического анализа данных.Трендовая компонента временных рядов обычно не известна точно, а, как и ряд в целом, является случайной величиной, но ее изменение из некоторых априорных суждений часто может быть качественно описано аналитически. Для описания тренда используются так называемые кривые роста, которые позволяют моделировать процессы трех основных качественных типов: без предела роста, с пределом роста без точки перегиба, а также с пределом роста и точкой перегиба. Процессы развития без предела роста характерны в основном для абсолютных объемных показателей. Процессы с пределом роста характерны для относительных показателей, таких, как душевое потребление продуктов питания, внесение удобрений на единицу площади, затраты на единицу произведенной продукции и т.п. Для моделирования этих процессов используются полиномиальные или квазиполиномиальные (с экспоненциальными множителями и т.п.) зависимости, дробно-рациональные и линейно-логарифмические функции, кривые Гомперца и иные функциональные зависимости. В рамках многопараметрических моделей, часто бывает возможно провести аппроксимацию данных с требуемой точностью, однако этот подход не всегда удовлетворителен при прогнозировании, поскольку подбираемые функции не обязательно отражают реально обусловленную зависимость наблюдаемой величины от времени. Таким образом, часто используемым методом моделирования нестационарных временных рядов является параметрическое оценивание. В этом случае подбираются параметры той или иной функциональной зависимости для трендовой составляющей, после исключения которой, остается стационарный ряд. Оставшийся ряд может и не быть стационарным в смысле математического определения этого понятия, но на практике его удобно считать таковым с доверительной вероятностью, достаточной для исследователя. Для этой цели используются различные тесты на стационарность, которые, как правило, разработаны для применения к известным функциональным зависимостям (например, нормального, экспоненциального или равномерного распределений). В частности, для нормально распределенных случайных величин тест на наличие тренда проводится в основном по критериям Стьюдента и Фишера , но также существуют и другие тесты, использующие нормальность распределения. Например, статистики критерия Фостера-Стюарта для обнаружения тренда в среднем значении и дисперсии используют производные случайные ряды из нулей и единиц, определяющие наличие тренда в максимумах или минимумах исходного ряда. Если нет оснований предполагать нетривиальную функциональную зависимость трендовой составляющей ряда, ее часто считают полиномиальной. В этом случае такой тренд может быть исключен путем перехода к первым, вторым и т.д. разностям в значениях ряда, т.е. вместо ряда x(t) можно рассмотреть ряд 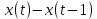 или ряд из разностей более высокого порядка, называемый производным рядом. Такой метод достаточно эффективен, если функциональный тип тренда сохраняется во времени. или ряд из разностей более высокого порядка, называемый производным рядом. Такой метод достаточно эффективен, если функциональный тип тренда сохраняется во времени.Целью сведения временного ряда к стационарному является появляющаяся тогда возможность использования теоремы Гливенко о сходимости эмпирической вероятности к распределению генеральной совокупности и критерия согласия Колмогорова о близости выборочной функции распределения и распределения генеральной совокупности для того, чтобы попытаться определить вид распределения, к которому относилась бы изучаемая выборка данных, после чего с известной доверительной вероятностью строить прогноз. Желание иметь дело со стационарным рядом вызвано также возможностью обосновать прогнозные модели для такого ряда применением теоремы Вальда о разложении, согласно которой всякий стационарный процесс может быть единственным образом представлен в виде суммы двух некоррелированных между собой процессов: детерминированного (сингулярного процесса), прогноз которого на любое время вперед безошибочен, и чисто случайного (регулярного белого шума, т.е. стационарного процесса, фурье-разложение которого является константой). Поэтому, хотя реальные процессы, как правило, не являются стационарными, тем не менее, возникает желание в первом приближении считать их таковыми. Такой подход может дать удовлетворительный результат в задачах краткосрочного прогнозирования. Ряды, которые после надлежащих приготовительных операций можно считать стационарными, далее изучаются методами регрессионного, корреляционного и гармонического анализов. Каждый из этих методов используется для создания некоторой прогнозной модели для изучаемых рядов. В зависимости от конкретной специфики ряда используются различные из перечисленных методов. Ниже кратко описаны их содержательные части. Линейная регрессионная модель позволяет связать две величины Y и X линейной зависимостью вида 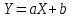 по имеющимся N парам значений по имеющимся N парам значений 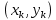 методом наименьших квадратов (МНК). методом наименьших квадратов (МНК).Обобщение линейной регрессионной модели на случай зависимости, возможно, нелинейной, от нескольких объясняющих переменных приводит к задаче выбора наиболее адекватной модели по числу переменных и виду регрессионных функций. Регрессионные модели применяются в основном тогда, когда объясняющая переменная (в данном случае это величина X) не является случайной, а автокорреляция между значениями другой (объясняемой величины Y) мала. Максимумы модуля автокорреляционной функции показывают наличие лагов, т.е. промежутков времени, на которых проявляется скрытая зависимость случайных величин. К примеру, в рядах с существенным влиянием циклической компоненты лаги выражены на графике выборочной автокорреляционной функции особенно сильно. Модели, использующие лаговую автокорреляцию, называются автокорреляционными (AM) или авторегрессионными. Последовательное усложнение автокорреляционных моделей привело к появлению т.н., адаптивных моделей прогнозирования, которые базируются на объединении двух схем - скользящего среднего (СС) и авторегрессии. Модель СС состоит в том, что для определения свойств временного ряда с целью краткосрочного прогноза берется выборка последних данных за некоторый промежуток времени Т. Модификацией модели СС является взвешенная схема СС, когда оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т.е., информационная ценность наблюдений признается тем большей, чем ближе находятся они к концу интервала наблюдений. Возможны также варианты, когда наибольшую ценность имеют наблюдения с определенным лагом. Другим типом адаптивных прогнозных моделей является параметрическая модель сглаживания, когда значение в момент 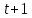 определяется не только статистиками самого ряда, но и прогнозом этого ряда за несколько предшествующих моментов времени, а также оценками текущих трендов (модели Брауна, Хольта и Уинтерса), Как правило, адаптивные модели применяются для прогнозирования ряда на один шаг вперед. определяется не только статистиками самого ряда, но и прогнозом этого ряда за несколько предшествующих моментов времени, а также оценками текущих трендов (модели Брауна, Хольта и Уинтерса), Как правило, адаптивные модели применяются для прогнозирования ряда на один шаг вперед.Одним из методов выделения т.н. главной части или главных компонентов временного ряда является метод сингулярного спектрального анализа, разработанного в теории нелинейных динамических систем и представляющего оригинальный подход к исследованию автокорреляционной зависимости. Из других - «нетрадиционных» методов анализа временных рядов - следует отметить нейросетевой метод и метод размножения выборок. Нейросетевой метод анализа случайных процессов является одним из активно разрабатываемых в последнее время. Он, как и большинство описанных выше методов, направлен на отыскание корреляционной связи между элементами временного ряда. Целью метода является отыскание «предвестника» наступления того или иного события и определение вероятности последнего. Главной задачей является «обучение» искусственной нейронной сети на достаточно большом количестве выборок некоторого объема, после чего принятие решения о наличии «предвестника» принимается сетью на основе эмпирической вероятности наступления похожих случаев в период «обучения». Нейросетевые методы используют математическую модель нейронных сетей, на основе которых функционирует мозг человека и других живых существ. Основу сети составляет нейрон- устройство, имеющее вход, преобразующее полученный сигнал и передающее его на выход, дальше по сети, нейронам, соединенным с ним. Настройкой сети к применению служит обучение – сеть обучается на основе известных примеров (значений ряда), получая поощрения за правильный ответ (к примеру, прогноз) или ответ в пределах точности и наказание за ответ неправильный. Таким образом, получающийся ответ носит вероятностный характер. Особенностью нейросети является то, что создатель не должен знать закономерностей ряда при обучении сети, она обучается сама, на примерах. В этом же заключается и слабое место - сеть может выдавать очень точные ответы без указания, как они получились, представляя собой «черный ящик». Нейросетевой подход зачастую бывает очень эффективным в случаях, когда другие методы несостоятельны, является толерантным к приемлемому количеству ошибочных обучающих примеров, однако имеет и слабые стороны. К ним относятся относительность выдаваемых ответов, высокая вычислительная стоимость обучения, отсутствие гарантий приемлемости результата применения метода. Метод размножения выборки является одним из методов случайной обработки данных стационарных процессов. Его сущность состоит в том, что по имеющимся N наблюдениям за случайной величиной, образующим по предположению выборку из генеральной совокупности, строится выборочная функция распределения, из которой извлекаются выборки с возвращением того же объема N с равными вероятностями извлечения каждого значения. По каждой выборке строится оценка интересующего параметра исходной случайной величины, а затем полученные оценки усредняются. Из проведенного рассмотрения следует, что ни одно из перечисленных основных направлений статистического анализа временных рядов не является универсальным: конкретный случайный процесс лучше всего моделируется методом одного из направлений. Нет утверждения о том, что некоторый метод при своем практическом применении дает наименьшую ошибку прогнозирования для любых временных рядов. Напротив, каждый из методов имеет определенные ограничения, препятствующие их эффективному применению к задачам прогнозирования. 2.2 Стохастическое прогнозирование временных рядов В зависимости от области определения параметров аппроксимирующей функции выделяют две основные группы методов: глобальные – параметры аппроксимирующей функции идентифицируются посредством использования всех известных значений ряда. Основное приложение – получение глобальных характеристик системы. К ним относятся: авторегрессионные модели, сингулярный спектральный анализ. локальные методы основаны на принципе локальной аппроксимации (LA). Применяется в целях прогнозирования динамики ряда. Преимущества локальных методов прогноза нерегулярных (хаотических, квазипериодических) рядов: применение не требует априорной информации о системе, породившей временной ряд; нет необходимости в построении специфической модели динамики исследуемого ряда; использования для прогнозирования наиболее близких к стартовой точке (стартовому вектору) значений ряда; использование меньшего количества исходных данных; горизонт прогноза ограничивается не возможностями метода, а особенностями динамики ряда. Метод сингулярного спектрального анализа (SSA) используется для определения основных составляющих временного ряда и подавления шума. Метод SSA позволяет: различать составляющие временного ряда, полученные из последовательности значений какой-либо величины, взятой через равные промежутки времени; находить заранее неизвестные периодичности ряда; сглаживать исходные данные на основе отобранных составляющих; наилучшим образом выделять компоненту с заранее известным периодом; предсказывать дальнейшее поведение наблюдаемой зависимости. В основе SSA лежит построение множества векторов задержек: 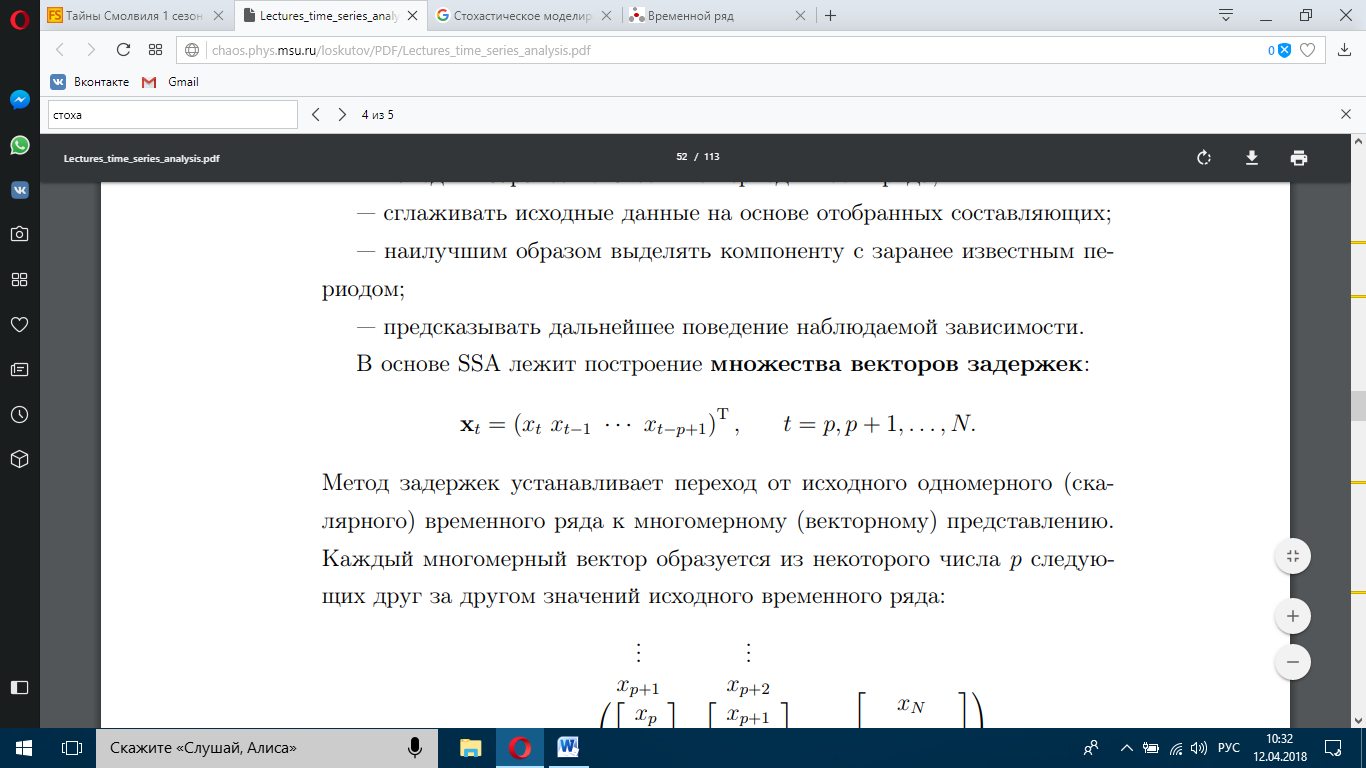 Метод задержек устанавливает переход от исходного одномерного (скалярного) временного ряда к многомерному (векторному) представлению. Каждый многомерный вектор образуется из некоторого числа p следующих друг за другом значений исходного временного ряда:  Здесь каждая квадратная скобка – вектор в p–мерном пространстве задержек; последовательность таких векторов задает матрицу задержек 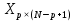 , где , где 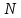 – число элементов исходного ряда. – число элементов исходного ряда.Особенностью SSA является обработка матрицы 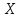 по алгоритму, похожему на метод главных компонент. Суть метода главных компонент состоит в снижении размерности исходного пространства факторов (задержек) с помощью ортогонального линейного преобразования. Полученные таким образом новые переменные и называют главными компонентами. Применение этого метода позволяет сгладить исходный ряд, снизить уровень случайных возмущений, повысить отношение сигнал/шум. по алгоритму, похожему на метод главных компонент. Суть метода главных компонент состоит в снижении размерности исходного пространства факторов (задержек) с помощью ортогонального линейного преобразования. Полученные таким образом новые переменные и называют главными компонентами. Применение этого метода позволяет сгладить исходный ряд, снизить уровень случайных возмущений, повысить отношение сигнал/шум.Способы прогнозирования на базе SSA следующие: (а) «Гусеница» и (б) метод авторегрессии, который применяется по отдельности к каждой из выбранных компонент разложения. Ниже представлены основные этапы применения SSA к конкретному ряду 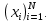 Рассмотрим прогноз методом SSA. На этом этапе строится ряд 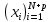 . При этом прогноз на p точек вперед осуществляется как применение p раз операции прогноза на одну точку. . При этом прогноз на p точек вперед осуществляется как применение p раз операции прогноза на одну точку.Базовая идея нахождения значения xN+1 состоит в следующем. Пусть имеется набор значений x1, x2, . . . , xN . Теперь построим выбор- ку в виде матрицы X. В качестве базиса поверхности, содержащей эту выборку, можно взять отобранные ранее собственные векторы V1 , V2 , . . . , vr матрицы C. Запишем параметрическое уравнение этой поверхности как 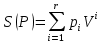 , где каждому значению вектора S(P), представляющего собой столбец высотой τ, соответствует набор из r параметров pi . Тогда k-му (k = 1, 2, . . . , n) столбцу исходной матрицы X соответствует свой набор значений параметров , где каждому значению вектора S(P), представляющего собой столбец высотой τ, соответствует набор из r параметров pi . Тогда k-му (k = 1, 2, . . . , n) столбцу исходной матрицы X соответствует свой набор значений параметров 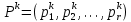 и, следовательно, и, следовательно,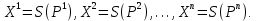 Для предсказания значения 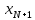 необходимо построить необходимо построить 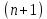 -й столбец -й столбец 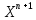 матрицы матрицы 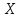 , которому соответствует некоторое значение параметров , которому соответствует некоторое значение параметров 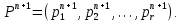 Этот набор параметров можно найти из соотношения Этот набор параметров можно найти из соотношения 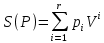 , исходя лишь из данных , исходя лишь из данных 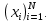 При этом прогнозируемый столбец будет записан следующим образом: При этом прогнозируемый столбец будет записан следующим образом: 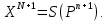 Как и в случае с отбором главных компонент, выбор значения τ существенным образом зависит от исследуемой проблемы. Пусть задача состоит в сглаживании ряда методом SSA, т.е. в восстановлении ряда с использованием известных периодичностей. Тогда выделение главной компоненты есть фильтрация ряда с переходной функцией фильтра в виде собственного вектора этой главной компоненты. Чем больше величина 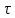 , тем больше параллельных фильтров, уже полоса пропускания каждого из них и лучше сглаживание ряда. , тем больше параллельных фильтров, уже полоса пропускания каждого из них и лучше сглаживание ряда.Если требуется определить неизвестные (скрытые) периодичности в наблюдаемой последовательности, то следует сначала взять как можно большее значение 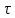 . Затем, после отбрасывания близких к нулю собственных чисел, величину задержки необходимо сократить. . Затем, после отбрасывания близких к нулю собственных чисел, величину задержки необходимо сократить.Предположим, что необходимо выделить одну известную периодическую компоненту. В этом случае следует выбрать значение 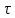 , равное искомому периоду. , равное искомому периоду.Наконец, пусть задача заключается в продолжении изучаемого ряда на заданную величину (т.е. в предсказании эволюции наблюдаемого процесса). Тогда следует взять максимально допустимое значение 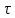 и затем подбирать величину и затем подбирать величину 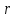 . .Задача. Определить вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные абсолютные приросты, темпы роста, темпы прироста, средний уровень ряда, средний темп роста, средний темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По расчетам сделать выводы. Графически изобразить полученный ряд динамики. Таблица 2.1. Данные задачи
Решение. Данный ряд динамики – интервальный, так как значение показателя заданы за определенный интервал времени.
1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||