разработка. ппппп. 1. теоретические сведения теоретические сведения к практической работе Описание множеств. Геометрическая интерпретация множеств
 Скачать 405.82 Kb. Скачать 405.82 Kb.
|
|
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Теоретические сведения к практической работе «Описание множеств. Геометрическая интерпретация множеств» Множество - совокупность элементов, объединенных некоторым признаком, свойством. Объекты, составляющие множество, называются его элементами. Множества обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают: а ∈ А ("а принадлежит А"). Если а не является элементом множества А, то записывают: а ∉ А ("а не принадлежит А"). Множества могут содержать как конечное число элементов, так и бесконечное. Множества, как объекты, могут быть элементами других множеств. Пустое множество - множество, не содержащее ни одного элемента, обозначается как ∅ либо { }. Универсальное множество (универсум) - все множества, участвующие в рассматриваемой задаче, обычно обозначается как U. Существует две формы задания множеств: перечисление элементов, то есть указание всех элементов множества, которые принято заключать в фигурные скобки: М = {1; 2; 3; 4; 5} . указанием характеристического свойства элемента - записью, из которой видна математическая зависимость принадлежности элементов множеству: Х = {х | Р(x)},где Р(х) – описывает свойства элементов х множества Х заданием порождающей процедуры. Мощность множества А — число различимых элементов множества А: |A| или n(A). Для мощностей имеются понятия: равенство, больше, меньше. Множества A и B считают равными, если они состоят из одних и тех же элементов. Не следует путать понятия «равномощность множеств» и «равенство множеств». Множество А является подмножеством множества В, если любой элемент, принадлежащий множеству А, принадлежит множеству В: А В Рассмотрим примеры решений задач по теме « Описание множеств» Пример №1 Определите, какие из ниже приведенных способов представления множеств являются наиболее точными: а) А1 ={a,b,c,d,e,f,g,a}; б) A2 ={10,15,20}; в) A3 ={y| yB}; г) A4 ={B,C,D,E}; д) A5 =β(U) ={Ø,{a},{b},{a,b}}, где U ={a,b}; e) A6 ={b,c,D} Решение: а) При перечислении элементов множества не следует указывать один и тот же элемент несколько раз. Поэтому правильная запись множества выглядит следующим образом: А1={a,b,c,d,e,f,g}; б) Представление множества A2 ={10,15,20} списком своих элементов формально правильно. в) Определение множества A3 ={y:| yB} заданием характеристического свойства его элементов («принадлежность множеству В») точно. г) Определение множества A4 ={B,C,D,E} списком правильно, т.к. элементами данного множества А4 являются множества B,C,D и E. д) Данное определение множества также верно, т.к. множество β(U) – множество всех подмножеств, состоящих из элементов множества U. е) Определение множества A6 ={b,c,D} также верно, т.к. представляет собой список из конечного числа элементов, где подмножество D состоит также из элементов. Пример 2: Задайте множество А = {1, 3, 5, 7, 9} характеристикой его элементов Решение: Каждый следующий элемент множества А является натуральным числом, больше предыдущего на 2 и не превышает 10, поэтому A={a| a N & a Пример 3: Перечислите элементы множества X= {x| - x2 +1=0} Решение: для решения задачи необходимо найти корни квадратного уравнения: -x2 +1= 0 x2 – 1=0 x1=1; x2 = -1 X={1,-1} Пример 4: Дано множество целых однозначных чисел, состоящее из чисел, кратных 3. это множество: 1. простым перечислением; 2. описанием его характеристических свойств Решение: Множество чисел, кратных 3 – это: В= В= Пример 5: Определите мощности множеств А={7,7,8,8,0,7,8}, В={математика}, С={} Решение: В множестве два неразличимых элемента считаются за один, поэтому n(А)=3. Элементы множестве, заданном перечисление, разделяются запятыми или двоеточием, поэтому n(B)= 1. {}- условное обозначение пустого множества, поэтому n(C)=0 Пример 6: Изобразите с помощь. Кругов Эйлера множество всех действительных чисел. Решение: 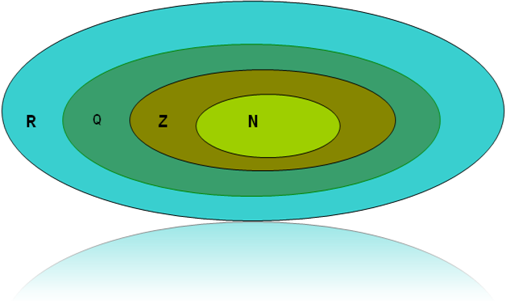 где: N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; R – множество действительных чисел. Теоретические сведения к практической работе «Операции над множествами» Если имеется два множества или более, то с ними можно выполнить операции пресечения, объединения, дополнения, разности, симметрической разности (Таблица 1) Таблица 1 «Операции над множествами» 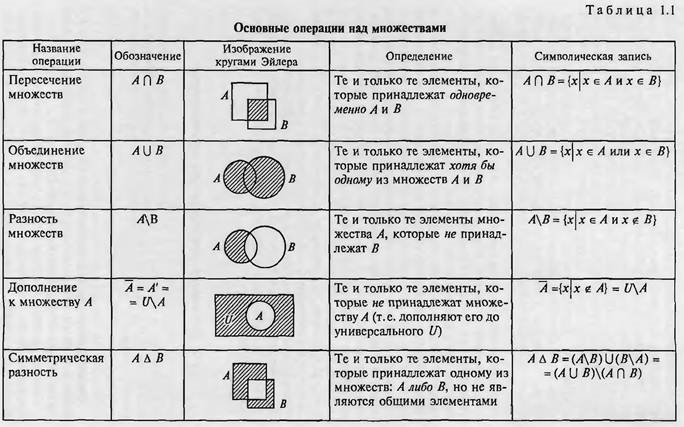 Основные законы и тождества, которым подчиняются операции объединения и пересечения: 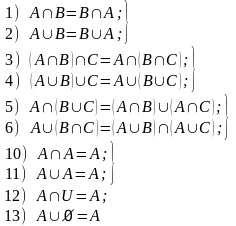 14) A 15) A∩=; Мощности пересекающихся и объединяющихся множеств вычисляются по формулам: U= Свойства абсолютного дополнения - A справедливо: Разность множеств можно выразить через операции отрицания и пересечения следующим образом: A\B = A¯B Частные свойства разности множеств: Если AB=, то А\В=А; Если AB, то А\В=; А\В = А\(АВ)’; A\A =; A\ =A. Рассмотрим примеры решений задач по теме « Операции над множествами» Пример 1: Даны множества A, B и C, которые представлены следующими элементами: A = {1, 2, 4, 5}, B = {1, 3, 5}, C = {4, 5, 6}. Какими элементами образованы все возможные пересечения этих множеств? Решение: Из определения пересечения следует, что из пересекающихся множеств в результирующее следует отобрать только те элементы, которые присутствуют во всех множествах одновременно. Тогда: 1) A ∩ B = {1, 2, 4, 5} ∩ {1, 3, 5} = {1, 5}; 2) A ∩ C = {1, 2, 4, 5} ∩ {4, 5, 6} = {4, 5}; 3) B ∩ C = {1, 3, 5} ∩ {4, 5, 6} = {5}; 4) A ∩ B ∩ C = {1, 2, 4, 5} ∩ {1, 3, 5} ∩ {4, 5, 6} = {5}. Пересечение трёх множеств, которое показано последним, логично получать поочерёдным пересечением каких-либо двух множеств (по ассоциативности этого действия). 4) (A ∩ B) ∩ C = ({1, 2, 4, 5} ∩ {1, 3, 5}) ∩ {4, 5, 6} = {1, 5} ∩ {4, 5, 6} = {5}. Пример 2: На диаграммах Эйлера-Венна изобразить результат операций, предварительно указав порядок действий в формуле. Р Порядок действий: 1. 2. 3. 4. Изобразим на диаграмме Эйлера–Венна: 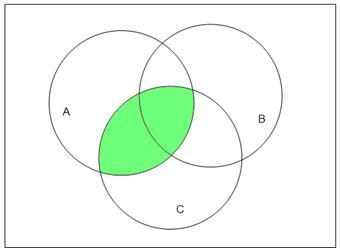 2. 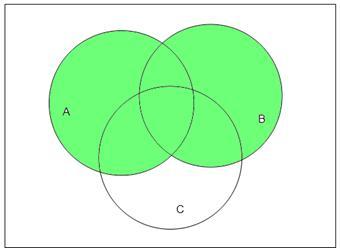 Пример 3: 3. 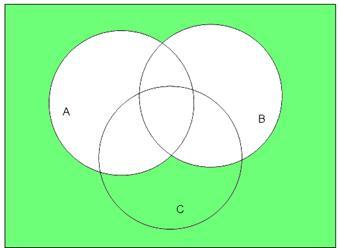 4. Упростить выражения, используя законы алгебры множеств Решение: . Пример 4: Пусть U – универсальное множество всех людей на Земле; А- множество людей, живущих в России; В – множество людей, не старше 18 лет; С – множество людей, учащихся в вузах. Каков содержательный смысл следующих множеств: а) АВ С б) А U в) В г) (АВ А д) В\А ? Решение: а) АВ С = множество людей, живущих в России, старше 18 лет и учащихся в вузах; б) АU = U - множество всех людей на Земле (св-во единицы); в) В = В (инволютивность) – множество людей, не старше 18 лет; г) (АВ А = А ( правило поглощения) – множество людей, живущих в России; д) В\А – множество людей, не старше 18 лет, не живущих в России. Пример 5: В одном городе Канады 70% жителей знают французский язык и 80% - английский язык. Сколько процентов жителей знают оба языка? Решение: Пусть А – множество жителей Канады, знающих французский язык,B - множество жителей Канады, знающих английский язык,С - множество жителей Канады знающих французский английский языки.Зная, что если два множества объединяются, то количество элементов окончательного множества находиться с помощью формулы включения / исключениявыражения: N(AB) = N(U) = N(A) + N(B) – N(AB) Тогда |A|=70, |B|=80, |U|=100. N(U)-N(A)=30%. N(U)-N(B)=20%. N(AB)=100%-(30%+20%)=50% - жителей городов Канады знают оба языка Пример 6: Из 37 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями. О посещении Большого театра с восторгом вспомнили 12 человек, Кремля - 14, а 16 - о концерте, по три студента запомнили посещения театра и Кремля, а также театра и концерта, а четверо – концерта и пребывания Кремле. Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле? Решение: Введем обозначения: А – множество студентов, вспоминающих о театре , n(A)=12; В – о Кремле , n(В)=14; С – о концерте , n (C )=16; D – множество всех студентов , побывавших в поездке. Изобразиммножества графически с помощью кругов Эйлера  Используем формулу включения/исключения для трех множеств: + n(A Обозначим n( , тогда 37-2=12 + 14 + 16 – 3 – 3 – 4- х, отсюда х=1 Теоретические сведения к практической работе «Отношения и операции над ними» Отношение – один из способов задания взаимосвязей между элементами множества. Задать отношение списком пар означает перечислить все пары элементов, для которых это отношение выполняется. Бинарное отношение – используется для определения каких-то взаимосвязей, которыми характеризуются пары элементов в множестве М. Свойства бинарных отношений: a). R – рефлексивно, если имеет место aRa для любого аМ (Например, отношение «жить в одном городе» - рефлексивно). б). R – антирефлексивно, если ни для какого а, аМ, невыполняется aRa. (Например, отношение «быть сыном» -антирефлексивно). в). R – симметрично, если aRb влечет bRa (Например, отношение «работать на одной фирме» - симметрично). г). R – антисимметрично, если aRb и bRa влечет a=b, т.е. ни для каких различающихся элементов a и b (ab) не выполняется одновременно aRb и bRa.(Например, отношение «быть сыном», «быть начальником» - антисимметрично). д). R – транзитивно, если aRb и bRc влечет aRc (например, «быть моложе», «быть братом» - транзитивно). Матрица отношений – это квадратная матрица, по вертикали и горизонтали которой перечисляются элементы множества. В справедливости некоторых из вышеуказанных свойств можно наглядно убедиться, построив матрицу для данного отношения и помня следующие правила: 1 Главная диагональ матрицы рефлексивного отношения содержит только единицы. 2 Главная диагональ матрицы антирефлексивного отношения содержит только нули. 3 В матрице симметричного отношения Сi,j = Cj,i, т.е. матрица симметрична относительно главной диагонали. 4 В матрице антисимметричного отношения отсутствуют единицы, симметричные относительно главной диагонали. Рассмотрим примеры решения задач Пример 1: Пусть М равно {2,5,-7,9,12,-15}. Составить матрицы и списки пар отношений R1, R2M2 , если R1 – «иметь сумму больше десяти», R2 – «иметь разность больше нуля». Решение: Список пар – это перечисление пар, для которых это отношение выполняется. Матрица – это квадратная матрица,по вертикали и горизонтали которой перечисляются элементы. множества и в которой элемент Сij , стоящий на пересечении i-ой строки и j-го столбца, равен единице, если между соответствующими элементами имеет место отношение R, или 0, если оно отсутствует. R1={ (2,9), (2,12), (5,9), (5,12), (9,9), (9,12), (12,12) }. R2={ (2,-7), (2,-15), (5,2), (5,-7), (5,-15), (-7,-15), (9,2), (9,5), (9,-7), (9,-15), (12,2), (12,5), (12,-7), (12,9), (12,-15) }. Пример 2: Пусть М={1,2,3,4,5,6,7}. Составить матрицу отношений R1 M2, если R1 – «иметь один и тот же остаток от деления на 7»; Решение: На пересечении i-ой строки и j-ого столбца ставим «1», если отношение R1 выполняется и «0» - если не выполняется. Например: а1=1; в2=2 1/7 2/7 С1,2 0
Пример 3: На рисунке представлено множество элементов. Задать списком пар отношения R1, R2, R3, R4, если: R1 – «быть внуком…». R2 – «быть двоюродными братьями». R3 – «быть прадедом…». R4 – «иметь общего сына». Решение: Список пар – это перечисление пар, для которых это отношение выполняется: R1={ (h,a), (g,a), (f,a), (e,a), (d,a), (n,b), (n,c), (m,c), (k,c) }. R2={ (f,e), (f,d), (g,e), (g,d), (h,e), (h,d), (k,m)}. R3={ (a,k), (a,m), (a,n) }. R4={ (h,g), (f,d) }. Пример 4: Найти декартовое произведение множеств А и В, если А={а,b,d }, B={ f,d,e }. Решение: Декартово произведение множеств А и В представляет собой множество всевозможных упорядоченных пар, в которых первые элементы принадлежат множеству А, а вторые — элементы принадлежат множеству В, следовательно, AB={ (a,f), (a,d), (a,e), (b,f), (b,d), (b,e), (d,f), (d,d), (d,e) }. Пример 5: Найти правую и левую область отношения: R={(1,2), (2,1), (3,1), (1,3), (3,5)} Решение: ЛевойобластьюДl отношенияRназываетсямножество всех первых элементов пар, принадлежащих R,правой областью Дr – множество всех вторых элементов этих же Пар. Следовательно, имеем Дl={1,2,3}, Дr={2,1,3,5} Пример 6: В водоѐме два пескаря, два карася и одна щука. Зная, что карась и щука – хищные рыбы (щука может съесть карася), выяснить бинарное отношение «R – быть съеденным» (т.е. быть пищей) с помощью матрицы. Решение: Т.к. пескарь не является хищной рыбой, он себя не ест, и карасии щуки тоже не едят себя, но щука ест карася, а карась щукуесть не может, то получаем матрицу бинарного отношения.
ПРАКТИЧЕСКИЕ РАБОТЫ Практическая работа №1 «Описание множеств. Геометрическая интерпретация множеств» Запишите множество всех натуральных делителей числа 15 и найти число его элементов. Дано множество . Укажите, какие из чисел 3,4,5,13,25, этому множеству. Дано множество Какие из следующих записей НЕ верны: а) ; в) д) ; б) г) ; е) Задайте множество А = {1, 3, 5, 7, 9} характеристикой его элементов. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7}, S = {4, 6}. Поставьте знаки так, чтобы получились верные утверждения: M…P M…T S…P T…S n(M)…n(T) Задайте числовое множество описанием характеристического свойства его элементов: [-5; 3]. Х – множество млекопитающих, Н = {львы, тигры, волки, лисы}, М = {медведи, волки, орлы, страусы, обезьяны, киты}. Какие из данных множеств являются подмножеством множества Х? Изобразите данные множества с помощью диаграмм Эйлера-Венна. Решение: Множество М не является подмножеством множества Х, т.к. орлы и страусы – птицы, а не млекопитающие: Установите, принадлежат ли множеству В ={х| х=(n2 + 9)/n2, nN} числа: 2, 5, -7? Сформируйте множество В равное множеству А={5√1, 6√4, 7√9, 8√16} Проверьте на равенство множества C={x|x2 -5x+6=0} и D={2} Определите мощности множеств {0}, {п,е,р,п,е,н,д,и,к,у,л,я,р}, {{е},е} Перечислите элементы множества Y= { x|x2 -5x+6=0} Начертите фигуры, изображающие множества: А={(x,y)∈R2 | x2+y2 В={(x,y)∈R2 | x2+(y-1)2 Практическая работа №2 «Операции над множествами» Даны отрезки A=[-4;5] ,B=(2;├ 6], C=(5;├ 10]. Найдите следующие множества и изобразите их кругами Эйлера: а)(A∪B)∪C; в)A∩B; д)(C∪B)\(A∩B) Даны множества A и B: A = {X| xR, X 2}, B = {X| xR, -5 ≤ X ≤ 8} Изобразите результат каждой операции на координатной прямой (плоскости): а) AB; б) A B; в) A \ B; г) B \ A; д) ¬А; е) ¬В; ж) A´ B з)B’ А Даны множества: А={(x,y)∈R2 | x2+y2 В={(x,y)∈R2 | x2+(y-1)2 Какие фигуры изображают множества АUВ, А∩В, R2\А? На диаграммах Эйлера-Венна изобразить результат операций: Пусть U – универсальное множество всех компьютеров в фирме. А – множество всех компьютеров, проработавших больше 2 лет; В – множество всех компьютеров, имеющих процессор Pentium-4; C – множество всех компьютеров, имеющих модем. Каков содержательный смысл каждого из следующих множеств: а) ¬(АВ) б) (А\В)\С в) ¬А (С\В) г) А\С д) АВ Пусть U – универсальное множество всех книг в мире; А – множество книг, имеющихся в библиотеке КамАЗа; В – множество книг о компьютерах; С – множество книг на иностранных языках; D - множество книг издательства «Наука»; E - множество книг в твердом переплете. Каков содержательный смысл следующих множеств: а) А В С б) ¬В \ ¬С в) АВ А г) ¬(¬D) д) Е D В хлебопекарне испекли 300 пирожков. Среди них всего с мясом 116, с рисом 94 пирожка. Только с капустой 30, только с мясом 58, только с рисом 42, только с капустой и рисом 20, количество пирожков с капустой и с мясом равно количеству пирожков с рисом и мясом. Сколько пирожков со всеми тремя начинками сразу, сколько всего с капустой, сколько без начинки. Упростите выражения: - (ABCD’)(CA’)(B’C) (CD); - (A\B) (A\C) - (AB)(AB) Докажите, что: - (AB)’=A’B’; - A(AB)=A; - (AB) (CD)=(AC) ( BC) (AD) ( B D); - (AB)\(AC)= (AB)\C; - A\ (BC)= (A\B) (A\C) Даны результаты операций, проведенных над множествами E,F,H. Определить из каких элементов состоят эти множества. 1) EF H ={e, f , g, h, m}; 2) F \ H = {g, m} ; 3) E \ F = {e}; 4) H E ={e, f ,h}; 5) E F ={ f , g, h}. Пусть универсальное множество U – все преподаватели кафедры «Прикладной математики и управления»; А - множество всех преподавателей старше 25 лет; В - множество всех преподавателей, имеющих высшее образование; С - множество всех программистов; D - множество всех преподавателей, знающих английский язык. Сопоставьте следующие множества и соответствующие им характеристические свойства: а) множество всех преподавателей не старше 25 лет и множество всех программистов с высшим образованием; б) множество всех преподавателей с высшим образованием и в возрасте старше25 лет, но не являющихся программистами; в) множество всех программистов не знающих английского языка; г) множество всех программистов без высшего образования и не старше 25 лет; д) множество всех преподавателей младше 25 лет и множество всех преподавателей, не работающих программистами; е) множество всех программистов младше25 лет AB ¬C 2)C \ B \ A 3)¬A (B C) 4)С\D 5 ) ¬A ¬C 6) ¬DВ 7)С \ ¬(¬A) 2.3. Практическая работа «Отношения и операции над ними» Пусть М={1,2,3,4,5,6,7}. Составить матрицы отношений R1,R2, R3M2, если R1 — «быть остатком от деления на 3», R2 –«в сумме давать 9», R3 – «произведение должно быть больше 7» Пусть М={1,2,3,4,5,6,7,8,9}. Составить матрицу отношения R1, R2 M2, если R1 - «быть наибольшим простым множителем для четных чисел» (нельзя делить число на само себя и единиц). R2 - «быть наименьшим простым множителем для нечетных чисел» (нельзя делить число на само себя). Составить матрицу отношений, заданных на системе множеств (F), где F={ 1,2,3,4 }; R – «пересекаться с …». (F)={ {}, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4},{1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4} }. Пусть М={1,2,3,4,5,6,7}. Составить матрицу отношения R, если: R={(a,в) : (a+в) – нечетное} Пусть А – алфавит (множество всех букв в русском алфавите). Задано множество М={а, б, в ,г, д, е, и ,к, л}– подмножество множества А. Задать матрицей следующее отношение: R= {(х,у) : х- согласная, у – гласная} По данным отношениям R1, R2, R3, R4 составить структуру множества элементов. Если R1 – «быть родными братьями», R2 – «быть дедом…», R3 – «быть дядей…», R4 – быть прадедом…». R1={ (b,c), (e,f), (h,k) }. R2={ (a,d), (c,g), (f,h), (f,k), (a,f), (a,e) }. R3={ (c,d), (b,e), (b,f), (e,g) }. R4={ (a,g), (c,h), (c,k) }. Найти декартовое произведение множеств А и В, если А={а,b,d }, B={ f,d,e}. Выписать все элементы декартового произведения множество АхВхС, если: А={1,2}, B={a,b,c}, C={k,l,m}. Изобразите на декартовой плоскости множество 0;1) (0,1); 0;10;1); 0; 1) R; N R; N 1;2;1;2 N; 5;6;9 R. Постройте множество А2,если: A={0,1}; A={x,y,z}; A={0,2,4,6,8}; A={1,3,5,7}; A={день,ночь}; A={a,b,c,d} КРИТЕРИИ ОЦЕНКИ ПРАКТИЧЕСКИХ РАБОТ
Список использованных источников Основные источники: Спирина М.С., Дискретная математика. учебник для СПО ОИЦ «Академия», 2010. 368 с. Карпова И.В. Занимательная дискретная математика Дополнительные источники: 1. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. — М.: Наука, 2007. 408с. 2. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: учеб. пособ. 1. М.: Форум: ИНФРА М, 2007. 3. Кольман Э. Зих О. Занимательная логика. М.: Наука, 2008. 127с. 4. Просветов Г.И. Дискретная математика: задачи и решения. Учебно-практическое пособие /– М.: Альфа-Пресс, 2009. 136 с. 5. Шишмарев Ю.Е., Емцева Е.Д., Солодухин К.С. Дискретная математика: Сборник задач. Ч.1. – Владивосток: ВГУЭС, 2000. 98с. |
